I. 서 론
II. 빔형성기법
2.1 일반빔형성(Conventional Beamforming)
2.2 적응 빔형성(Adaptive Beamforming)
2.3 압축센싱(Compressive Sensing)
III. 실 험
3.1 모의실험 결과 분석
3.2 실제 실험 설정 및 결과 분석
IV. 결 론
I. 서 론
해상에서 표적의 위치를 찾기 위해서는 우선적으로 빔형성을 통해 표적의 도래각을 추정한다. 표적이 원거리에 존재할 경우, 표적신호는 평면파로 가정할 수 있으며, 선형 배열 센서에 발생하는 시간지연을 활용하여 표적의 도래각을 추정한다. 빔형성의 주요 문제는 한정된 센서 개수와 낮은 신호 대 잡음비(Signal to Noise Ratio, SNR) 상황에서 좋은 분해능과 강인성을 확보하는 것이며, 이를 해결하기 위해 다양한 방식의 빔형성 기법들이 제안되었다.
가장 먼저 제안된 기법은 일반빔형성(Conventional BeamForming, CBF)으로 센서 배열에 입사된 음장과 전 방향의 조향벡터들의 상관을 통해 출력값을 얻는다. 도래각 추정 기법들 중 가장 단순하면서도 높은 강인성을 갖지만 센서 개수와 배열의 길이가 충분하지 않을 경우 낮은 분해능 결과를 보이는 한계점이 있다.[1]
한정된 센서 배열로부터 발생하는 일반빔형성의 한계점을 극복하기 위해 공분산 행렬의 고유값 분해를 이용하는 Minimum Variance Distortionless Response (MVDR)[2,3]그리고 Multiple Signal Classification(MUSIC)[4] 등과 같은 적응 빔형성 기법들이 제안되었다. 그러나 상관도가 높은 신호가 존재하거나 측정 신호의 수가 부족할 경우 공분산행렬의 고유값 특성을 제대로 활용할 수 없어 빔형성 성능이 저하된다는 한계점이 존재한다.[5,6,7,8]
이러한 적응 빔형성 기법들의 한계점을 극복하기 위해 소수의 의미 있는 값들의 선형결합으로 표현 가능한 희소 신호를 적은양의 측정으로도 복원할 수 있는 압축센싱(Compressive Sensing, CS)이 제안되었다.[9] 압축센싱은 신호를 복원하는 과정에서 의미 있는 값을 제외한 다른 값들이 0이 되어 고해상도의 결과를 획득할 수 있다.
압축센싱은 영상처리와 신호처리 분야에서 활발한 연구가 진행 중이며,[10,11,12] 특히 수중 음향 분야에는 빔형성, 정합장처리 그리고 해양인자 역산 등에 압축센싱을 적용하기 위한 연구가 진행 되고 있다.[13,14,15,16,17,18,19]
압축센싱은 -norm 최소화 문제를 통해 희소신호를 구한다. 그러나 이는 현실적으로 계산량이 많아 적용하기 어렵기 때문에 -norm을 -norm으로 완화하여 희소신호를 복원한다.[9,20,21] 또한, 기존의 압축센싱에서 발생하는 기저불일치 현상을 극복하기 위해 최근 무격자 압축센싱(grid-free compressive sensing)이 제안되었고, 이는 도래각 추정을 위한 연구에 적용되고 있다.[22,23,24,25,26,27]
본 논문에서는 위에서 언급한 기법들의 이론적 배경 및 한계점을 소개하고 모의실험 데이터 및 실제실험 데이터를 통해 각 기법들의 성능을 비교한다. 본 논문의 구성을 다음과 같다. 2장에서는 앞서 언급한 빔형성 기법들에 대한 이론적 배경 및 가정을 소개하고, 3장에서는 모의실험 및 실제실험을 통한 각 기법들의 성능을 비교 및 분석하며 4장에서 결론을 맺는다. 본 논문에서 는 스칼라, 는 벡터 그리고 는 행렬을 의미한다.
II. 빔형성기법
2.1 일반빔형성(Conventional Beamforming)
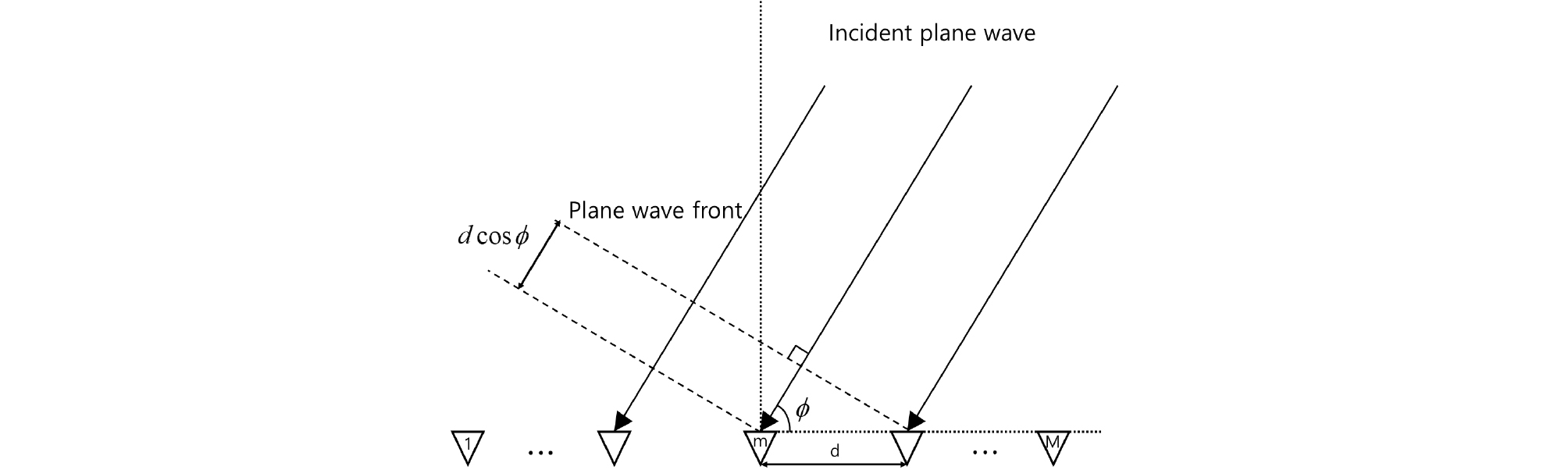
일반빔형성은 개의 센서 배열로부터 얻은 관측 신호 를 조향벡터 와의 상관을 통해 출력값을 산출하며, 이는 Eq. (1)과 같다(Fig. 1 참고).
| $$P=\left|\overrightarrow y^H\overrightarrow a(\phi)\right|^2=\overrightarrow a(\phi)^H\overrightarrow y\overrightarrow y^H\overrightarrow a(\phi),$$ | (1) |
여기서 의 번째 성분 은이다.
이때, 스냅샷 혹은 측정개수가 개라면 신호를 Eq. (2)와 같이 공분산행렬()로 만들 수 있으며 이를 Eq. (1)에 적용하여 일반빔형성의 출력값을 Eq. (3)과 같이 표현할 수 있다.
| $${\hat{R}} = \frac{1} {L} \sum _{l=1} ^{L} {\vec{y}} _{l} {\vec{y}} _{l}^{H}.$$ | (2) |
| $$P_{CBF}(\phi)=\overrightarrow a(\phi)^H\widehat R\overrightarrow a(\phi).$$ | (3) |
일반빔형성은 센서 배열에 수신된 신호를 여러 방향의 조향벡터와 단순 상관시켜 결과를 얻으므로 잡음에 강인하며 측정개수의 제약을 받지 않는다는 장점이 있지만 센서 배열의 길이가 제한된 경우 근접한 조향벡터들의 상호 상관도가 높아 낮은 분해능을 갖는다는 한계가 있다.
2.2 적응 빔형성(Adaptive Beamforming)
본 절에서는 센서 배열의 길이가 제한된 경우에도 높은 해상도를 얻을 수 있는 적응빔형성 기법들 중 대표적인 기법인 MVDR과 MUSIC에 대한 이론적 배경 및 각 기법들이 가진 한계점에 대해 소개한다.
2.2.1 Minimum Variance Distortionless Response (MVDR)
MVDR은 일반빔형성의 해상도를 개선하기 위한 대표적인 적응빔형성 기법으로 신호 대 잡음비를 최대화함으로써, 신호 를 간섭신호를 포함한 잡음 과 구분하여 고해상도의 빔형성 결과를 획득한다.[1]
신호 가 각도로 센서 배열에 수신된다고 가정하자. 이 때, 는 조향벡터를 이용하여 로 표현할 수 있다. 정확한 신호의 도래각 추정을 위해 SNR을 최대화하는 를 구하고자 하며, 이는 Eq. (4)와 같이 기술된다.
여기서 는 신호의 크기와 연관된다.
그러나 실제로 잡음공분산행렬 을 분리해 사용할 수 없기 때문에 잡음이 포함된 다중 관측 측정으로 구한 Eq. (2)의 공분산 행렬 을 이용하여 를 구한다. 신호 대 잡음비를 최대화하는 최적의 은 라그랑주 승수법(Lagrange Multiplier)전개를 통해 최적화 문제[Eq. (5)]의 해를 도출함으로써 구해지는데, 이는 Eq. (6)과 같다.[6]
| $$\min\overset{\mathit\rightarrow}{\mathit w}^{\mathit H}\widehat R\overrightarrow{w\;\;}\mathrm{subject}\;\mathrm{to}\;\overrightarrow w^H\overrightarrow a(\phi_0)=1.$$ | (5) |
| $${\overrightarrow w}_{MVDR}=\frac{\widehat R^{-1}\overrightarrow a(\phi_0)}{\overrightarrow a(\phi_0)^H\widehat R^{-1}\overrightarrow a(\phi_0)}.$$ | (6) |
이를 이용한 빔형성 출력값 은 Eq. (7)와 같다.
| $$P_{MVDR}(\phi)=\lbrack\overrightarrow a(\phi)^H\widehat R^{-1}\overrightarrow a(\phi)\rbrack^{-1}.$$ | (7) |
이와 같이 다중 추정으로부터 얻은 공분산행렬을 사용하여 MVDR의 결과를 얻는 방법을 Sample Matrix Inversion(SMI)이라 한다.[3]
만약 수신신호가 간섭신호와 상관성이 없다면 Eq. (6)은 공분산행렬의 역행렬정리를 통해 Eq. (8)과 같이 표현할 수 있다.[6]
| $${\overrightarrow w}_{MVDR}=\beta R_n^{-1}\overrightarrow a(\phi_0),$$ | (8) |
상수 는 , 는 특정 기준에 따라 값이 결정되는 스칼라 비례상수로 이 되도록 적절히 선택되며 는 잡음 신호의 크기와 연관된다.
은 간섭신호에 해당하는 고유값인 와 잡음에 해당하는 고유값 으로 나타낼 수 있으며 간섭신호의 고유값은 잡음의 고유값보다 크므로() , 은 Eq. (9)과 같이 근사된다.
여기서 이며 는 고유벡터이다.
간섭신호의 조향벡터 는 처음 개의 고유벡터 의 선형결합으로 표현되므로, 잡음에 해당하는 나머지 고유벡터 와 직교한다. 따라서 간섭신호는 직교성에 의해 Eq. (10)과 같이 제거된다.
| $$\overrightarrow w_{MVDR}^H\overrightarrow a(\phi_j)\cong\;\frac\beta{\sigma^2}\sum_{i=K}^P\rho_i\overrightarrow e_i^H\overrightarrow a(\phi_j)=0,\;\;j=1,\;\cdots\;,K-1,$$ | (10) |
측정개수가 충분하다면 MVDR은 백색잡음을 감소시켜 제한된 센서 배열에서 일반빔형성보다 높은 해상도를 얻을 수 있지만, 공분산행렬의 특성을 활용하기 때문에 많은 수의 측정개수를 필요로 한다는 한계점이 있다. 특히, 계산 시 공분산 행렬의 역행렬 역산이 필요한데 이를 위해서 측정개수는 센서 개수 이상이어야 한다(이 때, 잡음은 가우시안 분포를 따른다고 가정한다). 또한, 수신 신호에 간섭이 존재하는 환경에서 이상적인 MVDR의 출력 손실비를 절반 이하로 유지하기 위해 측정개수는 센서 개수의 2배 이상이어야 한다.[5] 여기서 출력 손실비는 이상적인 MVDR에서 얻을 수 있는 신호 대 잡음비와 SMI결과를 통해 얻은 신호 대 잡음비의 비를 의미한다.
MVDR에서 이와 같은 결과를 얻기 위해서 무상관협대역신호가 백색잡음과 함께 선형 배열 센서에 수신된다고 가정한다. 그러나 수신신호와 간섭신호가 상관성이 있는 경우(특히, 해상환경과 같이 한 개의 신호원이 여러 방향으로 들어오는 수중 도파판 효과로 인해 상관도가 높은 신호, 즉 주파수가 동일하지만 위상차가 상이한 신호가 센서 배열에 들어오는 상황에서) MVDR의 성능이 저하된다. 이는 상관 신호에 적절한 위상을 보상함으로 관심신호를 표현할 수 있고, 이로 인해 표적신호 고유값과 간섭신호 고유값 구분이 어렵기 때문이다.[6,7]
2.2.2 Multiple Signal Classification(MUSIC)
MUSIC은 두 개 이상의 무상관 신호가 센서에 수신된다면 공분산행렬이 각 신호들의 고유값으로 이루어지며, 그 크기(, )에 의해 공분산행렬이 Eq. (11)과 같이 잡음부분공간()과 신호부분공간()으로 구별된다는 특징을 이용한다.
| $$R=R_s+R_n=E_s\Gamma_sE_s^H+E_n\Gamma_nE_n^H.$$ | (11) |
또한 공분산행렬의 잡음부분공간은 예상하는 신호와 직교하다는 성질을 이용하여 잡음부분공간과 조향벡터의 상관값의 역수로 Eq. (12)과 같이 빔형성 출력을 얻을 수 있다.[1]
| $$P_{MUSIC}(\phi)=\lbrack\overrightarrow a(\phi)^HE_nE_n^H\overrightarrow a(\phi)\rbrack^{-1}.$$ | (12) |
수신 신호로 구한 공분산 행렬은 Eq. (2)와 같이 평균을 사용한 추정값으로, 샘플수가 적을 경우 공분산 행렬을 정확하게 추정할 수 없고 이는 고유값의 변동을 야기한다. 따라서 MVDR과 마찬가지로 MUSIC 역시 공분산행렬의 부분공간을 분명하게 구분하기 위해 충분한 측정개수가 주어져야 한다.[8]
또한, 공분산행렬이 가질 수 있는 고유값의 최대 개수는 센서 개수와 동일하고, 이는 탐지할 수 있는 표적신호의 최대 개수와 동일하다. 이에 따라 MUSIC은 표적개수가 배열 센서의 개수보다 적어야 한다는 한계점을 가진다.[4]
2.3 압축센싱(Compressive Sensing)
압축센싱은 신호의 희소성(sparsity)를 가정한 뒤 최적화 문제를 통해 답을 구해내는 기법으로 신호가 희소한 경우 나이퀴스트 새넌 샘플링 이론보다 훨씬 적은양의 샘플로도 원 신호를 완벽하게 재구성 할 수 있음을 입증하였다.[9] 특히, 해상표적신호의 경우 관측 가능한 범위 내에서 표적의 수는 소수이기 때문에 수신 신호를 희소성을 가지는 신호로 간주할 수 있어 압축센싱 기법을 적용한 도래각 추정이 가능하다.
본 절에서는 일반적인 압축 빔형성 기법의 이론적 배경 및 한계점을 소개하고 압축 빔형성이 가지고 있는 기저 불일치 문제를 극복할 수 있는 무격자 압축 빔형성에 관해 소개한다.
2.3.1 압축 빔형성(Compressive Beamforming)
잡음을 포함한 관측신호 와 표적신호 간의 선형관계식은 Eq. (13)와 같이 표현된다.
| $$\overrightarrow y=A\overrightarrow x+\overrightarrow n,$$ | (13) |
여기서 행렬 는 센싱 행렬이며, 이를 구성하고 있는 는 방향의 조향벡터, 은 잡음이다.
압축센싱 모델에서 표적신호 의 차원 은 관측 신호 의 차원 보다 훨씬 크므로(), Eq. (13)은 과소결정 시스템 문제가 된다. 압축센싱은 이러한 선형 문제를 해결하기 위해 신호의 희소성을 이용하여, Eq. (14)과 같이 -norm 최소화문제를 통해 최적해를 도출한다.
| $$\min\;{\left\|\overrightarrow x\right\|}_0\;\;\mathrm{subject}\;\mathrm{to}\;\overrightarrow y=A\overrightarrow x.$$ | (14) |
Eq. (14) 문제의 해를 도출함으로써 고해상도의 빔형성 결과를 얻을 수 있지만 -norm 최소화 문제는 해를 구하기 위한 계산량이 너무 높다는 단점이 있다. 이에 센싱 행렬의 열간 상관값이 일정 조건을 만족할 때 -norm 최소화 문제가 -norm 최소화문제와 동치임을 이용하여, Eq. (15)과 같이 완화하여 해를 구한다.[20]
| $$\min\;{\left\|\overrightarrow x\right\|}_1\;\;\mathrm{subject}\;\mathrm{to}\;\overrightarrow y=A\overrightarrow x.$$ | (15) |
-norm 문제는 컨벡스 문제이므로 -norm 문제에 비해 계산이 용이하다.
2.3.2 압축 빔형성의 한계
압축 빔형성은 의미 있는 값 이외에는 0을 가지는 답을 구하므로 일반빔형성에 비해 고해상도의 결과를 얻을 수 있으며, 공분산행렬의 고유 값 특성을 이용하지 않고 관측신호를 형성한 희소신호를 구하기 때문에 상관신호 유무에 제약이 없다.[12] 그러나 일반적인 압축 빔형성은 이산 영역에서 표적 도래각을 추정하기 때문에 발생하는 기저불일치에 의해 그 성능이 저하된다는 한계점이 존재한다.[22,23]
이러한 한계점을 극복하기 위해서는 표적신호가 센싱 행렬 에 포함되도록 해야 하므로, 센싱 행렬을 구성하는 조향벡터 도래각 간격을 충분히 좁게 설정해야한다. 그러나 센싱 행렬의 조향벡터 도래각 간격을 너무 좁히면 벡터 간 상관도가 증가하여 Eq. (15)를 이용하여 답을 구하기 어려워지므로, 정확한 답을 구하기 위해서는 이전의 기법들과 마찬가지로 좁은 간격의 많은 센서 수가 필요하다.[12] 이러한 제한된 센서 개수에서 기저불일치 문제를 해결하기 위해 무격자 압축 빔형성이 제안되었다.[24,25,26,27]
2.3.3 무격자 압축 빔형성
무격자 압축 빔형성은 센싱 행렬로부터 미리 정해진 조향벡터의 선형결합을 찾아내는 것이 아닌 atomic norm과 쌍대성을 이용하여 연속 도래각 영역에서 표적의 도래각을 추정하는 방식으로 기존 압축 빔형성에서 발생하는 기저불일치 문제를 해결한다.
m번째 센서에 수신되는 음압은 연속 정현파 스펙트럼 영역에서 희소한 신호가 있는 모든 방향의 평면파 중첩으로 Eq. (16)과 같이 표현되며, 관측신호 는 Eq. (17)과 같이 표현할 수 있다.
| $$y_m=\sum_{i=1}^Kx_ie^{jkdm\cos\phi_i}.$$ | (16) |
| $$\overrightarrow y=F_Mx,$$ | (17) |
여기서 은 찾고자 하는 수신신호 를 관측신호 에 선형 변환하는 행렬로써, 행렬의 열은 , 로 구성되며 이 때, 는 희소신호의 개수이다.
Atomic norm의 정의는 Eq. (18)와 같으며, 연속 영역에서 이산 영역에서의 -norm에 대응하는 값으로 간주 할 수 있다.[22]
| $$\parallel x\parallel_A=\sum_{i=1}^K\vert x_i\vert.$$ | (18) |
-norm대신 atomic norm을 사용한 희소신호 복원 식은 Eq. (19)와 같이 표현할 수 있다(는 연속공간에 존재하고 이는 이전의 이산 표적신호와 구별되므로 벡터로 표기되지 않는다).
| $$\min\parallel x\parallel_A\;\;\;\mathrm{subject}\;\mathrm{to}\;\overrightarrow y=F_Mx,$$ | (19) |
는 연속 도래각 영역에 존재하는 에 의해 연속 공간에 존재하기 때문에, Eq. (19)는 무한차원 문제가 되어 최적화 해를 도출할 수 없다. 따라서 쌍대성을 활용하여 최적화 해를 도출한다.[24,28] Eq. (19)를 쌍대성 문제 형태로 변환하기 위해서는 Eq. (20)과 같이 라그랑주를 사용한다.
| $$L(x,\overrightarrow c)=\vert\vert x\vert\vert_A+Re\lbrack\overrightarrow c^H(\overrightarrow y-F_Mx)\rbrack,$$ | (20) |
여기서 는 쌍대변수의 벡터이다. 쌍대함수 는 라그랑주의 하한으로 Eq. (21)과 표현할 수 있으며 쌍대 함수 는 Eq. (22)와 같이 표현할 수 있다. 또한 쌍대 함수를 최대화함으로써 Eq. (23)을 유도 할 수 있다.[23,24]
| $$\max Re\lbrack\overrightarrow c^H\;\overrightarrow y\rbrack\;\;\;\mathrm{subject}\;\mathrm{to}\parallel F_M\overrightarrow c\parallel_\infty\leq1,\;\overrightarrow c\in C^M.$$ | (23) |
쌍대성을 이용하면 최소화 문제 Eq. (19)는 Eq. (23)과 같은 최대화 문제로 바뀌게 되는데, 이 때 Slator’s condition을 만족하면, 두 문제의 해는 정확히 일치한다.[28] Atomic norm 최소화 문제는 컨벡스 문제임과 동시에 선형 등식 제약을 가지므로 Slator’s condition을 만족하며, 쌍대성을 사용하여 전개한 최대화 문제는 본래 문제인 Eq. (19)과 동일한 문제로 귀결되고 최적화 해를 구하기 위해 아래와 같은 준정부호 프로그래밍(SemiDefinite Programming, SDP)을 사용한다.
Eq. (23)을 SDP로 유도하는 과정에서 행렬 가 정의되며, 이 때 는 Eq. (24)의 조건을 만족한다. Eq. (24)의 SDP 제약조건에서 슈어(Schur) 보수를 이용하여 전개하면 이 되며, 이를 양의 준정부호 정의에 따라 임의의 벡터 를 적용하면 가 된다. 이 때, 를 만족하는 가 주어지면 을 만족하므로 쌍대성 문제 Eq. (23)이 SDP 문제 Eq. (24)와 동일한 문제로 귀결된다.[28]
Eq. (13)와 같이 잡음이 포함된 경우, Eq. (23)은 준정부호 프로그래밍 Eq. (25)와 같이 수정된다.
여기서 는 정규화 변수(regularization parameter)이다. Eq. (25)의 최적화 해를 풀어내면 쌍대변수(dual variable)인 값을 구할 수 있다.[24,29]
그러나 쌍대문제는 최적의 쌍대변수 값을 제공하는 것으로 원 문제의 해를 제공하지는 않는다. 따라서 Eq. (25)의 제약조건의 등식을 만족하는 값을 찾음으로써 연속영역에서 표적신호의 도래각 를 추정하고, 이를 Eq. (26)을 통해 도래각의 해당하는 표적신호 값을 도출한다.
| $${\widehat x}_{CS\;dual}=A_g^+\overrightarrow y,\;\;\overrightarrow a(g_i)=e^{jkd\lbrack1,...,M\rbrack^Tg_i},\;\;g_i\in\widehat G,$$ | (26) |
여기서 는 의 의사역행렬이며 은 primal solution의 support이다.
이를 통해 신호의 진폭을 얻을 수 있으며 기존의 압축 빔형성에서 발생하던 기저불일치 문제를 극복할 수 있다.[24]
III. 실 험
본 장에서는 앞서 설명한 일반 빔형성, 적응 빔형성(MVDR, MUSIC) 그리고 무격자 압축 빔형성의 성능을 모의실험 및 실제실험을 통해 비교 및 분석한다.
3.1 모의실험 결과 분석
모의실험은 각 기법들의 해상도와 상관신호에 따른 각 기법들의 성능을 비교하기 위해 단일 신호(0°), 2개의 무상관신호(0°, 15°) 그리고 2개의 상관신호(0°, 15°)가 존재하는 환경, 총 3가지 경우에 대해 수행하였으며 신호 대 잡음비는 상대적으로 높은 20 dB로 설정하였다.
모의실험의 송신 신호는 800 Hz의 연속파(Continuous Wave, CW)를 사용하였고, 음속은 340 m/s로 공기 중 음속으로 설정하였다. 음파는 선배열을 통해 수신되는데 이 때 선배열은 8개의 센서로 구성되며, 그 간격은 0.1 m로 공간 앨리어싱이 발생하지 않도록 하며, 이 후 언급될 실제 실험환경과 유사하게 설정하였다.
무격자 압축 빔형성은 특정 시간에서의 단일 측정을 사용한 반면, 그 외의 빔형성기법들은 16개의 다중측정을 사용하였다. 특히, 적응 빔형성 기법들은 공분산 행렬의 고유값 특성을 이용하기 위해 다중측정이 필수적이다.
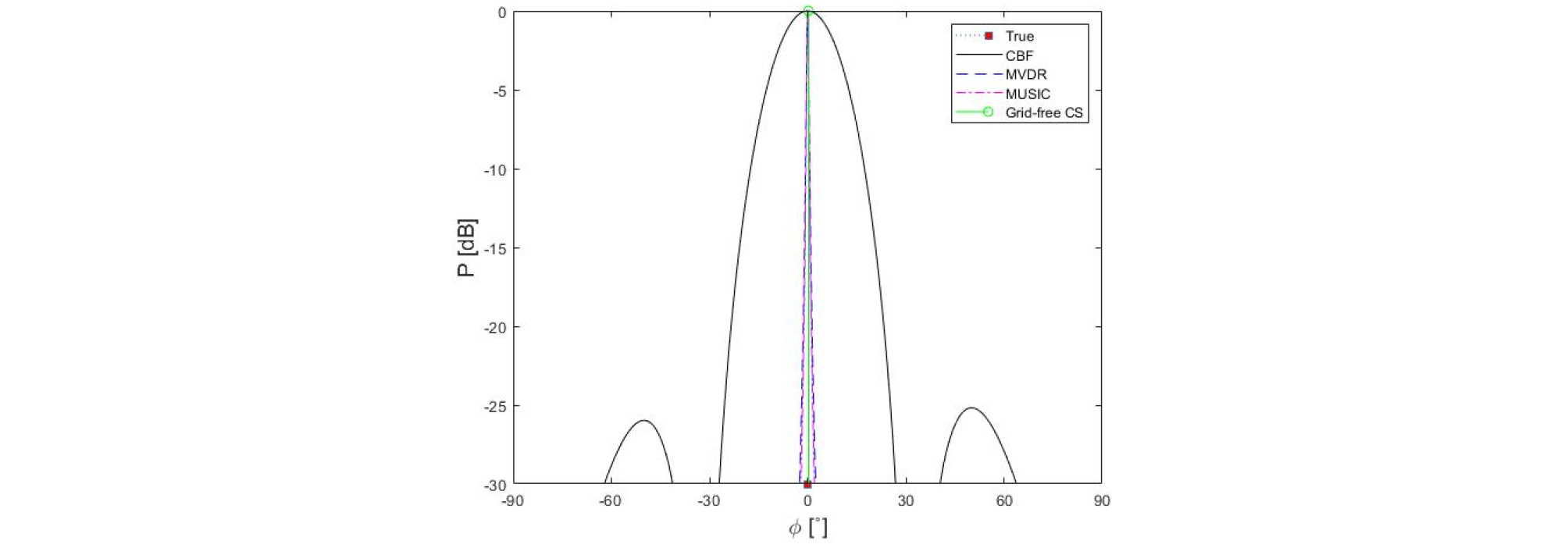
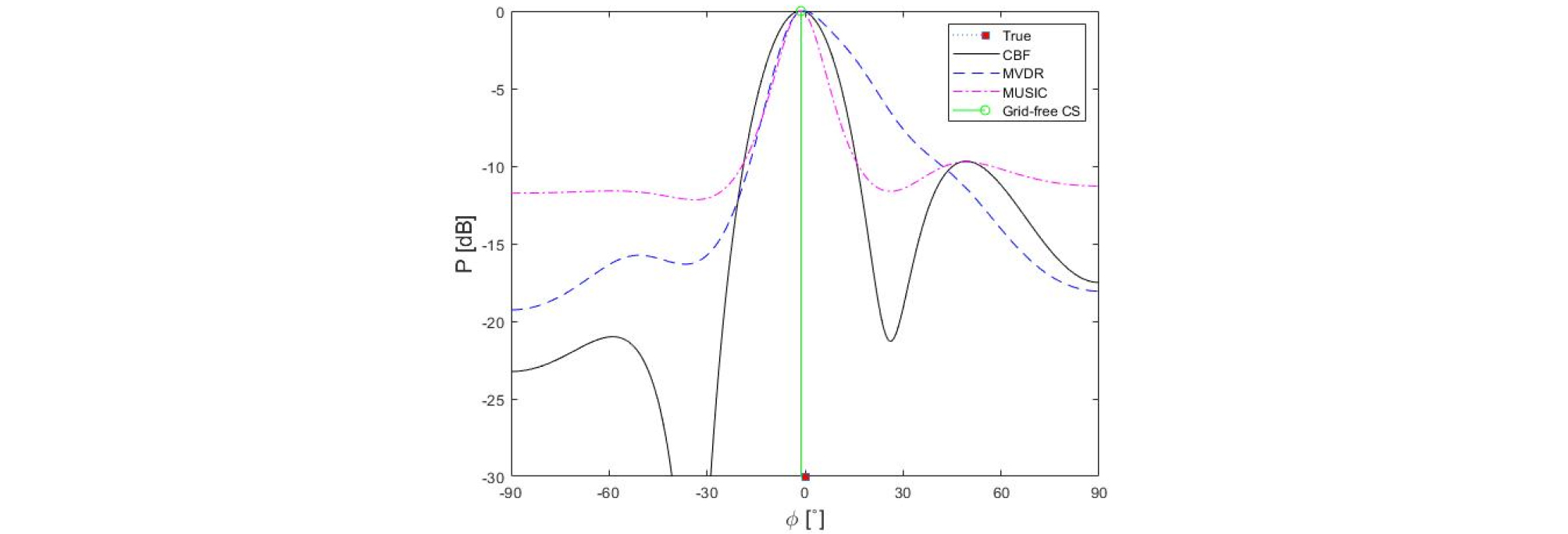
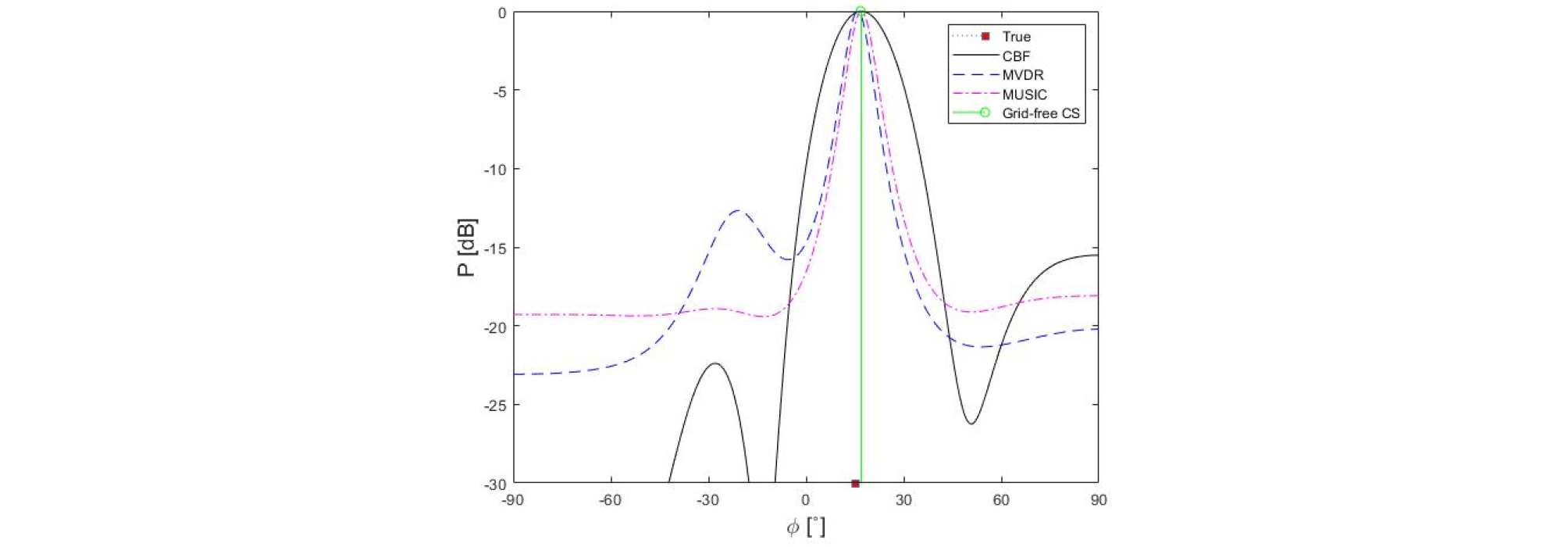
단일 신호만 있는 경우 앞서 언급한 모든 빔형성 기법들이 표적 신호의 도래각을 정확하게 추정함을 Fig. 2에서 알 수 있으며 앞 장에서 언급한 바와 같이 일반 빔형성의 경우 다른 기법들에 비해 낮은 해상도를 보임을 알 수 있다. 이와 같이 제한된 선배열 센서의 경우 빔형성 결과의 해상도를 높이기 위해 고도화된 빔형성 기법을 활용할 수 있다.
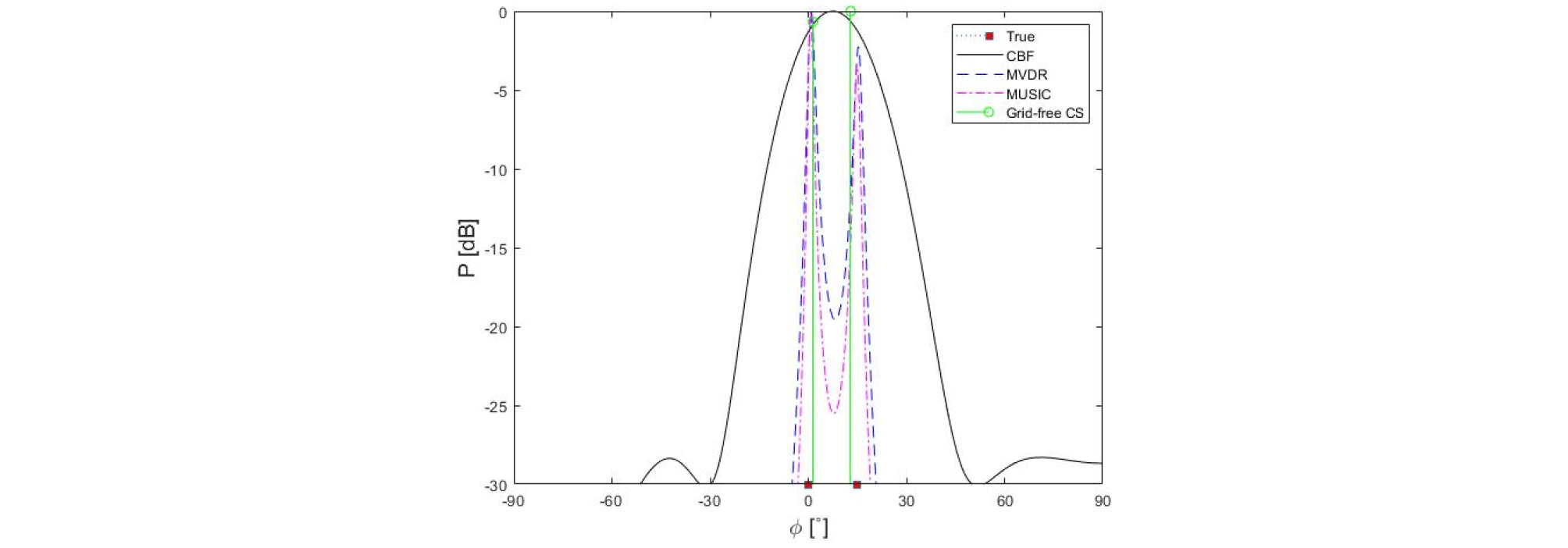
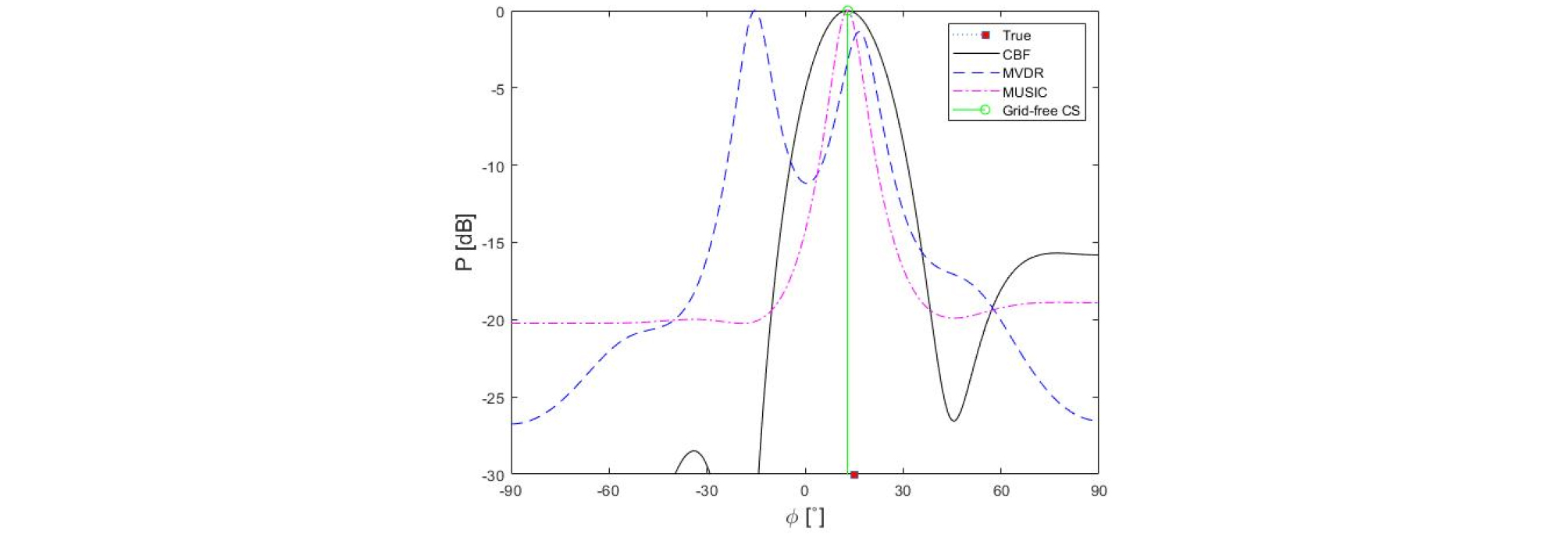
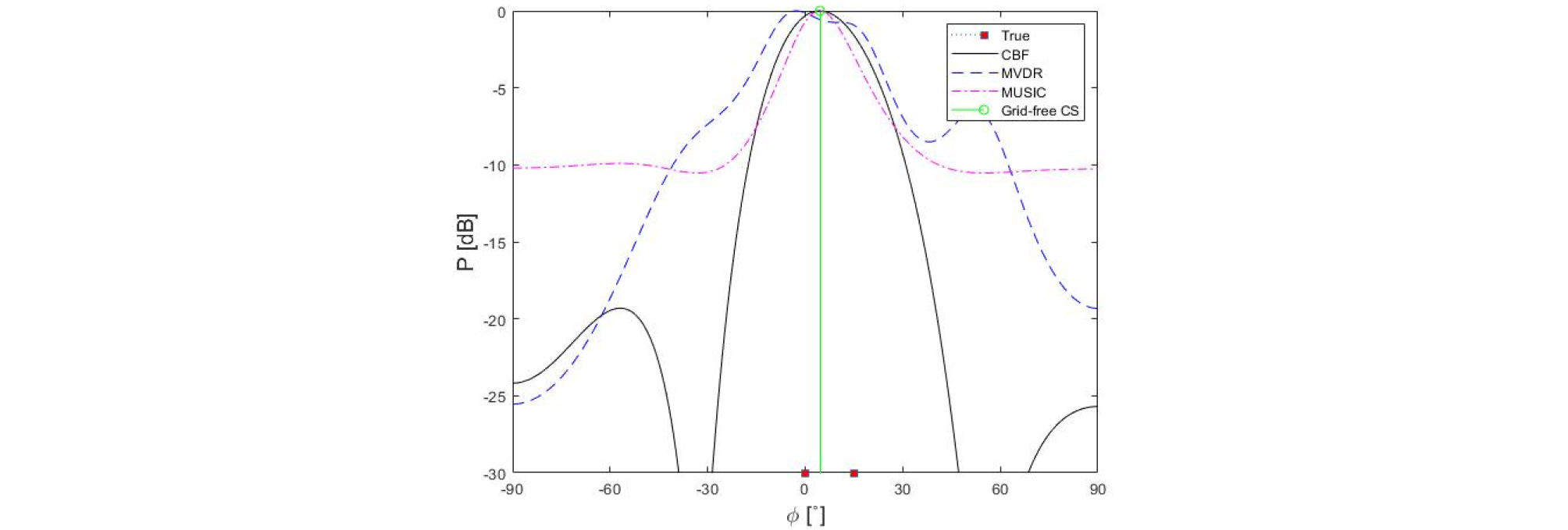
신호 대 잡음비가 동일한 2개의 무상관신호가 존재하는 환경에서 Fig. 3에서와 같이 MVDR과 MUSIC 그리고 무격자 압축 빔형성 기법의 경우 2개의 신호가 구분 가능하나 일반 빔형성의 경우 형성된 두 개의 저해상도 빔의 중첩으로 인해, 음원의 위치와 다른 각도에서 최대값이 나타남을 알 수 있다. 이는 일반 빔형성의 0° 기준 3 dB 빔폭이 47°로[Eq. (27)], 이로 인해 빔폭내에 존재하는 15° 신호 구분이 어렵기 때문이다. Eq. (27)에 보이는 것과 같이 일반빔형성의 해상도를 높이기 위해서는 더 많은 센서의 개수가 필요하다.
| $$\Delta\phi_{3dB}=\sin^{-1}\left[\sin\phi+\frac{0.44c}{Mfd}\right]-\sin^{-1}\left[\sin\phi-\frac{0.44c}{Mfd}\right].$$ | (27) |
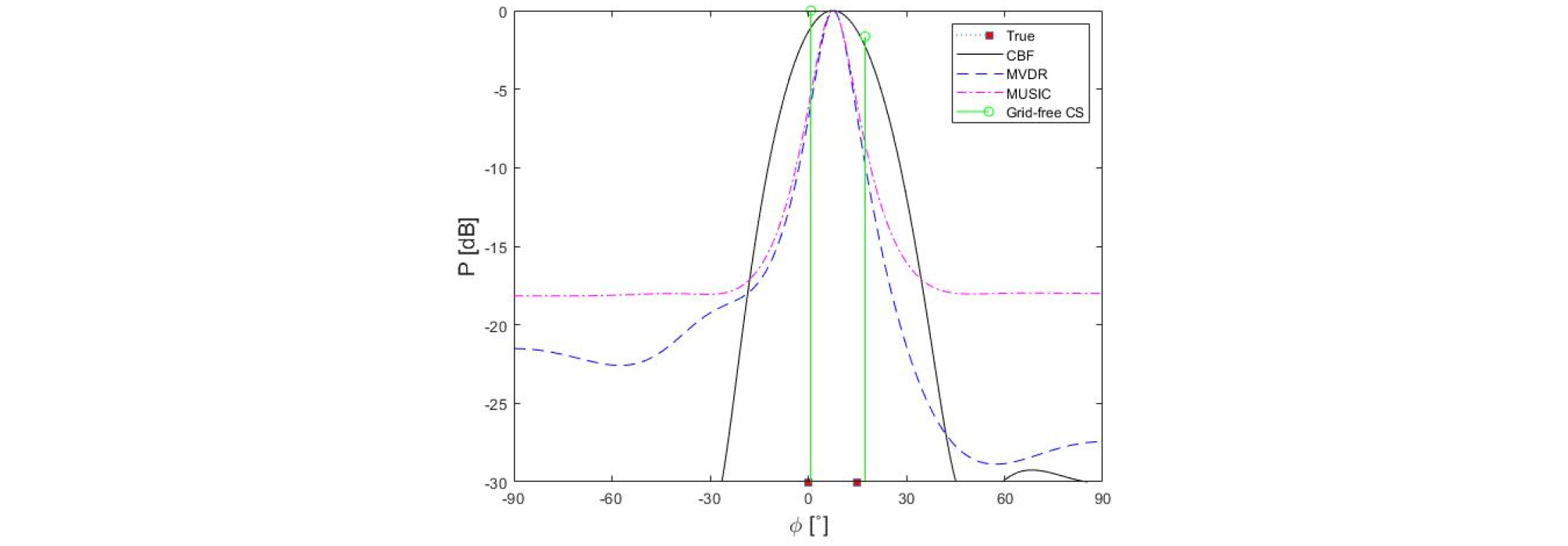
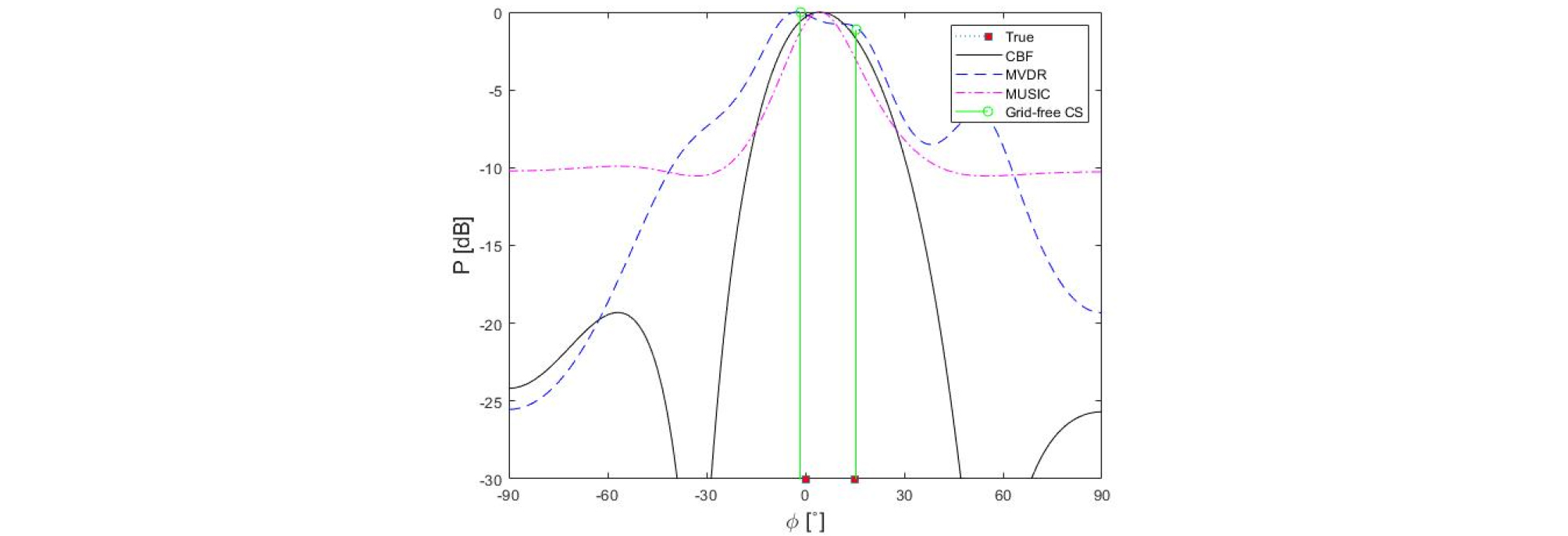
마지막으로 2개의 상관신호가 존재하는 환경에서는 앞장에서 언급한 바와 같이 공분산행렬의 고유값이 상관신호에 영향을 받아 심각한 성능 저하가 발생하는 것을 Fig. 4에서와 같이 알 수 있다. 이는 상관신호의 경우 수신신호부분과 잡음부분 고유벡터들의 상관성으로 인해 두 신호를 구별하지 못하기 때문이다. 반면, 무격자 압축 빔형성은 2개의 무상관신호가 존재하는 환경과 마찬가지로 두 개 신호의 도래각을 구분하는 것을 알 수 있다.
3.2 실제 실험 설정 및 결과 분석
본 절에서는 앞선 수행한 모의실험의 결과가 실제 실험에서도 동일한 결과를 보여주는지 실제 실험을 통해 확인한다. 실제 실험은 단일신호가 수신되는 환경 그리고 2개의 신호가 수신되는 환경에서 수행하였다.
실험공간은 너비 2.5 m, 폭 10 m 그리고 높이 2.5 m의 밀폐된 공간에서 진행하였으며 모의실험과 마찬가지로 800 Hz의 연속파를 사용하였다. 800 Hz의 신호가 공간상에서 앨리어싱이 발생하는 마이크로폰 간격은 0.2 m 이상이므로 본 실험에서는 앨리어싱이 발생하지 않도록 총 8개의 마이크로폰(모델명 : AUDIOTE CHNICA, 수신주파수범위 : 70 Hz ~ 16000 Hz)를 0.1 m 간격의 선형배열로 설치하였으며 1개 또는 2개의 스피커(모델명 : BZ-U190, 발생주파수범위 : 150 Hz ~ 17000 Hz)를 이용하였다. 또한 마이크로폰 배열의 중점과 스피터 간의 거리를 2 m로 설정하여 원거리 음장 기준을 만족하도록 하였다. 실제 실험은 Reference [30]과 동일한 환경에서 수행하였으며 실제 실험 환경은 Fig. 5와 같다.
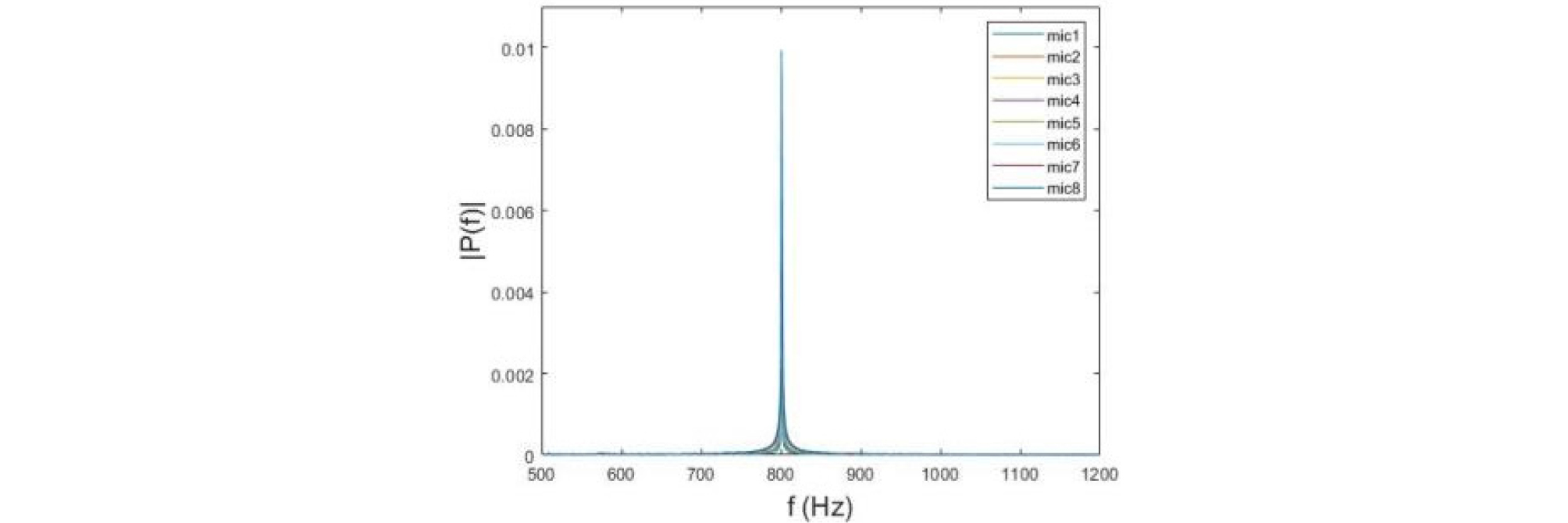
800 Hz의 신호를 연속적으로 방사하는 상태에서 샘플링 주파수를 44.1 kHz로 설정하여 10 s간 측정하였다. 측정값 간의 원활한 전환을 보장하기 위해 각각의 측정값은 50 % 중첩하여 처리하였으며,[1] 각각의 마이크로폰으로 수신된 신호를 고속 푸리에 변환(Fast Fourier Transform, FFT)을 통해 확인한 결과 Fig. 6과 같이 스피커에서 방사한 신호가 마이크로폰으로 정확히 수신됨을 확인하였다.
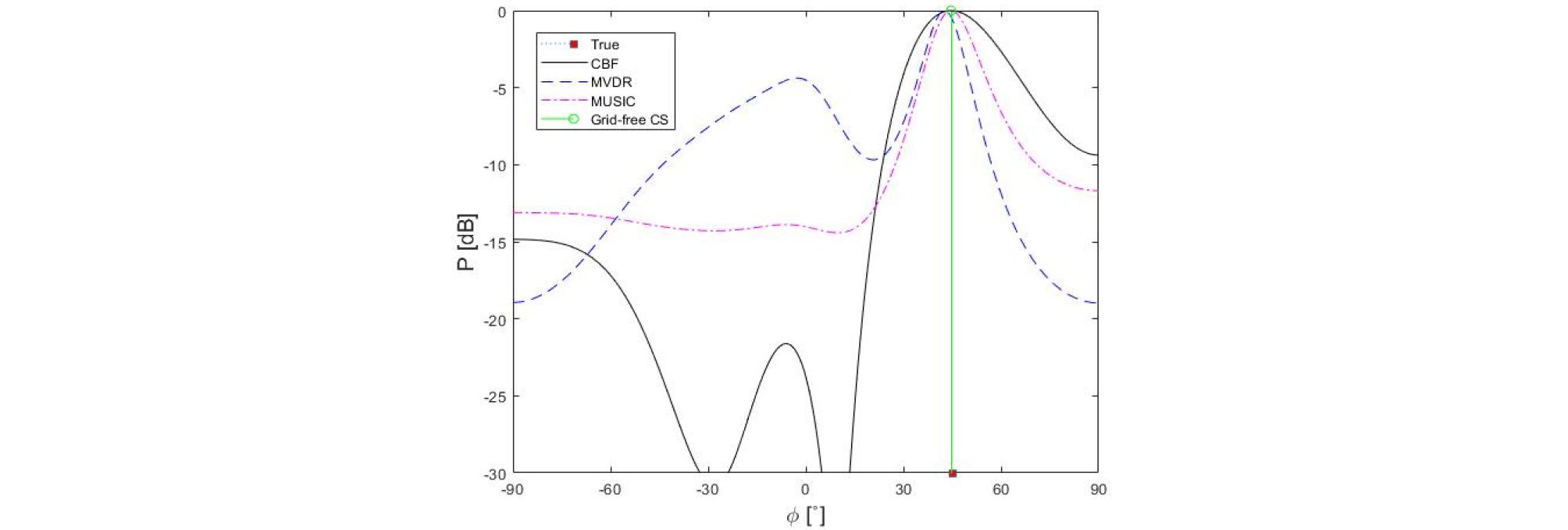
첫 번째 실험은 단일 신호가 수신되는 경우로 0°, 15° 그리고 45°의 입사환경에서 수행되었다. 신호가 마이크로폰 배열 정면 즉, 0°에서 방사되는 경우 모의실험과 마찬가지로 일반 빔형성, 적응빔형성 그리고 무격자 압축 빔형성 모두 최대 1.8°, 15°의 경우 최대 2.4° 그리고 45°의 경우 최대 0.4도의 오차범위 내에서 수신 신호의 도래각을 추정하였음을 알 수 있으며 각각의 빔형성 기법의 결과는 Figs. 7 ~ 9와 같다. 각각의 기법이 도래각을 정확하게 추정하지 못하는 원인은 스피커와 마이크로폰의 높이 차, 방사신호 측정각도 그리고 마이크로폰의 완벽하지 않은 전방향성에 따른 오차로 판단된다.
실제 실험 결과 일반빔형성과 무격자 압축 빔형성의 경우 모의실험과 유사한 결과를 보여주었지만 Figs. 8과 9에서 볼 수 있듯이 적응 빔형성 기법인 MVDR과 MUSIC 모두 빔폭 증가 현상이 나타났으며 특히, MVDR의 경우 실제 도래각 외에 또 다른 피크점이 형상됨을 알 수 있다.
이러한 결과는 모의실험과 다르게 실제 실험의 경우 밀폐된 실험 공간에서 발생하는 반사 신호가 원인이라고 판단하였으며 이러한 결과를 분석하기 위해 실제 실험에서 발생하는 반사 신호의 각도들을 예측하여(-35°, 30°, 70°) 모의실험을 수행하였다. 표적신호와 반사 신호의 신호 대 잡음비는 센서에 들어오는 소음 준위를 기준으로 각각 15 dB, -5 dB, 10 dB 그리고 5 dB로 설정하였으며 모의실험 결과 Fig. 10과 같이 실제실험과 유사한 결과를 보임을 확인하였다. 이는 공분산 행렬의 고유값 분해 결과가 신호부분공간과 잡음부분공간을 분리하지 못하는 현상이 더욱 심하게 발생하기 때문이다.
또한, 일반 빔형성의 경우 표적신호의 도래각이 90°에 가까울수록 공간상에서 나타나는 위상차가 줄어들어 도래각이 0° 근처인 경우에 비해 빔폭이 증가하게 되는 한계점이 존재한다. 무격자 압축 빔형성의 경우 표적신호의 도래각이 90°에 가까울수록 조향벡터간의 상관값이 증가하여 해를 찾는 것이 어려워지는 한계점이 존재하나 해를 찾은 경우 빔폭이 증가하는 현상은 발생하지 않았으며 이는 마찬가지로 Figs. 7 ~ 9를 통해 확인 가능하였다.
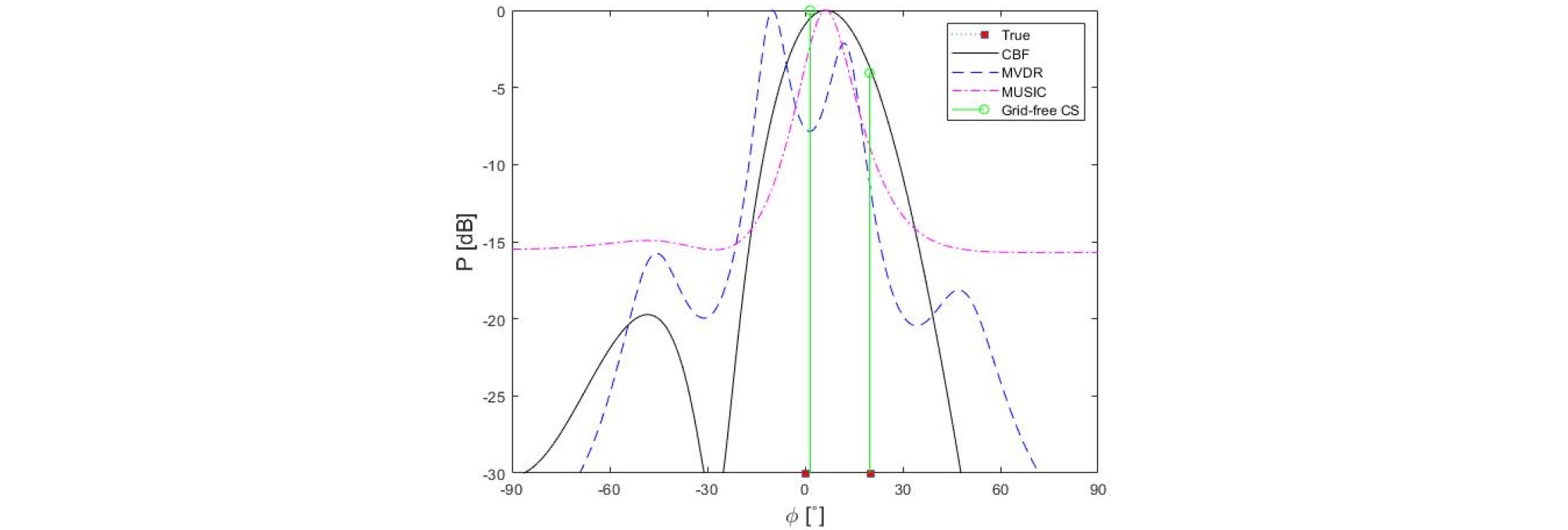
두 번째 실험은 20° 간격(0°, 20°) 그리고 15° 간격(0°, 15°)의 두 개의 상관 신호가 수신되는 환경에 대해서 수행하였다. 20° 간격의 두 상관 신호가 들어오는 경우 Fig. 11에서 확인할 수 있듯이 무격자 압축 빔형성만이 2개의 표적신호 도래각을 추정하였으며 이는 모의실험(Fig. 12)의 결과가 유사함을 할 수 있다. 15도 간격의 두 상관 신호가 들어오는 경우는 Fig. 12와 같이 무격자 압축 빔형성 또한 두 신호의 도래각을 구분하지 못하였는데 동일한 신호를 이용하여 무격자 압축 빔형성 Eq. (25)의 값에 변화를 주었을 때 Fig. 13과 같이 두 신호의 도래각을 구분할 수 있음을 확인할 수 있다. 이는 값이 고정된 값이 아닌 신호 대 잡음비에 따라 변화를 해주어야하는 값으로 무격자 압축 빔형성을 사용하기 위해서는 값을 적절히 설정해줘야 한다는 한계점을 확인하였다.
IV. 결 론
본 논문에서는 일반 빔형성, 적응 빔형성(MVDR, MUSIC) 그리고 무격자 압축 빔형성의 이론적 배경 및 한계점을 소개하였으며 모의실험 및 실제 실험을 통해 각 기법들의 성능을 확인하였다. 실제 실험을 통해 각 기법들의 성능이 모의실험과 유사한 결과를 보여줌을 확인하였으나 반사 신호가 존재하는 환경에서 적응 빔형성(MVDR, MUSIC)의 경우 그 성능이 크게 저하됨을 확인하였다. 무격자 압축 빔형성의 경우 모의실험과 동일하게 실제실험에서도 가장 우수한 성능을 보였으며 특히, 반사 신호와 상관신호가 존재하는 환경에서도 우수한 결과를 보임을 확인하였다. 그러나 설정된 정규화 변수(regularization parameter, )값에 따라 실제 신호의 도래각을 구분하지 못하는 한계점 또한 실제 실험을 통해 확인 할 수 있었다.