I. 서 론
II. 가중 해밍 거리 기반 이진 핑거프린트 정합
2.1 차분 기반 이진 핑거프린트와 파워 마스크기반 핑거프린트 정합
2.2 제안한 파워 웨이트 기반 핑거프린트 정합
2.3 코드북 기반 파워 웨이트 압축
III. 실험 결과
IV. 결 론
I. 서 론
핑거프린팅은 생체 식별에서 사람의 지문, 홍채 등을 이용하여 그 사람을 인식하는 것처럼 콘텐츠의 특징을 이용하여 해당 콘텐츠를 식별하는 기술을 말하며, 검색 서비스를 위한 핵심 기술이다.[1], [2], [3] 이 때 사용되는 특징을 핑거프린트 또는 해시라고 부른다. 핑거프린트의 형태는 이진수 또는 실수 형태를 가질 수 있으며, 본 논문에서는 이진수 형태의 핑거프린트를 다룬다. 콘텐츠 식별 시스템은 인식 대상 콘텐츠들의 핑거프린트를 추출하여 해당 콘텐츠의 정보인 메타데이터와 함께 미리 Date Base(DB)에 저장시켜두고, 식별이 필요한 입력 콘텐츠의 핑거프린트로 DB를 검색하여 입력 콘텐츠의 메타 정보를 찾는 것이다. 콘텐츠 식별에 사용되는 핑거프린트는 다음 4가지 조건들을 만족시켜야한다.[3]
∙ 차별성(pairwise independence):서로 다른 음악에 대해서 오인식이 일어나지 않도록 충분한 차별성을 가지고 있어야함
∙ 강인성(invariance to distortions):오디오 신호가 압축, EQ, 잡음첨가, sampling rate 변화 등 다양한 변환을 겪어 신호에 변화가 가해지더라도 그 값이 일정한 범위 내에서 유지되어야함
∙ 간결성(compactness):다수의 오디오에서 핑거프린트를 추출해서 저장하므로, 작은 크기의 표현이 필요함
∙ 계산용이성(computational efficiency):핑거프린트 추출에 있어서 계산량과 걸리는 시간이 작아야함
일반적으로 오디오 식별을 위해서는 차별화되고 강인성이 있는 특징을 추출한 후 이진화하여 간결한 형태로 만들어 핑거프린트를 만든다. 특징 추출 및 이진화 과정에서 정보의 손실이 발생하며, 따라서 이진수 형태의 핑거프린트만으로는 오디오 식별 성능을 개선하는 것이 어렵다. 오디오 식별 성능을 제고하기 위한 방법의 하나로 핑거프린트 추출 과정 중에 얻어지는 부가정보를 핑거프린트 정합의 가중치로 사용하는 파워 마스크 방법이 제안되었다.[4], [5] 파워 마스크는 핑거프린트 추출 과정에서 각 핑거프린트 비트의 예상 강인도를 추정한 것으로, 저장 공간을 줄이기 위해서 이진화를 통해서 강인한 비트와 연약한 비트로 나누어 저장한다. 본 논문은 파워 마스크를 개선한 파워 웨이트 방법을 제안한다. 기존 파워 마스크 방법은 예측 강인도를 이진화하는 과정에서 강인도 정보의 유실이 크지만 제안한 파워 웨이트는 강인도 정보를 그대로 사용할 수 있는 장점이 있다. 기존의 파워 마스크 방법은 이진화를 통해 파워 마스크를 저장하기 위해서 필요한 저장공간이 핑거프린트 저장공간의 크기와 같지만, 제안한 파워 웨이트는 파워 마스크와 비교하여 저장 공간이 많이 필요한 단점이 있다. 이를 개선하기 위해서 예측 강인도가 시간축 방향으로 상관도가 높으며, 음악의 경우 같은 노래 안에서 반복적으로 유사한 신호 패턴이 관찰되는 경우가 많다는 성질을 이용하여 파워 웨이트 압축 방법을 제안한다. 공개된 음악 데이터셋에서 실험을 수행하여, 파워 웨이트를 압축하기 전과 압축한 후의 성능을 기존 파워 마스크와 비교 분석하였다.
II. 가중 해밍 거리 기반 이진 핑거프린트 정합
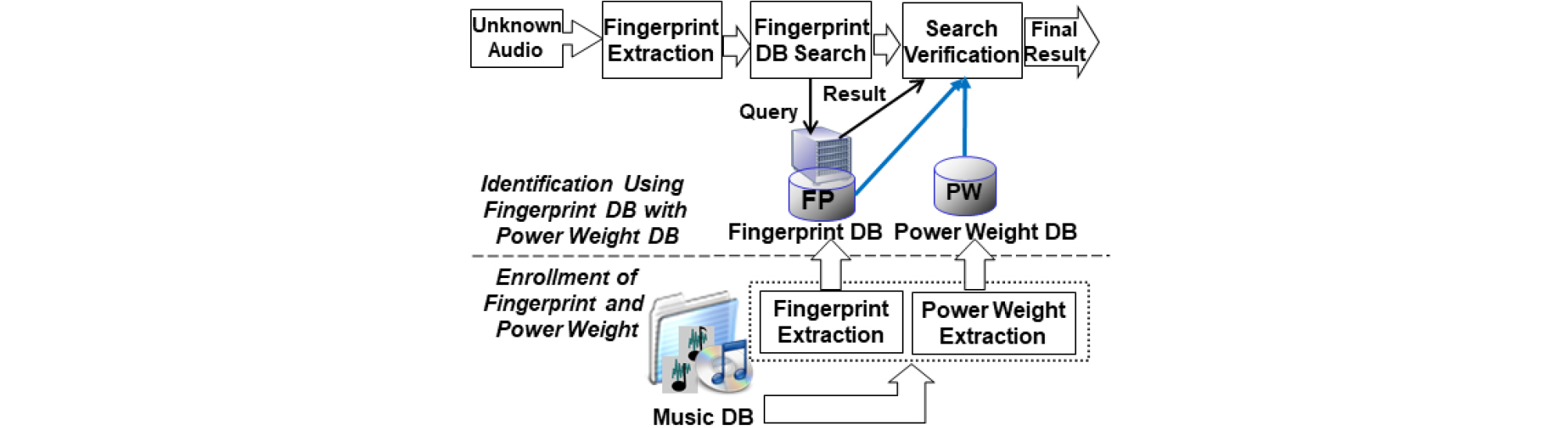
대표적인 핑거프린팅 방법인 차분 기반 이진 해시 Philips Robust Hash(PRH)[1]에 가중 해밍 거리를 적용하였다. Fig. 1에 주어진 바와 같이 검색 대상 오디오들로부터 핑거프린트 DB를 구축할 때 파워 웨이트도 같이 추출하여 DB를 구성하고, 미지의 오디오에 대해서 검색을 수행할 때 가중치로 활용하게 된다. 기존 파워 마스크 방법을 살펴보고, 파워 웨이트 방법을 제안한다.
2.1 차분 기반 이진 핑거프린트와 파워 마스크기반 핑거프린트 정합
본 논문은 이진 오디오 핑거프린팅 방법 중에서 대표적인 방법인 PRH에 가중치 기반 핑거프린트 정합을 적용한다. 먼저 PRH를 살펴보고, 기존 이진수 형태의 가중치 적용 방법인 파워 마스크 방법을 소개한다.
PRH 추출을 위해서 먼저 음악 신호의 n번째 프레임의 m번째 부밴드의 에너지를 En,m이라고 하자. 이 때 부밴드는 33개로 구성되며 오디오 스펙트럼의 300 Hz에서 2000 Hz 사이를 로그 스케일로 나누어서 만들어진다. 다음 Eq. (1)과 같이 부밴드 에너지 값을 시간과 주파수 축 방향으로 차분 필터링하여 F[n,m]을 구한다.
| $$F\lbrack n,m\rbrack=E_{n,m}-E_{n,m+1}-E_{n-1,m}+E_{n-1,m+1}.$$ | (1) |
다음과 같이 차분 필터된 에너지 값의 부호에 따라 핑거프린트 비트를 구한다.
| $$H\lbrack n,m\rbrack=\left\{\begin{array}{l}1\;\;\;if\;F\lbrack n,m\rbrack>0\\0\;\;\;if\;F\lbrack n,m\rbrack\leq0.\end{array}\right.$$ | (2) |
매 프레임마다 33개의 부밴드로부터 차분필터링 후 부호를 취하여 이진화를 수행하므로 32 비트가 얻어진다(M = 32). 한 프레임으로부터 얻은 32 비트 만으로는 음악을 인식할 수 없으므로 256개의 연속된 프레임을(N = 256) 사용하여, M행 N열 핑거프린트 블록(총 8192 비트)을 음악 인식을 위한 핑거프린트 정합에 사용한다.[1] 두 핑거프린트 블록 H1과 H2 사이의 해밍 거리 DH는 개별 비트간 거리인 d[n.m] = XOR (H1[n,m], H2[n.m])이라면 다음과 같이 주어진다.
| $$D_H(H_1,H_2)=\frac1{NM}\sum_{n=1}^N\sum_{m=1}^Md\lbrack n,m\rbrack.$$ | (3) |
비교 대상 두 핑거프린트 블락 간에 해밍 거리 기반 정합에서 8192 비트 중에서 65 % 이상 동일할 경우 두 핑거프린트 블락이 같은 음악 신호로부터 나왔다고 판정할 수 있음이 이론 및 실험적으로 검증되었다.[1]
해밍 거리 기반 핑거프린트 정합의 성능을 개선하기 위해서 핑거프린트 비트의 예측 강인도인 파워 마스크를 이용한 방법이 제안되었다.[4] 이진수 형태의 예측 강인도인 파워 마스크는 다음과 같이 구해진다. 먼저 각 프레임 별로 차분필터링을 수행한 후 차분의 크기인 |F[n,m]|의 값들을 크기순으로 정렬하고, 가장 큰 T 개의 값을 가지는 비트의 위치를 구한다. 그 T 개의 비트 위치의 값을 1로, 나머지 32-T개의 비트 위치의 값을 0으로 하면 32비트 파워 마스크 P[n,m]이 얻어진다. 기존 논문[4]에서 T = 24를 사용했으며, 이는 프레임 별로 24개 비트는 강인한 비트로 파워 마스크 값을 1로 설정하고, 8개 비트는 연약한 비트로 파워 마스크 값을 0으로 설정한 것이다. 이렇게 구한 파워 마스크 P[n,m]을 이용하면, 두 핑거프린트 블락 H1과 H2 사이의 가중치 기반 해밍거리 DM 을 강인한 비트와 연약한 비트에 대해서 서로 다른 가중치 α와 β를 사용하여 다음과 같이 구하게 된다(본 논문에서 α = 0.5, β = 1 사용함).[4]
2.2 제안한 파워 웨이트 기반 핑거프린트 정합
기존 파워 마스크 방법은 예측 강인도 정보를 그대로 가중치로 사용하지 않고, DB 저장공간을 줄이기 위해서 이진화하였다. 본 논문에서는 예측 강인도를 이진수가 아닌 실수 형태의 가중치로 사용하는 파워 웨이트 방법을 제안한다. 오디오 잡음의 종류 및 소리의 크기가 다양하므로, 핑거프린트 DB를 구축할 때 예측 강인도를 정밀하게 계산하는 것은 불가능하다. 따라서 기존 파워 마스크 방법은 Eq. (1)의 에너지 차분의 크기인 |F[n,m]|의 값이 클수록 예측 강인도가 클 것으로 가정하고 파워 마스크를 유도하였다. 제안한 파워 웨이트 방법에서도 마찬가지로 |F[n,m]|의 값이 클수록 예측 강인도가 클 것으로 가정한다. 먼저 n번째 프레임의 |F[n,m]|의 값을 크기순으로 오름차순으로 정렬할 때 |F[n,m]|의 순위를 Rn[m]이라 하자. 순위 벡터 Rn[m]은 n번째 프레임에서 m번째 에너지 차분값인 |F[n,m]|의 크기 순위로써 크기 순서에 따라 순위 값인 1부터 32까지의 값을 가지게 된다. 즉 |F[n,m]|의 값이 가장 큰 부밴드에서는 32의 값을 가지고, 가장 작은 부밴드에서는 1의 값을 가진다. 순위 Rn[m]이 클수록 파워 웨이트 W[n,m]도 커져야한다. 본 논문에서는 파워 웨이트 W[n,m]이 0.5에서 0.9 사이의 값을 가진다고 가정하였다. 즉 확률적으로 가장 크기 값이 작은 핑거프린트 비트의 예측 강인도는 0.5(즉, 50 % 정합 성공 확률) 이고, 가장 크기 값이 큰 핑거프린트 비트의 예측 강인도는 0.9(즉, 90 % 정합 성공 확률)로 가정하였다. 어떠한 변형이나 잡음이 가해질지 예상하기 어려우므로, 파워 웨이트의 형태를 정밀하게 정하는 것은 불가능하다. 따라서 본 논문에서는 Rn[m]에 대해서 증가하면서 각각 볼록, 선형, 오목 함수인 다음 3가지 형태의 파워 웨이트 W[n,m]을 고려하였다.
| $$W\lbrack n,m\rbrack=0.5+0.4(\frac{R_n\lbrack m\rbrack-1}{M-1})^2.$$ | (5) |
| $$W\lbrack n,m\rbrack=0.5+0.4(\frac{R_n\lbrack m\rbrack-1}{M-1}).$$ | (6) |
| $$W\lbrack n,m\rbrack=0.9-0.4(\frac{R_n\lbrack m\rbrack-1}{M-1}-1)^2.$$ | (7) |
파워 웨이트 W[n,m]을 이용한 두 핑거프린트 블록 H1과 H2 간의 정합 DW는 다음과 같이 주어진다.
| $$D_W(H_1,H_2)=\frac{\sum_{n=1}^N\sum_{m=1}^MW\lbrack n,m\rbrack d\lbrack n,m\rbrack}{N\sum_{m=1}^MW\lbrack n,m\rbrack}.$$ | (8) |
제안한 DW와 기존 DM 모두 가중 해밍 거리로써 d[n,m] 이 1 또는 0의 값을 가지므로, 기존 해밍 거리 DH와 비교하여 곱하기 횟수의 증가 없이 가산으로 구현할 수 있으므로 실제 구현에서 계산량 증가는 크지 않다.
2.3 코드북 기반 파워 웨이트 압축
기존 이진수 파워 마스크와 비교하여, 제안한 파워 웨이트는 실수값 형태로 예측 강인도를 그대로 핑거프린트 정합에 반영할 수 있는 장점이 있지만 저장 공간이 많이 소요되는 단점이 있다. 저장 공간이 늘어나는 단점을 보완하기 위해서 파워 웨이트 코드북을 만들어 파워 웨이트 수열을 코드 수열로 변환하는 압축 방법을 제안한다. 일반적으로 음악 신호는 장르, 사용된 악기 등의 특성에 따라 특정 대역 스펙트럼 성분이 상대적으로 크거나 작은 경우가 많으며, PRH는 각 대역의 에너지 차이를 이용하므로 특정 대역의 파워 웨이트 값이 크거나 작을 확률에 차이가 존재한다. 또한 음악 신호는 시간적으로 상관관계가 크므로, 인접 프레임들의 파워 웨이트는 비슷한 형태를 가지게 된다. 이러한 음악 신호의 성질을 이용하여 각 음악 파일 별로 자주 사용되는 파워 웨이트들로 코드북을 만들고 각 프레임의 파워 웨이트를 코드북에서 가장 가까운 코드에 할당하여 압축할 수 있다. 본 논문에서는 효율성이 높은 파워 웨이트 코드북을 학습하기 위해서 음악 파일 별로 코드북을 따로 구성한다. 음악 파일의 파워 웨이트 코드북은 K개의 M차원 벡터로 이루어지며, k번째 M차원 코드를 Ck 라고 하면 다음과 같이 n번째 프레임에서 순위 벡터 Rn과 내적이 가장 큰 코드를 파워 웨이트로 정하게 된다.
| $$\gamma_n=\begin{array}{c}\mathrm{argmax}\\1\leq k\leq K\end{array}\sum_{m=1}^M\left\langle R_n\lbrack m\rbrack,\;C_k\lbrack m\rbrack\right\rangle.$$ | (9) |
음악 파일의 전체 프레임 개수가 L이라면 코드북 Ck 학습을 위해서 다음 목적함수 OC를 최대화한다.
| $$O_C=\sum_{n=1}^L\sum_{m=1}^MR_n\lbrack m\rbrack C_{\gamma_n}\lbrack m\rbrack.$$ | (10) |
Eq. (10)의 목적함수를 최대화시키는 코드북을 찾기 위해서 k-means 방법처럼 반복적으로 코드북을 업데이트 하였다. 먼저 해당 음악의 파워 웨이트들 중에서 임의로 K개의 파워 웨이트를 선택하고, 음악 파일 내의 L개의 프레임을 선택된 K개의 파워 웨이트들 중 하나로 Eq. (9)와 같이 정합이 가장 큰 것으로 배정한다. 즉 L개의 프레임을 K개의 파워 웨이트들 중 하나로 할당하고, 각 코드에 할당된 프레임들의 순위 벡터를 더하고, 순위 벡터를 더한 값을 오름차순으로 정렬하여 새로운 순위 벡터를 만든 후에 그 순위벡터에 해당하는 파워 웨이트를 코드북으로 업데이트 한다. 더 이상 코드북 업데이트가 일어나지 않을 때까지 이 과정을 반복하여 코드북을 만들게 된다. 최종적으로 만들어진 코드북을 이용하여 해당 음악 신호의 각 프레임의 파워 웨이트를 부호화하게 된다. 코드북이 K개의 파워 웨이트를 코드로 하고 있다면 log2(K) 비트로 각 프레임의 파워 웨이트를 부호화할 수 있으므로 저장 공간을 줄일 수 있다. 물론 각 음악 파일별로 코드북을 만들어서 저장해야하므로 코드북 크기만큼의 추가적인 저장 공간은 필요하다.
III. 실험 결과
본 장에서는 기존의 파워 마스크 기반 핑거프린트 정합과 제안한 파워 웨이트를 이용한 핑거프린트 정합의 성능을 비교한다. 성능 비교를 위해서 음원이 공개되어 있는 GTZAN 음악 장르 데이터셋과 음악/음성 분류 데이터셋을 사용하였다.[6] 장르 데이터셋은 블르스, 클래식, 컨츄리, 디스코, 힙합, 재즈, 메탈, 팝, 레게, 락의 10개의 장르에 각각 100곡씩 30 s 길이의 1000개의 음악파일로 이루어져있다. 분류 데이터셋은 30 s 길이의 음악과 음성 파일 각 64개씩으로 총 128개 파일로 이루어져 있다. 각 음악 파일에 음성 파일 64개를 음악 λ와 음성 (1-λ) 비율로 합성하여 합성 파일 4096개로 이루어진 음악음성 합성 데이터셋을 만들었다. 실험에서는 λ값을 0.2와 0.5의 값을 사용하였다. 각 실험데이터셋에 PRH 방법으로 핑거프린트와 제안한 파워 웨이트를 추출하여 핑거프린트 DB를 만들어서 핑거프린트 정합 실험을 수행하였다.
일반적으로 콘텐츠 식별 시스템의 성능 비교에는 Receiver Operating Characteristic(ROC) 곡선이 이용된다. ROC 곡선은 인식 시스템에 존재하는 두 가지 형태의 오인식율인 False Alarm Rate(FAR)과 False Rejection Rate(FRR)을 가로와 세로축으로 하여 그래프를 그린 것이다. 오디오 핑거프린팅 시스템에서 FAR은 서로 다른 오디오를 같다고 판정할 확률이며, FRR은 같은 오디오를 다르다고 판정할 확률이다. 기존 해밍 거리 DH, 파워 마스크 기반 거리 DM, 파워 웨이트 기반 거리 DW를 공정하게 비교하기 위해서 ROC 곡선을 구하였다. 기존 논문[1]에서처럼 매 3 s 구간의 오디오 신호의 핑거프린트(즉, N = 256, M = 32이므로 총 8192 비트)를 이용하여 핑거프린트 정합을 수행하여 ROC 곡선을 얻었다. FAR을 구하기 위해서는 구축된 1000곡으로 이루어진 장르 데이터셋 핑거프린트 DB에서 임의로 선택된 핑거프린트 쌍들 간의 해밍 거리를 구하고, 오디오 식별기의 문턱값을 변화시켜가면서 문턱값 보다 작은 거리를 가지는 핑거프린트 쌍의 비율을 구하였다.
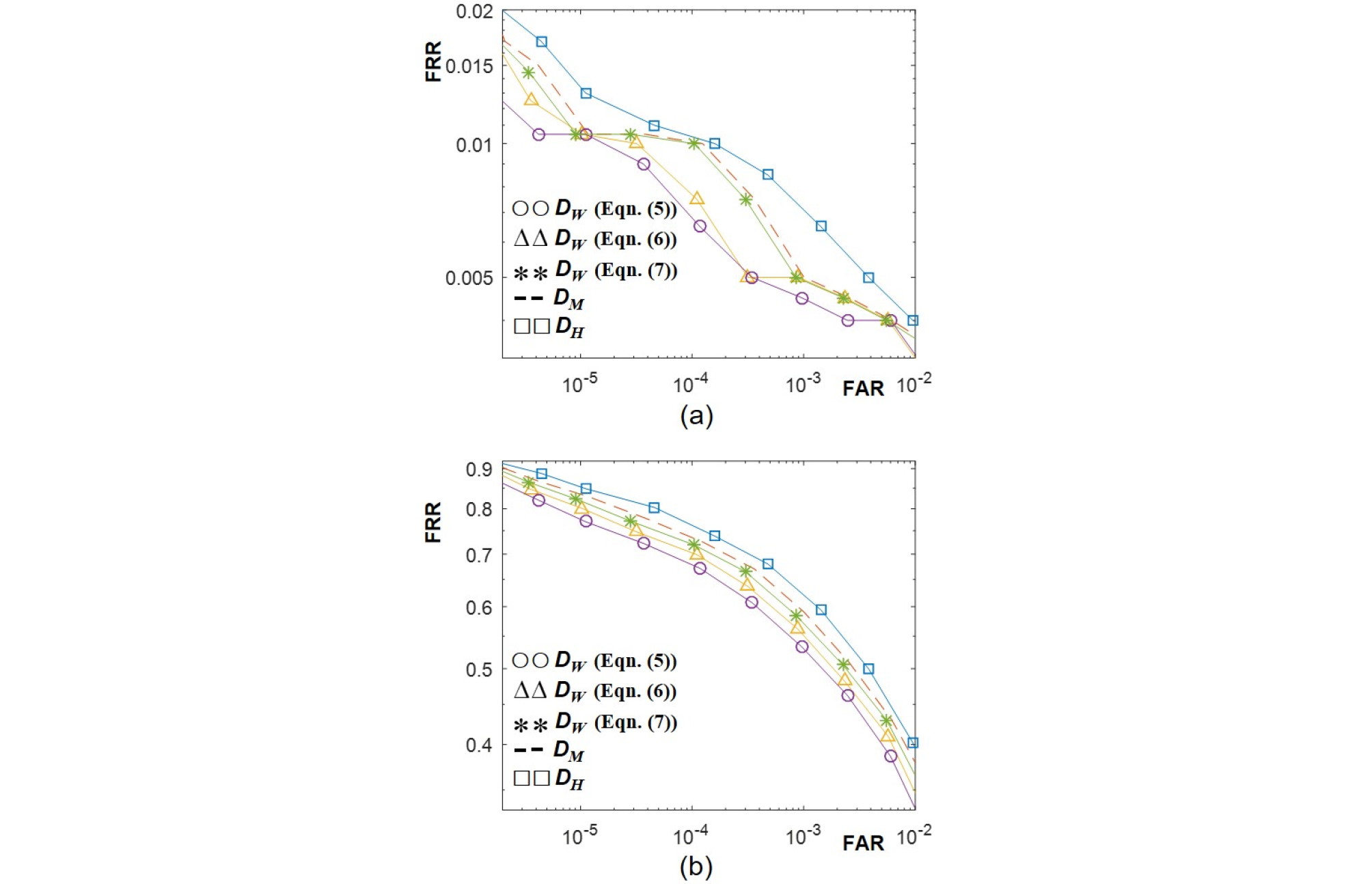
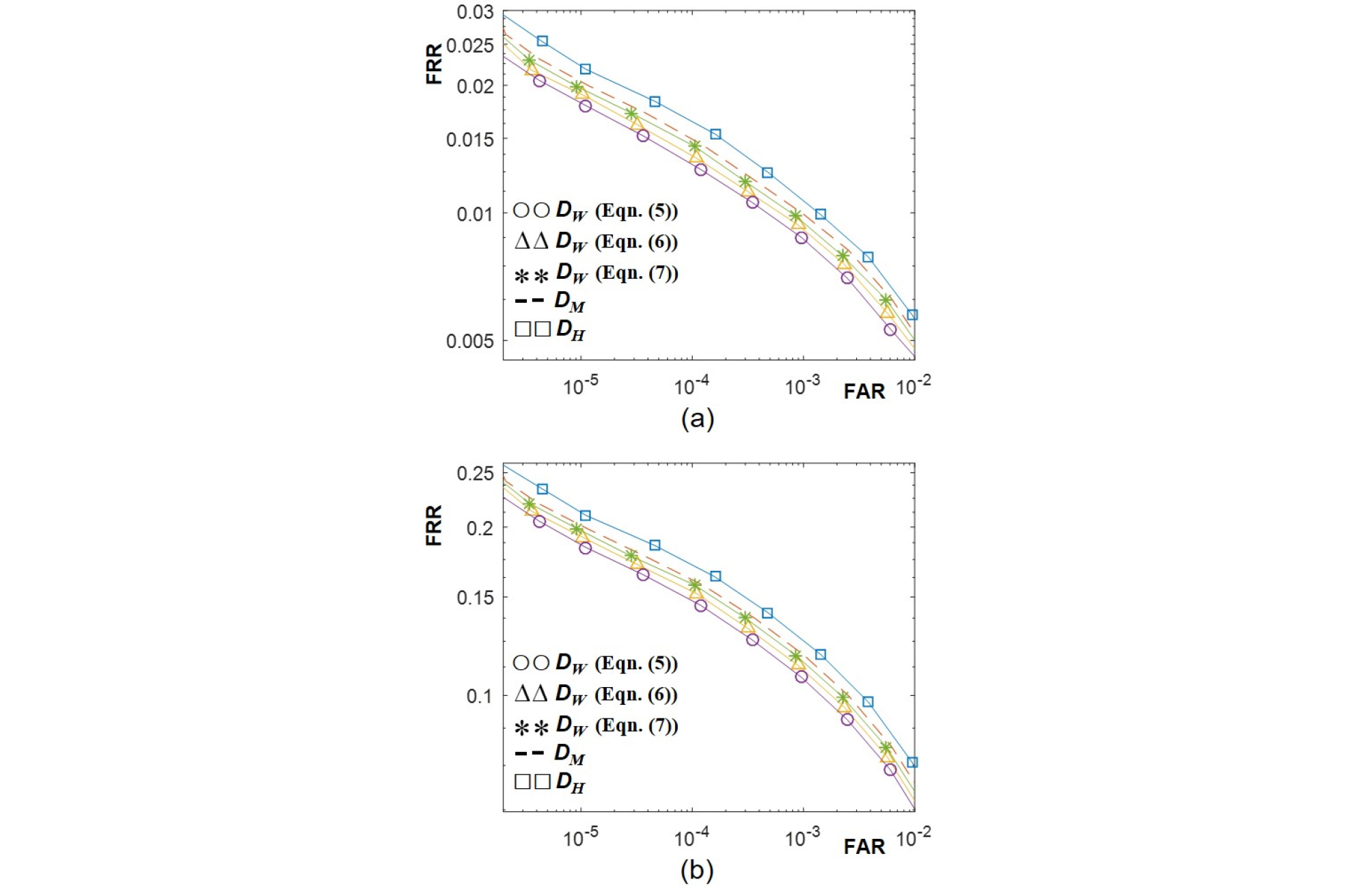
첫 번째 실험으로 백색 잡음에 대한 강인성을 실험하기 위해서 장르 데이터셋의 1000개의 음악 파일에 Signal-to-Noise Ratio(SNR)을 바꿔가면서 백색 잡음을 가산하였다. 본 논문에서는 SNR을 5 dB와 –10 dB를 사용하였다. 원본 음악의 핑거프린트와 백색 잡음이 가산된 음악에서 얻은 핑거프린트 간의 거리를 문턱값을 변화시켜가면서 문턱값보다 작은 거리를 가지는 핑거프린트 쌍의 비율을 구하여 FRR을 계산하였다. 구한 FAR과 FRR을 이용하여 얻은 ROC 곡선을 Fig. 2에 도시하였다. SNR값에 상관없이 기존 해밍 거리인 DH에 비해서 핑거프리트 추출 과정의 크기 순서를 활용한 DM과 DW를 이용한 방법들의 성능이 더 좋았다. 예측 강인도 함수의 형태와 상관없이 제안한 DW의 성능이 DM의 성능보다 좋았다. 파워 웨이트 기반 거리 중에서는 Eq. (5)의 볼록 함수를 예측 강인도로 사용한 것이 가장 좋은 성능을 보였고, Eq. (7)의 오목 함수 형태의 예측 강인도 성능이 가장 좋지 않았다. 즉, Eq. (1)의 |F[n,m]|의 값이 큰 위치의 핑거프린트 비트에 가중치를 상대적으로 더 크게 하여 차별성을 크게 하는 것이 정합 성능 향상에 도움이 됨을 알 수 있다. 두 번째 실험으로 음악과 음성 합성에 대한 강인성 실험을 수행하였다. GTZAN 음악/음성 분류 데이터셋에서 얻은 음악음성 합성 데이터셋의 4096개의 파일에서 핑거프린트를 추출하고 원본 음악의 핑거프린트와 비교하여 FRR을 구하였다. Fig. 3은 음악음성 합성 데이터셋의 FRR을 GTZAN 장르 데이터셋에서 구한 FAR과 함께 도시하여 ROC 곡선을 구한 결과이다. 음악에 음성을 합성한 경우에도 Fig. 2의 백색 잡음 실험과 비슷한 경향성을 보였다. 이를 통해서 다양한 형태의 잡음에 대해서 제안한 파워 웨이트 방법이 정합 성능을 개선함을 확인하였고, 예측 강인도 함수는 볼록 함수를 사용하는 것이 성능 제고에 도움이 됨을 보였다.
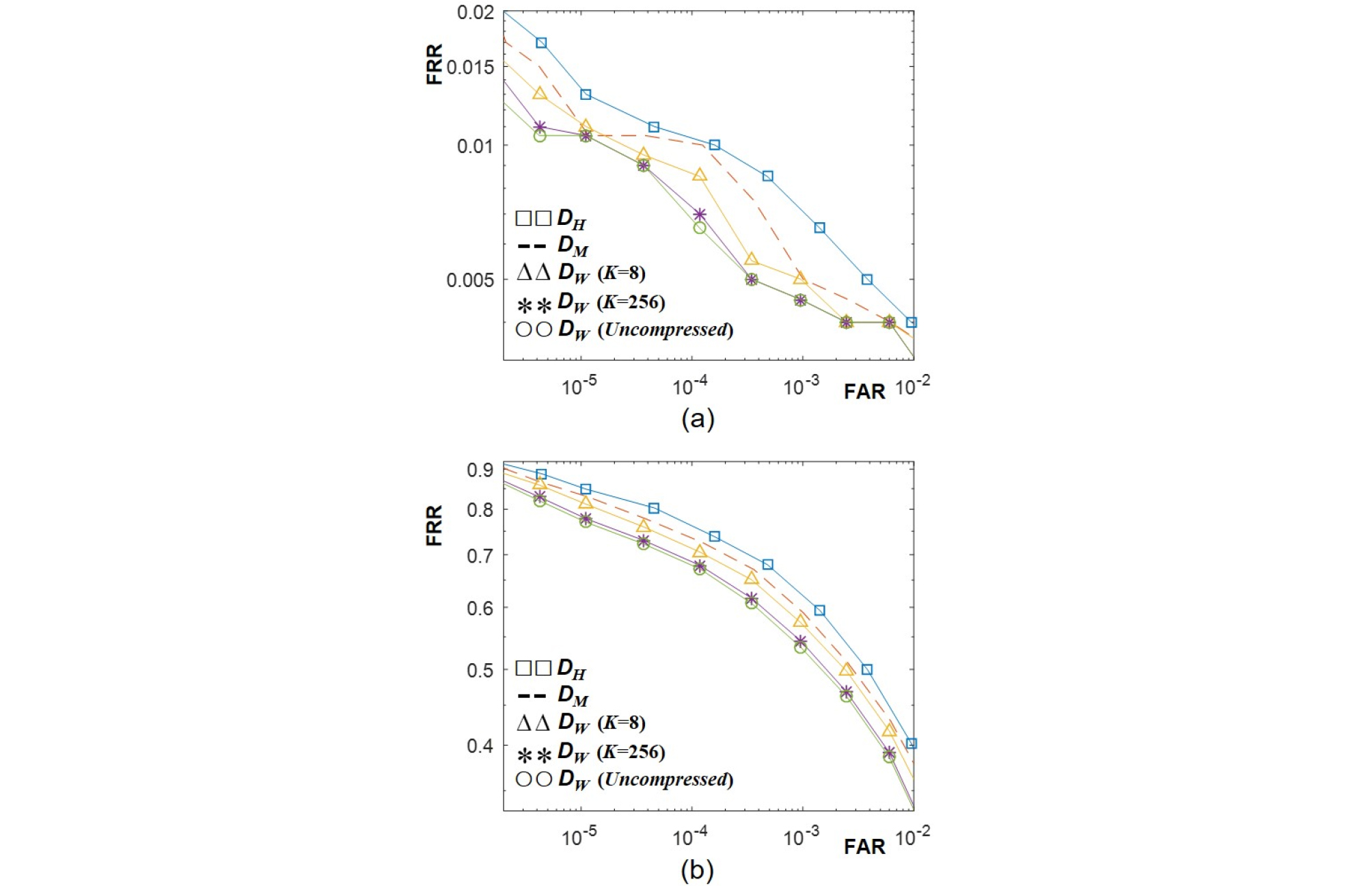
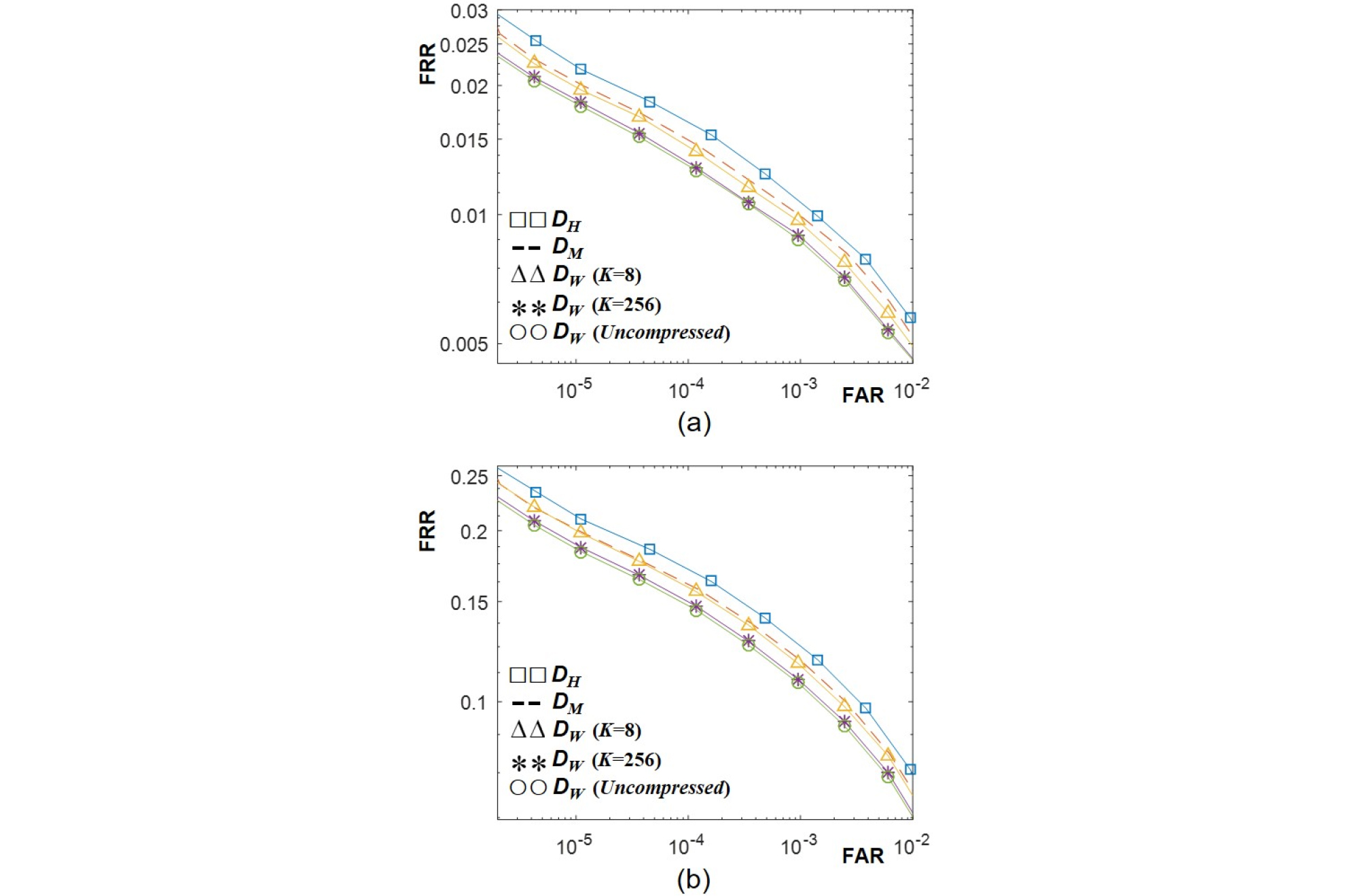
파워 웨이트를 코드북 기반으로 압축한 경우의 성능을 압축하지 않은 파워 웨이트의 성능과 비교하여 백색잡음과 음악음성 합성 데이터셋에 대해서 실험을 수행하여 각각 Figs. 4와 5에 도시하였다. 예측 강인도 함수는 Eq. (5)의 볼록 함수를 사용하였다. 원본 음악으로부터 핑거프린트와 파워 웨이트를 추출하고, 파워 웨이트를 압축하였다. 각 음악 파일 별로 파워 웨이트 코드북을 학습하였으며, 코드북의 크기인 K는 8과 256을 사용하였다. 백색 잡음과 음성 합성 모두에서 코드북 크기인 K값을 작게 하면 DW의 성능이 열화됨을 알 수 있다. 코드북 크기가 줄어들면, 압축 전의 파워 웨이트와의 차이가 커지게 되는데 이로 인해 파워 웨이트 효과가 감소하게 된다. 하지만 코드북 크기인 K값을 8까지 줄이더라도(즉, 파워 웨이트 저장에 프레임당 3 비트 소요) 기존 파워 마스크 기반 거리인 DM 보다 성능이 우수함을 확인하였다. Figs. 4와 5 모두에서 K = 256을 사용하면(즉, 파워 웨이트 저장에 프레임당 8 비트 소요), 압축하지 않은 파워 웨이트 기반 거리의 정합 성능에 근접하였다. 실험 결과 대략적으로 음악 신호 길이의 1/10 정도만 코드북으로 사용하면 압축 하지 않은 파워 웨이트와 거의 유사한 수준의 성능을 얻을 수 있음을 알 수 있었다.
IV. 결 론
오디오 핑거프린트 정합 성능을 제고하기 위하여 파워 웨이트 방법을 제안하였다. 예측 강인도 함수를 직접 가중치로 핑거프린트 정합을 수행함으로써 가중치를 이진화 하는 기존 파워 마스크 방법에 대비하여 성능을 개선하였다. 또한 파워 웨이트의 코드북을 학습하여 코드 비트로 변환함으로써 예측 강인도를 저장하는데 소요되는 저장 공간을 줄였다. 공개된 음악 데이터셋에서 실험을 수행하여, 제안된 파워 웨이트가 오디오 핑거프린트 정합 성능을 제고하고, 코드북 학습을 통해서 정합 성능의 큰 열화 없이 파워 웨이트를 압축할 수 있음을 보였다.