Earthquake events classification using convolutional recurrent neural network

Bonhwa Ku; Gwantae Kim; Su Jang; Hanseok Ko

doi:10.7776/ASK.2020.39.6.592

Preview

Research Article

The Journal of the Acoustical Society of Korea. 30 November 2020. 592-599
https://doi.org/10.7776/ASK.2020.39.6.592

Earthquake events classification using convolutional recurrent neural network

합성곱 순환 신경망 구조를 이용한 지진 이벤트 분류 기법

Bonhwa Ku¹

Gwantae Kim¹

Su Jang¹

Hanseok Ko¹^*

구 본화¹

김 관태¹

장 수¹

고 한석¹^*

¹고려대학교 전기전자전파 공학부

^{*Corresponding Author}

ABSTRACT

This paper proposes a Convolutional Recurrent Neural Net (CRNN) structure that can simultaneously reflect both static and dynamic characteristics of seismic waveforms for various earthquake events classification. Addressing various earthquake events, including not only micro-earthquakes and artificial-earthquakes but also macro-earthquakes, requires both effective feature extraction and a classifier that can discriminate seismic waveform under noisy environment. First, we extract the static characteristics of seismic waveform through an attention-based convolution layer. Then, the extracted feature-map is sequentially injected as input to a multi- input single-output Long Short-Term Memory (LSTM) network structure to extract the dynamic characteristic for various seismic event classifications. Subsequently, we perform earthquake events classification through two fully connected layers and softmax function. Representative experimental results using domestic and foreign earthquake database show that the proposed model provides an effective structure for various earthquake events classification.

Keywords

Earthquake events classification

Convolutional Neural Network (CNN)

Recurrent Neural Network (RNN)

Convolutional Recurrent Neural Network (CRNN)

본 논문은 다양한 지진 이벤트 분류를 위해 지진 데이터의 정적인 특성과 동적인 특성을 동시에 반영할 수 있는 합성곱 순환 신경망(Convolutional Recurrent Neural Net, CRNN) 구조를 제안한다. 중규모 지진뿐만 아니라 미소 지진, 인공 지진을 포함한 지진 이벤트 분류 문제를 해결하려면 효과적인 특징 추출 및 분류 방법이 필요하다. 본 논문에서는 먼저 주의 기반 합성곱 레이어를 통해 지진 데이터의 정적 특성을 추출 하게 된다. 추출된 특징은 다중 입력 단일 출력 장단기메모리(Long Short-Term Memory, LSTM) 네트워크 구조에 순차적으로 입력되어 다양한 지진 이벤트 분류를 위한 동적 특성을 추출하게 되며 완전 연결 레이어와 소프트맥스 함수를 통해 지진 이벤트 분류를 수행한다. 국내외 지진을 이용한 모의 실험 결과 제안된 모델은 다양한 지진 이벤트 분류에 효과적인 모습을 보여 주었다.

키워드

지진 이벤트 분류

합성곱 신경망

순환 신경망

합성 순환 신경망

MAIN

I. 서 론
II. 지진 이벤트 분류를 위한 CRNN 구조
2.1 Preprocessing
2.2 주의 기반 Convolutional Neural Network
2.3 Long Short-Term Memory Networks
2.4 Classifier
III. 데이터셋
IV. 모의 실험
4.1 실험 환경
4.2 모델에 따른 분류 성능 분석
4.3 전처리에 따른 분류 결과 분석
4.4 LSTM time step에 따른 분류 결과 분석
V. 결 론

I. 서 론

시계열 데이터 분류는 음성 인식, 금융학, 지진학 등 다양한 분야에서 발생한다. 전통적인 특징 기반 시계열 분류에서는 특징 추출과 학습기의 파라메터들을 전문가의 경험적/실험적 요소에 따라 설정하게 된다. 최근에 영상 분류에서 합성곱신경망(Convolutional Neural Network, CNN)과 같은 딥러닝의 성공으로 인해 다양한 분야에서 딥러닝과 접목된 기술들이 활발히 연구되고 있다.^[1,2,3,4] 시계열 분류 문제에서도 기존의 방식과 딥러닝이 접목되어 분류 문제에 적합한 특징 추출 및 분류기를 학습하는 방식들이 연구되고 있다.^[5,6]

STA/LTA 방식은 단기 평균(Short Time Average, STA)과 장기 평균(Long Time Average, LTA)의 비율 문턱치를 통해 지진을 탐지하는 대표적인 방식으로 낮은 Signal to Noise Ratio (SNR) 환경에서는 적절하지 못하다.^[7] 자기상관(autocorrelation) 기반 방식은 동일 지역에서 반복되는 지진 파형들간의 상관을 기반으로 지진을 탐지하는 방식으로 성능은 우수하지만 연산량 과부하 및 입력 신호가 길 경우 활용성에 한계를 지니고 있다.^[8] 템플릿 매칭(template matching) 방식은 자기상관 방법의 연산량 과부하 문제를 개선하기 위해 제안된 방법으로 지진 템플릿을 설정 후 템플릿형과의 상관관계를 통해 지진을 탐지하게 된다.^[9] 주성분 분석(principle component analysis) 혹은 부공간 학습(subspace learning)을 통해 템플릿의 숫자를 줄이는 템플릿매칭 방식들과 Fingerprint And Similarity Thresholding(FAST)^[10]와 같이 템플릿 매칭의 연산량을 개선하기 위한 방식들이 제안되고 있다.

딥러닝을 적용한 지진 이벤트 분류/탐지 기법도 다양하게 보고 되고 있다.^[11,12,13] ConvQuakeNet^[11]에서는 10 s의 3채널 미가공 지진파 데이터를 사용하여 지진 이벤트 분류를 위한 합성곱신경망 모델을 제안하였다. 제안된 방식의 구조는 1-D 합성곱과 비선형 변환 Rectified Linear Unit(ReLU)을 가진 8개의 합성곱 레이어로 구성되어 있다. 합성곱 레이어를 통해 128차원의 특징을 추출하며 완전 연결 레이어를(fully-connected layer) 통해 지진/소음 분류 및 위치 추정이 수행된다. CRED^[12]는 지진 분류/탐지 문제를 3채널 지진의 스펙트로그램에서 시퀀스-시퀀스 학습으로 공식화했다. 이 모델은 2-D CNN을 사용한 특징 추출, 순환신경망(Recurrent Neural Net, RNN)을 통한 데이터 시퀀스 학습 및 완전 연결 레이어를 사용한 분류로 구성되었다. ConvQuakeNet 방법과는 달리 100 Hz로 기록 된 30 s의 원시 지진 데이터를 스펙트로그램으로 변환하고 2-D CNN을 사용하여 특징을 추출하였다.

본 논문에서는 다양한 지진 이벤트를 분류할 수 있는 합성곱 순환신경망(Convolutional Recurrent Neural Net, CRNN) 구조를 제안한다. 지진 데이터의 정적인 특성과 동적인 특성을 모두 반영한 모델을 통해 지진 여부 및 지진의 종류를 분류할 수 있는 모델을 제안한다. 먼저 합성곱 레이어서는 3 채널 미가공 지진파 데이터를 입력값으로 다양한 지진 이벤트 분류에 적합한 정적 특징들을 추출한다. 정교한 특징맵을 추출하기 위해 본 논문에서는 주의(attention) 기반 합성곱 레이어를 적용하였다. 주의 기법은 학습 모델이 중요한 특징에 더 초점을 맞출 수 있도록 특징맵을 구분성 있게 만들어 준다. 본 논문에서는 Squeeze Excitation(SE)^[14] 주의 모듈을 개선한 형태의 주의 기반 모듈이 적용된 합성곱 과정을 거치게 된다. 추출된 특징맵은 분리되어 순차적으로 장단기메모리(Long Short-Term Memory, LSTM)^[15] 셀에 입력되어 지진 데이터의 동적인 특성을 추출하며 완전 연결 레이어와 소프트맥스(Softmax) 함수를 통해서 지진 이벤트를 분류하게 된다. LSTM 네트워크에서 셀의 개수는 합성곱 레이어의 개수에 따라서 변동되며 본 논문에서는 지진 이벤트 분류에 적합한 셀의 개수를 제시하였다. 본 논문에서는 2016년부터 2019년도에 발생한 한반도 지진을 대상으로 제안한 알고리즘의 학습 및 테스트를 진행하였으며 다양한 실험을 통해 제안한 방법의 우수성을 입증하였다.

본 논문의 구성은 다음과 같다. 2장에서는 제안된 CRNN을 이용한 지진 이벤트 분류 기법을 제시하였으며 3장에서는 학습 및 테스트에 이용하는 지진 데이터의 수집에 관해 설명하였다. 4장에서는 제안된 알고리즘의 성능 평가를 다루며, 5장에서 결론을 맺는다.

II. 지진 이벤트 분류를 위한 CRNN 구조

본 논문에서 제안하는 CRNN 모델은 Fig. 1과 같이 3채널(HHE, HHN, HHZ) 지진 원시 데이터를 입력으로 전처리, 합성곱 블럭, LSTM 블럭, 분류기 블럭으로 구성된다.

https://static.apub.kr/journalsite/sites/ask/2020-039-06/N0660390611/images/ASK_39_06_11_F1.jpg

Fig. 1

(Color available online) Proposed CRNN structure.

2.1 Preprocessing

관측된 지진 데이터는 개별 관측소별 상이한 바이어스가 존재할 수 있다. 이러한 경우 Eq. (1)과 같이 중심화 과정을 거치게 되면 바이어스가 존재하는 데이터들을 원점으로 이동시키는 효과를 얻을 수 있다.

(1)

y_{m} = x_{m} - \frac{1}{M} \sum_{m}^{M} x_{m},

여기서 M은 데이터에서 총 샘플수를 나타낸다. 또한 수집된 학습 데이터의 경우 실제 관측한 지진 데이터를 이용하게 된다. 이러한 관측 데이터에는 순수한 지진 이벤트 데이터 이외에 저주파 잡음 성분도 포함되어 있다. 잡음 성분을 포함한 지진 이벤트를 효과적으로 분류하기 위해서는 지진 데이터에 공통적으로 포함되어 있는 저주파 잡음을 필터링을 통해 제거할 필요가 있다. 본 논문에서는 차단 주파수 2 Hz, 5차 Finite Impulse Response(FIR) 형태의 고역 통과 필터를 적용하였다.

2.2 주의 기반 Convolutional Neural Network

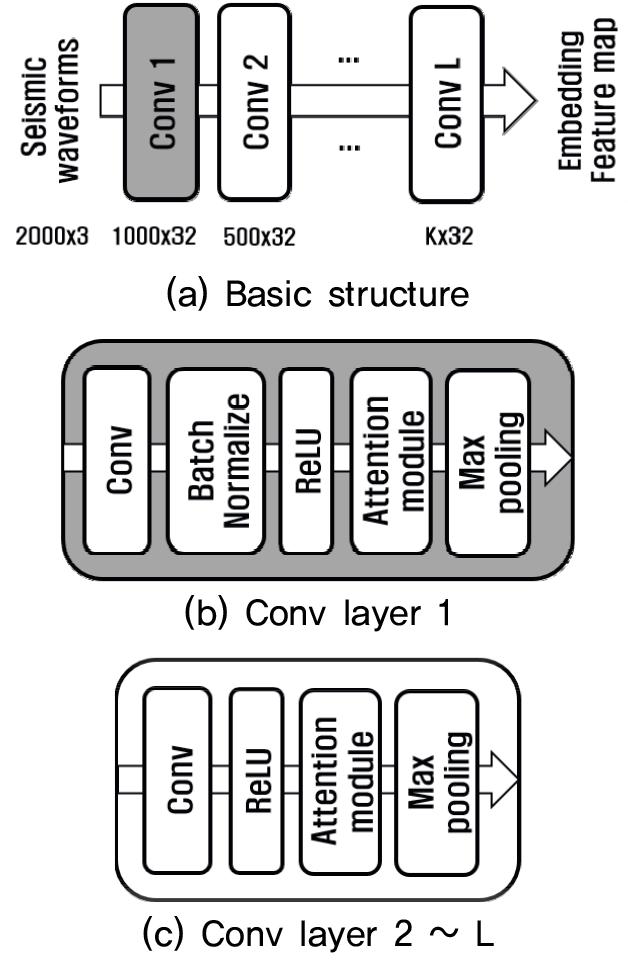
전처리 과정을 거친 지진 데이터는 주의 기반 CNN을 통해 지진 데이터의 정적인 특징을 추출한다. 본 논문에서 제안하는 주의 기반 CNN 구조는 Fig. 2와 같다. 제안된 구조에서 L개의 Conv 레이어로 구성하였으며 각 Conv 레이어는 공통적으로 합성곱, 비선형 변환 ReLU, 주의 모듈, max pooling의 과정을 수행한다. 합성곱 레이어는 Eq. (2)와 같이 1-D 합성곱을 수행하며 합성곱 결과는 Eq. (3)과 같은 ReLU 함수를 통해 비선형 변환을 거친다. 1-D convolution의 필터 크기는 3 × 1 형태를 사용하며 채널 C의 크기는 각 레이어마다 32개를 적용한다.

(2)

y_{c, t}^{l} = R (\sum_{c'}^{C} \sum_{t'}^{3} x_{c', t + t' - 1}^{l - 1} \cdot W_{c, c', t'}^{l}) for l = 1, . ., L,

여기서 c와 c'는 출력 채널 인덱스, 입력 채널 인덱스를 나타내며 t는 시간축 상의 인덱스를 나타낸다.

(3)

R (z) = \max (0, z) .

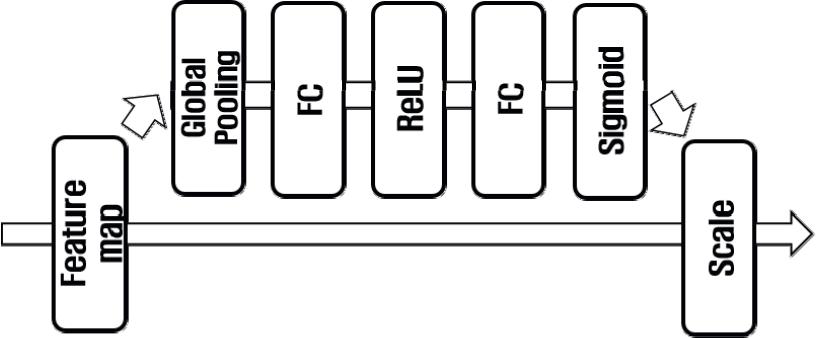
Conv 레이어 1에서는 일괄 정규화(batch normali- zation)^[16] 을 적용하여 각 관측소마다 다르게 관측될 수 있는 지진파의 크기를 정규화하는 효과를 얻을 수 있다. 그러나 모든 레이어에서 일괄 정규화를 적용할 경우 vanishing gradient 문제가 발생하여 첫번째 Conv 레이어에서만 사용하는 것으로 제한을 두었다. 각 Conv 레이어는 2 × 1 크기의 간격 2 인 최대 풀링을 사용하므로 Conv 레이어를 통과할 수록 특징의 크기는 이전 레이어의 출력 특징보다 1/2 크기로 줄어들게 된다. Conv L을 거친 지진파 데이터는 K 크기의 32채널 특징맵을 추출한다. 주의 모듈은 Fig. 2와 같이 ReLU와 최대 풀링 사이에 배치한다. 주의 모듈은 특징맵 중에서 주요한 구성 요소를 파악하여 특징맵을 향상시키는 기법이다. 본 논문에서는 Fig. 3과 같이 Squeeze Excitation Networks(SENET)에 기반하여 개선된 주의 모듈을 적용한다. SENET은 특징맵의 채널간 상호 종속성을 모델링하여 네트워크의 표현 능력을 향상시킨다. SENET은 압축(squeeze) 연산과 자극 조정(excitation) 연산으로 구성된다. 압축 연산은 특징맵의 핵심 정보를 유지하면서 특징맵을 공간적으로 축소한다. 압축 연산은 공간상에서 평균을 취하는 Global Average Pooling(GAP)을 주로 사용한다. 자극 조정 연산은 2개의 완전 연결된 레이어와 sigmoid 활성화 함수의 학습을 통해 추출된 특징맵 채널의 중요성을 적응적으로 찾아간다. 자극 조정 연산에서 첫번째 완전 연결 레이어는 감소율 r을 갖는 차원 감소 역할을 수행하며 두 번째 완전 연결 레이어는 특징맵의 채널 차원을 복원하는 역할을 수행한다. Sigmoid 함수를 통해 계산된 가중치들은 특징맵과의 요소별 곱셈을 통해 원래의 특징맵을 보정한다. SENET을 향상시키기 위해서는 본 논문에서는 압축 연산 부분을 강화시키는 방식을 채택하였다. 기존 SENET과는 다르게 본 논문에서는 특징맵의 선명도를 높이기 위해 영상 개선에 사용되는 대조비 펼침(Contrast stretching)^[17] 기법을 통해 가중치를 적용하는 Global Weighted Average Pooling(GWAP) 압축 연산을 적용한다. GWAP는 Eq. (4)와 같이 GAP보다 구별 가능한 채널별 통계를 포함하는 압축 연산을 수행할 수 있다.

(4)

S_{G W A P} (c) = \frac{1}{h} \sum_{i = 1}^{h} α_{c} (i) G_{\max_{c}},

여기서 $α_{c} (i) = (y_{c} (i) - G_{\min_{c}}) / (G_{\max_{c}} - G_{\min_{c}})$ 는 채널 c의 특징 함수의 대조비 펼침 변환, h는 채널 c 의 특징 길이, $G_{\max_{c}}$ 와 $G_{\min_{c}}$ 은 채널 c 특징의 최대값, 최소값을 나타낸다.

https://static.apub.kr/journalsite/sites/ask/2020-039-06/N0660390611/images/ASK_39_06_11_F2.jpg

Fig. 2

Attention based ConvNet.

https://static.apub.kr/journalsite/sites/ask/2020-039-06/N0660390611/images/ASK_39_06_11_F3.jpg

Fig. 3

SENET structure.

2.3 Long Short-Term Memory Networks

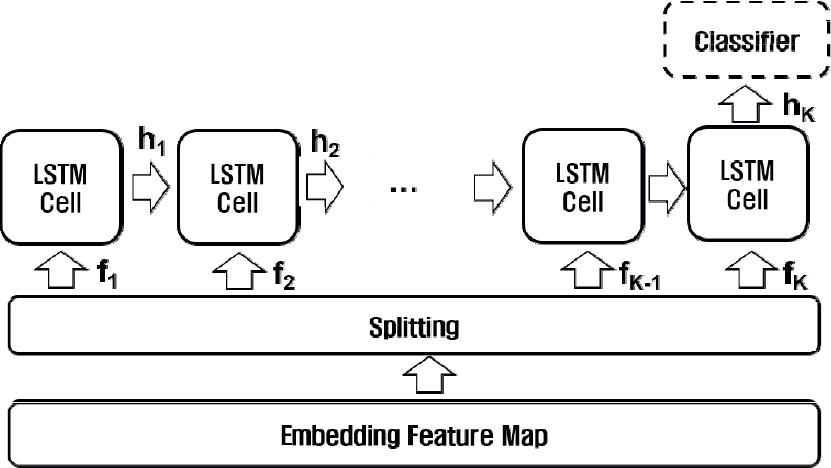
순환신경망은 과거의 상태 정보가 미래의 결과에 영향을 줄 수 있는 순환 구조를 가지고 있다. 그러나 RNN은 순차적 입력의 길이가 길어진 경우 vanishing gradient 문제가 발생하여 모델 학습이 불가능해진다. LSTM은 RNN의 개선된 모델 중 하나로 long-term dependency 문제를 완화시켜 다양한 분야의 순차적 데이터 처리 모델로 사용되고 있다. 본 논문에서는 Fig. 4와 같은 다중 순차적 데이터를 입력 받아 단일 상태를 출력하는 LSTM Net를 이용하여 지진 이벤트의 동적 특징들을 추출한다. Fig. 4에서 LSTM Net의 순차적 입력값은 ConvNet에서 추출된 Kx32 특징맵을 이용한다. Kx32 특징맵은 splitting 과정을 통해 32 차원을 가진 K 개의 순차적 특징 데이터 $f_{1}, f_{2} \dots, f_{K}$ 로 나뉘게 된다. K개의 순차적 특징 입력은 LSTM 셀의 입력값으로 사용된다. LSTM 셀은 2-레이어로 구성된 다중 레이어 셀 구조를 지니며 은닉 상태(Hidden state, h_K)의 크기는 128차원으로 설정한다. LSTM Net 모델 훈련시 과적합을 방지하기 위해 본 논문에서는 입력과 은닉 상태에 대한 dropout^[18] 훈련 방식을 적용한다.

https://static.apub.kr/journalsite/sites/ask/2020-039-06/N0660390611/images/ASK_39_06_11_F4.jpg

Fig. 4

LSTM Net.

2.4 Classifier

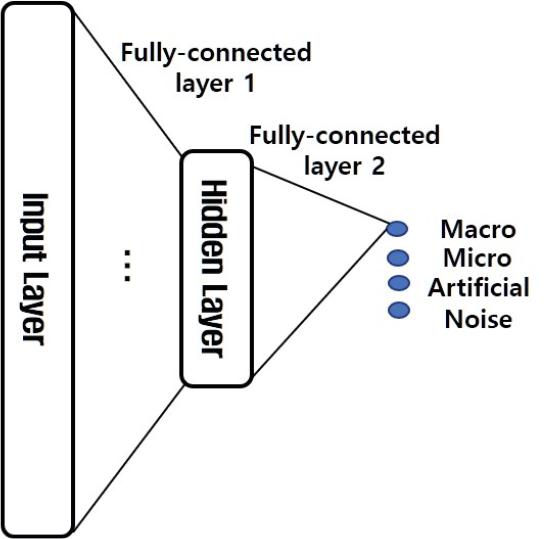
LSTM Net의 K번째 LSTM에서 추출된 은닉 상태벡터는 지진 이벤트 분류를 위한 동적 특징으로 사용된다. 동적 특징 벡터는 Fig. 5와 같은 2개의 완전 연결된 레이어와 소프트맥스 함수를 통해 지진 이벤트 분류를 수행한다. 입력 레이어는 128개의 노드로 구성되었으며 은닉 레이어는 32개의 노드로 구성한다. 최종 출력 레이어는 4종의 지진 분류 결과를 출력한다. 분류기 모델 훈련시 과적합을 방지하기 위해 첫번째 완전 연결 레이어에 dropout를 적용한다.

https://static.apub.kr/journalsite/sites/ask/2020-039-06/N0660390611/images/ASK_39_06_11_F5.jpg

Fig. 5

(Color available online) Classifier.

III. 데이터셋

본 논문에서는 2016년부터 2019년까지의 대한민국에서 발생하여 국내 관측소에서 측정한 지진 데이터와 1984년부터 2018년도까지 국외에서 발생하여 국외 관측소에서 측정한 지진 데이터베이스 STEAD를 이용하여 지진 이벤트 데이터 및 잡음 데이터를 수집하였다.^[19,20] 국내 지진데이터의 경우 기상청에서 제공되는 24 h 지진 관측 데이터 및 지진 이벤트 목록 파일을 토대로 훈련 데이터셋과(2016 ~ 2017년, 2019년) 테스트셋을(2018년도) 구성하였다. 지진 데이터는 HH 유형 속도계 센서, 100 샘플 데이터만을 이용하고 있으며 데이터베이스는 중간규모(규모 3.0 이상), 미소지진(규모 3.0 미만), 인공지진, 잡음 카테고리로 구분하였다. 훈련 및 테스트에 이용될 지진 이벤트의 수집 방식은 기본적으로 각 관측소에서 지진을 관측한 시점부터 20 s 구간의 데이터를 추출하였다. 이와 더불어 수집 데이터의 양을 늘리기 위해 각 관측소별 지진 관측 시점 보다 5 s 앞에서부터 1 s까지 1 s 간격의 sliding 방식을 적용하여 데이터를 추출 하였다. 그러나 중간 규모 지진의 경우 국내 지진 데이터가 충분하지 않았으며 STEAD 데이터셋의 국외 지진 데이터를 이용하여 부족한 훈련 및 테스트셋을 보충하였다. STEAD 데이터셋으로부터 임의 추출 방식을 통해 약 40,000개를 훈련에 사용하였으며 약 2,900개를 추출하여 테스트에 이용하였다. 잡음 이벤트의 경우 지진 이벤트 목록에 기록되지 않은 날짜에서 임의적으로 20 s 구간의 샘플을 추출하였다. 모의 실험에서 사용하는 데이터셋 구성은 Table 1과 같다.

Table 1.

Datasets.

Type	Number of training	Number of test
Macro-earthquake (Ma)	41,568 (Domestic:1,596 STEAD:39,972 )	3,000 (Domestic:96 STEAD:2,904 )
Micro-earthquake (Mi)	35,034	3,000
Artificial-earthquake (Art)	5,022	1,890
Noise (Noi)	60,000	3,000

IV. 모의 실험

4.1 실험 환경

제안한 모델의 효용성을 분석하기 위해 Table 1의 훈련 데이터셋은 학습 80 %, 검증 20 %의 비율로 사용하여 모델 학습을 수행하였다. 모델 학습에 필요한 하이퍼파라메터는 다음과 같다. 먼저 첫 번째 합성곱 레이어인 ‘Conv 1’에서는 3 × 1 필터를 간격 1로 적용하였으며 필터의 입력 채널은 3, 출력 채널은 32로 설정하였다. ‘Conv 1’ 이외의 합성곱 레이어에서도 필터 크기는 동일하지만 필터의 입력 및 출력 채널 수는 32로 설정하였다. 또한 풀링 크기는 2 × 1, 간격이 2 인 최대 풀링을 사용하였다. 주의 모듈에서 자극 조정 연산의 감소율 r 은 4로 설정하였으며 dropout 정규화에서는 뉴런을 임의로 50 % 만 사용하도록 설정하였다. 모델 최적화 기법은 ADAM 방법을 이용하였으며 학습률, L₂ 정규화 매개 변수 및 배치 크기는 각각 10^-3, 10^-5, 128로 설정하였다. 시뮬레이션은 NVIDIA Geforce GTX 1080Ti 2xGPU 및 Tensorflow에서 수행되었으며 네트워크 학습은 300번의 에포크(Epoch)를 수행하였다. 성능 측정은 Eq. (5)와 같이 정확도(Accuracy), True Positive Rate(TPR), False Positive Rate(FPR) 지수를 사용한다. 정확도는 총 테스트 개수 중에서 정확하게 추정된 결과(TP : true positive 개수, TN : true negative 개수) 개수의 비로 정의된다.

(5)

A c c u r a c y = \frac{T P + T N}{N u m b e r o f t e s t}, T P R = \frac{T P}{T P + F N}, F P R = \frac{F P}{T N + F P} .

4.2 모델에 따른 분류 성능 분석

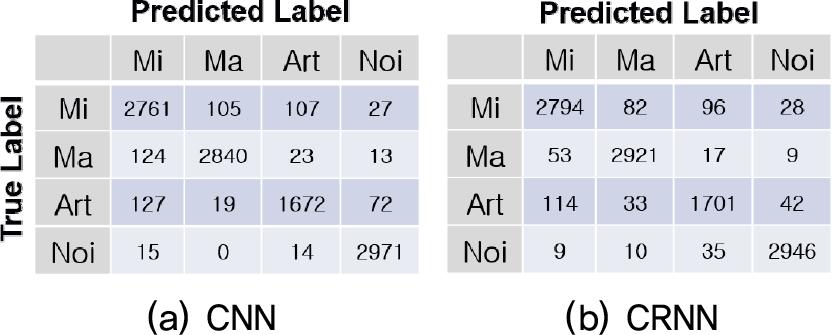
제안한 CRNN 모델의 분류 성능을 알아보기 위해 본 실험에서는 CNN 기반의 지진 분류 모델을 비교 평가 대상으로 하였다.^[6] CNN 모델과 CRNN 모델 모두 전처리를 거친 지진 데이터를 이용하여 학습 및 테스트를 진행하였다. 고주파 필터링의 차단주파수는 2 Hz로 설정하였다. Table 2는 CRNN과 CNN을 이용한 지진 이벤트 분류 성능 결과이다. Table 2에서 Mi/Ma/Art/Noi는 미소지진/중간규모지진/인공지진/잡음을 나타낸다. 전반적으로 데이터의 동적 특성을 반영한 CRNN 모델이 CNN 모델보다 우수한 성능을 보여주었으며 동적 특성 반영을 통하여 Fig. 6과 같이(인공 vs 미소) 사이의 오분류 부분이 소폭 향상되는 결과를 얻을 수 있었다. 특히 CNN 모델에서 부족했던 인공지진 분류 성능을 90 % 대까지 향상시키는 결과를 얻을 수 있었다.

Table 2.

Performance comparison of CNN and CRNN. [%]

Event	CNN			CRNN
Event	Acc	TPR	FPR	Acc	TPR	FPR
Mi/Ma/ Art/Noi	94.1	92.0	3.4	95.2	93.1	2.2
		94.7	1.6		97.4	1.6
		88.5	1.6		90.0	1.6
		99.0	1.4		98.2	1.0

https://static.apub.kr/journalsite/sites/ask/2020-039-06/N0660390611/images/ASK_39_06_11_F6.jpg

Fig. 6

(Color available online) Confusion matrix.

4.3 전처리에 따른 분류 결과 분석

Table 3은 고주파 필터 적용 유무에 따른 지진 이벤트 분류 결과이다. 저주파 대역에 존재하는 저주파 잡음 요소를 제거함으로써 전체적으로 분류 성능이 향상되는 것을 볼 수 있었다. (인공 vs 미소), (인공 vs 잡음) 사이의 오분류 부분이 전처리로 인해 줄어드는 결과를 얻을 수 있었다. 특히 인공 지진의 경우 전처리를 하게 되면 TPR이 10 % 정도 향상되는 모습을 볼 수 있었다.

Table 3.

Performance Comparison according to preprocessing. [%]

Event	0 Hz			2 Hz
Event	Acc	TPR	FPR	Acc	TPR	FPR
Mi/Ma/ Art/Noi	92.6	90.0	3.1	95.2	93.1	2.2
		99.4	2.2		97.4	1.6
		80.0	2.5		90.0	1.6
		96.5	2.2		98.2	1.0

4.4 LSTM time step에 따른 분류 결과 분석

제안한 CRNN 모델에서 embedding 특징 및 LSTM의 셀 개수는 밀접한 관련이 있다. Conv 레이어의 개수가 증가할 수록 LSTM 셀의 개수는 줄어드는 역관계를 가진다. 본 실험에서는 LSTM의 셀 개수를 125 (Conv 레이어 4개 적용), 63(Conv 레이어 5개 적용)로 변화해 가며 분류 성능 결과를 알아보았다. Table 4는 각 설정에 따른 지진 이벤트 분류 성능 결과이다. 모든 이벤트의 분류 성능을 고려할 때 LSTM의 개수가 125인 모델이 LSTM 개수가 63인 모델보다 우수한 성능을 나타내었다.

Table 4.

Performance comparison according to time step. [%]

Event	63 (Conv 5)			125 (Conv 4)
Event	Acc	TPR	FPR	Acc	TPR	FPR
Mi/Ma/ Art/Noi	94.9	95.3	3.8	95.2	93.1	2.2
		94.6	1.0		97.4	1.6
		88.1	1.0		90.0	1.6
		99.1	1.3		98.2	1.0

V. 결 론

본 논문에서는 다양한 지진 이벤트 분류를 위한 CRNN 모델을 제안하였다. 지진 파형의 정적 특성과 더불어 동적 특성을 반영하기 위해 적합한 ConvNet과 LSTM Net를 순차적으로 사용하는 구조를 적용하였으며 전체 모델의 안정적인 학습을 위해서 배치정규화 및 dropout 기법이 적용되었다. 또한 정적인 특징을 보다 세밀하게 추출하기 위해 주의 모듈이 적용된 ConvNet 구조를 제안하였다. 제안된 CRNN 구조는 기존의 CNN 구조보다 향상된 분류 성능을 보여 주었으며 동적 특성을 통하여 지진 이벤트 사이의 오분류를 감소시키는 결과를 얻을 수 있었다. 또한 전처리 적용을 통해서 오분류가 발생했던 부분들이 감소되는 모습을 확인할 수 있었으며 전처리 비사용 모델에 비해 안정적인 분류 성능 결과를 얻을 수 있었다.

Acknowledgements

본 논문은 기상청 기상/지진 See-At 기술개발연구 사업 ‘인공지능 기술 활용 지진감지업무 적용 기술 연구’의 연구결과 중 일부이다(KMI2018-09610).

References

H. I. Fawaz, G. Forestier, J. Weber, L. Idoumghar, and P.-A. Muller, "Deep learning for time series classification: a review," arXiv: 1809.04356 (2018).

Z. Cui, W. Chen, and Y. Chen, "Multi-scale convolutional neural networks for time series classification," arXiv:1603.06995 (2016).

J. Lee, J. Park, K. L. Kim, and J. Nam, "SampleCNN : End-to-end deep convolutional neural networks using very small filter for music classifications," Applied Science, 8, 150 (2018). 10.3390/app8010150

X. Zeng, D. Zhou, and X. Zeng, "HeartID: A multiresolution convolutional neural network for ECG- based biometric human identification in smart health applications," IEEE Access, 5, 11805-11816 (2017). 10.1109/ACCESS.2017.2707460

K. Choi, G. Fazekas, M. Sandler, and K. Cho, "Convolutional recurrent neural networks for music classification," arXiv:1609.04243v3 (2016). 10.1109/ICASSP.2017.7952585

B. Ku, J. Min, J.-K. Ahn, J. Lee, and H. Ko, "Earthquake event classification using multitasking deep learning," IEEE Geoscience and Remote Sensing Letters, early access, 1-5 (2020). 10.1109/LGRS.2020.2996640

M. Withers, R. Aster, C. Young, J. Beiriger, M. Harris, S. Moore, and J. Trujillo, "A comparison of select trigger algorithms for automated global seismic phase and event detection," Bull. Seismol. Soc. Am. 88, 95-106, (1998).

S. J. Gibbons and F. Ringdal, "The detection of low magnitude seismic events using array-based waveform correlation," Geophys. J. Int. 165, 149-166 (2006). 10.1111/j.1365-246X.2006.02865.x

J. Skoumal, M. R. Brudzinski, B. S. Currie, and J. Levy, "Optimizing multi-station earthquake template matching through re-examination of the Youngstown, Ohio, sequence," Earth and Planet Science Letters, 405, 274-280 (2014). 10.1016/j.epsl.2014.08.033

C. E. Yoon, O. O'Reilly, P. J. Bergen, and G. C. Beroza, "Earthquake detection through computationally efficient similarity search," Science Advances, 1, e1501057 (2015). 10.1126/sciadv.150105726665176PMC4672764

T. Perol, M. Gharbi, and M. Denolle, "Convolutional neural network for earthquake detection and location," Science Advances, 4, e1700578 (2018). 10.1126/sciadv.170057829487899PMC5817932

S. M. Mousavi, W. Zhu, Y. Sheng, and G. C. Beroza, "CRED: A deep residual network of convolutional and recurrent units for earthquake signal detection," arXiv:1810.01965 (2018). 10.1038/s41598-019-45748-131311942PMC6635521

A. Mignan and M. Broccardo, "Neural network applications in earthquake prediction (1994-2019): Meta- analytic insight on their limitations," arXiv:1910.011 78 [cs.NE] (2019). 10.5194/egusphere-egu2020-6851

J. Hu, L. Shen, S. Albanie, G. Sun, and E. Wuf, "Squeeze-and-excitation networks," arXiv:1709.01507 (2017).

S. Hochreiter and J. Schmidhuber, "Long short-term memory," Neural Computation, 9, 1735-1780 (1997). 10.1162/neco.1997.9.8.17359377276

S. Ioffe and C. Szegedy, "Batch normalization: Accelerating deep network training by reducing internal covariate shift," arXiv:1502.03167 (2015).

R. E. Woods and R. C. Gonzalez, Digital Image Processing (Pearson, New York, 2018), pp. 129-130.

N. Srivastava, G. Hinton, A. Krizhevsky, I. Sutskever, and R. Salakhutdinov, "Dropout: A simple way to prevent neural networks from overfitting," J. Machine Learning Research, 15, 1929-1958 (2014).

NECIS, http://necis.kma.go.kr//, (Last viewed March 31, 2020).

S. M. Mousavi, Y. Sheng, W. Zhu, and G. C. Beroza, "STanford EArthquake Dataset (STEAD): A global data set of seismic signals for AI," IEEE Access, 7, 179464-179476 (2019). 10.1109/ACCESS.2019.2947848

The Journal of the Acoustical Society of Korea ISSN:1225-4428(Print) 2287-3775(Online) 한국음향학회지

Preview

Earthquake events classification using convolutional recurrent neural network

ABSTRACT

MAIN

Fig. 1

(Color available online) Proposed CRNN structure.

(1)

(2)

(3)

(4)

Fig. 2

Attention based ConvNet.

Fig. 3

SENET structure.

Fig. 4

LSTM Net.

Fig. 5

(Color available online) Classifier.

Table 1.

Datasets.

(5)

Table 2.

Performance comparison of CNN and CRNN. [%]

Fig. 6

(Color available online) Confusion matrix.

Table 3.

Performance Comparison according to preprocessing. [%]

Table 4.

Performance comparison according to time step. [%]

Acknowledgements

References