I. 서 론
수중에서 발생하는 인위적인 소음으로 인한 해양 생태계 변화가 지속적으로 발생하고 있다. 이에 따라 International Fund for Animal Welfare(IFAW)[1]를 비롯한 해양환경 보호단체에서 인위적 수중소음에 의한 해양생물 피해를 연구하여 국제적인 규정 제정을 촉구하고 있다. 대표적인 인위적 수중소음으로써 해양구조물의 설치/운용/해체 및 선박의 운항 시 발생하는 소음을 들 수 있다.[2]
인위적 소음원에 의한 수중소음 감소를 위해 기포의 음향감쇠 특성이 활용되고 있다. 해양구조물의 파일링 작업 시 발생하는 충격파의 수중 전파를 막기 위해 파일 주위에 기포커튼을 설치하는 방안이 연구되었고,[3] 함정의 경우 선박 내부 기계류에 의한 진동이 선체를 통해 수중으로 전파하는 것을 막기 위해 선체 표면을 따라 기포층을 형성하는 에어마스커 시스템이 적용되기도 하였다.[4] 이러한 방법들에 의한 음향 감쇠 효과를 평가하는 척도로서 삽입손실이 주로 사용된다. 삽입손실은 기포층이 없을 때와 있을 때의 원거리 음향장의 크기 비로 정의되는데, 소기의 소음감소 목표달성을 위해 사전에 삽입손실을 추정하는 것이 중요하다.
기포층의 활용과 유사하게 특정 위치 또는 특정 주파수 대역에서 유동소음 및 구조소음 저감을 위해 음향 배플이 활용되기도 한다. Ko et al.[5]은 탄성 구조체와 다양한 음향 배플의 조합에 대해 소음 감소량을 계산한 바 있다. 이 때 소음감소 성능은 음향 배플의 임피던스와 층의 두께에 의해 결정되며, 배플의 임피던스는 실수 값을 갖는다. 한편, Foldy[6]에 의하면 군집을 이루는 기포 내에서 전파하는 음파의 평균 음압은 파동방정식을 따르며, 이 때 음속은 기포가 없을 때 매질의 음속과는 달리 복소수 형태의 값을 보인다. 따라서 기포층을 기포 분포특성에 따른 음속(또는 임피던스)의 유효매질(effective medium)로 가정한다면, Ko et al.[5]이 제시한 기법의 적용이 가능하다. Commander와 Prosperetti[7]는 유효매질 기법을 이용하여 얇은 기포층에서의 투과/반사 계수를 제시하였다. Junger와 Cole[8]은 ‘진공-평판-기포층-유체’ 모델에서 평판의 한 점에서 진동할 때 기포층에 의한 삽입손실 해석해를 제시한 바 있다.
기포커튼의 경우 수층에서의 음장의 크기를 직접적으로 예측하여 기포층의 효과를 분석하기도 하였다. Göttsche et al.[9]은 파일링 충격에 의한 근거리 음장을 유한요소법을 통해 추정한 후 이를 일종의 가상음원으로 치환하였고 포물선 방정식법을 이용한 음전달 기법을 통해 수층에서의 음장을 추정하였다. 이 때, 기포층은 복소수 음속을 갖는 유효매질로 치환하였다. Tsouvalas와 Metrikine[10]은 파일의 거동과 수층의 음장을 모드해석을 통해 구하는 반 해석적 모델(semi-analytical model)을 제안하였다. Tsouvalas와 Metrikine 모델 또한 기포층을 유효매질로 간주하였다. 한편, Tsouvalas와 Metrikine는 기포율, 기포층 두께, 기포커튼 위치, 파일의 직경 등의 파라미터 연구를 통해 저주파 대역에서는 기포층과 수층의 임피던스 불일치로 인한 음파의 차단이 주요한 소음저감 메커니즘이고 고주파 대역에서는 기포층에서의 감쇠가 소음저감의 주된 원인임을 보였다. Rustemeier et al.[11]은 다양한 기포 크기와 기포율의 기포커튼들에 대해 실험실 규모의 실험과 호수 실험을 각각 수행하였고 호수 계측 결과를 해석해와 비교하였다. Rustemeier et al.은 해석해를 유효매질(기포층)의 음향댐핑으로 정의하였으나, 그들의 해석해에는 Tsouvalas와 Metrikine[10]이 지적한 바와 같이 주파대역에서 중요한 기포층에서의 반사효과가 고려되지 않았다.
본 연구에서는 Ko et al.[5]이 제시한 유도 방식을 따라 ‘유체-기포층-유체’ 모델의 기포커튼에 의한 삽입손실 해석해를 유도하였고, 수치모의를 통해 평균 반지름 1.5 mm의 기포들로 구성된 기포층의 두께 및 기포율에 따른 삽입손실의 거동을 고찰하였다. 또한 Junger와 Cole[8]의 모델을 ‘진공-평판-유체-기포층-유체’ 모델로 확장한 에어마스커의 삽입손실 해석해를 유도하였고, 수치모의를 통해 평판과 기포층의 거리에 따른 영향을 중심으로 삽입손실의 특성을 살펴보았다. 본 논문에서 제시된 삽입손실 해석해에는 임피던스 차이에 기인한 기포층에서의 반사효과와 감쇠가 모두 고려되었다.
II. 유효매질 이론
기포와 유체가 혼합된 매질의 위치 에서 반지름이 ~ 에 속하는 기포의 단위부피당 평균 개수를 라 하자. 이 때, 는 기포의 분포함수이며 부피 에 대해 전체 기포의 수 은 이 된다. 또한 혼합매질에서 기포율 은 이다.
전체 매질에서 한 개의 기포만 있는 경우, 입사파 에 의해 기포의 표면으로부터 생성된 구면파 형태의 산란파의 크기는 입사파의 크기에 비례하며, 기포의 주파수()와 크기()에 의해 결정되는 산란특성에 따라 달라진다. 따라서 기포의 위치와 수음점의 위치를 각각 와 라 할 때, 수음점에서의 산란장()은 다음과 같이 표현된다.
| $$p_s(\vec r;\vec{r_0},a)=p_i(\vec{r_0})s(\vec{r_0},a)\frac{e^{i(k_0\vert\vec r-\vec{r_0}\vert R)}}{\vert\vec r-\vec{r_0}\vert}.$$ | (1) |
Eq. (1)에서 는 기포가 없는 유체 매질에서의 파수를 의미하며, 기포의 산란함수 는 다음과 같이 유도된다.[2]
| $$s(\vec r,a)=\frac{a(\vec r)}{(w_R/w)^2-1+i\delta}.$$ | (2) |
Eq. (2)에서 은 기포의 공진 주파수이고, 는 기포의 댐핑상수를 의미한다.
한편, 기포들 사이의 다중 산란을 무시할 수 있을 정도로 기포가 희박하게 분포하고 있는 상태를 가정했을 때 기포 군집에서 입사파 에 의한 전체 음장(total field) 은 다음과 같이 입사파와 여러 기포로부터 산란된 음장들의 합으로 표현될 수 있다.
| $$p(\vec r)=p_i(\vec r)+\sum_{j=1}^Ns(\vec{r_j})p_e(\vec{r_j})\frac{e^{i(k_0\vert\vec r-\vec{r_j}\vert)}}{\vert\vec r-\vec{r_j}\vert}.$$ | (3) |
Eq. (3)에서 는 번째 기포에 입사된 모든 음장의 합, 즉 외부 음장(external field)을 의미하며 다음과 같이 입사파와 해당 기포를 제외한 주변의 기포들로부터 산란된 산란장의 합으로 정의된다.
| $$p_e(\vec{r_j})=p_i(\vec{r_j})+\sum_{k=1,(k\neq j)}^Ns(\vec{r_k})p_e(\vec{r_k})\frac{e^{i(k_0\vert\vec{r_j}-\vec{r_k}\vert)}}{\vert\vec{r_j}-\vec{r_k}\vert}.$$ | (4) |
확률변수로써 모든 기포의 위치 과 크기 는 서로 독립이라 가정할 때, 체적 에서 기포의 평균 전체 음장 은 다음과 같이 유도될 수 있다.
| $$\left\langle p(\vec r)\right\rangle=p_i(\vec r)+\int_V^{}{S(\vec{r_j})\left\langle p_e(\vec{r_j})\right\rangle^{(j)}\frac{e^{i(k_0\vert\vec{R_j}\vert)}}{\vert\vec{R_j}\vert}}d\vec{r_j}.$$ | (5) |
Eq. (5)에서 는 기포 를 제외한 나머지 기포들의 위치 평균을 의미하고 는 를 뜻한다. 또한 는 전체 산란함수로써 다음과 같이 정의된다.
| $$S(\vec r)=\int_0^\infty{s(\vec r,a)ada}.$$ | (6) |
Eqs. (3)과 (4)를 비교할 때, Eq. (5)의 는 로 근사할 수 있고, 이 때 근사오차는 로써 기포의 개수가 늘어날수록 근사오차는 줄어들 것이다. 따라서 Eq. (5)는 다음과 같이 적분방정식으로 근사된다.
| $$\left\langle p(\vec r)\right\rangle=p_i(\vec r)+\int_V^{}{S(\vec{r_0})\left\langle p(\vec{r_0})\right\rangle\frac{e^{i(k_0\vert\vec{R_0}\vert)}}{\vert\vec{R_0}\vert}}d\vec{r_0}.$$ | (7) |
Eq. (7)의 양 변에 연산자 []를 적용하면 다음과 같은 방정식을 얻을 수 있다.
| $$\nabla^2\left\langle p(\vec r)\right\rangle+\lbrack k_0^2+4\pi S(\vec r)\rbrack\left\langle p(\vec r)\right\rangle=0.$$ | (8) |
Eq. (8)에서 로부터 은 전파 특성이 기포의 분포와 산란에 의해 결정되는 매질에서의 파동방정식의 해가 됨을 알 수 있다. 이러한 매질을 유효매질이라 하며, 유효매질에서 파수 는 의 관계로부터 구할 수 있고, 허수부의 부호는 일 때 해가 발산하지 않도록 결정된다.
III. 삽입손실
3.1 기포커튼 삽입손실
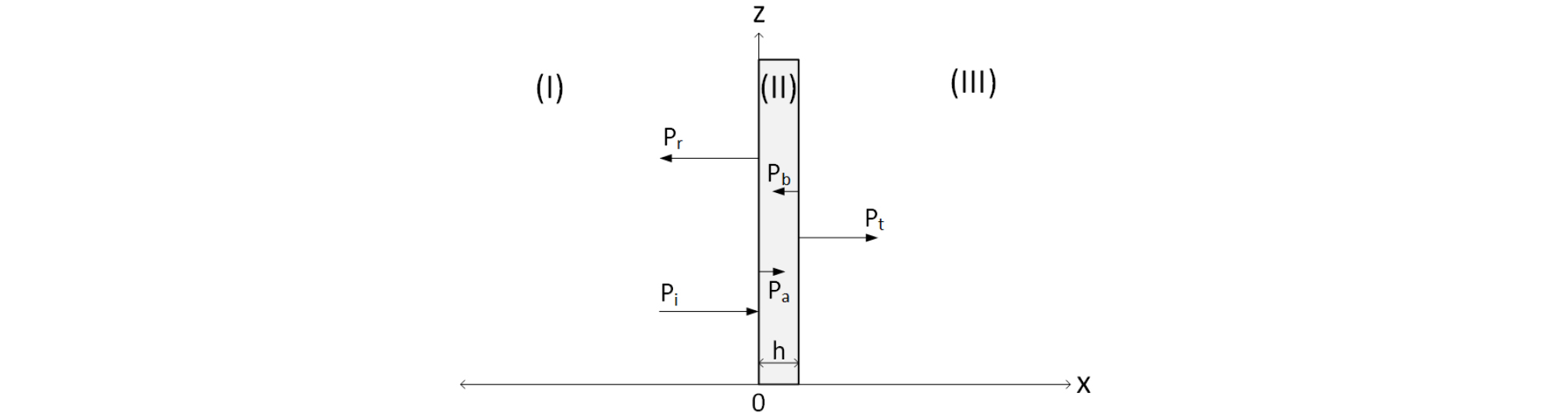
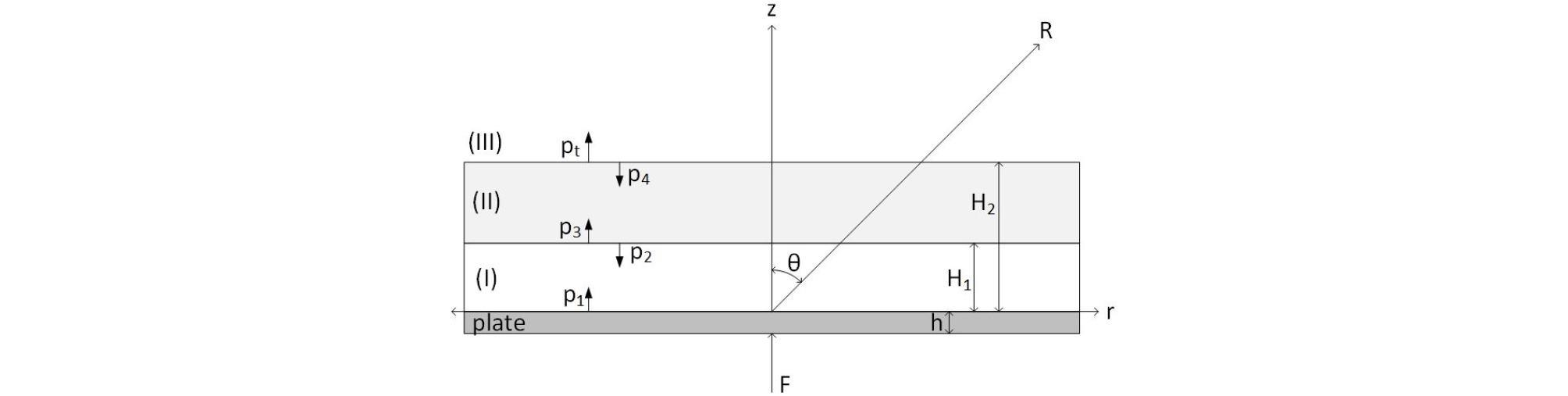
기포커튼은 해양 구조물 설치 등을 위한 파일링 작업 시 발생하는 충격파를 감소시키기 위해 파일을 중심으로 동심원 형태로 설치된 기포층을 의미한다. 기포커튼이 음원으로부터 충분한 거리에 위치해 있을 때 기포층에 도달한 음파는 평면파로 가정할 수 있다. Fig. 1과 같이 기포층에 평면파()가 입사할 때, 두께 인 기포층으로부터 반사파()와 기포층을 통과한 투과파()가 존재한다. 또한 기포층 내부에서도 투과파()와 반사파()가 생성된다. 전파방향을 고려한 매질 (I)에서 주파수 일 때 음파는 다음과 같이 표현된다.
| $$p_i=P_ie^{-i(wt-k_wx)},$$ | (9.a) |
| $$p_r=P_re^{-i(wt+k_wx)}.$$ | (9.b) |
위 식에서 은 수층에서의 파수로써 수층의 음속을 라 할 때 의 관계가 있다. 마찬가지로 매질 (II)와 매질 (III)에서의 음파도 다음과 같이 표현된다.
| $$p_a=P_ae^{-i(wt-k_ex)},$$ | (9.c) |
| $$p_b=P_be^{-i(wt+k_ex)},$$ | (9.d) |
| $$p_t=P_te^{-i(wt-k_wx)}.$$ | (9.e) |
Eqs. (9.c)과 (9.d)에서 는 기포층의 유효파수를 의미한다.
기포층과 수층의 경계(Fig. 1에서 )에서 두 매질의 압력과 속도는 연속이어야 하므로 만족해야 할 경계조건은 다음과 같다.
| $$P_i+P_r=P_a+P_b,$$ | (10.a) |
| $$P_ae^{ik_eh}+P_be^{-ik_eh}=P_te^{ik_wh},$$ | (10.b) |
| $$\frac1{Z_w}(P_i-P_r)=\frac1{Z_e}(P_a-P_b),$$ | (10.c) |
| $$\frac1{Z_e}(P_ae^{ik_eh}-P_be^{-ik_eh})=\frac1{Z_w}P_te^{ik_wh}.$$ | (10.d) |
Eqs. (10.c)와 (10.d)에서 는 수층의 임피던스로서 수층의 밀도가 일 때 가 된다. 기포층의 임피던스는 가 되며, 기포의 밀도가 일 때 유효밀도 는 가 된다. 또한 유효음속 는 이다.
Eqs. (10.a) ~ (10.d)로부터 다음과 같이 를 구할 수 있다.
| $$P_t=\frac{2P_ie^{-ik_wh}}{2\cos(k_eh)-i(Z_w/Z_e+Z_e/Z_w)\sin(k_eh)}.$$ | (11) |
이상으로부터 기포 스크린에 의한 삽입손실 은 로 계산될 수 있다.
삽입손실에서 기포층의 두께와 기포율의 영향을 살펴보기 위해 수치모의를 수행하였다. 수치모의에 사용된 환경인자는 Table 1과 같다. 기포의 분포는 평균 1.5 mm, 표준편차 0.3 mm의 표준정규분포를 기반으로 해당 기포율에 따라 설정하였다.
Table 1.
Parameters for bubble curtain simulation.
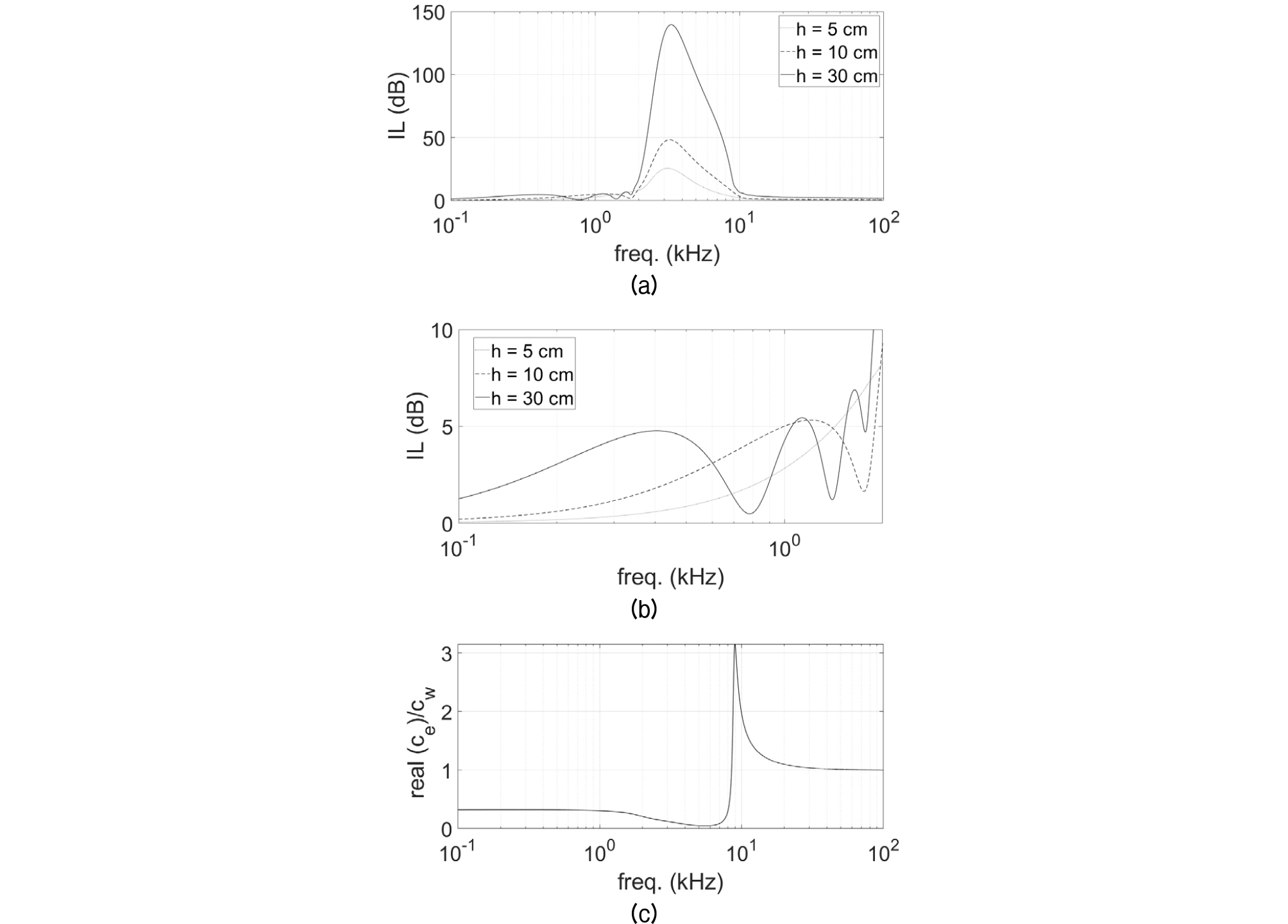
Fig. 2는 기포층 두께 별 삽입손실과 수층의 음속대비 기포층의 유효음속(위상 속도)비를 보여준다. 이 때 기포층의 기포율은 0.001이다. Fig. 2(a)로부터 기포층의 두께가 두꺼워질수록 삽입손실이 급격히 증가하는 것을 알 수 있다. 한편, Fig. 2(b)로부터 저주파 영역(kHz)에서는 삽입손실의 모드 특성을 확인할 수 있다. 주파수 2 kHz 기준 기포층의 음속이 약 480 m/s이고 해당 파장이 약 24 cm이므로 10 cm 이하의 두께에서는 모드가 형성되지 않음을 알 수 있다. 2 kHz이후 주파수가 증가함에 따라 삽입손실은 증가하다가 최대점을 지나 다시 감소하는 경향을 보이며, 이 때 기포층의 유효음속은 지속적으로 작아지는 것을 볼 수 있다. 그러나 특정 주파수 근처(~9 kHz)에서 유효음속은 급속히 빨라져서 수층의 음속보다 커졌다가 다시 느려지면서 수층의 음속으로 수렴하는 현상이 발생함을 확인할 수 있다. 이러한 주파수를 반공진 주파수(anti-resonance frequency)라 하며, 반공진 주파수 대역에서 기포층에 의한 삽입손실은 급속히 줄어드는 것을 알 수 있다 .
Fig. 3(a)와 Fig. 3(b)는 기포율 변화에 따른 삽입손실과 수층의 음속대비 기포층의 유효음속 비를 각각 보여준다. 이 때 기포층의 두께는 10 cm이다. Fig. 3(a)와 Fig. 3(b)로부터 기포율이 증가할수록 삽입손실은 증가하고, 반공진 주파수 이하의 저주파 대역에서의 기포층 유효음속은 작아지는 것을 확인할 수 있다. 또한 기포율이 증가함에 따라 2 kHz 이하의 주파수 대역에서 모드 형성이 뚜렷해지는데, 이는 유효음속의 감소에 따른 것임을 알 수 있다. 반공진 주파수는 기포율에 비례하여 커졌고, Fig. 2에서와 마찬가지로 반공진 주파수 대역에서 삽입손실은 급속히 줄어드는 것을 확인하였다.
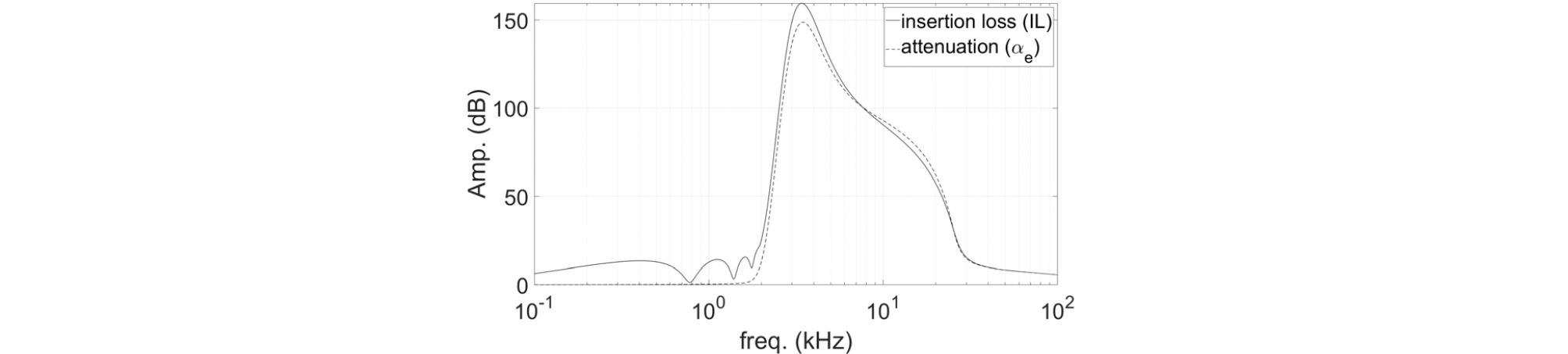
Fig. 4는 기포가 층을 형성한 경우의 삽입손실과 매질 전체가 기포와 물의 혼합물로 구성된 경우, 기포층의 두께에 해당하는 거리만큼 음파가 전파했을 때 감쇠량을 서로 비교하여 보여준다. 모의에 사용된 기포층의 두께(h)와 기포율은 가각 10 cm와 0.01이다. 기포와 물의 혼합매질에서 감쇠계수는 [nepers/m]이므로 거리 h를 전파하였을 때 감쇠량은 [dB]이 된다. 2 kHz 이내의 주파수 대역에서 감쇠량은 모드특성을 보이지 않고 그 값 또한 삽입손실보다 작게 추정되었다. 중간 주파수 대역(2 kHz ~ 24 kHz)에서 삽입손실과 감쇠량은 최대 삽입손실 대비 9.2 % 이내의 차이를 보였으며, 반공진 주파수(24 kHz)이후에서는 거의 일치하였다. 끝으로, 논문에서 결과가 그래프로 제시되진 않았지만 기포의 두께를 1 m로 늘리면 최대 삽입손실 대비 감쇠량의 차이는 1 % 이내로 줄어드는 것을 확인하였다.
3.2 에어마스커 삽입손실
선박의 엔진 등 기계류에 의한 진동이 선각에 전달되어 수중으로 전파되는 소음을 줄이기 위해 선체 외부에 인위적으로 기포층을 형성시킨다. 이를 에어마스커라 하며 최근 해양생태계 보호를 위한 선박 수중방사소음 감소기술로서 주목받고 있다.[4] 공기 분사 압력과 선체 주변의 유동장 등 여러 조건에 의해 기포층이 선체로부터 떨어져 형성될 수 있다. 따라서 본 연구에서는 Fig. 5와 같이 선체와 기포층 사이에 유체가 존재하는 일반적인 모델에 대해 기포층에 의한 삽입손실 계산식을 유도하고자 한다.
Fig. 5와 같이 실린더 좌표계의 원점에 의 힘이 작용할 때, 매질 (I), (II), (III)에서의 압력은 다음의 파동방정식을 만족해야 한다.
| $$(\nabla^2+\frac{\partial^2}{\partial z^2}+k_1^2)p(r,z)=0,0<z<H_1,$$ | (12.a) |
| $$(\nabla^2+\frac{\partial^2}{\partial z^2}+k_2^2)p(r,z)=0,H_1<z<H_2,$$ | (12.b) |
| $$(\nabla^2+\frac{\partial^2}{\partial z^2}+k_3^2)p(r,z)=0,H_2<z.$$ | (12.c) |
단, 이다. 또한, 위 식과 향후 전개될 수식에서 각 매질의 물성치(음속, 밀도)와 파수는 아래첨자의 기호 및 번호로 구별된다. 한편, 평판의 댐핑을 무시했을 때 평판의 수직변위 에 대한 운동방정식은 다음과 같다.
| $$D\nabla^2(\nabla^2\omega)+\mu\frac{d^2\omega}{dt^2}=-p_1(r,0)-p_2(r,0)+\frac F{2\pi r}\delta(r).$$ | (13) |
Eq. (13)에서 평판의 굽힘강성 는 으로 정의되며, 와 는 각각 평판의 영률과 포아송비를 의미한다. 또한 는 평판의 단위면적당 질량으로써 이고 는 Dirac 델타함수이다. 이 때 매질의 각각의 경계에서 경계조건은 다음과 같다.
| $$\frac{d^2\omega}{dt^2}=-\frac1{\rho_1}\left(\frac{\partial p_1}{\partial z}+\frac{\partial p_2}{\partial z}\right)=0,\;z=0,$$ | (14.a) |
| $$p_1+p_2=p_3+p_4,\;z=H_1,$$ | (14.b) |
| $$\frac1{\rho_1}(\frac{\partial p_1}{\partial z}+\frac{\partial p_2}{\partial z})=\frac1{\rho_2}(\frac{\partial p_3}{\partial z}+\frac{\partial p_4}{\partial z}),\;z=H_1,$$ | (14.c) |
| $$p_3+p_4=p_t,\;z=H_2,$$ | (14.d) |
| $$\frac1{\rho_2}(\frac{\partial p_3}{\partial z}+\frac{\partial p_4}{\partial z})=\frac1{\rho_3}\frac{\partial p_t}{\partial z},\;z=H_2.$$ | (14.e) |
이상의 지배방정식과 경계조건으로부터 해를 구하기 위해 다음과 같이 정의된 Hankel 변환을 이용한다.
| $$\overline\Phi(k,z)=\int_0^\infty{\Phi(r,z)J_0(kr)rdr,}$$ | (15.a) |
| $$\Phi(r,z)=\int_0^\infty{\overline\Phi(k,z)J_0(kr)kdk}.$$ | (15.b) |
Eq. (15.a)를 Eqs. (12.a) ~ (12.c)에 대입한 후 변환된 1차 미분방정식의 해는 다음과 같은 형태로 구할 수 있다.
| $$\overline p(k,z)={\overline p}_1(k,z)+{\overline p}_2(k,z)=T_1e^{i\sqrt{k_1^2-k^2}z}+R_1e^{-i\sqrt{k_1^2-k^2}z},0<z<H_1,$$ | (16.a) |
| $$\overline p(k,z)={\overline p}_3(k,z)+{\overline p}_4(k,z)=T_2e^{i\sqrt{k_2^2-k^2}z}+R_2e^{-i\sqrt{k_2^2-k^2}z},H_1<z<H_2,$$ | (16.b) |
| $$\overline p(k,z)={\overline p}_t(k,z)=T_3e^{i\sqrt{k_3^2-k^2}z},H_2<z.$$ | (16.c) |
마찬가지로 Eq. (15.a)를 Eq. (13)과 Eqs. (14.a) ~ (14.e)에 대입한 후 Eqs. (16.a) ~ (16.c)를 이용하여 정리하면 다음의 행렬식으로 얻을 수 있다.
위 식에서 와 는 각각 매질의 임피던스와 위상을 의미한다. 한편, 각 매질 와 의 경계에서 반사계수 를 도입하면 는 다음과 같이 구해진다.
Eqs. (16.c)와 (18)을 Eq. (15.b)에 대입 후 복소 영역의 경로적분으로 변환 하면 매질 (III)에서의 음압은 다음과 같다.
| $$p_t(r,z)=\frac12\oint_C^{}{T_3(k)e^{i\sqrt{k_3^2-k^2}z}H_0^{(1)}(kr)kdk}.$$ | (19) |
Eq. (19)에서 에서 해가 수렴하기 위해서는 의 허수부가 0보다 커야하며, 이에 해당하는 경로 는 에서 원점까지는 실수축의 상단을 지나고 원점에서 까지는 실수축의 하단을 지난다. 한편, 로 변환하고 Hankel 함수의 원거리() 근사식 과 그리고 임을 이용하면 Eq. (19)는 다음과 같이 변환된다.
| $$p_t(r,z)=\frac{k_3^{3/2}e^{-4i/\pi}}{\sqrt{2\pi r}}\oint_{C'}^{}{T_3(\psi)e^{ik_3Rcos(\theta-\psi)}\cos\psi\sqrt{\sin\psi}d\psi}.$$ | (20) |
Brekhovskikh[12]에 의하면 Eq. (20)의 적분은 최급강하법(method of steepest descent)으로 다음과 같이 안장점 (saddle point) 에서의 함수값으로 근사할 수 있다.
| $$p_t(r,z)=-ik_3T_3\cos\theta\frac{e^{ik_3R}}R.$$ | (21) |
삽입손실을 추정하기 위해서는 기포층이 없을 때 평판 가진에 의한 음장()을 구해야 한다. 앞서 유도된 수식들에서 으로 설정하면 는 다음과 같이 유도된다.
| $$p_0(r,z)=\frac{-iFk_3\cos\theta}{(1+Z_p/Z_3)}\frac{e^{ik_3R}}{2\pi R}.$$ | (22) |
따라서 삽입손실은 다음과 같다.
| $$IL=-20\log_{10}(\vert p_3/p_0\vert)=20\log_{10}(\frac{2Z_3}{(Z_p+Z_3)\overline{T_3}}).$$ | (23) |
앞 절에서 기포층의 두께와 기포율의 영향을 살펴보았다. 비록 수중음향의 방사 메커니즘이 다를지라도 에어마스커의 기포층에 의한 삽입손실 특성은 기포커튼의 경우와 크게 다르지 않다. 따라서 본 절에서는 기포층이 선체로부터 떨어져 형성된 경우 기포층과 선체와의 거리에 따른 영향을 중심으로 살펴보기 위해 수치모의를 수행하였다: 수치모의에 사용된 환경인자는 Table 2와 같고 기포의 분포는 기포커튼의 경우와 동일한 방식으로 설정하였다.
Table 2.
Parameters for air masker simulation.
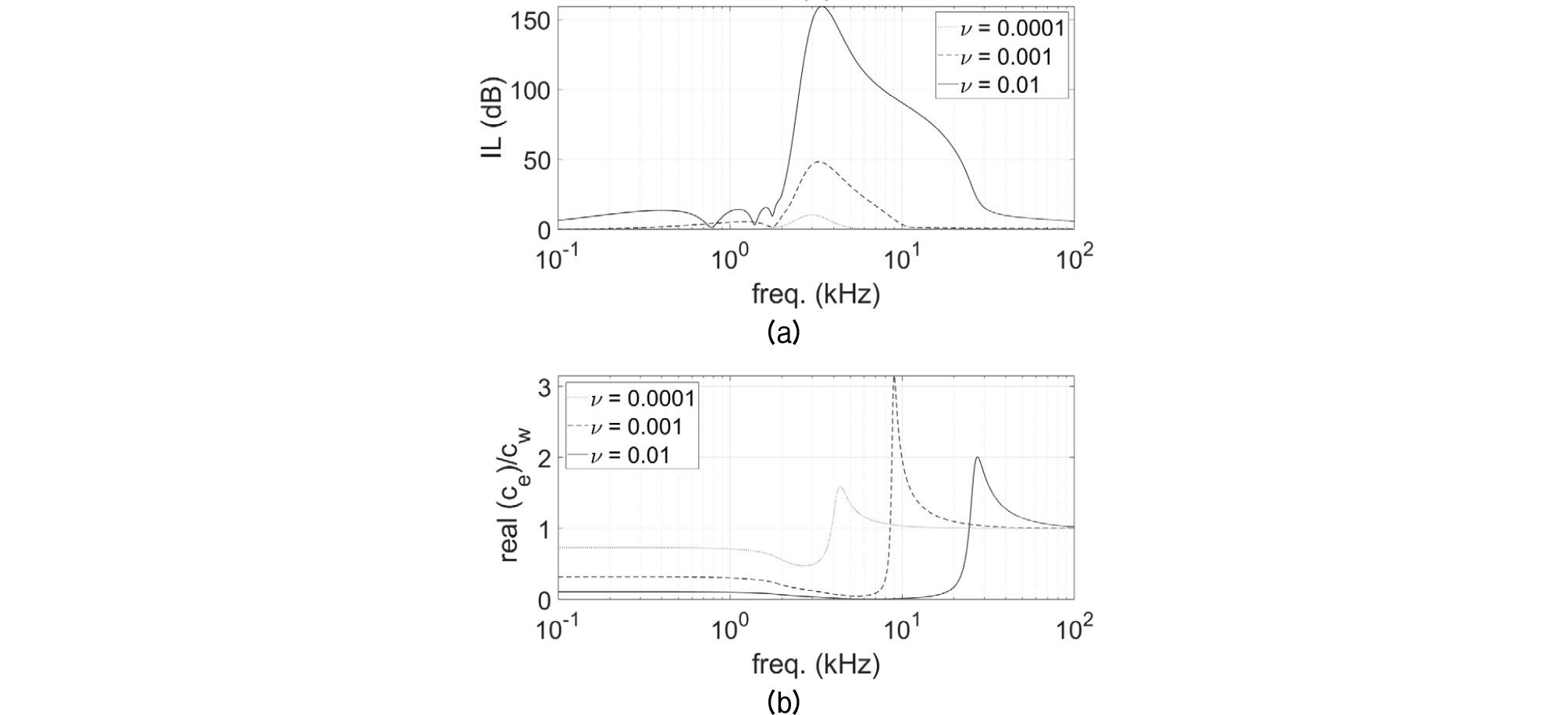
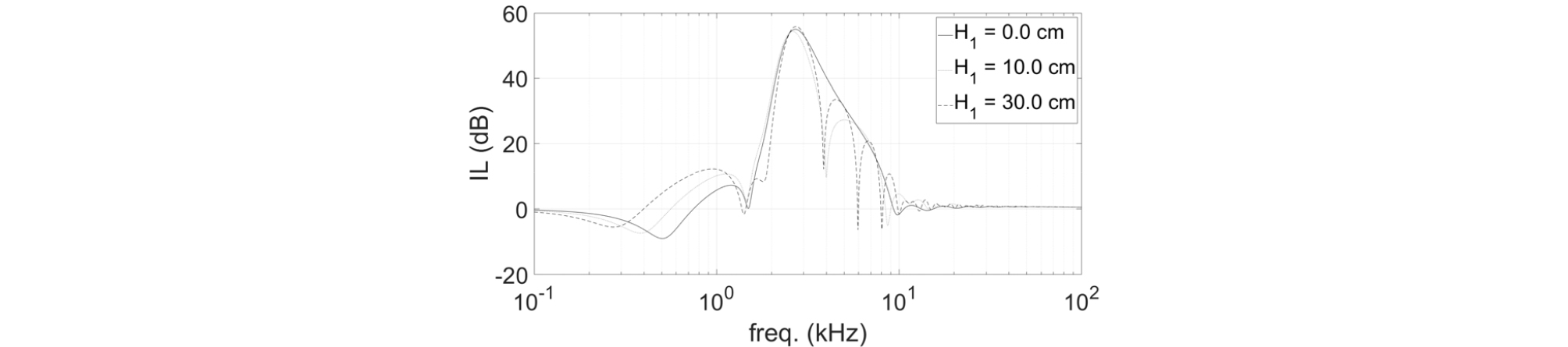
Fig. 6은 선체와 기포층의 간격이 각각 0 cm, 10 cm, 30 cm일 때 삽입손실을 보여준다. 이 때 기포층의 두께는 10 cm이고 기포율은 0.001이다. 2 kHz 이하의 저주파대역과 반공진 주파수(9 kHz) 이상의 고주파 대역의 특성은 기포커튼의 경우와 유사하다. 다만, 저주파 대역의 모드는 선체와 기포층의 간격에 따라 서로 다른 형태를 보인다. 또한 음의 값을 갖는 영역이 존재하는데, 이러한 주파수 영역에서는 기포층으로 인해 오히려 소음이 증가한다는 것을 의미한다. 감쇠가 주로 발생한 주파수 대역(2 kHz 9 kHz)에서 선체와 기포층이 떨어져 있는 경우 중간의 유체층에 의한 모드 현상이 발생하였고, 유체층의 두꺼울수록 더욱 복잡한 모드 특성을 보이는 것을 확인하였다. 따라서 에어마스커에서 소음 감쇠성능 관점에서 기포층과 선체와의 간격을 가능한 한 작게 유지하는 것이 유리할 것으로 판단된다.
IV. 결 론
본 논문에서는 해양구조물의 파일링 소음을 줄이기 위한 기포커튼과 선체 진동에 의한 수중방사소음 차단을 위한 에어마스커에 대해 각각의 삽입손실 해석해를 구하였다. 이를 위해 기포커튼과 에어마스커를 각각 ‘유체-기포층-유체’ 그리고 ‘진공-평판-유체-기포층-유체’의 단순 모델로 가정하였고 각 모델에서 해당 기포층을 복소수 형태의 파수와 임피던스로 규정된 유효매질로 치환하였다. 기포커튼 모델에서는 평면파로 가정한 입사파와 기포층을 통과한 투과파의 음향 파워 비율을 삽입손실을 정의하였고, 에어마스커 모델에서는 평판의 가진에 의한 원거리 방사음장을 기포층의 유무에 따라 각각 구한 후, 두 음장 파워 비로써 삽입손실을 정의하였다.
수치모의 결과 기포층의 두께와 기포율이 증가할수록 삽입손실이 급격히 커짐을 확인하였다. 저주파 영역에서 기포층 내에서의 다중 반사에 의한 모드 특성과 반공진 주파수 대역 이상의 고주파 영역에서는 음파가 감쇠 없이 기포층을 투과함을 확인하였다. 끝으로 에어마스커의 경우 기포층이 선체에서 떨어져 생성되면 중간 유체층에 의한 모드현상이 발생하므로 감쇠성능 관점에서 불리할 것으로 판단되었다.
본 연구에서 제시된 해석해는 단순 모델을 기반으로 유도되었지만 기포커튼과 에어마스커의 초기 성능을 추정하는데 유용할 것으로 판단된다.