I. 서 론
II. 쉘의 산란 현상
2.1 이론 모델
III. 수조 실험
3.1 수조 실험 개요
3.2 송신 신호 분석
3.3 표적 응답 실험 결과
IV. PWVD를 이용한 표적 식별
4.1 PWVD 개요
4.2 실험 데이터의 PWVD 결과
4.3 PWVD를 이용한 표적 식별
V. 결 론
I. 서 론
수중 표적의 음향 산란 특성은 크게 재료적 특성과 구조적 특성으로 나눌 수 있다. 얇은 두께를 갖는 탄성 구의 경우 기뢰, 잠수함, 파이프, 어뢰 등 다양한 표적으로 확장 될 수 있다. 따라서 얇은 두께의 탄성 구에 대한 산란 특성 연구는 수중 표적 탐지와 식별에 중요한 기초 연구가 된다. 쉘 구 형상의 산란 신호 해석과 측정은 기존에 많은 연구가 진행된 바 있다. 먼저 Stanton의 연구[1]에서는 여러 형상과 두께의 스테인리스 강 표적에 대하여 표적강도를 계산하였다. 표적 내부에 공기 또는 물이 채워진 경우에 대하여 이론 계산 결과를 제시하였으며, 실험에서는 외반경 대비 내반경의 비율(b/a)이 0.48인 스테인리스 강 튜브에 대한 결과를 제시하였다.
Diercks와 Hickling의 연구[2]에서는 b/a가 0.8, 0.95인 경우에 대하여 공기가 채워진 구형 알루미늄 쉘의 표적 강도를 측정하였으며, 물이 채워진 경우와 공기가 채워진 경우의 산란 신호 차이를 이론적으로 관찰한 바 있다.[3]
본 연구에서는 구형 알루미늄 쉘 내부 물질의 차이에 의한 수중 음향 산란 특성에 대한 연구를 수행하였다. 특히, b/a가 0.9인 구형 알루미늄 쉘을 이용하여 얇은 두께를 갖는 표적의 산란 특성인 MFE(Mid- Frequency Enhancement)를 관찰하였는데, 표적 내부에 공기 또는 물이 채워진 경우의 표적 강도를 측정하고 Hickling의 이론 모델[3]과 비교하였다. 표적 강도는 다중경로가 존재하는 수조환경에서 계단 주파수 스윕 사인 파형(stepped frequency sweep sine waveform)을 이용하여 표적강도를 측정하였다.[4]
구형 알루미늄 쉘의 내부 물질 차이에 의한 표적 산란 신호를 관찰하기 위하여 유사 위그너-빌 분포(Pseudo Wigner-Ville distribution; 이하 PWVD)를 이용하여 시간-주파수 분석을 수행하였다. PWVD는 시간-주파수 분석 기법 중 하나로, 스펙트로그램보다 해상도가 우수하여 표적의 산란 신호와 같이 시간 축상에서 신호를 분리하여 해석하고자 할 때 적합한 것으로 알려져 있다.[5], [6]
II. 쉘의 산란 현상
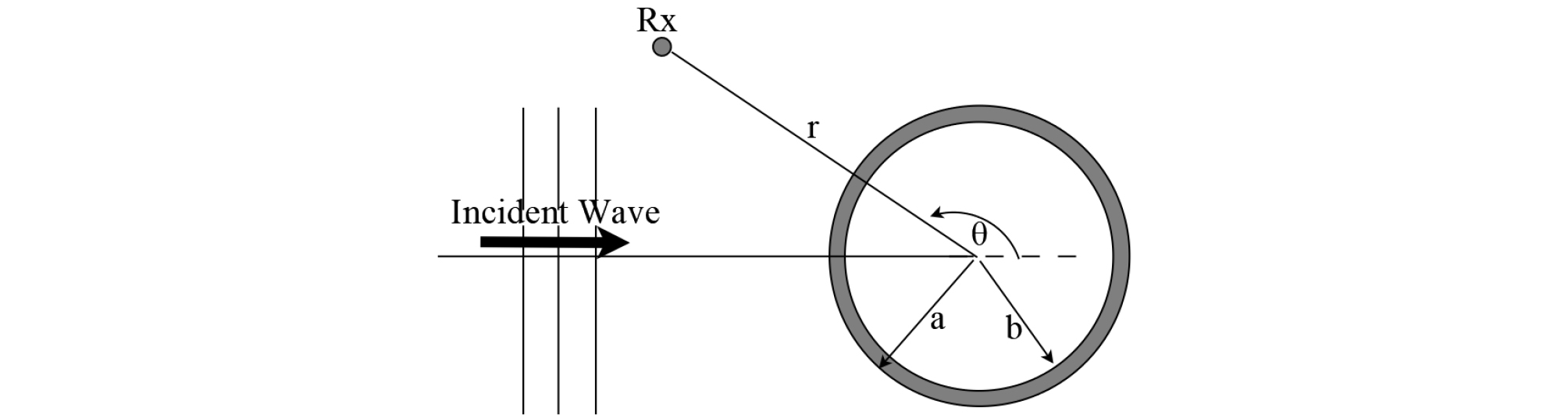
얇은 두께를 갖는 쉘 구는 음파가 입사되면 램파(Lamb wave)가 생성된다. 램파에는 탄성체 판의 단면을 중심으로 대칭이 되는 S(Symmetric)파와 A(Antisymmetric)파로 나뉜다. 특히, A파는 판의 주변 유체로 전파가 잘 일어나 누설 램파(leaky Lamb wave)가 생성된다(Fig. 1). 쉘의 단면에서 볼 때, 표적의 둘레를 따라 시계방향과 반시계방향의 누설 램파가 생성되어 음파가 입사된 방향에서 합쳐진다. 특정 주파수에서는 표면에서 반사된 경면 반사파(specular wave)보다 더 큰 누설 램파가 관측되고 이러한 현상을 MFE (Mid-Frequency Enhancement)라고 부른다.[6], [7], [8], [9]
2.1 이론 모델
구형 알루미늄 쉘의 산란 모델은 Hickling의 연구결과[3]를 이용하여 Eq. (1)과 같이 산란된 음파를 계산하였다.
| $$P_s=P_ik\sum_{n=0}^\infty{(-1)}^n(2n+1)c_nh_n(kr_o)h_n(kr)P_n(\cos\theta).$$ | (1) |
Pi는 입사되는 음파의 크기이고, k는 파수, cn은 경계조건 계수, hn은 구형 Hankel 함수, Pn은 Legendre 다항식이다. n은 모드수로 수치해석에서 결과가 수렴되는 100까지 고려하였다. 음파는 표적에 평면파로 입사됨을 가정하였다. 표적의 외부 혹은 내부의 유체는 전단응력과 점성을 갖지 않는 이상유체로 가정하며 외부 유체는 무한한 공간을 가정하였다.
Fig. 2의 a는 표적의 외반경, b는 표적의 내반경, r은 표적의 중심으로부터 산란 신호 수신위치까지의 거리를 나타낸다. θ는 표적에 입사된 신호의 방향으로부터 수신 위치까지 각도를 의미한다.
이론 모델에서 고려한 재료의 물성치는 Table 1에 정리하였다.
Table 1. Material properties.
| Density | CL | CT | |
| Water | 1000 kg/m3 | 1475.5 m/s | 0 |
| Air | 1.29 kg/m3 | 331 m/s | 0 |
| Aluminum 6061 | 2700 kg/m3 | 6148.9 m/s | 3097.3 m/s |
| H.I.P.S.[10] | 1041.2 kg/m3 | 2059.6 m/s | 804.4 m/s |
III. 수조 실험
3.1 수조 실험 개요
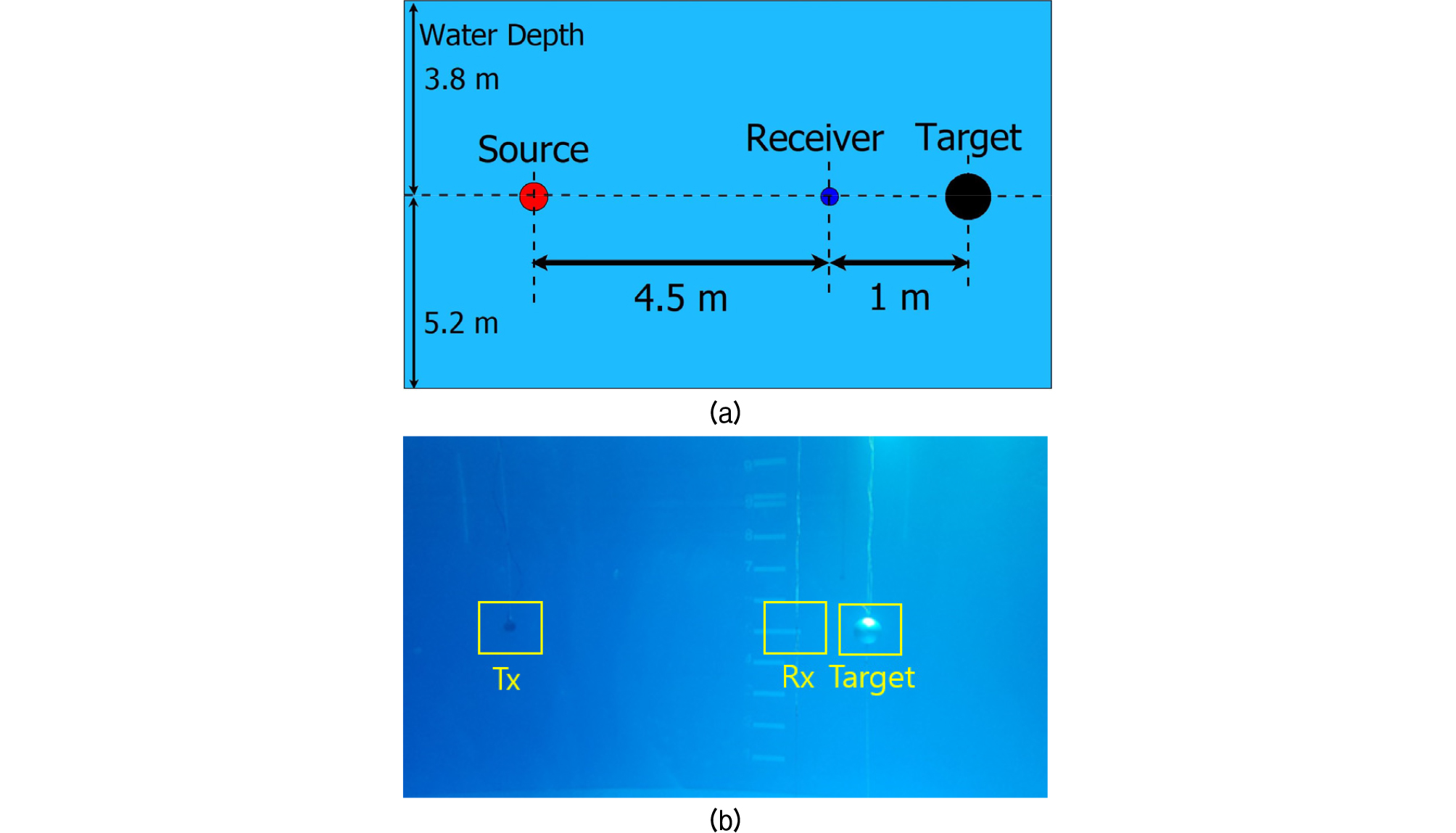
수조 실험은 포항에 위치한 수중로봇복합실증센터(Underwater robotics Test & Evaluation Center,UTEC)에서 실시되었으며, 수조의 제원은 L35 m × W20 m × D9 m이다. Fig. 3와 같이 송신 센서는 표적으로부터 5.5 m, 수신 센서는 1 m 간격을 두어 설치되었다. 송신 센서, 수신 센서 그리고 표적을 일직선상에 두어 표적에 입력되는 신호와 표적에서 반사되는 신호를 측정하였다. 송신 주파수는 500 Hz ~ 24 kHz으로 송신 센서, 수신 센서 그리고 표적 모두 수심 3.8 m에 설치되어 측정되었다. 실험에 사용된 표적은 속이 비어있는 구형 플라스틱 쉘과 구형 알루미늄 쉘이며, 제원은 Table 2와 같다. 구형 알루미늄 쉘의 위, 아래에 마개가 부착되어있어 공기를 채운 경우는 마개를 닫고, 물을 채울 경우 마개를 열어 수조에 설치하였다.
Table 2. Target size (*The thickness of the plastic spherical shell is an estimated value from its weight and buoyancy).
| Material | Outer diameter | Thickness |
| H.I.P.S. | 47 cm | 9 mm* |
| Aluminum 6061 | 41 cm | 20 mm |
3.2 송신 신호 분석
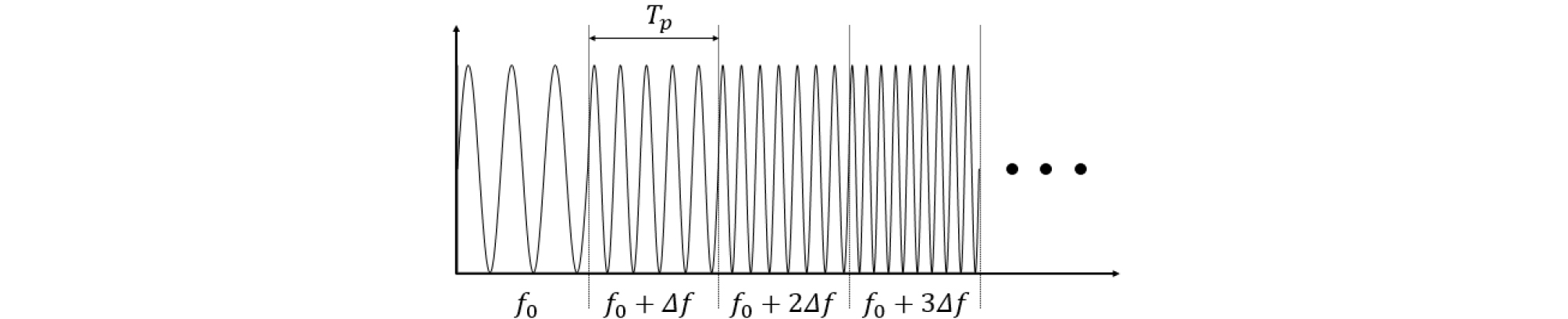
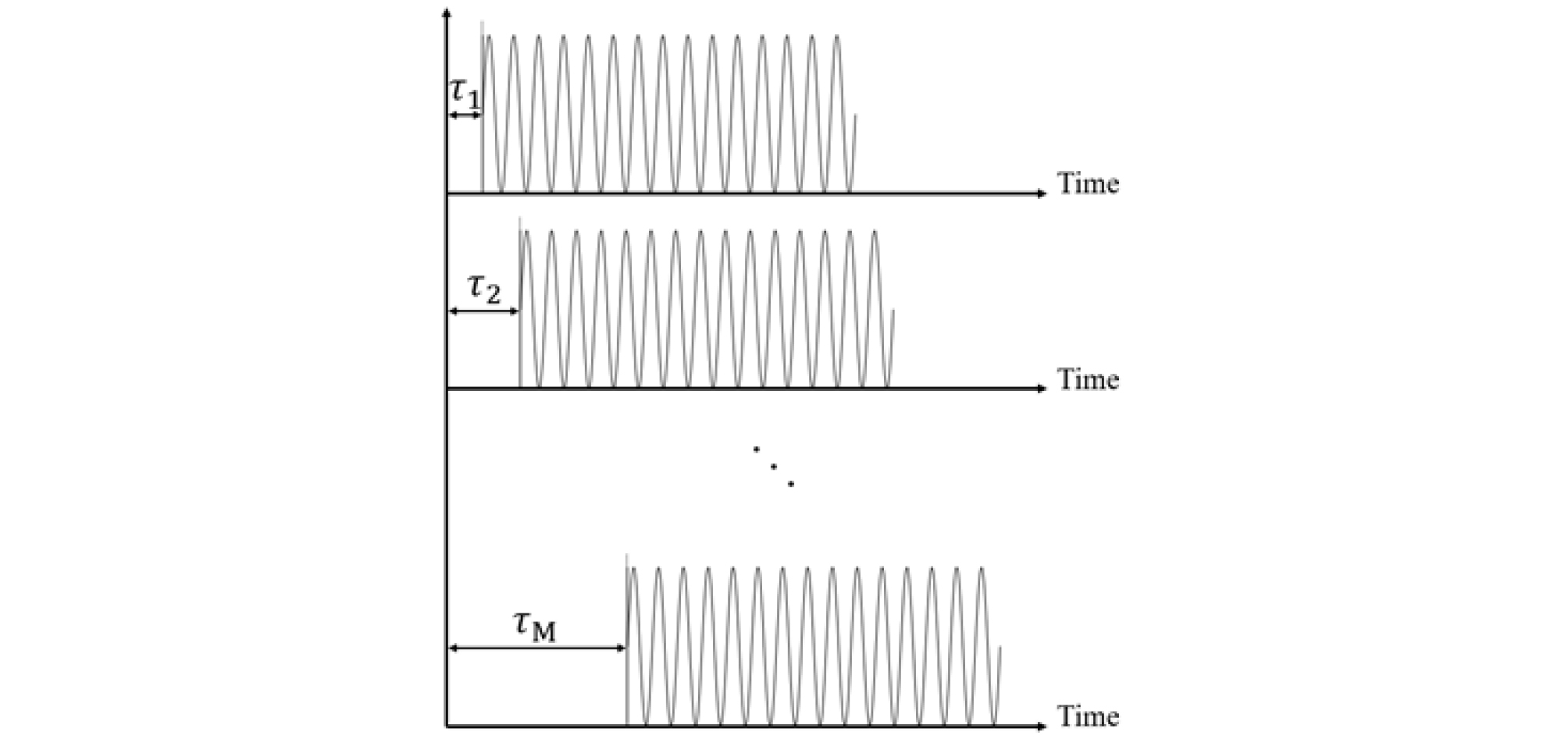
본 연구에서 사용한 계단 주파수 스윕 사인은 Fig. 4와 같이 시간 Tp 동안 f0의 톤신호가 송신되고 Δf만큼 주파수가 증가하여 Tp 동안 주파수f0 + Δf 신호가 송신된다. Fig. 5처럼 송신된 신호가 다중경로에 의해 수신될 때, 시간 지연은 τ1에서τM까지 고려할 수 있다. τM 이후의 다중경로는 감쇠에 의해 고려하지 않을 때, τM 이후에 수신된 신호는 정상상태의 신호가 된다. 본 연구에서는 수조 특성을 반영하여 τM을 0.25 s로 정하였고, 수신된 신호는 푸리에 변환을 통해 표적의 임펄스응답을 구할 수 있다.[4]
3.3 표적 응답 실험 결과
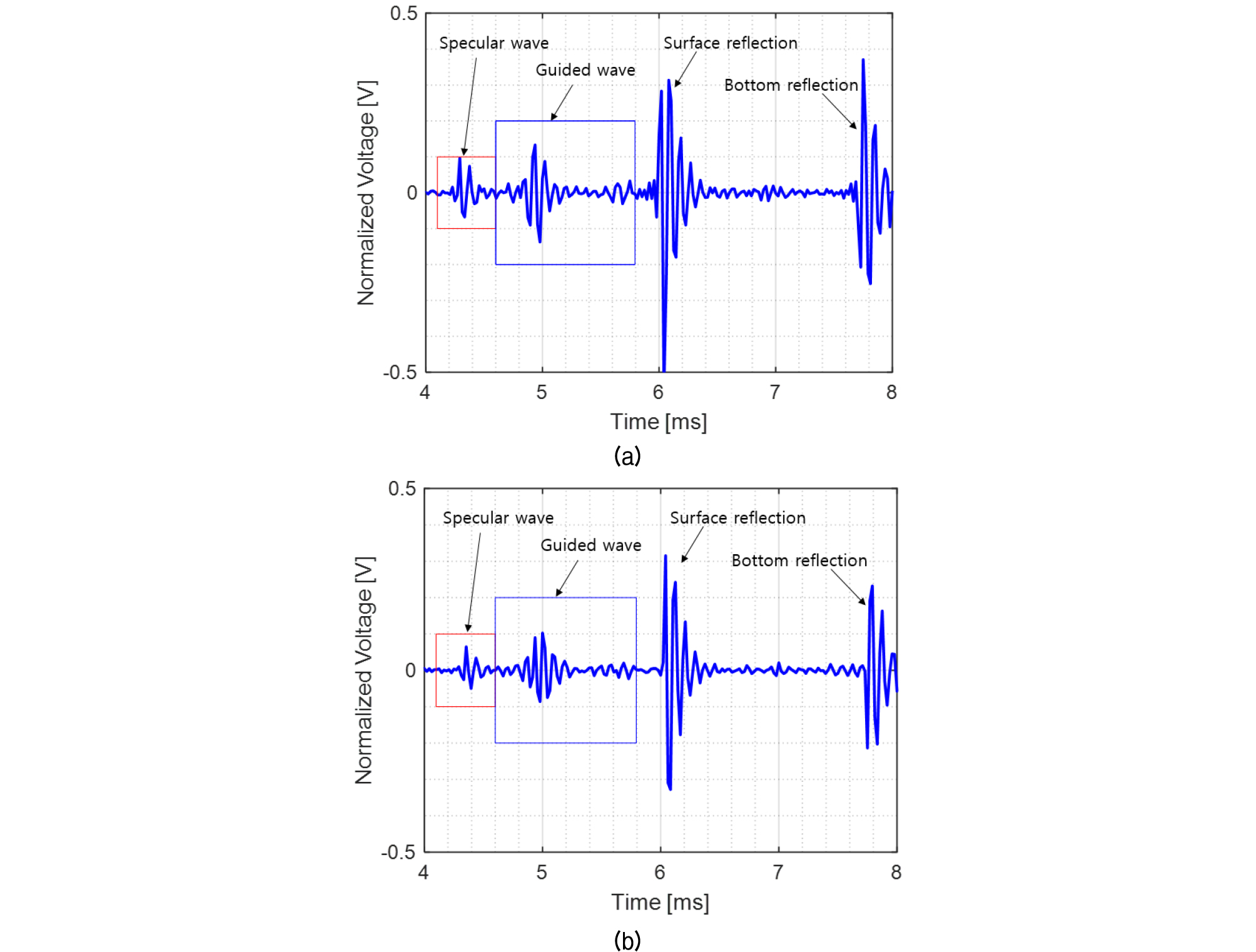
500 Hz ~ 24 kHz의 구형 알루미늄 쉘과 플라스틱 쉘 구에 의한 음파 산란 신호는 Figs. 6, 7과 같이 관찰되었다. 송신 센서의 주파수 송신 특성으로 정규화하지 않았으나 표적 상태에 따른 상대적인 비교가 가능하다. 구형 알루미늄 쉘 표적의 경우, 공기가 채워진 경우와 물이 채워진 경우 모두 경면 반사파 이후 유도파가 관찰 되었다. Fig. 6(a)는 공기가 채워진 구형 알루미늄 쉘의 산란 신호, (b)는 물이 채워진 구형 알루미늄 쉘의 산란 신호이다. 약 4.3 ms에서 경면 반사파가 도달하고, 약 4.8 ms부터 유도파가 관찰되었다. 표적의 설치 위치 차이로 인하여 (b)에서 경면 반사파와 유도파가 (a)보다 약간 늦게 하이드로폰에 도달한 것으로 판단된다.
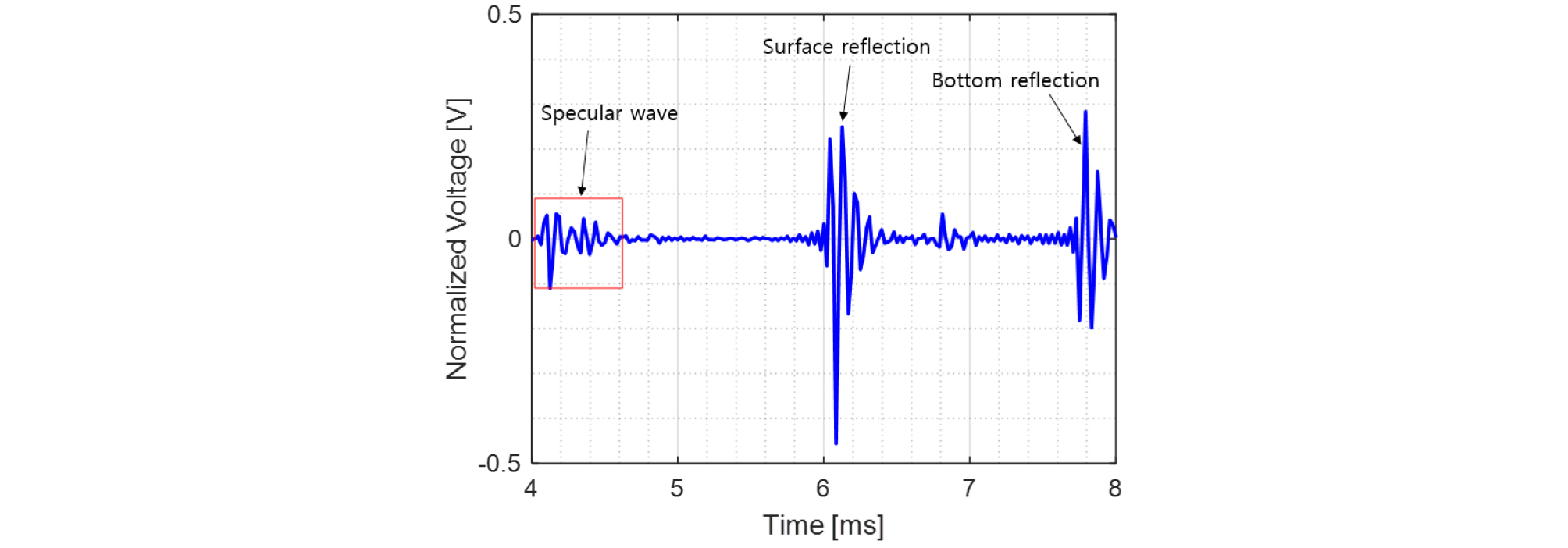
구형 플라스틱 쉘 표적의 경우(Fig. 7) 경면 반사파 이후 수면 반사파가 입사될 때까지 다른 신호는 관찰되지 않았으며, 6.8 ms 근처에서 약한 성분이 검출되었다. 이는 플라스틱 쉘 구에서 형성되는 램파의 속도가 구형 알루미늄 쉘보다 매우 느리기 때문인 것으로 추정된다. Fig. 7에서 플라스틱 쉘 구의 경면파가 Fig. 6의 구형 알루미늄 쉘의 경면파보다 빠르게 도달한 것은 표적 설치 과정에서 플라스틱 쉘 구의 위치가 구형 알루미늄 쉘의 경우보다 가깝게 설치되었기 때문이다.
표적강도는 표적에 입력된 신호와 산란된 신호를 나누어 Eq. (2)와 같이 계산하였다. Pi은 표적에 입사된 음파의 크기이고, Pr은 표적으로부터 산란된 음파의 크기로 주파수에 대한 함수이다.
| $$TS=20\log10\frac{P_r}{P_i}.$$ | (2) |
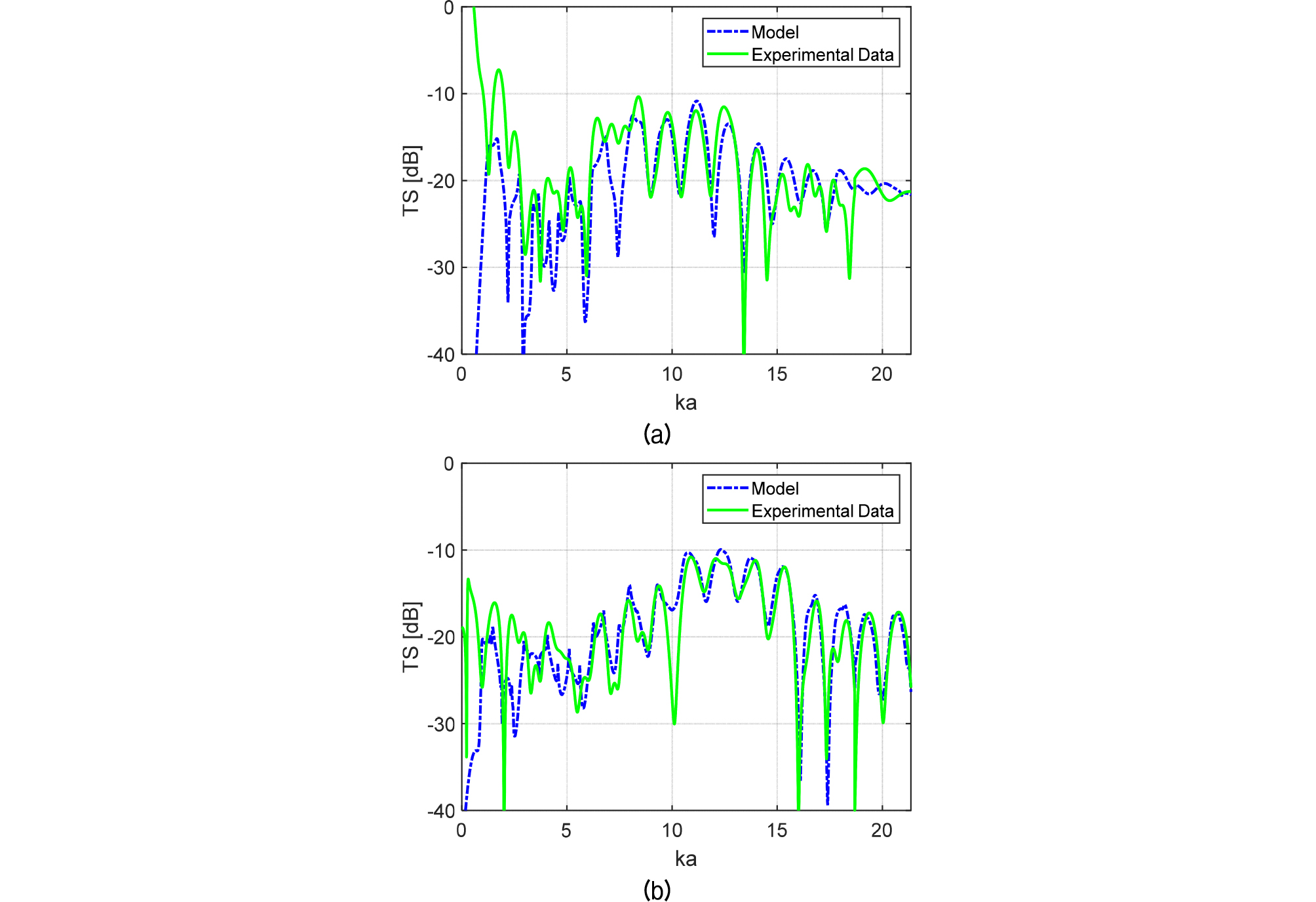
구형 알루미늄 쉘의 표적 강도는 Fig. 8와 같이 모델링 결과와 비교하였다. ka는 파수와 표적의 외반경 a의 곱으로 나타낸 무차원 변수이다.
비교 결과 실험 데이터의 피크(peak)와 널(null)의 위치가 모델링 결과와 매우 유사하게 나타났다. 공기가 채워진 경우, ka가 약 8 ~ 13에서 MFE가 나타난다. 물이 채워진 경우, ka 약 11 ~ 15에서 MFE가 나타나 공기가 채워진 경우보다 높은 주파수에서 MFE가 관찰 된다.
IV. PWVD를 이용한 표적 식별
4.1 PWVD 개요
PWVD는 대표적인 시간-주파수 분석 방법으로 WVD(Winger-Ville distribution)의 단점인 간섭항(cross term)을 줄이기 위해 창 함수가 포함된 형태로 신호 x(t)에 대해 Eq. (3)와 같이 표현된다.
w는 창 함수로 0.25 ms 길이의 해밍 함수를 사용하였다.
4.2 실험 데이터의 PWVD 결과
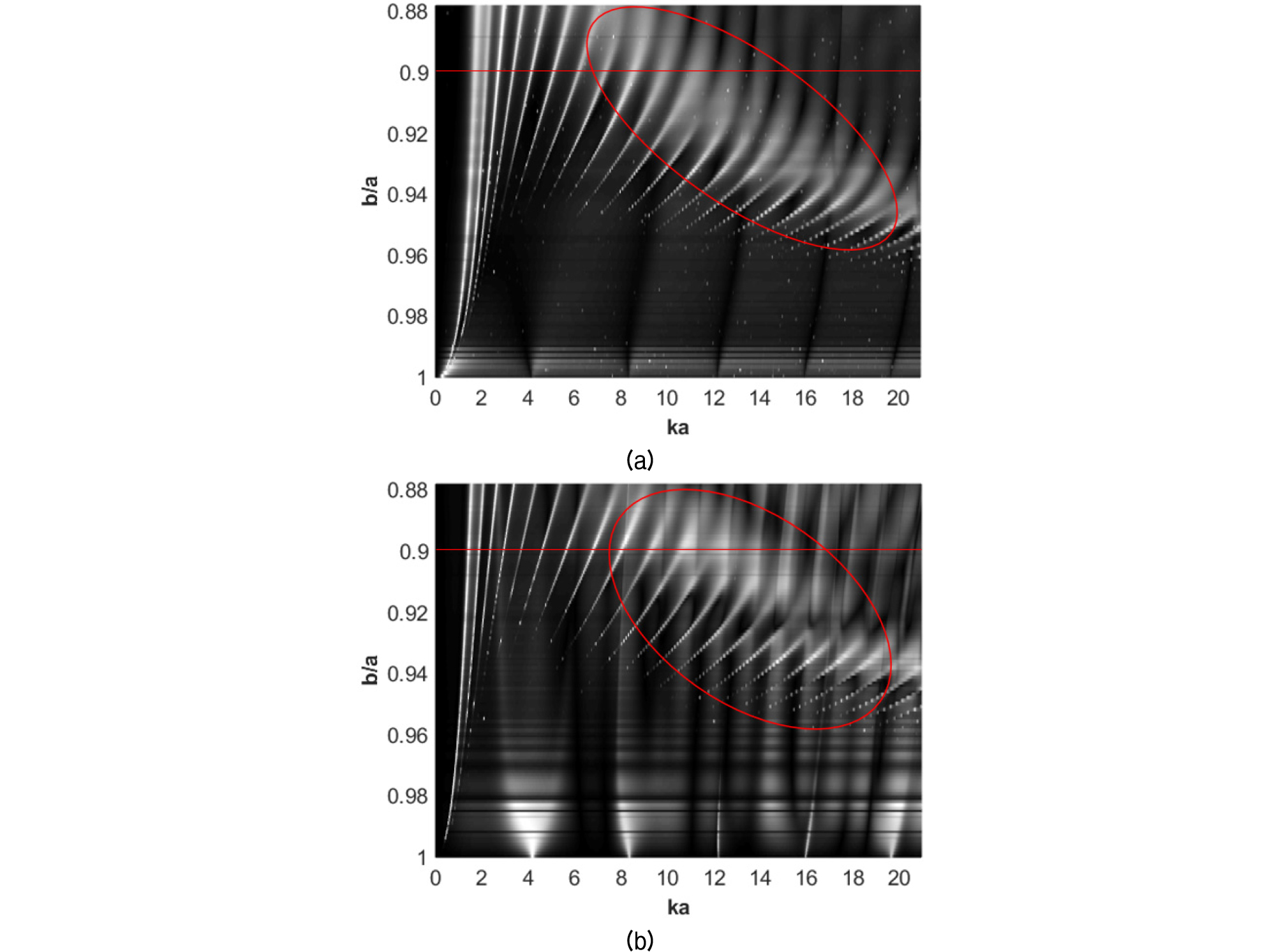
Eq. (1)을 이용하여 계산된 알루미늄 표적의 두께와 주파수에 따른 산란 전달 함수는 Fig. 9과 같다.[11]b/a는 외반경 대비 내 반경으로 1에 가까울수록 얇은 두께를 의미한다. 알루미늄 구 실험 표적의 b/a는 0.9이며, Fig. 8의 결과는 Fig. 9의 붉은색 선분에 해당된다.
얇은 두께의 구형 알루미늄 쉘은 특정 주파수에서 MFE가 발생하고 Fig. 9의 표시된 원에 해당된다. 두께가 얇아질수록 MFE의 중심주파수가 증가한다.[10] 구형 알루미늄 쉘에 물이 채워진 경우, 공기가 채워진 경우보다 같은 두께에서 MFE의 주파수가 높게 나타난다. 구형 알루미늄 쉘 외부의 물과 알루미늄의 임피던스 차이가 적어 표적의 외부에서 누설 램파가 발생한다. 표적의 내부에 공기가 채워진 경우 알루미늄과의 임피던스 차이가 커서 누설 램파가 작다. 물이 채워진 경우, 음향 임피던스 차이가 상대적으로 작으므로 누설 램파가 구형 알루미늄 쉘 내부에서도 강하게 생성된다. 표적 내부에서 생성된 누설 램파는 내벽에 부딪혀 표적 외부로 전달되는 누설 램파를 생성한다.[2], [3], [12] 따라서 표적 내부에 물이 채워진 경우 내부파에 의해 발생하는 누설 램파가 더해져 공기가 채워진 경우보다 큰 유도파가 관찰된다.
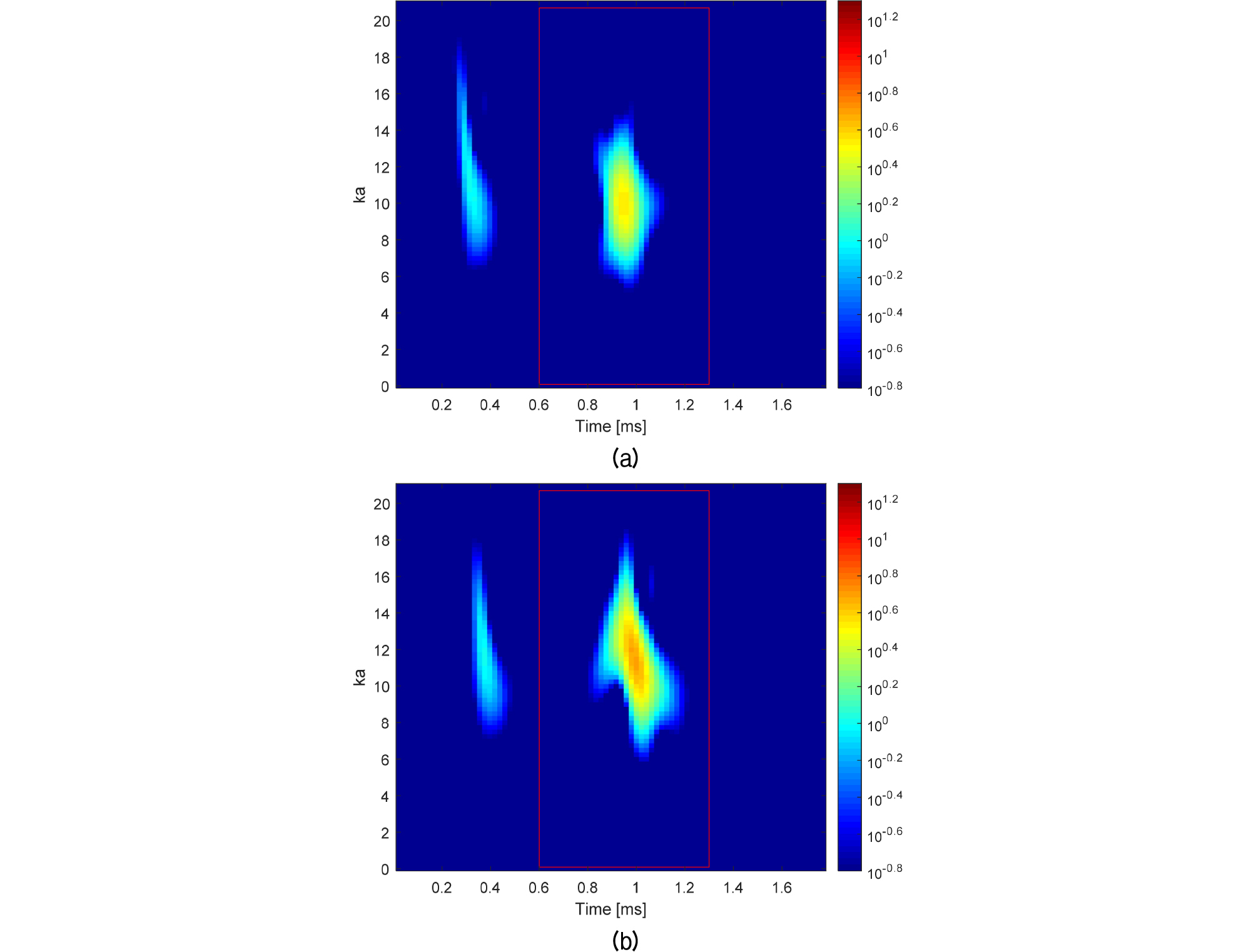
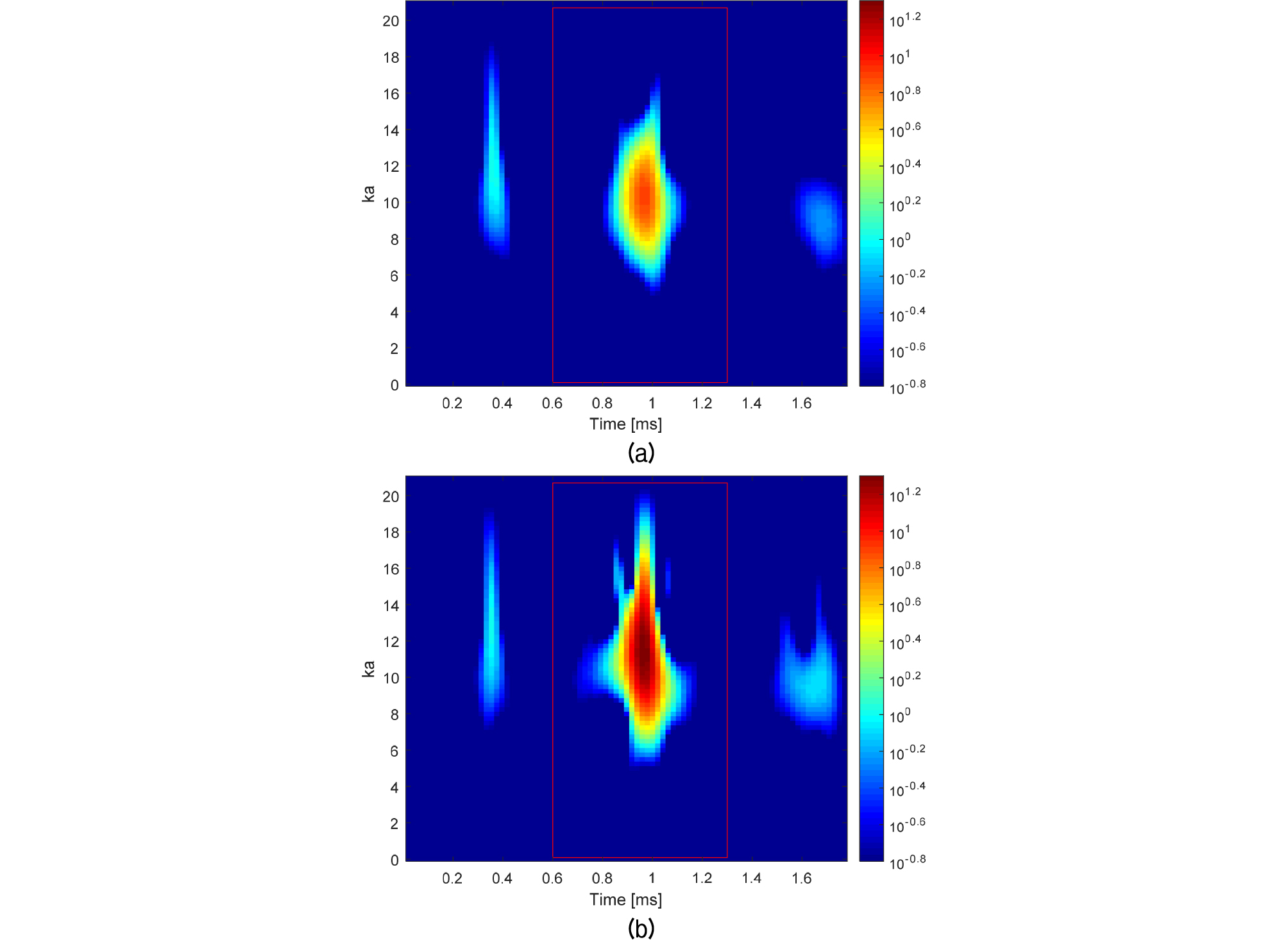
Fig. 10은 Fig. 6에 나타낸 실험 결과의 산란파를 이용하여 PWVD로 분석한 결과를 나타낸 것이다. 약 0.38 ms에 도달한 신호는 표적의 표면에서 산란된 경면 반사파이고 1 ms근처의 붉은색 상자 안의 신호가 유도파이다. Fig. 11은 이론 모델 결과를 이용하여 표적의 산란파를 PWVD로 나타낸 것이다. PWVD는 경면 반사파를 기준으로 정규화 하였다. Figs. 8과 9의 산란 강도에 나타난 바와 같이 표적 내부에 공기가 채워진 경우보다 물이 채워진 경우 유도파의 중심 주파수가 증가하였다. Fig. 10의 실험 데이터와 Fig. 11의 모델 모두 물이 채워진 경우에 유도파가 더 크게 나타난다. 이와 함께 이론 모델에서 경면 반사파와 유도파의 차이가 더 큰 것으로 나타나 실험 결과보다 큰 차이를 보였다. 이러한 오차는 표적 제작 과정 중 발생하는 설계와의 차이에 기인한 것으로 추정된다.[13] 실험 결과에서 나타난 표적 내부 유체에 의한 유도파 차이가 실제 환경에서도 식별이 가능한지 추가적인 연구가 필요할 것으로 판단된다.
4.3 PWVD를 이용한 표적 식별
본 절에서는 수조실험을 통해 계측된 유도파의 평균 주파수(favg), 주파수 분포(σf), 에너지(E)를 이용하여 알루미늄 구의 내부 유체에 따른 차이를 분석하였다. Figs. 9와 10의 붉은색 상자로 표시된 영역과 같이 유도파의 0.6 ms ~ 1.3 ms의 PWVD를 이용하였다.
평균 주파수는 유도파의 1차 모멘트를 이용하여 Eq. (4)와 같이 계산되었다.
| $$f_{avg}=\frac{\int PWVD(t,\;f)dt\ast f}{\iint PWVD(t,f)dtdf}.$$ | (4) |
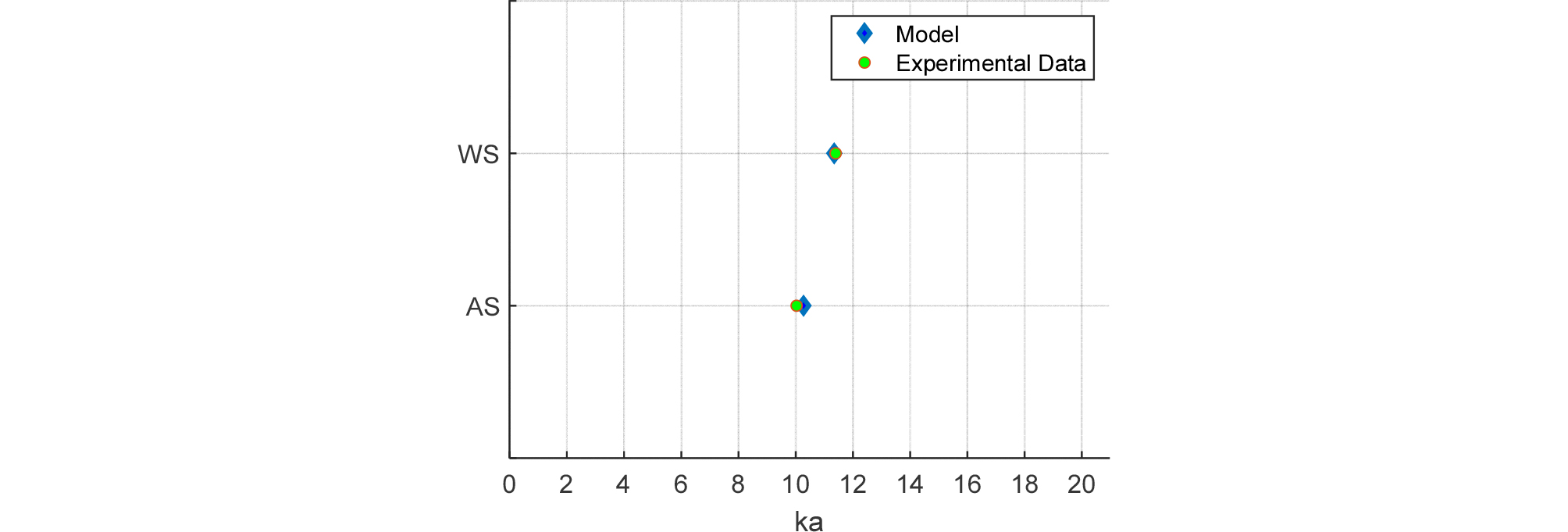
Fig. 12는 모델과 실험 데이터의 평균 주파수를 나타낸 것으로, 앞 절에서 예상된 바와 같이 물이 채워진 경우가 공기가 채워진 경우보다 높은 평균 주파수를 갖는다.
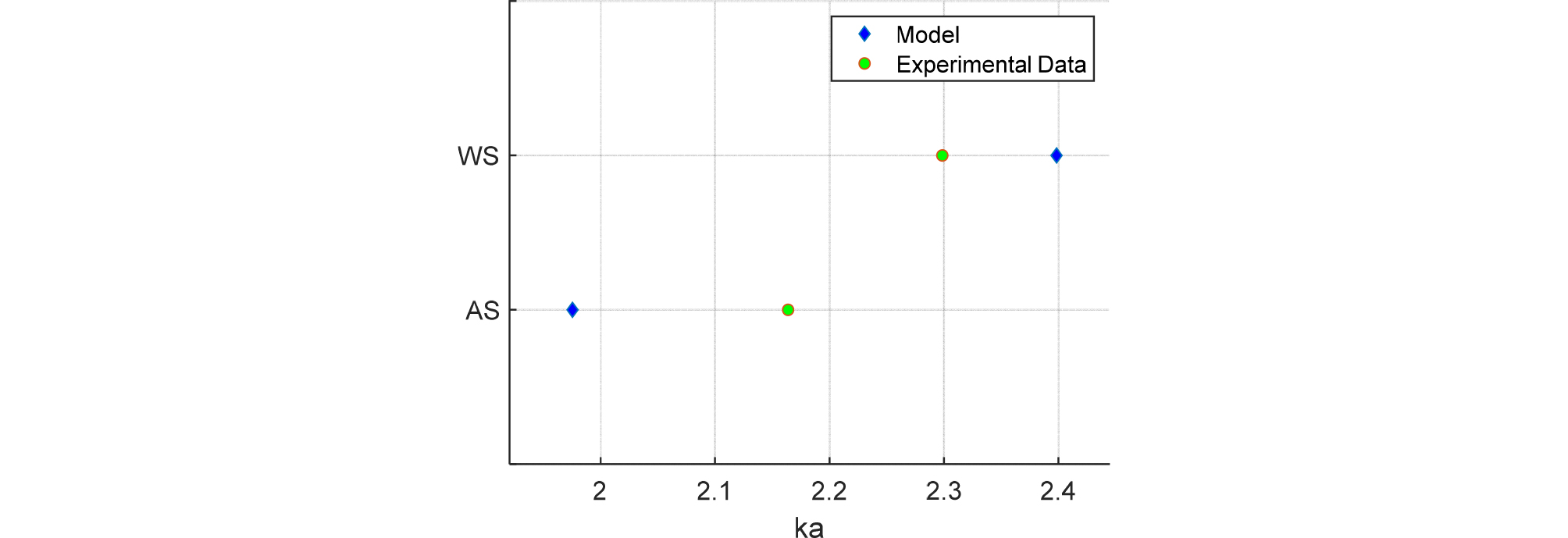
유도파의 주파수 분포는 Eq. (5)와 같이 주파수 상의 표준편차로 계산되어 Fig. 13에 나타냈다.
| $$\sigma_f=\sqrt{\frac{\iint PWVD(t,\;f)dt\ast{(f-f_{avg})}^2df}{\iint PWVD(t,f)dtdf}}.$$ | (5) |
이론 모델과 실험 결과 모두 구형 알루미늄 쉘에 물이 채워진 경우가 공기가 채워진 경우보다 주파수 상에서 더 넓은 분포를 갖는 것으로 관찰되었다. 물이 채워진 경우, 공기가 채워진 경우와 달리 표적 내부에서 생성된 누설 램파가 내벽에 반사되면 또 다른 경로의 누설 램파를 생성하기 때문이다.[12] Fig. 10의 실험 결과에서는 Fig. 11의 이론 모델에 비해 평균 주파수(favg)에 해당되는 주파수 성분이 작게 계측 되었다. 따라서 표적에 공기가 채워진 경우 주파수 표준 편차(σf) 값이 더 크게 나타났다. 표적에 물이 채워진 경우, 평균 주파수(favg) 이외의 주파수 성분이 Fig. 10의 실험에서 작게 계측 되어 주파수 표준 편차 값이 더 작게 나타났다.
이론 모델에서 실험 결과보다 유도파가 작게 계측된 것은 표적으로 사용된 구형 알루미늄 쉘의 설계와 제작 사이의 차이로 추정된다. 구형 알루미늄 쉘의 제작 시 주조(casting)가 아닌 육면체 알루미늄의 내부와 외부를 원형으로 깎아내고 두 개의 반구를 용접하여 만들었다. 따라서 표적의 설계와 제작 결과가 다소 차이가 있을 수 있다.
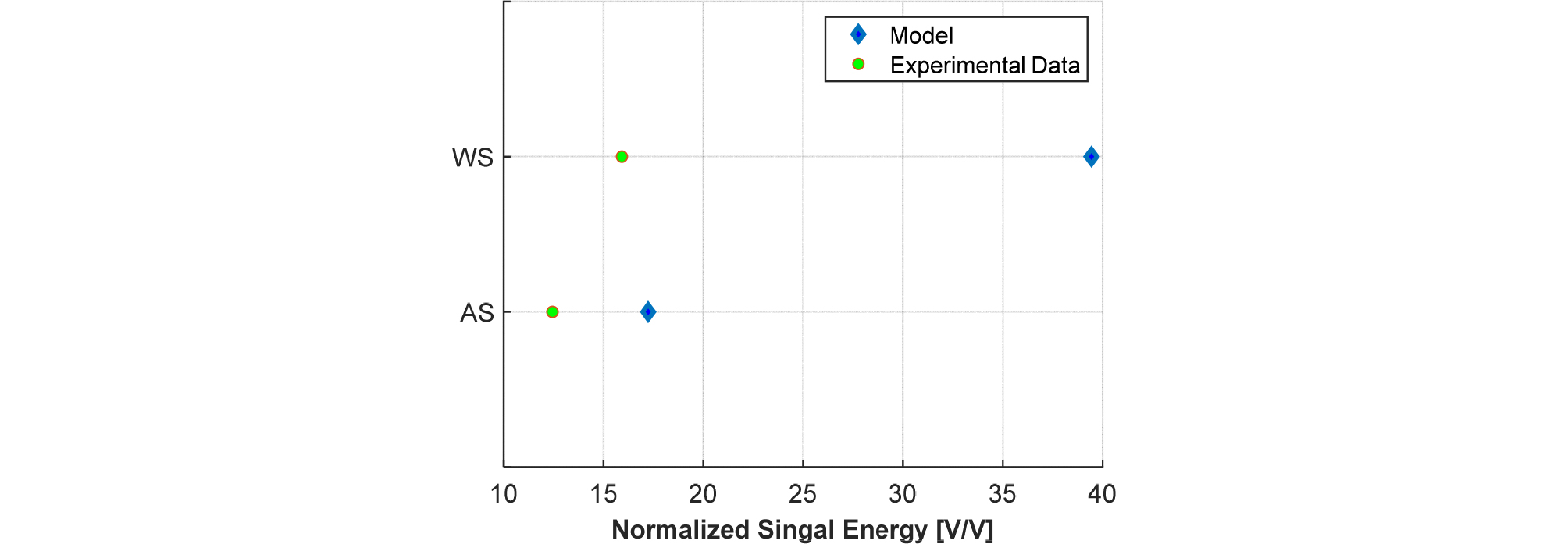
유도파의 에너지는 Fig. 6의 유도파(guided wave)로 Eq. (6)의 식을 이용하여 계산하였다. Fig. 14는 계산 결과를 나타낸 것이다.
| $$E=\int\left|S_N(t)\right|^2dt.$$ | (6) |
SN(t)은 경면 반사파의 최대 진폭으로 정규화된 유도파이다. 이론 모델과 실험 결과 모두 물이 채워진 구형 알루미늄 쉘에서 유도파의 에너지가 높게 나타났다.
Fig. 14의 유도파의 에너지에서 물이 채워진 경우가 공기를 채운 경우보다 이론 모델과 실험 결과의 차이가 더 크게 나타났다. 이는 앞서 언급한 구형 쉘 제작 과정의 오차와 수조 실험에서 물을 채운 표적을 설치할 때의 위치 오차 등에 의해 복합적으로 나타난 것으로 추정된다.
V. 결 론
본 연구에서는 속이 빈 얇은 두께의 구형 알루미늄 쉘에 대한 음향 산란의 이론 모델과 수조 실험 결과를 비교하였다. 구형 알루미늄 쉘과 플라스틱 쉘 구의 실험 결과를 통해 재질에 따른 유도파의 차이를 확인하였다. 또한, 산란 신호의 유도파를 이용하여 알루미늄 구 내부에 공기가 채워진 경우 보다 물이 채워진 경우에 평균 주파수(favg), 주파수 분포(σf), 에너지(E)가 증가함을 확인 하였다.
이론 모델에서도 물이 채워진 경우가 공기가 채워진 경우보다 평균 주파수, 에너지, 주파수 분포가 증가하였다. 이는 물이 채워진 표적 내부에서 생성되는 누설 램파에 의한 효과다. 하지만 실험 결과가 이론 모델보다는 주파수 분포 차이와 에너지 차이가 작게 나타나며 표적의 설계와 제작 사이의 오차로 추정된다.
해당 결과는 표적의 내부 물질을 음향으로 분류하는 연구에 활용될 수 있다.