I. 서 론
II. 주파수-시간 공간 변환
2.1 지진파 데이터
2.2 SPECTROGRAM
2.3 MEL-SPECTROGRAM
III. 지진파 분류를 위한 특징 추출방법
3.1 히스토그램 기반 주파수 특징 추출
3.2 히스토그램 기반 주파수-시간 특징 추출
3.3 PCA 기반 주파수 특징 추출
3.4 PCA 기반 주파수-시간 특징 추출
3.5 고주파 대역 필터를 통한 전처리
IV. 모의실험
4.1 전처리 유무에 따른 Spectrogram vs Mel- spectrogram 특징 성능 비교
4.2 주파수 특징 vs 주파수-시간 특징 성능 비교
4.3 히스토그램 기반 특징 vs PCA 기반 특징 성능 비교
V. 결 론
I. 서 론
기상청 제공 지진 연보 자료에 따르면 2000년도 이후 지진 발생 규모 및 횟수가 증가하고 있다.[1] 최근 경주와 포항에서 발생한 규모 5.0 이상의 강진으로 인해 국내에서도 지진 경보 시스템이 크게 주목받고 있다. 지진 경보 시스템은 주로 강진을 대상으로 한 경보에 초점을 맞추고 있지만, 국내에서 발생 되는 지진의 경우 미소지진 및 인공지진도 관심 대상이 되고 있다. 지진 경보 시스템에서 지진 분류는 핵심 사안으로서 강진 외에 미소지진, 인공지진을 분류하는 것이 다양한 지질학적인 잡음 요소로 인해 난제가 되고 있다.
지진 자동 분류문제는 대표적인 시계열 데이터 분류(time series classification)문제로서 입력되는 미가공 지진 신호 혹은 변환 공간에서 의미 있는 정보를 추출한 후 문턱치 혹은 학습기반 결정 규칙을 통해 지진을 분류하게 된다. 특징 추출은 지진 분류 결정 규칙을 만들기 위해 입력 미가공 지진 신호를 적합한 공간으로 변환하여 의미 있는 정보를 생산하는 과정을 말한다. 변환 공간에서의 데이터 표현 구분성이 향상될수록 결정 규칙 혹은 분류 성능의 향상을 기대할 수 있다.
특징 추출은 크게 시간, 주파수, 주파수-시간 측면으로 구분할 수 있다. 시간 측면은 미가공 지진 신호 공간에서 파형 특성 관련 특징 획득에 유용하다. Langet et al.[2]은 지진 신호에 슬라이딩 윈도우 방식을 적용하여 첨도 파형을 생성하여 초동정보가 강화된 파형과 연속적인 지진 천이로 진앙과 지진을 자동 검출한다. Bai와 Kennett[3]은 3채널 지진 신호로부터 에너지, 주파수, 파형 상관관계 특징을 추출하여 지진의 위상 검출과 식별을 자동으로 하는 방법이 제안되었다. Caffagni et al.[4]는 연속 신호 지진 데이터와 템플릿 지진 이벤트의 상호 관계를 기반으로 지진 이벤트 후보를 생성한다. 지진 이벤트 후보에서 템플릿 지진 이벤트의 진원과 지진 규모와의 상호 상관관계로 미소지진을 검출하는 방법이 제안되었다. 또한, 최적화 필터가 적용된 음성 검출알고리즘을 이용하여 화산 지진 이벤트의 끝점 추정이 가능한 검출기를 제안하였다.[5]
주파수 특징은 지진 신호의 푸리에변환(Fourier transform)을 통해 데이터의 스펙트랄 특징을 파악하는 방법이다. 주파수 특성만을 이용하는 방식보다는 Short Time Fourier Transform(STFT)을 통해 시간에 따른 주파수 특성을 이용한 연구들이 주목을 받고 있다. Suriñach et al.[6]은 지진파 신호에서 스펙트로그램 을 생성 후 시간에 따른 주파수와 신호 크기의 변화를 특징으로 이용하여 지진을 검출하는 방법이 제안되었으며 Wang과Teng[7]은 스펙트로그램 값을 인공신경망의 훈련 데이터로 사용하여 지진을 검출하는 방법이 제안되었다. Köhler et al.[8], [9]는 고차원 데이터셋에서 안정적인 성능이 보장되는 자기 조직화 지도를 이용하여 특징 선별, 시각화, 분류 작업을 수행하며 단시간 윈도우 상에서 주파수-파수, 분극, 스펙트럴 분석을 포함한 특징 벡터를 추출하여 지진 신호를 분류하였다. 주파수-시간 특징 공간에서 통계적인 특징을 추출하는 연구들도 보고 되고 있다. Tian et al.[10]은 spectral statistics and Wavelet coefficients characterization을 토대로 스펙트럼, 에너지 스펙트럼 밀도, 웨이블릿 계수를 특징으로 이용하여 지진 신호를 분류하였다. Synchro Squeezing Transform(SST)을 이용하여 지진파를 분석하는 방법은 지진파처럼 순간 주파수 변화가 생기는 신호에 대하여 기존 STFT나 웨이블릿 분석이 대응하지 못하는 한계를 극복하고자 Continuous Wavelet Transform(CWT)을 적용하여 초기 주파수 값을 추정한 후 SST를 적용하여 지진을 탐지하였다.[11]
본 연구에서는 지진(자연지진, 인공지진) 분류를 위해 주파수-시간 공간상에서 특징 추출방법을 제안한다. 자연지진의 경우 강진과 미소지진으로 분류할 수 있으며 잡음은 지진 외에 관측되는 다양한 지질학적인 잡음 및 배경 잡음을 포함한다. 원시 지진 신호는 시간에 따른 주파수 특성을 파악하기 위해 STFT를 통해 주파수-시간 공간의 스펙트로그램 변환과 저주파 부분의 차이는 보존하고 고주파 부분은 압축하는 멜 스펙트로그램 변환을 이용한다. 주파수-시간 공간상에서 효과적인 특징 추출을 위해 본 논문에서는 히스토그램 기반 특징 추출방식과 주성분 기반 Principal Component Analysis(PCA) 특징 추출방식을 제안한다. 2차원의 스펙트로그램 과 멜 스펙트로그램에서 주파수축 및 시간 축 상에서 특징 정보들을 히스토그램 기반 혹은 주성분 기반으로 각각 추출한 후 주파수축 특징과 시간 축 특징을 연결하여 특징 벡터를 구성하게 된다. 제안된 특징 방식은 Support Vector Machine(SVM) 기법을 통한 분류 성능 결과를 토대로 기존의 주파수 특징 정보만 이용한 방식과의 비교 분석을 수행하였다.
본 논문의 구성은 다음과 같다. 2장에서는 본 논문에서 다루는 지진 신호와 주파수-시간 공간 변환을 설명한다. 3장에서는 본 논문에서 제안하는 주파수-시간 공간에서의 특징 추출방식을 제시한다. 4장에서는 국내지진 데이터를 이용한 제안된 특징 추출의 성능 평가를 다루며, 5장에서 결론을 맺는다.
II. 주파수-시간 공간 변환
지진파 신호의 시간에 따른 주파수 특징을 보기 위해 원시 지진 신호는 스펙트로그램과 저주파 대역을 강조한 멜 스펙트로그램으로 변환된다. 본 논문에서 다루는 지진 신호 데이터는 아래와 같은 특성이 있다.
2.1 지진파 데이터
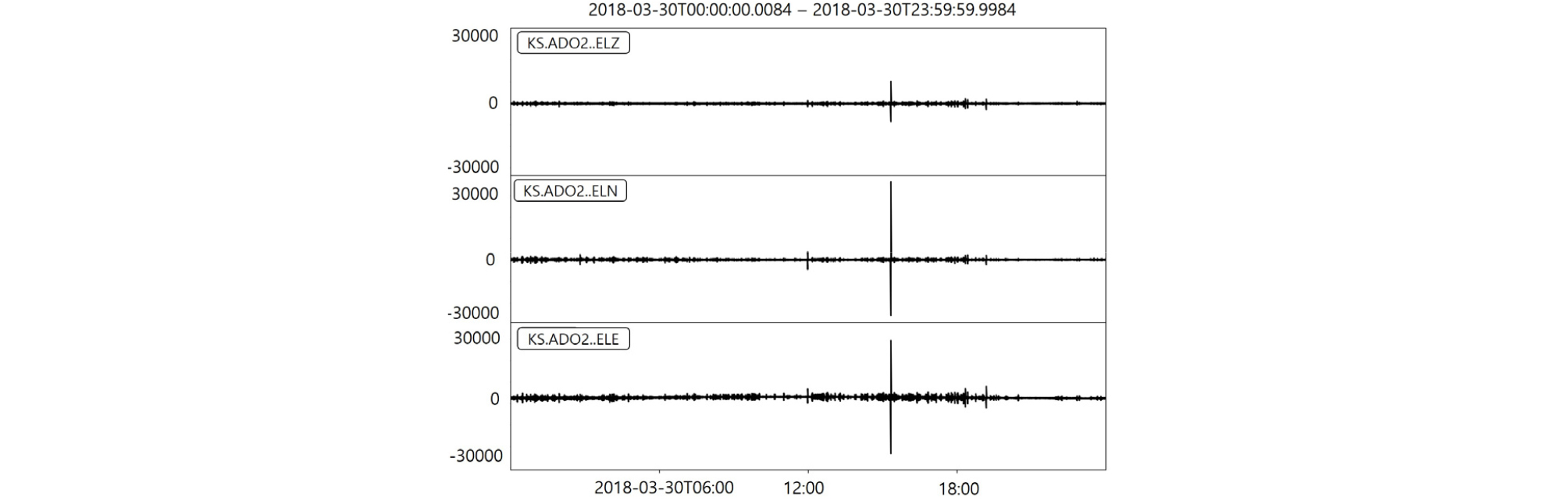
지진이 발생 되는 순간 지진 관측소에서는 속도 혹은 가속도 기록 장치를 이용하여 Fig. 1과 같이 E, N, Z의 3개 채널에 대한 관측 데이터를 생성한다. E 채널은 동쪽-서쪽, N 채널은 북쪽-남쪽, Z 채널은 지표면이 위-아래로 흔들리는 정도를 나타내는 데이터이다. 지진파 데이터는 자연 발생 여부에 따라 자연지진과 인공지진으로 구분되며 자연지진은 규모 2.0을 기준으로 강진(≥ 2.0)과 미소지진(< 2.0)으로 나뉜다. 또한, 본 논문에서는 센서 잡음 및 지질학적 배경 잡음에 관련된 부분은 잡음 카테고리로 구성하였다.
2.2 SPECTROGRAM
지진파 신호의 시간에 따르는 주파수 특성을 파악하기 위해서는 STFT를 통해 원시 지진파 신호를 스펙트로그램 공간으로 변환해야 한다. 스펙트로그램은 시간-진폭으로 표현되는 지진파 신호를 시간-주파수 형태로 변환하여 원시 지진파 신호 내의 시간에 따른 주파수 정보를 분석할 수 있게 해준다.
지진파 신호 표본에 대하여 Eqs. (1) ~ (3)과 같은 STFT를 적용하기 위해 윈도우 크기(), 윈도우 중첩 크기(), FFT bin 수() 파라메터를 설정해야 하며 파라메터에 따라 스펙트로그램의 시간 혹은 주파수 해상도가 조절된다.
| $$X(t,k)=\sum_{n=0}^{L-1}x\lbrack n\rbrack\omega\lbrack n-\tau\rbrack e^\frac{-2\pi jk(n-\tau)}L,$$ | (1) |
| $$\tau =t(L/q),$$ | (2) |
| $$Power Spectrum= \frac { | X(t,k) | ^{2}} {N},$$ | (3) |
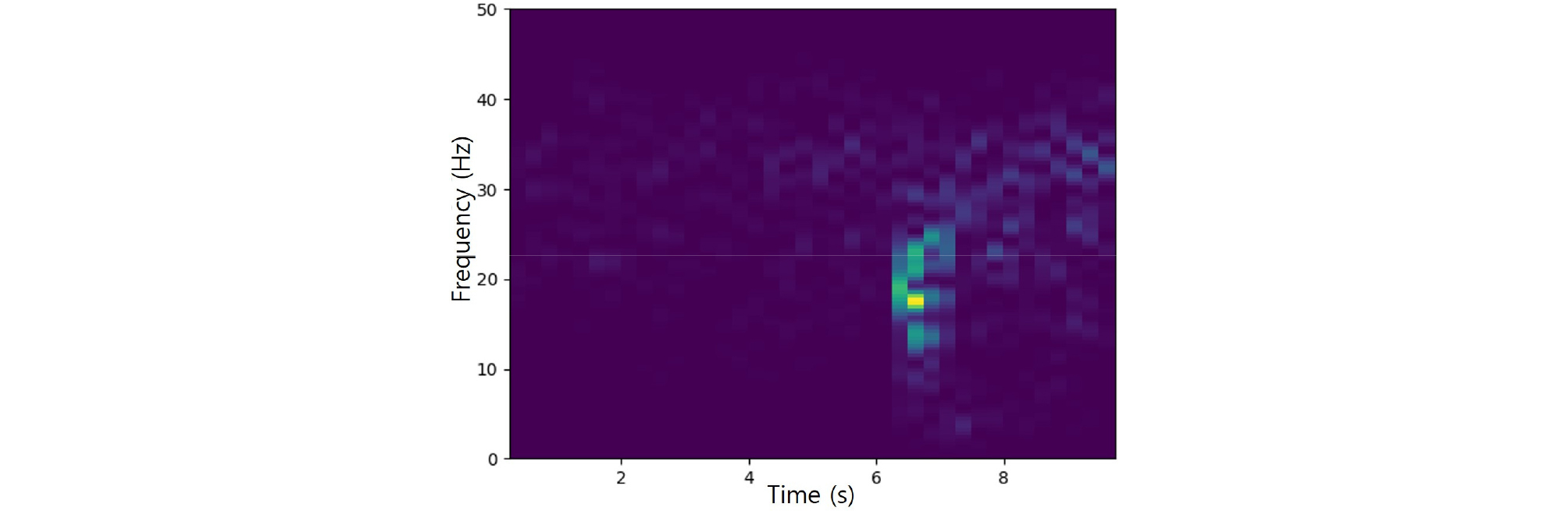
여기서 는 지진 데이터, 시간 , 주파수 , 지진 데이터의 길이 을 나타낸다. 본 논문에서는 윈도우 크기는 50 ms, 윈도우 중첩 크기는 25 ms, FFT Bin 수는 256으로 설정하였다. 생성된 스펙트로그램은 Fig. 2와 같이 지진파 신호를 시간에 따른 주파수의 변화를 파악할 수 있는 2차원 형태로 표현된다.
2.3 MEL-SPECTROGRAM
멜 스펙트로그램은 음성 신호 분야에서 널리 쓰이는 변환 방법으로, 스펙트로그램을 저주파 대역이 촘촘하게 설계된 멜 필터 뱅크에 통과시킴으로써 획득할 수 있다. 멜 필터 뱅크의 멜 단위는 스펙트로그램 주파수 단위 를 Eq. (4)와 같이 으로 변환하여 얻고, 역변환은 Eq. (5)와 같다. 멜 스펙트로그램은 Eqs. (6) ~ (10)과 같이 생성한다.
| $$m=2595\log_{10}(1+\frac f{700}).$$ | (4) |
| $$h=700(e^\frac m{1127}-1).$$ | (5) |
| $$MF[r]= \frac{1} {A _{r}} \sum _{k=L _{r}} ^{U _{r}} | V _{r} [k] \frac{ | X(t,k) | ^{2}} {N} |,$$ | (6) |
| $$A _{r} = \sum _{k=L _{r}} ^{U _{r}} | V _{r} [k] | ^{2},$$ | (7) |
| $$V_r\left[k\right]=\left\{\begin{array}{ll}0&k<f(r-1)\\\frac{k-f(r-1)}{f(r)-f(r-1)}&f(r-1)\leq k\leq f(r)\\\frac{f(r+1)-k}{f(r+1)-f(r)}&f(r)\leq k\leq f(r+1)\\0&k>f(r+1)\end{array}\right.,$$ | (8) |
| $$f(r)=floor((N+1)h(r)/Sampling\;Rate),$$ | (9) |
| $$Mel\;Spectrum=MF\lbrack r\rbrack,$$ | (10) |
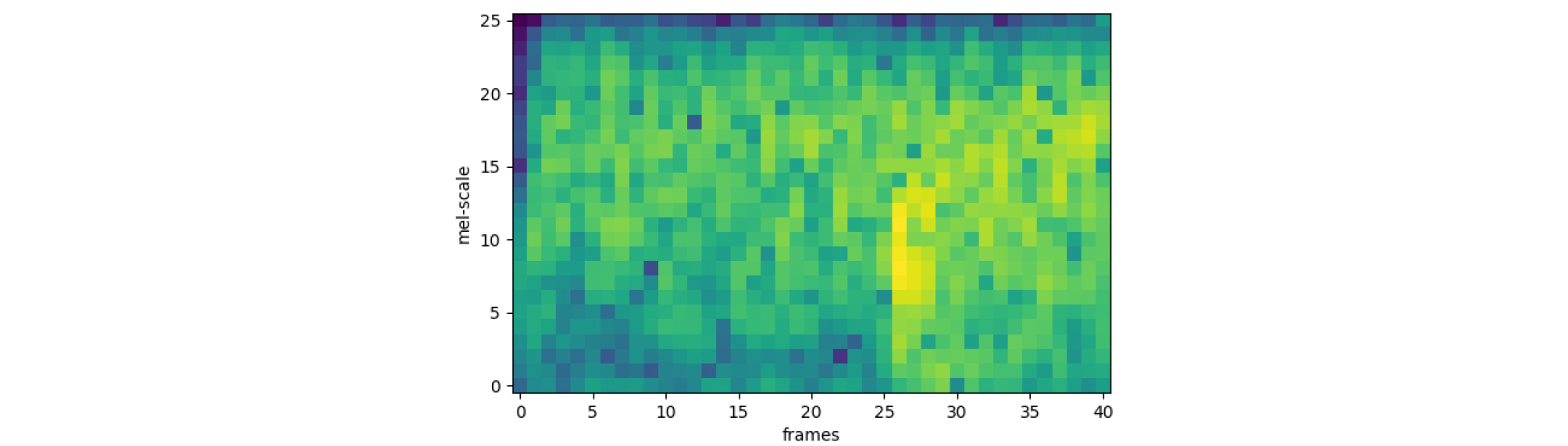
여기서 은 멜 필터 뱅크의 수, 는 시간, 는 주파수, 은 하한 주파수, 는 상한 주파수, 은 FFT Bin의 수를 나타낸다. 본 논문에서는 멜 필터 뱅크의 수는 26개, 하한 주파수는 0 Hz, 상한 주파수는 50 Hz, FFT Bin 수는 256으로 설정하였다. 이를 통해 26개의 멜 주파수 단위를 갖는 멜 스펙트로그램을 Fig. 3과 같이 생성한다.
III. 지진파 분류를 위한 특징 추출방법
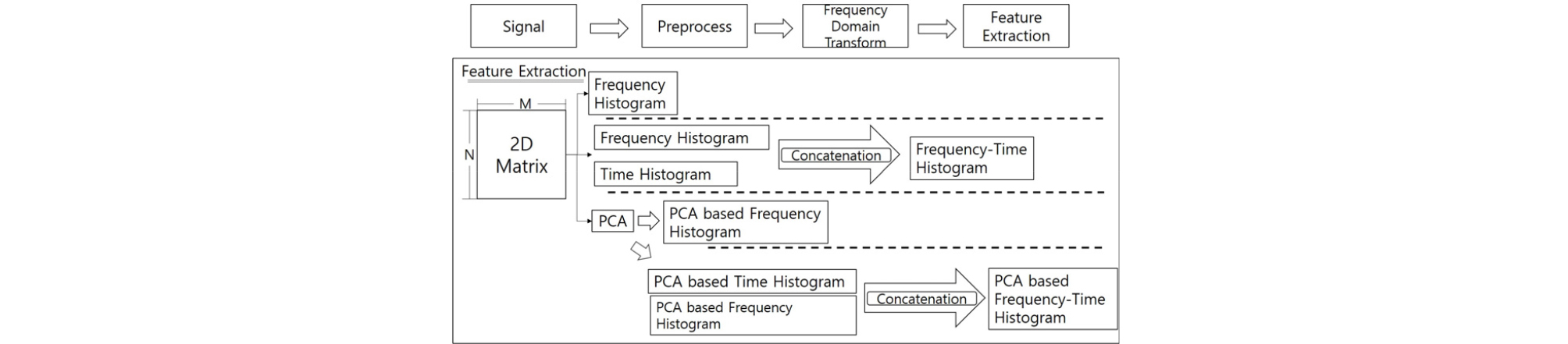
본 논문에서는 지진파 분류를 위해 스펙트로그램 및 멜 스펙트로그램 주파수-시간 공간에서의 특징 추출방식을 제안한다. Fig. 4와 같이 지진 신호는 전처리 및 주파수 변환 과정을 통과한 후 2차원 공간에서 특징 추출을 수행한다. 본 연구에서는 개별 주파수 및 시간 특징 추출 후 연결 특징 벡터를 생성하였으며, 이때 각각 히스토그램과 PCA 방법을 적용하는 기법을 제안하였다.
3.1 히스토그램 기반 주파수 특징 추출
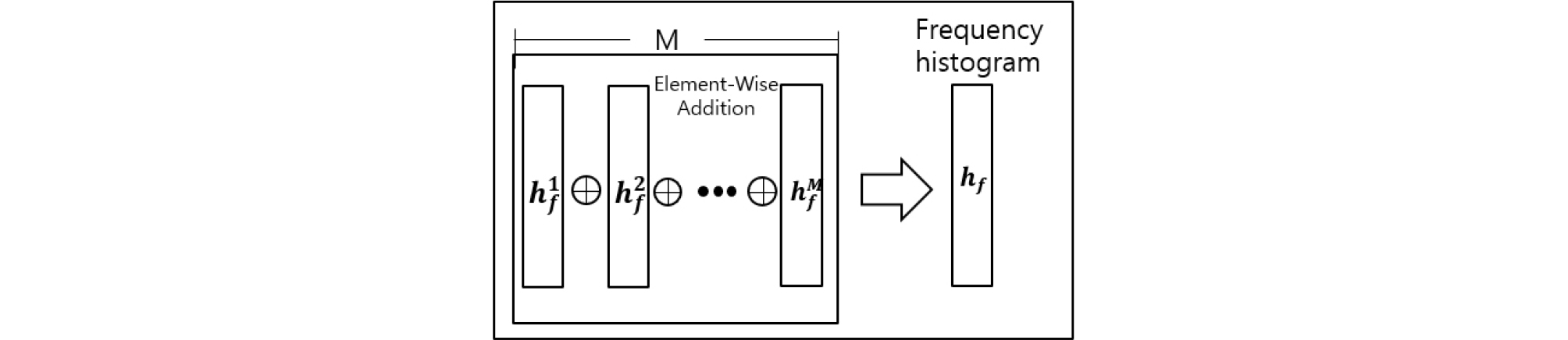
지진파 신호의 스펙트로그램 및 멜 스펙트로그램 은 Fig. 2와 Fig. 3과 같이 2차원 형태로 표현된다. Fig. 5와 같이 크기의 2차원 특징에서 주파수 히스토그램은 Eq. (5)와 같이 열벡터 을 이용하여 계산한다.
| $${\boldsymbol h}_{\mathbf f}=\sum_{c=1}^M\boldsymbol h_{\mathit f}^{\mathit c}.$$ | (11) |
3.2 히스토그램 기반 주파수-시간 특징 추출
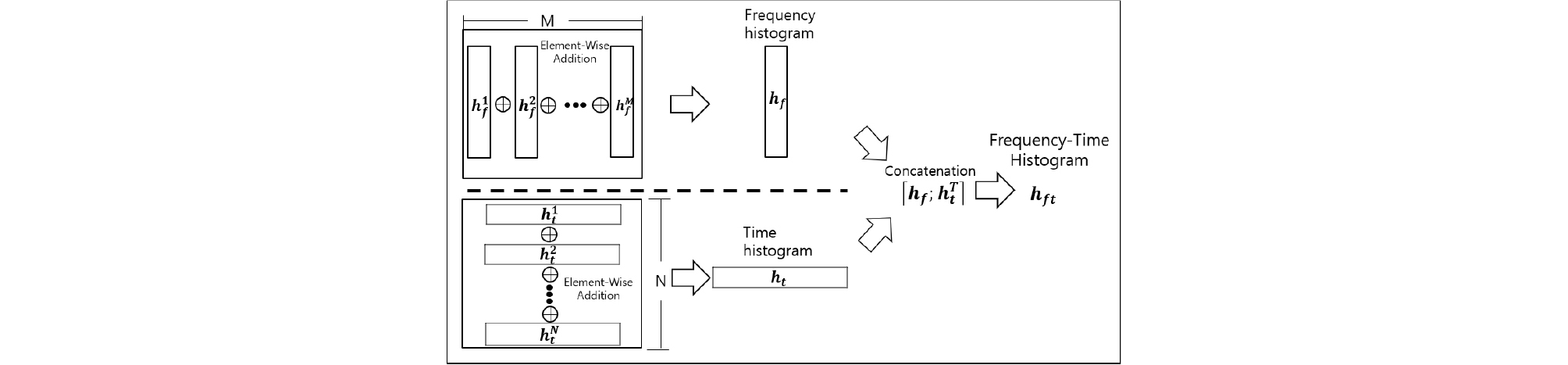
주파수 히스토그램의 경우 열벡터의 요소별 합으로 인해 시간에 관련된 정보를 특징 벡터에 반영하지 못하게 된다. 이러한 부분을 보완하기 위해 본 논문에서는 Fig. 6과 같이 주파수축 히스토그램 및 시간 축 히스토그램 특징을 추출 후 연결 벡터를 구성한다. 주파수축 히스토그램과 시간 축 히스토그램은 Eqs. (5)와 (6)과 같이 계산하며 Eq. (7)과 같이 연결 벡터를 구성한다.
| $${\boldsymbol h}_{\mathbf t}=\sum_{r=1}^N\boldsymbol h_{\mathit t}^{\mathit r},$$ | (12) |
| $${\boldsymbol h}_{\mathbf f\mathbf t}=\begin{bmatrix}{\boldsymbol h}_{\boldsymbol f\boldsymbol t}\\\cdots\\\boldsymbol h_{\mathit t}^{\mathit T}\end{bmatrix}.$$ | (13) |
3.3 PCA 기반 주파수 특징 추출
주파수 히스토그램 특징 추출에서는 열벡터 를 요소별 합을 통해 히스토그램 특징을 추출하였다. PCA 기반 주파수 특징 추출에서는 요소별 합 연산을 주성분 분석 기법으로 대체하여 데이터 표본 내의 합산이 아닌 주요 성분만을 추출하여 각 주파수의 대푯값으로 적용한다. 먼저 스펙트로그램과 멜 스펙트로그램을 주파수 축 Bin을 기준으로 나눈 을 구한다. 여기서 S는 총 표본 개수이고 N은 주파수 축 Bin 개수를 뜻한다. 는 Eq. (8)과 같이 표현되며 전치 연산을 나타낸다. 의 공분산 행렬은 Eq. (9)와 같이 평균 벡터 와 표본 개수 S를 통해 구한다.
| $$C_{f_i}=\frac1S\sum_k^S(A_{t_i}(k)-{\boldsymbol\mu}_{{\boldsymbol A}_{{\mathit t}_{\mathit i}}})(A_{t_i}(k)-{\boldsymbol\mu}_{{\mathit A}_{{\mathit t}_{\mathit i}}})^T.$$ | (15) |
본 연구에서는 공분산 행렬 에 고윳값 분해를 수행한 후 가장 큰 고윳값을 가지는 고유벡터 를 주요 성분으로 채택한다. 새로운 데이터가 입력되면 고유벡터 공간으로 정사영 된 주파수 i의 계수는 Eq. (10)과 같이 계산되며 PCA 기반 주파수 특징 추출은 Eq. (11)과 같이 구성된다.
| $$p_{f_i}^{}=({\boldsymbol v}_{{\boldsymbol f}_{\mathit i}})^T(\boldsymbol h_{\mathit t\mathit,\mathit t\mathit e\mathit s\mathit t}^{\mathit i})^T,$$ | (16) |
| $${\boldsymbol p}_{\mathit f}=\lbrack p_{f_1},\cdots,\;p_{f_N}\rbrack^T.$$ | (17) |
3.4 PCA 기반 주파수-시간 특징 추출
히스토그램 기반 주파수-시간 특징 추출과 같이 PCA 기반 특징 추출방식에서도 주파수 특징 추출방식을 주파수-시간 특징 추출방식으로 확장한다. PCA 기반 시간 특징 추출을 하기 위해 Eqs. (12)와 (13)과 같이 스펙트로그램 혹은 멜 스펙트로그램을 시간 축 Bin을 기준으로 한 j번째 시간의 데이터 행렬과 공분산 행렬로 표현한다.
| $$A _{f _{j}} = [ ( {h _{f}^{j,1}} ) ^{T},( {h _{f}^{j,2}} ) ^{T} ,\cdots ,( {h _{f}^{j,S}} ) ^{T} ],$$ | (18) |
| $$C_{t_j}=\frac1S\sum_k^S(A_{f_j(k)}-{\boldsymbol\mu}_{{\boldsymbol A}_{{\mathit f}_{\mathit j}}})(A_{f_j}(k)-{\boldsymbol\mu}_{{\mathit A}_{{\mathit f}_{\mathit j}}})^T.$$ | (19) |
PCA 기반 주파수 특징 추출과 같게 공분산 행렬 에 대한 고윳값 분해를 수행한 후 가장 큰 고윳값에 해당하는 고유벡터 를 주요 성분으로 채택한다. 새로운 데이터가 입력되면 고유벡터 공간으로 정사영 된 시간 j의 계수와 PCA 기반 시간 특징 추출은 Eqs. (14)와 (15) 같이 계산된다.
| $$p_{t_j}^{}=({\boldsymbol v}_{{\boldsymbol t}_{\mathit j}})^T\boldsymbol h_{\mathit f\mathit,\mathit t\mathit e\mathit s\mathit t}^{\mathit j}.$$ | (20) |
| $${\boldsymbol p}_{\boldsymbol t}=\lbrack p_{t_1},\;\cdots,\;p_{t_M}\rbrack^T.$$ | (21) |
PCA 기반 주파수-시간 특징 추출은 Eq. (16)과 같이 PCA 기반 주파수와 시간 특징값의 연결 특징 벡터를 통해 구성한다.
| $${\boldsymbol p}_{\boldsymbol f\boldsymbol t}=\begin{bmatrix}{\boldsymbol p}_{\boldsymbol f}\\\cdots\\\boldsymbol p_{\mathit t}^{\mathit T}\end{bmatrix}.$$ | (22) |
3.5 고주파 대역 필터를 통한 전처리
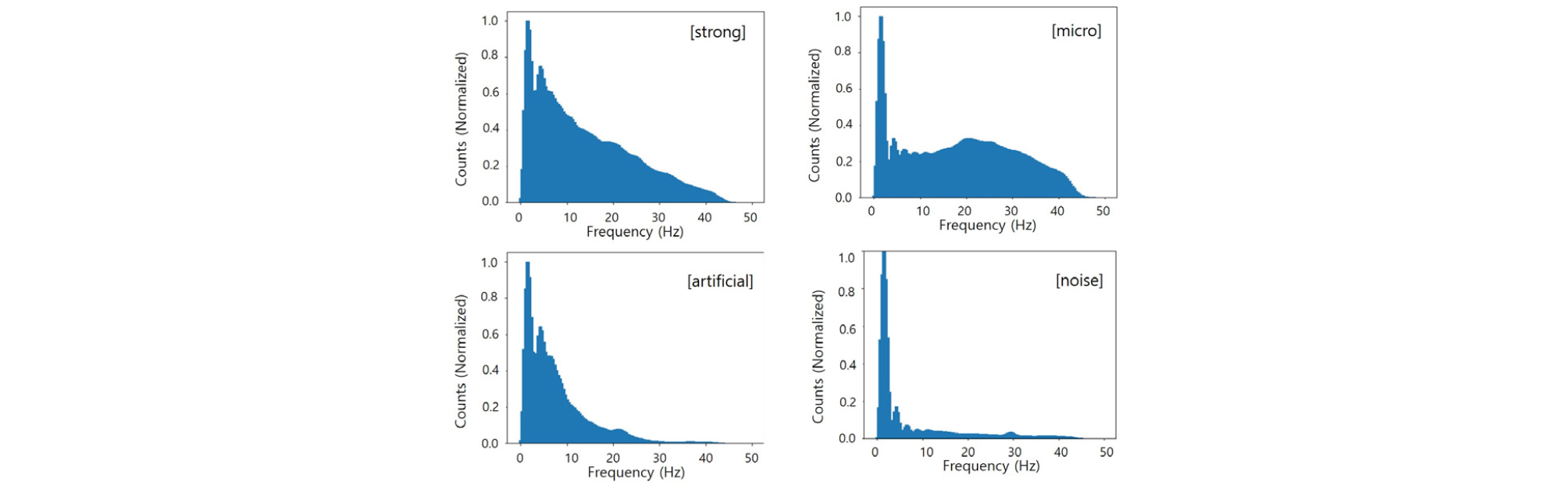
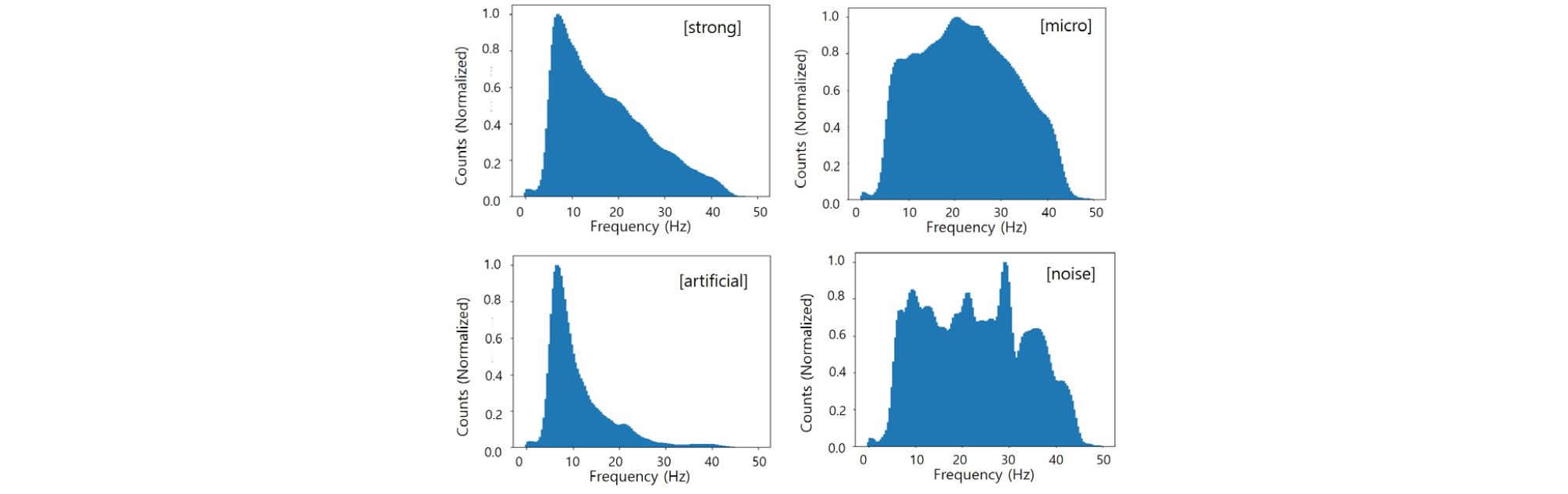
Fig. 7에는 원본 데이터의 주파수 영역 특징을 도시하였다. 그 결과 모든 이벤트의 0 Hz ~ 5 Hz 부근에서 유사한 주파수 특성을 나타낸다. 이러한 중첩된 주파수 특성은 지진파 분류문제에 있어 악영향을 미칠 수 있다. 따라서 본 연구에서는 특징 추출 전에 지진파 입력 데이터에 차단주파수가 5 Hz인 고주파 대역 필터를 적용하였다. 이를 통해 Fig. 8과 같이 이벤트별 히스토그램 형상의 구분 성이 향상될 수 있음을 확인하였다. 전처리에 따른 특징 추출 및 분류 성능은 모의실험 부분에서 비교 분석한다.
IV. 모의실험
본 모의실험에서는 2017년 1월 1일부터 2018년 7월 31일까지 대한민국에서 발생하는 지진 관측 데이터를 이용하였다. 모의실험에 이용되는 관측소 개수 및 지진 이벤트 수는 Table 1에 정리하였다.
Table 1. Number of events and seismological observatory.
| Type | Number of events | Number of stations |
| Strong earthquake | 295 | 250 |
| Micro earthquake | 461 | 671 |
| Artificial earthquake | 144 | 179 |
기상청에서 제공된 24시간 연속 지진 데이터와 지진 이벤트 목록 파일을 기반으로 지진 이벤트 및 잡음을 구성하였으며 100 Hz로 샘플링된 E, N, Z 채널 관측 데이터 중 Z 채널 데이터만을 이용하였다. 모의실험 데이터는 지진 이벤트 목록 파일에 기록된 P파 도착 시각을 기준으로 10 s간의 데이터를 추출하여 데이터 표본으로 사용하였다. 잡음의 경우 지진 발생 목록에 기록되지 않은 날짜에서 임의로 10초 구간의 표본을 추출하였다. 모의실험에 사용된 데이터셋은 Table 2와 같이 구성된다.
Table 2. Number of events for experiments.
| Dataset | Total | Number of details |
| strong-micro-artificial vs. noise | 8,647 | 3,278 / 5,369 |
| micro vs. noise | 5,160 | 1,720 / 3,440 |
| micro vs. artificial | 1,179 | 786 / 393 |
본 실험에서는 제안된 특징 추출의 효용성을 알아보기 위해 특징 추출 결과를 Radial Basis Function (RBF) Kernel을 적용한 SVM 분류기에 적용한 후 분류 성능을 토대로 제안한 특징과 히스토그램 주파수 특징을 비교 분석하였다.
분류 결과의 성능 측정은 Eqs. (17) ~ (19)와 같이 Accuracy, True Positive Rate(TPR), False Positive Rate (FPR)을 사용한다. 각 특징 추출을 적용한 분류 결과의 Accuracy, TPR 수치는 높을수록 FPR 수치는 낮을수록 적합하다 볼 수 있다.
| $$Accuracy=\frac{TP+TN}{TP+TN+FP+FN},$$ | (23) |
| $$TPR= \frac{TP} {TP+FN},$$ | (24) |
| $$FPR= \frac{FP} {TN+FP},$$ | (25) |
여기서 TN: True Negative, TP: True Positive, FN: False Negative, FP: False Positive를 나타낸다. Table 3은 변환 공간(spectrogram, mel-spectrogram), 전처리 유/무, 특징 추출방법에 따른 분류 성능 결과를 정리하였다.
Table 3. Classification Result using SVM. Accuracy (%) / TPR (%) / FPR (%)
4.1 전처리 유무에 따른 Spectrogram vs Mel- spectrogram 특징 성능 비교
스펙트로그램에 비해 멜 스펙트로그램 상에서의 특징 추출방식은 전반적으로 FPR 성능이 좋지 못한 모습을 보여주고 있다. 이러한 현상은 저주파 대역을 세밀하게 보는 멜 스펙트로그램의 성질에 기인한다. 본 실험에서 지진파와 잡음의 경우 저주파 대역에서 공통되는 특징적 요소들이 존재하며 저주파 대역을 강조한 멜 스펙트로그램 상에서 특징 추출의 경우 분류 성능 저하의 결과를 보여준다. 그러나 전처리 필터를 각 변환 공간에 적용한 결과를 살펴보면 다른 경향성을 나타낸다. 전처리를 적용한 스펙트로그램 상에서는 특징 추출방식에(주파수-시간 정보 특징 추출의 경우) 따라 분류 성능이 개선되는 모습을 보인 반면, 전처리를 적용한 멜 스펙트로그램에서는 주파수만 사용한 특징 추출방식에서 전처리유무에 따라 약간의 성능 감소가 발견되었고 이를 제외한 다른 방식에서는 전반적인 성능 개선이 나타났다. 전처리를 통해 저주파 대역의 클래스 간 공통 특징 정보 부분을 억제한 후 멜 변환을 하게 됨으로써 클래스 간 중첩 부분이 다소 감소하여 성능 개선의 결과를 나타내고 있다.
4.2 주파수 특징 vs 주파수-시간 특징 성능 비교
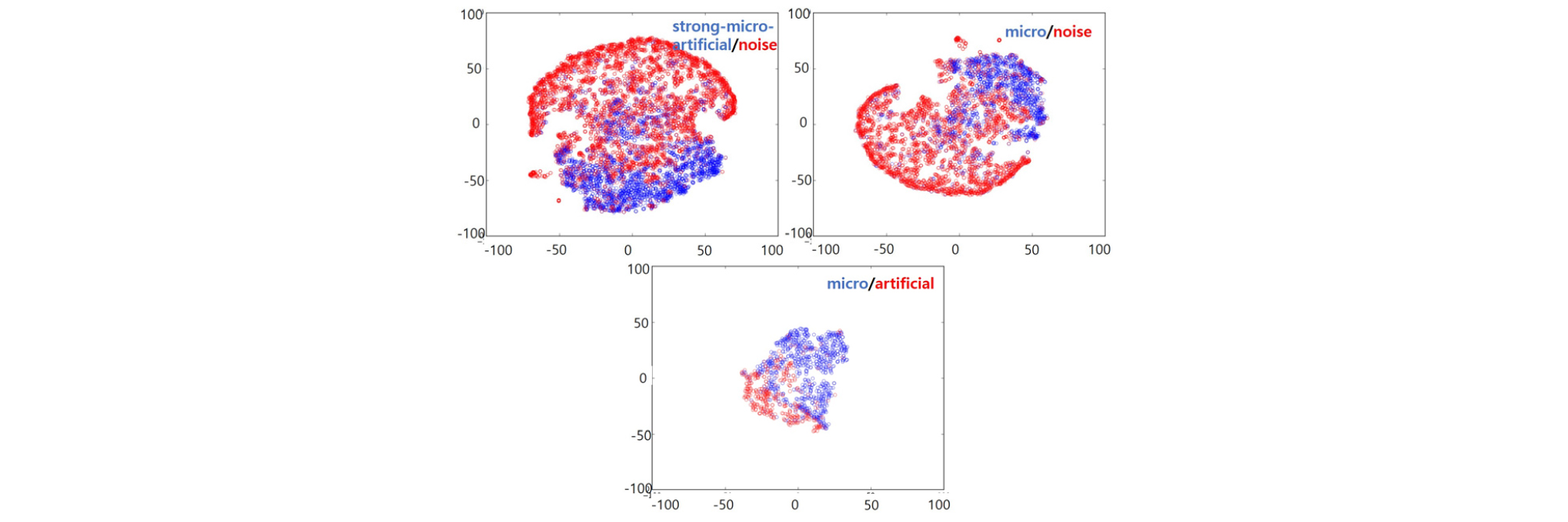
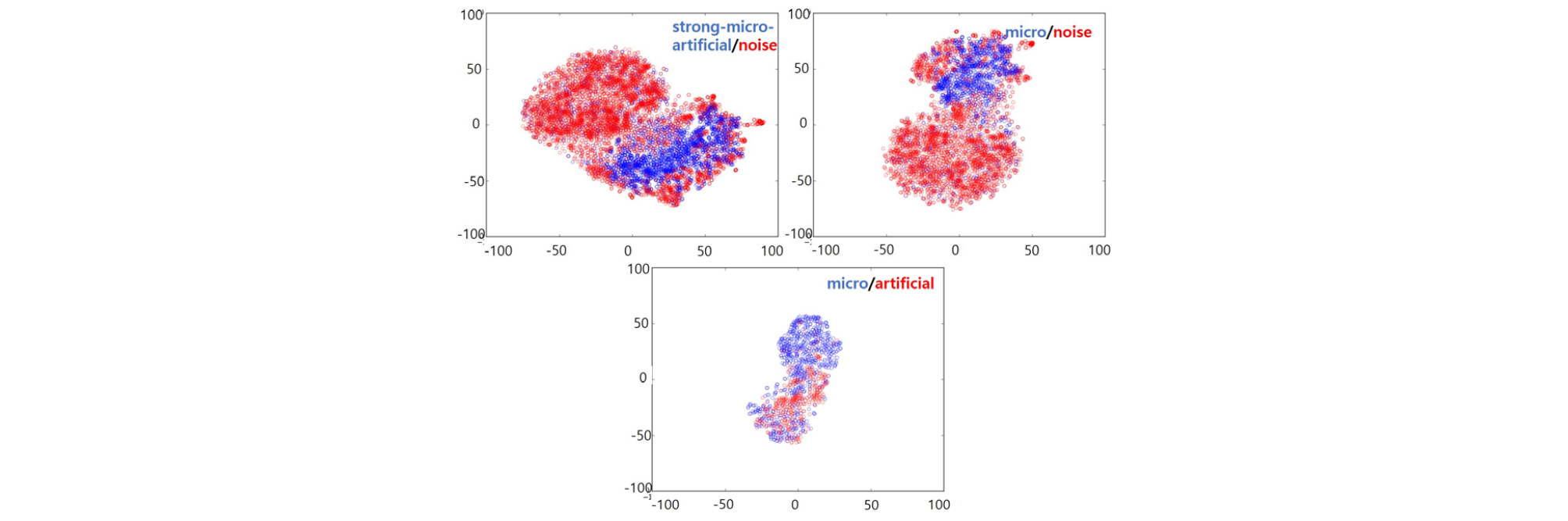
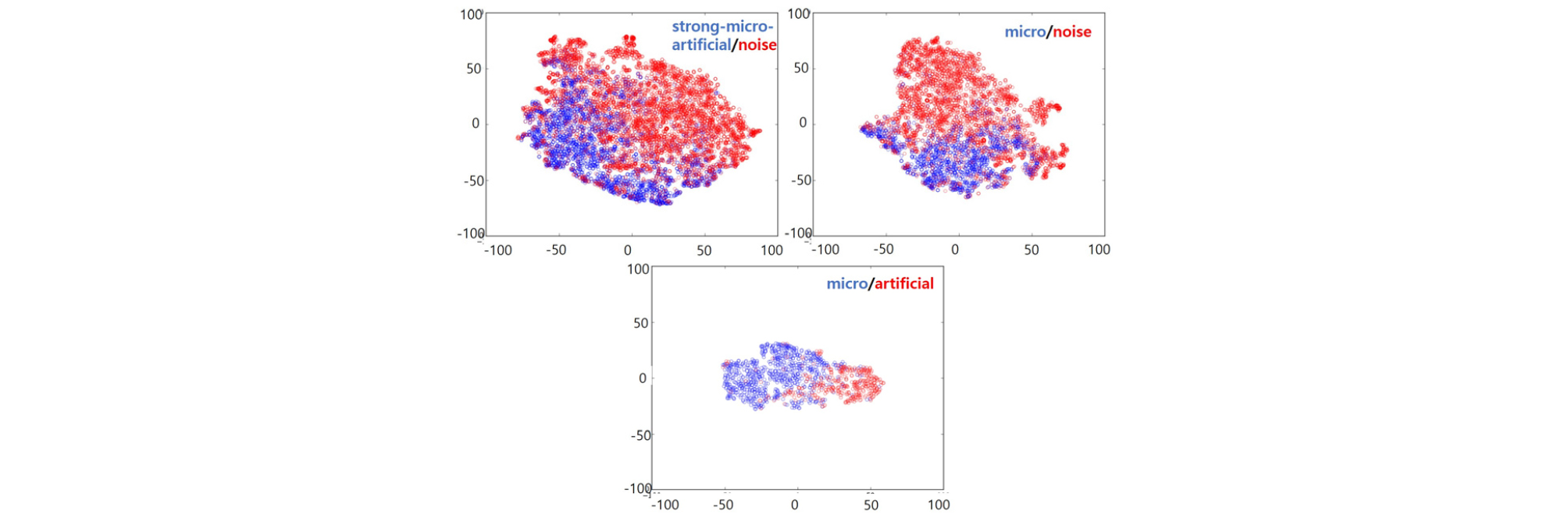
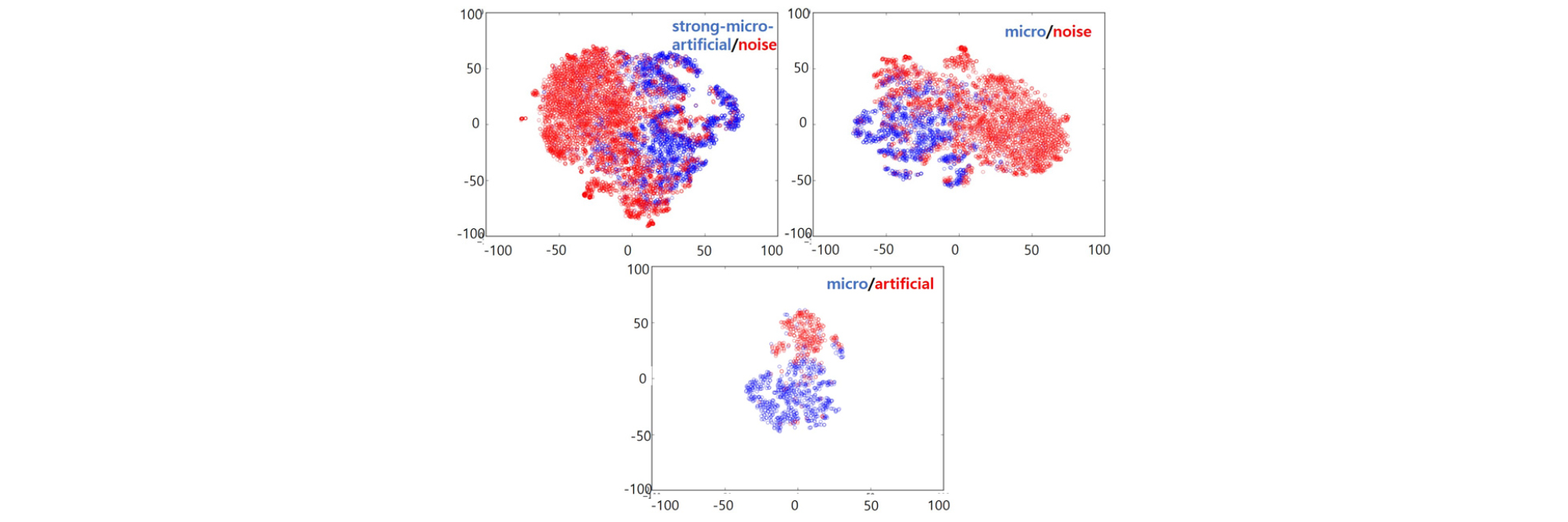
변환 공간에 따른 특징 추출방식의 비교는 Table 3의 결과를 기반으로 살펴보았다. 히스토그램 기반 주파수 특징 추출방식과 주파수-시간 특징 추출방식을 비교하면 전반적으로 주파수-시간 특징 추출방식이 향상된 분류 성능을 보이지만, PCA 기반에서는 전처리 여부에 따라 다른 결과를 보인다. 전처리를 적용한 경우 주파수-시간 특징 추출방식이 주파수 특징 추출방식보다 향상된 결과를 보였으나, 전처리를 적용하지 않는 경우 주파수-시간 특징 추출방식에서 성능이 저하된 결과를 보여주고 있다. 이는 PCA기반 특징을 Figs. 9 ~ 12의 특징 시각화로 분석하면 특징 추출방법과 전처리유무에 따른 차이로 인한 결과임을 확인할 수 있다. Figs. 9와 10은 전처리가 적용되지 않은 특징 추출방법으로 지진과 잡음을 분류하는 경우 주파수와 주파수-시간에서 다른 양상을 보인다. 주파수 특징에서는 지진 특징 분포와 잡음 특징 분포가 일정 부분 겹치면서 한쪽으로 치우쳐 있지만, 주파수-시간 특징에서는 지진 분포의 중심이 잡음 분포의 중심과 거리가 더 가까워진 모습을 확인할 수 있다. 미소지진과 잡음을 분류하는 경우와 미소지진과 인공지진을 분류하는 경우에서도 주파수만 사용하는 경우보다 주파수-시간에서 두 분포의 중심 거리가 가까워진 것을 확인할 수 있다. Figs. 11과 12는 전처리가 적용된 특징 추출방법으로 전처리가 적용되지 않은 특징 추출방법과는 다른 양상을 보인다. 지진과 잡음을 분류하는 경우 주파수 특징에서는 잡음 특징의 분포가 지진 특징의 분포와 크게 겹치는 모습을 보이지만, 주파수-시간 특징을 사용하는 경우 두 분포의 중심 거리가 멀어지고 겹치는 영역이 작아진 모습을 보인다. 미소지진과 잡음을 분류하는 경우에서도 주파수만 사용하는 경우보다 주파수-시간을 사용하는 경우 두 분포의 중심이 멀어지는 모습이 보이는 것을 확인할 수 있다. 미소지진과 인공지진을 분류하는 경우 주파수만 사용하는 경우보다 주파수-시간 특징에서 인공지진의 분포 크기가 작아지는 모습을 보였으나, 미소지진의 분포와 겹치는 부분도 늘어난 것을 확인할 수 있었다. 전처리 적용결과를 기반으로 살펴보면, 스펙트로그램 공간에서 주파수-시간 정보 방식의 경우 주파수 정보만을 이용한 방식에 비해 히스토그램 기반 특징 추출은 Accuracy가 평균적으로 6.34 % 향상되었으며 PCA 기반 특징 추출은 평균 2.41 %의 향상된 결과를 보여주었다. 지진 신호 분류 시 주파수 성분만을 이용한 한계를 보이며, 시간에 따른 지진 신호의 특성 요소가 반영됨으로써 성능 향상을 보여주고 있다.
4.3 히스토그램 기반 특징 vs PCA 기반 특징 성능 비교
전처리 적용 변환 공간에서 히스토그램과 PCA 기반 특징 방식을 비교해보면 전반적으로 PCA 기반 특징 추출방식이 우수한 성능을 확인하였다. 스펙트로그램 공간에서 주파수-시간 특징 추출 결과들을 비교해보면 히스토그램은 평균 90.93/14.34(Accuracy/FPR)의 성능을 보였으나 PCA는 평균 93.34/7.34(Accuracy/ FPR)의 향상된 분류 결과를 보였다. 주파수 정보만을 이용한 PCA 기반 주파수 특징은 히스토그램 기반 주파수-시간 특징보다 FPR 측면에서는 우수한 모습을 보이기도 하였으나 가장 우수한 성능을 보여주는 특징은 스펙트로그램에서 PCA 기반 주파수-시간 특징 추출방식이었다. 저주파 구역에서 지진 신호와 잡음의 중첩된 특성들로 인해 히스토그램 방식 주파수-시간 특징 추출의 경우 스펙트로그램(전처리 적용)보다 멜 스펙트로그램(전처리 적용) 상에서의 분류 성능이 우수한 성능을 나타내고 있다. 하지만 PCA 기반 방식에서는 주요 성분을 추출하는 과정으로 인해 저주파를 강조한 멜 스펙트로그램보다는 모든 주파수 영역 대를 고르게 살펴보는 스펙트로그램 상에서의 시간-주파수 특징 추출방식이 향상된 결과를 나타내었다.
V. 결 론
본 논문에서는 지진파 분류를 위한 주파수-시간 공간상의 히스토그램 기반 특징 추출방식과 주성분 기반 특징 추출방식을 제안하였다. 제안된 각 방식에서 주파수 정보와 더불어 시간 정보를 연결하는 방식으로 특징 벡터를 구성하였다. 모의실험 결과 주파수 히스토그램 특징 방법의 경우 시간에 따른 변화 정보를 반영하지 못함으로써 지진파 분류 성능 저하의 모습을 보였으나 제안된 시간-주파수 특징 추출방식의 경우 주파수 정보만을 사용한 방식보다 평균적으로 약 4 % 정도의 Accuracy 향상률을 나타내었다. 또한, 히스토그램 특징 추출방식보다 PCA 기반 특징 추출방식이 높은 분류 정확도와 낮은 오 분류 결과를 보여주었다.