I. 서 론
II. 데이터 병렬화
2.1 Synchronous SGD
2.2 Asynchronous SGD
III. 모델 병렬화
IV. 연산량 및 통신량 분석
4.1 연산량 분석
4.2 통신량 분석
V. 결 론
I. 서 론
딥러닝은 심층 신경망(Deep Neural Network, DNN)을 빠르게 학습시킬 수 있는 방법[1,2]이 제안되면서 급속도로 발전해왔다. DNN은 음성 인식이나 이미지 인식과 같은 분류 문제에서 우수한 성능을 보여주고 있다.[3,4] 또한, 생성 모델(generative model)[5,6]을 이용한 이미지 생성이나 음성 변환과 같은 다양한 응용 분야에 적용되고 있다. 많은 딥러닝 응용 분야의 공통점은 대규모 데이터를 사용하여 학습시키는 경우 더 좋은 성능을 보인다는 것이다. 또한, DNN 모델의 깊이가 깊을수록, 즉 층의 개수가 많을수록, 그 성능이 향상되는 경향이 있다.[3,7] 대규모의 DNN 모델과 대량의 학습 데이터에 의해서 필연적으로 DNN 학습에 오랜 시간이 소요되기 때문에, 고속 학습을 위한 병렬 처리 알고리즘들이 연구되어 왔다.
현재 가장 널리 사용되고 있는 DNN 학습 방법은 Contrastive Divergence(CD)[1,2]를 이용한 사전 학습방법과 오류 역전파(error back propagation: EBP)[8]를 이용한 학습 방법으로, PyTorch,[9] Tensor Flow,[10] Kaldi[11]등 최근 널리 사용되는 공개 소프트웨어들에서 기본적으로 지원하고 있다. 이 두 가지 학습 방법은 손실 함수만 다를 뿐, gradient descent 방식으로 모델 파라미터(즉 DNN의 weight)를 최적화한다. Batch gradient descent라고도 불리는 원래의 gradient descent 방식[8]에서는 전체 학습 데이터를 이용하여 gradient를 계산한 후 모델 파라미터를 갱신하는 과정을 반복한다. Batch gradient descent는 다음 절에서 설명할 데이터 병렬화 기법을 사용한 병렬 처리가 가능하지만, 많은 local minima를 가지는 DNN의 학습에는 적당하지 않다.[12]
Stochastic Gradient Descent(SGD)에서는 전체 학습 데이터를 이용하여 정확한 gradient를 구하는 대신에 각 학습 샘플마다 gradient를 구하고 모델 파라미터를 갱신하는 과정을 반복한다.[13] 이것은 일종의 random walk 현상을 제공하여 local minima를 탈출하는 효과가 있기 때문에 DNN 학습에 상대적으로 유리하다.[12] 하지만 SGD는 순차적으로 동작하기 때문에 병렬화하기 어려워서 학습 시간이 오래 걸린다는 단점이 있다.
Batch gradient descent와 stochastic gradient descent를 절충한 mini-batch stochastic gradient descent 방식은 전체 학습 데이터를 mini-batch라고 불리는 여러 개의 작은 그룹으로 나누고, 하나의 mini-batch에 속한 모든 데이터를 이용하여 gradient를 구하고 모델 파라미터를 수정하는 과정을 반복한다. Mini-batch 간에는 순차적으로 수행되지만, mini-batch 내부에서는 Graphics Processing Unit(GPU) 등을 사용하여 batch gradient descent와 유사한 방법으로 병렬화함으로써 수행 속도를 향상시킬 수 있기 때문에 현재 가장 널리 사용되고 있는 DNN 학습 방법이다. 그러나 병렬화 효율을 높이기 위해서 mini-batch의 크기를 늘리면 random walk 효과가 줄어들어 학습이 어려워진다는 단점이 있다. 즉, 병렬화 효율이 제한적이다.[14] 본 논문에서는 mini-batch SGD를 추가적으로 병렬화하는 방법들을 소개한다. 수식 표현과 설명의 간략화를 위해서 알고리즘은 SGD를 기준으로 설명하지만, 이후에 나오는 모든 SGD는 mini-batch SGD를 의미한다.
SGD 알고리즘은 다음과 같이 손실 함수의 gradient 반대 방향으로 DNN의 weight를 조금씩 수정하면서 학습을 진행한다.
여기서 는 weight, 는 learning rate, 은 손실 함수, 는 입력 데이터, 는 심층 신경망이 출력해야 하는 목표 값이고, 첨자 는 반복 횟수(즉 mini-batch 인덱스)를 나타낸다. 반복적 수행이 필요한 SGD 기반의 최적화 알고리즘은 순차적으로 진행되기 때문에 병렬화하기 어렵다. 따라서 SGD 기반의 병렬 학습 알고리즘은 다양한 근사방법을 사용한다. 이러한 근사 방법들은 SGD에서 필요한 gradient 값을 근사적인 방식으로 구하는데, 이러한 근사 gradient의 영향을 최소화할 필요가 있다. 본 논문에서는 기존의 SGD 기반 DNN 병렬 학습 알고리즘을 소개하고 연산량, 통신량, gradient 근사 방법 등을 분석한다.
일반적으로 병렬화 방법은 데이터 병렬성을 활용한 방법과 모델 병렬성을 활용한 방법으로 분류할 수 있다. II장에서는 데이터 병렬화 기반의 DNN 학습 알고리즘을 소개하고, III장에서는 모델 병렬화 기반의 DNN 학습 알고리즘을 소개한다. IV장에서는 각 병렬 학습 알고리즘의 연산량과 통신량을 분석하고, V장에서 결론을 맺는다.
II. 데이터 병렬화
데이터 병렬화는 데이터를 나누어 동시에 수행하는 것이다. 일반적으로 데이터 병렬화 기반 DNN 학습에는 마스터 모델 파라미터를 관리 및 저장하는 파라미터 서버와 마스터 모델 파라미터의 사본과 학습 데이터 일부를 전송받아서 gradient를 계산하는 컴퓨팅 노드들이 필요하다. 여기서 컴퓨팅 노드란 하드웨어 구성에 따라서 GPU 또는 Central Processing Unit(CPU) 코어 등이 될 수 있다. 전체 학습 데이터를 컴퓨팅 노드 개수로 나눈 일부 학습 데이터와 DNN 모델 파라미터를 모든 컴퓨팅 노드에 전송하고, 각 컴퓨팅 노드에서는 서로 다른 학습 데이터를 사용하여 동시에 학습한다. 각 컴퓨팅 노드의 DNN은 서로 다른 데이터를 사용하여 학습하기 때문에 결과적으로 서로 다른 지역 모델 파라미터 값을 갖게 되는데, 이러한 지역 모델 파리미터들, 즉 지역 DNN 모델의 weight들을 통합하여 하나의 마스터 모델을 만들어야 한다. 모든 컴퓨팅 노드의 지역 모델을 통합하여 마스터 모델을 만드는 방법에는 동기식(synchronous) 방식과 비동기식(asynchronous) 방식이 있다. 2.1절에서 synchronous SGD 방법을 설명하고, 2.2절에서 asynchronous SGD 방법을 설명한다.
2.1 Synchronous SGD
Synchronous SGD는 일정 시점에서 모든 컴퓨팅 노드의 모델 파라미터를 조합하여 마스터 모델 파라미터를 만든다(Fig. 1). 가장 간단한 조합 방법은 다음과 같이 모든 지역 모델 파라미터를 평균하여 마스터 모델 파라미터를 구하는 것이다.[15]
여기서 는 마스터 모델 파라미터이고, 는 번째 컴퓨팅 노드의 지역 모델 파라미터이다. DNN weight 대신에 gradient를 전송해서 마스터 모델 파라미터를 구할 수도 있다. 갱신된 마스터 모델이 다시 각 컴퓨팅 노드에 배포될 때 모든 지역 모델은 동일한 파라미터 값을 갖게 된다. 컴퓨팅 노드의 지역 모델 파라미터를 조합하는 방법과 빈도에 따라서 여러 가지 변형된 방법이 존재한다.
SimuParallelSGD[15]는 각 컴퓨팅 노드가 독립적으로 SGD를 수행하고 최후에 한 번 마스터 모델 파라미터를 생성하는 방법이다. 반면에 Bulk-Synchronous Parallel(BSP)[16]은 각 컴퓨팅 노드에 할당된 하나의 mini-batch에 대한 gradient 계산을 마칠 때마다 모든 컴퓨팅 노드의 gradient를 평균하여 마스터 모델을 갱신한다. 이것은 결과적으로 mini-batch 크기를 배 증가하여 학습하는 것이 된다.
Mini-batch 크기를 고려해서 동기화 주기를 결정할 수도 있다.[17] 즉, 번째 mini-batch 학습 후 동기화를 수행되게 하고, 수렴 속도를 고려하여 를 최적화한다. 동기화에는 통신이 수반되기 때문에 동기화 주기 최적화 시 통신 비용도 함께 고려해야 한다. 이렇게 번째 mini-batch마다 동기화를 수행하는 것은 BSP와 다르게 실질적인 mini-batch 크기를 증가하는 효과가 있는 것은 아니다. 즉, hypothesis space에서 개별적으로 학습된 지역 모델 파라미터의 조합[18]으로 마스터 모델 파라미터를 주기적으로 갱신하는 것으로서, 지역 모델 파라미터들의 평균을 이용하는 방법 외에도 파라미터마다 가중치를 부여하는 등의 여러 가지 조합 방법이 가능하다.
Elastic averaging SGD(EASGD)[19]에서는 각 지역 모델 파라미터가 개별적으로 유지되지만 마스터 모델 파라미터로부터 멀어질 수 있는 정도가 제어된다. Block-wise Model-Update Filtering(BMUF)[20]에서는 이전 마스터 모델 파라미터와 현재 지역 모델 파라미터 평균의 차이를 마스터 모델 파라미터 변화량으로 간주하고 모멘텀을 추가하여 마스터 모델 파라미터를 갱신한다. Sandblaster L-BFGS[21]에서는 각 컴퓨팅 노드에서 전송받은 gradient를 사용하여 limited- memory Broyden Fletcher Goldfarb Shanno(L-BFGS) 알고리즘으로 분산되어 있는 마스터 모델의 파라미터를 갱신한다.
많은 컴퓨팅 노드를 사용하는 경우 일부 컴퓨팅 노드의 일시적인 통신장애 발생과 같은 예기치 못한 상황으로 전체 동기화 속도가 느려질 수 있다. 이러한 문제를 해결하기 위해서 Sync-SGD[22]에서는 개 이상의 컴퓨팅 노드를 할당한 후 개의 컴퓨팅 노드에서 gradient 계산이 끝나면 나머지 컴퓨팅 노드를 기다리지 않고 동기화를 진행한다. 동기화에서 배제된 컴퓨팅 노드에 할당된 학습 전체가 데이터가 학습에 사용되지 못하는 문제를 완화하기 위해서 각 컴퓨팅 노드는 매번 전체 학습 데이터에서 무작위로 mini-batch를 선택하여 컴퓨팅 노드 간에 사용하는 데이터에 중복이 발생할 수 있도록 한다.
2.2 Asynchronous SGD
Asynchronous SGD는 각 컴퓨팅 노드의 지역 모델 파라미터를 비동기적으로 수집하여 마스터 모델 파라미터를 갱신하는 방법으로서(Fig. 2), synchronous SGD에 비해서 마스터 모델 파라미터 갱신을 위한 동기화 비용이 적고, 상대적으로 느리거나 고장난 컴퓨팅 노드를 기다릴 필요가 없기 때문에 DNN 학습에 가장 널리 사용되는 병렬 학습 방법 중에 하나이다.[21]
Hogwild[23]에서는 공유 메모리에 저장된 마스터 모델 파라미터를 여러 프로세서가 비동기적으로 갱신한다. 이와 유사하게, HogBatch[24]에서는 mini-batch에 대한 gradient를 계산한 후 공유 메모리에 저장된 마스터 모델 파라미터를 비동기적으로 갱신한다. AsySVRG[25]에서는 SGD의 분산을 줄여서 학습 속도를 향상시킨 Stochastic Variance Reduced Gradient(SVRG)를 사용하여 공유 메모리 환경에서 비동기적으로 병렬화하였다.
Downpour SGD[21]에서는 여러 대의 파라미터 서버에 마스터 모델 파라미터가 나뉘어 저장되고 각 컴퓨팅 노드는 파라미터 서버들과 비동기적으로 통신한다. 따라서 하나의 파라미터 서버를 사용하는 것보다 통신의 병렬화 효과가 높아질 수 있다. Downpour SGD의 컴퓨팅 노드는 다음 장에서 설명할 모델 병렬화가 가능한 DistBelief[21]를 활용하기 때문에 하나의 컴퓨팅 노드가 실제로는 여러 개의 CPU 코어로 이루어질 수 있다.
Asynchronous decentralized parallel SGD(AD-PSGD)[26]에서는 마스터 모델을 관리하는 파라미터 서버가 없고 컴퓨팅 노드들이 그래프 구조로 연결되어 있다. 각 컴퓨팅 노드는 각자의 mini-batch 데이터를 이용해서 gradient를 계산한 후 지역 모델 파라미터를 갱신한다. 동시에 각 컴퓨팅 노드는 무작위로 선택된 인접 컴퓨팅 노드의 지역 모델 파라미터와 조합하여 파라미터를 동기화한다. 이렇게 하면 다수의 컴퓨팅 노드가 동시에 파라미터 서버와 통신해야 하는 상황이 발생하지 않기 때문에 통신 병목 현상이 감소된다. 학습이 종료되면 모든 컴퓨팅 노드의 지역 모델 파라미터를 평균해서 마스터 모델 파라미터를 구한다.
Asynchronous SGD에서는 컴퓨팅 노드들이 파라미터 서버에게 gradient를 비동기적으로 전송하기 때문에 먼저 도착한 gradient 순으로 마스터 모델 파라미터에 적용된다. 늦게 도착한 gradient는 그 gradient를 계산하기 위해서 사용된 마스터 모델 파라미터가 아니라 먼저 도착한 gradient에 의해서 이미 갱신된 마스터 모델 파라미터에 적용되기 때문에 문제가 발생할 수 있다. 이러한 gradient를 delayed gradient 또는 stale gradient라 하고, stale gradient 계산에 사용된 모델 파라미터를 stale weight라고 한다.
이러한 문제를 해결하기 위하여 stale gradient를 이용하여 현재 마스터 모델 파라미터를 갱신하는 것은 과거 마스터 모델 파라미터로부터 유도된 gradient를 사용하는 것이기 때문에 일종의 momentum으로 간주할 수 있다고 가정하고 momentum 가중치를 실험적으로 최적화하였다.[27] Stale gradient 문제 해결을 위한 또 다른 연구에서는 Taylor expansion을 이용하여 stale gradient 값을 보정함으로써 현재 마스터 모델 파라미터의 gradient 값을 예측하는 방법도 제안되었다.[28]
Downpour SGD에서는 마스터 모델 파라미터가 여러 파라미터 서버에 분산되어 저장되고 컴퓨팅 노드들과 비동기 및 병렬로 통신하기 때문에 stale gradient 이외에 일관성이 없는 마스터 모델 파라미터가 생성되는 문제가 추가적으로 발생할 수 있다.
III. 모델 병렬화
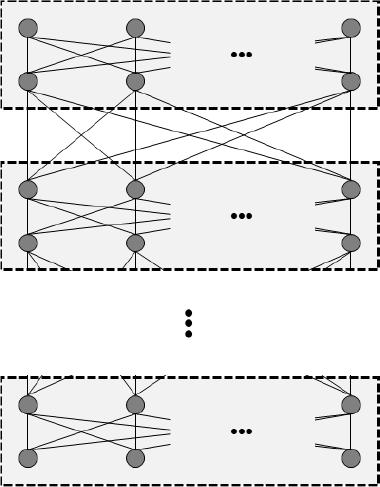
모델 병렬화는 모델을 나누어 동시에 수행하는 것이다. 모델 병렬화 기반 DNN 학습에서는 뉴런들을 여러 컴퓨팅 노드에 분산 배치함으로써, 나뉘어진 모델의 뉴런들이 여러 컴퓨팅 노드에서 동시에 계산에 참여할 수 있게 한다(Fig. 3). 예를 들어 Convolutional Neural Network(CNN)의 경우 필터들이 여러 컴퓨팅 노드에 분산되어 동시에 convolutin 연산을 수행할 수 있다.[29] 각 뉴런 출력값과 출력층으로부터 뒤로 전파되는 오류값은 컴퓨팅 노드 간의 통신망을 통하여 전달된다. 생물학적 신경망과 같이 모든 뉴런들이 동시에 계산에 참여할 수 있기 때문에 이론적으로는 병렬성이 높지만, 컴퓨팅 노드 간의 통신 비용 때문에 DistBelief[21]와 같은 범용 컴퓨팅 환경에서는 병렬화 효율에 한계가 있다. 또한, DNN의 학습 과정이 근본적으로 feed-forward(forward pass)와 오류 역전파의 순차적 반복이기 때문에 임의로 뉴런들을 분산 배치할 경우 모든 뉴런이 동시에 작업할 수 없는 경우가 생겨서 연산 자원이 비효율적으로 사용될 가능성이 있다.
Pipelined 병렬화 방식[30]은 DNN의 층 단위로 모델을 분산하는 모델 병렬화의 일종이다(Fig. 4). 즉, 같은 층에 속한 뉴런은 같은 컴퓨팅 노드에 할당한다. 첫 번째 컴퓨팅 노드에 할당된 층에서 번째 mini- batch의 forward pass를 마치면 다음 컴퓨팅 노드에 할당된 층에서 번째 mini-batch의 forward pass를 진행한다. 이때, 첫 번째 컴퓨팅 노드는 번째 mini- batch의 forward pass를 동시에 진행한다. 유사하게 backward pass도 각각 다른 mini-batch에 대하여 모든 컴퓨팅 노드가 동시에 진행한다(Fig. 5). 따라서 pipelined SGD에서는 모든 컴퓨팅 노드가 효율적으로 운영되며, DNN 모델 파라미터가 분산되어 메모리가 효율적으로 사용되기 때문에 대규모 DNN 학습에 적합하다. 그러나, 어떤 컴퓨팅 노드에 backward pass에 의해서 오류가 역전파되었을 때, 그 컴퓨팅 노드의 forward pass 값과 weight는 이미 다른 mini-batch에 의해서 변경되었기 때문에 잘못된 forward pass 값과 weight를 사용하는 delayed gradient 문제가 발생한다.
이러한 delayed gradient 문제를 해결하기 위하여 delay gradient를의 영향이 기존 SGD 대신에 mini- batch SGD를 수행하였을 때의 효과와 유사하다고 가정하고 mini-batch의 크기를 줄여서 delayed gradient의 영향을 감소시키는 방법[31]이 제안되었으나, mini- batch에 의한 병렬성 또한 줄어들기 때문에 일반적인 해결책은 아니다.
Decoupled parallel backpropagation using delayed gradient(DDG)[32]는 forward pass는 순차적으로 진행하고 backward pass만 pipeline으로 병렬화하는 방법이다. Forward pass를 순차적으로 진행함으로써 각 컴퓨팅 노드에 할당된 층의 입력 및 출력값은 정확한 값을 사용할 수 있다. 그러나, backward pass는 pipeline 방식으로 동시에 진행하기 때문에 delayed gradient를 사용하게 된다. 컴퓨팅 노드의 개수가 많을수록 delayed gradient의 영향이 커지기 때문에 병렬화 성능 향상에 한계가 있다.
Features replay[33]에서는 정확한 gradient 값과 delayed gradient 값의 차이를 loss 함수로 정의하고 현재 forward pass 값 대신에 지연된 forward pass 값을 사용하여 loss 함수를 최소화시키는 알고리즘을 제시하였다. 이와 유사하게, Decoupled Neural Interface(DNI)[34]에서는 각 층이 독립적이라고 가정하여 현재 층의 forward pass 값만으로 근사 gradient를 구하고 실제 gradient와의 차이가 적어지도록 recurrent neural network(RNN)에 적용하였으나, 근사 gradient 사용으로 인한 성능의 한계가 있다.
SpecTrain[35]에서는 momentum을 이용하여 미래의 weight 값을 추정하고 이를 forward pass에서 사용함으로써 backward pass 시에 delayed gradient가 발생하지 않도록 하였다. 그러나, 컴퓨팅 노드의 개수가 늘어날수록 추정된 미래 weight가 부정확지는 문제가 발생할 수 있다.
GPipe[36]에서는 mini-batch를 세분한 micro-batch 수준에서 forward pass를 모두 pipeline으로 수행한 후 backward pass를 pipeline으로 수행함으로써 delayed gradient 문제를 해결하고 기존의 SGD와 동일한 수행 결과를 얻을 수 있도록 하였다. 하지만, forward pass가 모두 끝난 후에 backward pass가 시작되기 때문에 mini-batch의 크기와 컴퓨팅 노드 수에 따라서 병렬화 효율성이 저하될 수 있다는 단점이 있다.
Delayed gradient 문제를 완전하게 해결하기 위한 방법으로 컴퓨팅 노드마다 delayed gradient의 시간 지연이 발생한 횟수만큼 모델 사본을 유지하고 backward pass 시에 forward pass에서 사용한 모델 파라미터를 갱신하는 방법이 있다(Fig. 6).[37,38] 즉, 컴퓨팅 노드는 여러 시간대의 모델 파라미터를 유지하고, 역전파된 delayed gradient에 알맞은 시간대의 모델 파라미터를 갱신한다. 이 경우 컴퓨팅 노드에는 여러 시간대의 모델이 존재하는데, Fig. 7에서 볼 수 있듯이 각각 다른 데이터를 사용하여 정확한 SGD 알고리즘이 각 시간대의 모델에 적용된다. 결과적으로, 이 방법은 모델 병렬화를 하였지만 데이터 병렬화가 된 경우이기 때문에 모델 파라미터 동기화가 필요하게 된다. 총 개의 컴퓨팅 노드로 구성된 시스템에서 여러 시간대의 모델을 유지하기 위해서 개의 모델 사본을 만들기 때문에, 결과적으로 synchronous SGD와 마찬가지로 전체 데이터의 만큼을 학습한 지역 모델 파라미터를 동기화해야 한다. Synchronous SGD는 모델 파라미터를 동기화하기 위해서 컴퓨팅 노드 간의 통신이 필요하지만, pipelined SGD는 동기화할 모든 지역 모델 파라미터가 동일한 컴퓨팅 노드에 존재하기 때문에 통신 비용이 없다는 장점이 있다. 반면, synchronous SGD는 모델 파라미터의 동기화 주기를 자유로이 조절할 수 있으나 pipelined SGD는 이라는 고정된 주기로만 동기화해야 하며 최대 에 해당하는 모델 사본을 저장할 메모리 공간을 필요로 하는 문제가 있다.
IV. 연산량 및 통신량 분석
본 장에서는 연산량 및 통신량 분석의 계산을 간단하게 하기 위하여 모든 층의 뉴런 개수가 같은 MultiLayer Perceptron(MLP) 모델을 가정한다.
4.1 연산량 분석
각 층이 개의 뉴런으로 구성된 층의 MLP에 대하여 크기의 mini-batch로 SGD의 forward pass 및 backward pass를 수행하기 위해서는 의 계산량을 필요로 한다.
개의 컴퓨팅 노드를 사용할 경우 synchronous SGD, asynchronous SGD, pipelined SGD 모두 각 컴퓨팅 노드는 한 epoch 동안 의 연산을 수행한다. 여기서 은 전체 mini-batch의 개수이다.
일반적인 asynchronous SGD에서 파라미터 서버는 마스터 모델을 갱신하기 위해서 한 epoch 동안 의 연산을 수행한다. Synchronous SGD에서는 번째 mini-batch마다 모델 파라미터 동기화를 수행할 경우 마스터 모델 갱신을 위한 계산량을 로 줄일 수 있다. Delayed gradient를 상관하지 않거나 근사적인 방법으로 영향을 줄이는 pipelined SGD[30,31,32,33,34,35]는 모델 파라미터 동기화를 수행하지 않기 때문에 마스터 모델 갱신을 위한 추가 연산을 필요로 하지 않는다. 지연된 시간만큼 모델 사본을 유지해서 delayed gradient 문제를 해결하는 pipelined SGD[37,38]는 모델 병렬화에 의해서 컴퓨팅 노드의 모델 크기가 로 줄지만 동기화해야 할 모델 파라미터 수가 모델 사본 수만큼 증가하기 때문에 결과적으로 모델 파라미터 동기화를 위해서 의 계산량을 필요로 한다.
4.2 통신량 분석
Asynchronous SGD에서는 모든 컴퓨팅 노드가 매 mini-batch마다 모델 동기화를 위해서 파라미터 서버와 gradient 또는 weight를 주고받기 때문에 한 epoch 동안 통신량은 이다. Synchronous SGD에서는 번째 mini-batch마다 모델 파라미터 동기화를 수행할 경우 통신량을 로 줄일 수 있다. Pipelined SGD에서는 컴퓨팅 노드 간에 forward pass 값이나 backward pass에서 역전파되는 오류 값을 전달하기 위해서 통신이 필요하다. 따라서, 인접한 컴퓨팅 노드 사이에 forward pass 및 backward pass 통신을 위한 전용 통신망이 각각 있는 경우 한 epoch 동안 통신량은 이 된다. 모델 동기화를 수행하는 pipelined SGD의 경우 동기화할 모델 파라미터가 모두 같은 컴퓨팅 노드에 있기 때문에 모델 동기화를 위한 추가적인 통신은 필요하지 않다. 각 병렬화 방법의 연산량과 통신비용은 Table 1에 정리되어 있다.
V. 결 론
본 논문에서는 DNN 학습을 위한 여러 가지 병렬 알고리즘에 대하여 알아보았다. DNN 기반의 알고리즘은 많은 데이터를 사용하여 대규모의 신경망을 구축할수록 인식 성능이 향상됨을 기대할 수 있다. 예를 들어 다수 화자의 목소리가 섞인 소리 신호에서 음성을 분리하고 인식하는 CHiME 챌린지에서도 상위권 알고리즘들의 신경망 규모는 계속하여 증가하는 추세이다.[39] 이러한 대규모의 신경망을 단일한 컴퓨팅 노드로 학습시키는 것은 한계가 있기 때문에 여러 컴퓨팅 노드에서 나누어 병렬로 학습하는 알고리즘이 필수적이다.
병렬 학습 알고리즘은 크게 학습 데이터를 분할해서 동시에 수행하는 데이터 병렬화 방식과 모델을 분할해서 동시에 수행하는 모델 병렬화 방식으로 나뉜다. 데이터 병렬화 방식은 모델 파라미터 동기화 방법에 따라서 synchronous SGD와 asynchronous SGD로 나뉜다. 모델 병렬화 방식은 모델 파라미터를 여러 컴퓨팅 노드로 분산해서 학습을 진행하는데, 특히 층 단위로 분산하는 pipelined SGD가 연산 자원을 효율적으로 사용하면서 통신량이 적은 것을 알 수 있었다. 데이터 병렬화 방식과 모델 병렬화 방식 모두 순차적 수행이 필요한 SGD 알고리즘을 병렬화하기 때문에 gradient 값을 근사적인 방법으로 구하는데, 이러한 근사 gradient의 영향을 최소화하는 여러 연구가 진행되어왔다.