I. 서 론
미세천공판(Micro-Perforated Plates, MPP)은 통상 구멍의 직경이 1 mm 이하인 미세한 구멍이 다수 뚫린 판을 말하는데 음파가 좁은 구멍을 통해 이동하면서 공기의 점탄성으로 인한 저항으로 음향파워가 손실되어 흡음효과가 발생하며 기본적으로 Helmholtz 공명기 원리와 같다.[1] MPP가 기존의 다공성 흡음재에 비해 가볍고, 친환경적이며 내구성이 뛰어나다는 장점 때문에 MPP 흡음재에 관한 많은 연구가 이루어졌다. 단일 MPP로 얻을 수 있는 흡음대역이 제한적이므로 이를 확장하는 다양한 수단이 연구되었는데 예를 들어 다중 MPP의 배열,[2,3] 두 가지 이상의 다른 MPP의 병렬배열,[4,5] 판이나 멤브레인과 결합하여 저주파수대역의 흡음 성능을 추가하는 방법[6,7] 등을 들 수 있다.
MPP의 음향투과에 관한 연구는 흡음연구에 비해 수가 매우 적다. Toyoda와 Takahashi,[1] Mu et al.,[8] Dupont et al.[9]은 무한 MPP 시스템의 음향투과손실(Sound Transmission Loss, STL)을 다루었는데 천공의 효과는 기존 이중 판의 STL에서 발생하는 질량-스프링-질량 공진의 골(dip)을 완화시킬 수 있음을 보였다. Kim et al.[10]은 무한 다중 MPP 구조에서 전달함수법을 이용하여 STL을 유도하는 공식을 제시하였으며 전 주파수 영역에서 미세천공의 영향을 검토하였다. Kim et al.[10]은 또한 미세천공의 임피던스로 인해 등가 복소수질량을 포함하는 변형된 질량법칙(mass-law)을 유도하였고 천공율이 커지면 STL은 감소함을 보였다. Bravo et al.[11,12]은 직사각형[11]및 원판 형상[12]의 MPP 구조물의 흡음과 차음성능을 해석적으로 다루었고 임피던스 튜브를 이용한 측정결과와 비교하였다.
본 논문은 직사각형 단면을 다룬 Reference [13]의 방법을 원형 단면을 갖는 임피던스 튜브내에 설치된 다중 탄성 MPP에 적용한 것으로 전달함수법을 이용하여 STL의 공식을 유도하였다. 임피던스 튜브내에서 시편의 지지는 강체지지(clamped)로 가정하는 것이 일반적인데 Reference [13]에서는 직사각형 판에 대한 엄밀해가 없으므로 근사식을 이용할 수 밖에 없었으며 이로 인한 오차가 발생한다. 그러나 원형 단면은 강체지지 모드를 정확하게 표현할 수 있는 장점이 있다. 본 연구결과는 시편의 흡음 및 차음 성능 평가에 널리 쓰이는 원통형 임피던스 튜브에 대해 측정결과를 비교할 수 있는 해석적 수단을 제공한다. 원형 단면을 다룬 기존 결과[12]와의 가장 큰 차이는 판의 진동으로 인한 음의 방사효과를 포함한 엄밀해를 유도한 점이다. 본 논문에서 제안하는 방법은 임의의 개수의 MPP에 대해서 적용이 가능하며 각각의 탄성 판은 미세천공이 없는 경우도 가능하다. 본 해석결과를 유한요소법을 사용한 수치해석결과와 비교하여 정확성을 검증하였다.
II. 음향투과해석
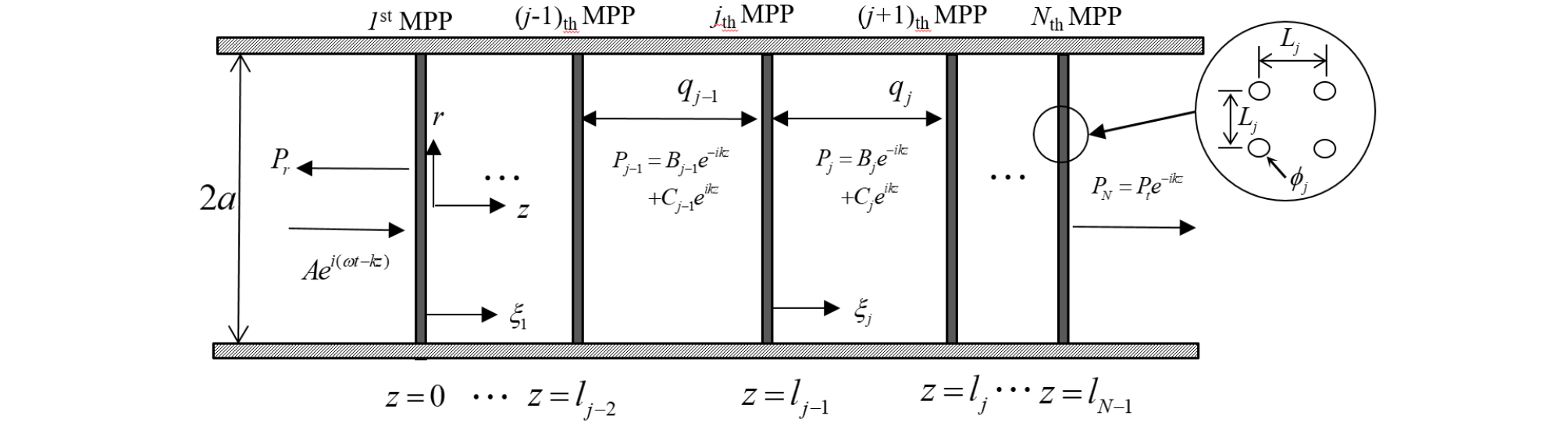
Fig. 1과 같이 반경이 인 원통형 임피던스 튜브 내에 설치된 다중 MPP에 음파가 입사하는 경우를 고려한다. j번째 MPP와 (j+1)번째 MPP의 간격은 이며 은 반경방향, 는 원주방향, z는 길이방향 좌표이다. 왼쪽에서 평면파 가 입사할 때 임피던스 튜브 내부에 발생하는 음장은 튜브가 강체라고 가정하면 표면 에서는 속도가 0이 되어야 한다. 본 연구에서는 임피던스 튜브내의 평면파만 고려하는데 직경이 100 mm인 원통에서 평면파 조건을 만족하는 주파수 한계는 [14](와 는 각각 주파수와 음속)에서 2010 Hz로 주어지지만 관심 주파수대역을 상용 임피던스 튜브의 평면파 권고치인 1600 Hz 이하로 한정한다. 첫 번째 판의 왼쪽에서는 다음과 같이 반사파가 발생하며
| $$p_r=P_re^{(i\omega t+kz)},$$ | (1) |
()번째 캐비티()에 발생하는 압력 은 다음과 같이 주어진다.
| $$p_{j-1}=B_{j-1}e^{i(\omega t-kz)}+C_{j-1}e^{i(\omega t+kz)},$$ | (2) |
여기서 는 각속도, 파수, , 은 미지수 계수이다. 같은 방법으로 번째 캐비티()에 발생하는 압력 는 다음과 같이 주어진다.
| $$p_j=B_je^{i(\omega t-kz)}+C_je^{i(\omega t+kz)}.$$ | (3) |
마지막 번째 MPP를 통과하는 파는 다음과 같이 주어진다.
| $$p_N=P_te^{i(\omega t-kz)}.$$ | (4) |
번째 MPP의 경계조건은 판의 평균 속도를 이용하여 다음과 같이 주어진다.
| $$-\frac1{i\omega\rho}\frac{\partial p}{\partial z}={\overline v}_j\;\mathrm{at}\;z=l_{j-1},$$ | (5) |
여기서 는 공기의 밀도, 는 번째 MPP의 평균속도이다. 판의 속도를 , 구멍 안에서의 평균 공기속도를 라고 하면 다음 관계가 성립한다.[15]
| $${\overline v}_j=v_{j,p}(1-\sigma_j)+v_{j,f}\sigma_j=v_{j,p}+(v_{j,f}-v_{j,p})\sigma_j,$$ | (6) |
여기서 는 천공율로 구멍의 직경을 , 구멍 중심 간의 거리를 이라고 하면 로 정의된다.
판의 진동과 임피던스와의 관계는 다음과 같이 주어진다.[15]
| $$Z_{j,resist}(v_{j,f}-v_{j,p})+Z_{j,react}v_{j,f}=p_{j-1}-p_j,$$ | (7) |
여기서 구멍의 임피던스 는 판의 평균 임피던스를 라고 하면 로 주어진다. Eqs. (1)과 (2)로부터 압력차이는 다음과 같이 주어진다.
| $$\Delta p_j=B_{j-1}e_{}^{-ikl_{j-1}}+C_{j-1}e_{}^{ikl_{j-1}}-B_je_{}^{-ikl_{j-1}}-C_je_{}^{ikl_{j-1}}.$$ | (8) |
구멍의 직경이 매우 작은 경우 임피던스 는 다음과 같이 주어진다.[2]
여기서 . Eq. (9)에서 는 판의 두께, 는 공기의 점도(viscosity)로 로 주어진다. 위의 식에서 주의해야 할 점은 시간에 대한 항을 로 가정하면 의 허수부분은 가 되며 로 가정하면 의 허수부분은 가 되어야 한다.
Eqs. (6)과 (7)로부터 다음 관계가 성립한다.
| $$\overline{v_j}=\gamma_jv_{j,p}+\frac{\Delta p_j}{Z_{0,j}}=\gamma_jv_{j,p}+\frac{\sigma_j\Delta p_j}{Z_j},$$ | (10) |
여기서 . Eqs. (2), (3), (5)로부터 미지수 사이에 다음과 같은 관계가 주어진다.
| $$-B_{j-1}e^{-ikl_{j-1}}+C_{j-1}e^{ikl_{j-1}}=-B_je^{-ikl_{j-1}}+C_je^{ikl_{j-1}}\;\mathrm{at}\;z=l_{j-1}.$$ | (11) |
판의 진동변위를 라고 하면 판의 속도는 로 주어지고 평판의 변위에 대한 지배방정식은 다음과 같이 된다.
| $$D_j\nabla^4{\widetilde\xi}_j-M_j\omega^2{\widetilde\xi}_j=\Delta p_j.$$ | (12) |
단, 여기서 는 j번째 판의 탄성계수, Poisson 비, 밀도이며 은 판의 표면밀도를 나타낸다. 탄성 MPP의 천공율이 크다면 Eq. (12)의 적용은 오류를 초래하지만 대부분의 MPP는 천공율이 매우 작은 경우에 사용하며 본 논문에서 다루는 예제는 천공율이 최대 0.2 %이므로 Eq. (12)의 적용에는 문제가 없다. Eq. (12)판의 댐핑은 Eq. (12)에서 복소수 탄성계수 를 사용하여 고려하였는데 손실계수 는 0.01을 가정하였다.
단순지지 또는 클램프 지지된 원판의 축대칭 진동 모드는 다음과 같다.[16]
| $${\overline\xi}_j=\sum_{m=1}^\infty a_{jm}\psi_m(r),$$ | (13) |
여기서 은 Bessel 함수 와 의 조합으로 이루어지는데 에서 경계조건 을 만족하도록 다음과 같이 주어진다.
| $$\psi_m(r)=I_0(\frac{\lambda_mr}a)-\frac{I_0(\lambda_m)}{J_0(\lambda_m)}J_0(\frac{\lambda_mr}a).$$ | (14) |
변수 은 경계조건에 따라 다음 식을 만족한다.
1) 단순지지:
| $$\frac{I_1(\lambda_m)}{I_0(\lambda_m)}+\frac{J_1(\lambda_m)}{J_0(\lambda_m)}=\frac{2\lambda_m}{(1-\nu_j)},$$ | (15) |
2) 클램프지지:
| $$\frac{I_1(\lambda_m)}{I_0(\lambda_m)}+\frac{J_1(\lambda_m)}{J_0(\lambda_m)}=0.$$ | (16) |
Eqs. (15)와 (16)을 만족하는 처음 6개의 의 값은 Reference [17]에 제시되었다. Poisson 비 는 단순지지의 경우에만 영향을 주고 클램프 지지에는 영향이 없다. 판의 고유진동수는 다음과 같이 주어진다.
| $$\omega_{jm}=\frac{\lambda_m^2}{a^2}\sqrt{\frac{D_j}{\rho_{j,p}h_j}}.$$ | (17) |
Eq. (12)의 좌변 항은 다음과 같이 고유진동수와 고유모드의 형태로 표현할 수 있다.
| $$D_j\nabla^4{\widetilde\xi}_j-M_j\omega^2{\widetilde\xi}_j=\sum_{m=1}^\infty a_{jm}M_j(\omega_{jm}^2-\omega^2)\psi_m(r).$$ | (18) |
Eq. (18)을 이용하여 Eq. (12)의 양 변에 를 곱하고 단면에 대해 적분한 후 모드의 직교성을 이용하면 다음과 같은 식이 얻어진다.
| $$M_jT_m(\omega_{jm}^2-\omega^2)a_{jm}=\lbrack B_{j-1}e_{}^{-ikl_{j-1}}+C_{j-1}e_{}^{ikl_{j-1}}-B_je_{}^{-ikl_{j-1}}-C_je_{}^{ikl_{j-1}}\rbrack\Gamma_m,$$ | (19) |
여기서
| $$T_m=\frac1{\pi a^2}\int_0^{2\pi}\int_0^a\psi_m^2(r)\;r\;dr\;d\theta=\frac2{a^2}\int_0^a\psi_m^2(r)rdr,$$ | (20) |
| $$\Gamma_m=\frac2{a^2}\int_0^a\psi_m(r)rdr.$$ | (21) |
Eqs. (20)과 (21)에서 적분 값 과 은 에 무관함을 알 수 있다. Eq. (2)의 을 Eq. (5)에 대입하여 얻은 와 Eq. (13)의 를 Eq. (10)에 대입하고 단면에 대해 적분하면 다음 식을 얻는다.
| $$\frac1{\rho c}(B_{j-1}e^{-ikl_{j-1}}-C_{j-1}e^{ikl_{j-1}})=i\omega\gamma_j\sum_{m=1}^\infty a_{jm}\Gamma_m+\frac{\sigma_j}{Z_j}\Delta p_j.$$ | (22) |
Eq. (8)의 를 Eq. (22)에 대입후 Eq. (19)에서 을 소거하여 정리하면 다음과 같이 된다.
| $$B_{j-1}e_{}^{-ikl_{j-1}}(1-K_j)-C_{j-1}e_{}^{ikl_{j-1}}(1+K_j)=-K_j(B_je_{}^{-ikl_{j-1}}+C_je_{}^{ikl_{j-1}}).$$ | (23) |
단,
| $$K_j=\gamma_j\beta_j+\rho c\sigma_j/Z_j, $$ | (24) |
| $$\beta_j=\sum_{m=1}^\infty\frac{i\rho c\omega}{M_j(\omega_{jm}^2-\omega^2)}\left(\frac{\Gamma_m^2}{T_m}\right).$$ | (25) |
Reference [17]에 을 수치적분을 수행하여 계산한 결과를 나타냈다. Eqs. (11)과 (23)을 다음과 같이 매트릭스 형태로 표현할 수 있다.
| $${\mathbf X}_{\mathrm j-1}={\mathbf H}_{\mathrm j}{\mathbf X}_{\mathrm j}.$$ | (26) |
단
| $${\mathbf H}_j=\frac1{2K_j}\begin{bmatrix}2K_j+1&-e^{2kl_{j-1}}\\e^{-2kl_{j-1}}&2K_j-1\end{bmatrix},$$ | (27) |
| $$\mathbf X_j^T=({\mathbf B}_{\mathit j\mathit,}{\mathbf C}_{\mathit j}).$$ | (28) |
첫 번째 MPP()와 마지막 MPP()에서 각각 로 정의되며 Eq. (26)을 순차적으로 적용하여 다음과 같이 단순화된 매트릭스 식으로 표현할 수 있다.
| $$\begin{bmatrix}A\\P_r\end{bmatrix}=\begin{bmatrix}G_{11}&G_{12}\\G_{21}&G_{22}\end{bmatrix}\begin{bmatrix}P_t\\0\end{bmatrix}.$$ | (29) |
Eq. (29)에서 반사파와 투과파는 각각 다음과 같이 주어진다.
| $$P_t/A=1/G_{11},$$ | (30) |
| $$P_r/A=G_{21}/G_{11}.$$ | (31) |
투과율과 STL은 각각 다음과 같이 주어진다.
| $$\tau=\vert P_t/A\vert^2,$$ | (32) |
| $$\mathrm{STL}=10\log(1/\tau).$$ | (33) |
III. 수치해석 예제
수치해석 예제로 지름 100 mm인 원판 MPP가 설치된 경우를 고려하였는데 경계조건은 클램프(clamp) 지지를 가정하였다. 시편의 재질은 강판으로 탄성계수, 밀도, Poisson 비는 각각 N/m2, 7800 kg/m3, 0.31이며 댐핑 값은 0.01을 가정하였다.
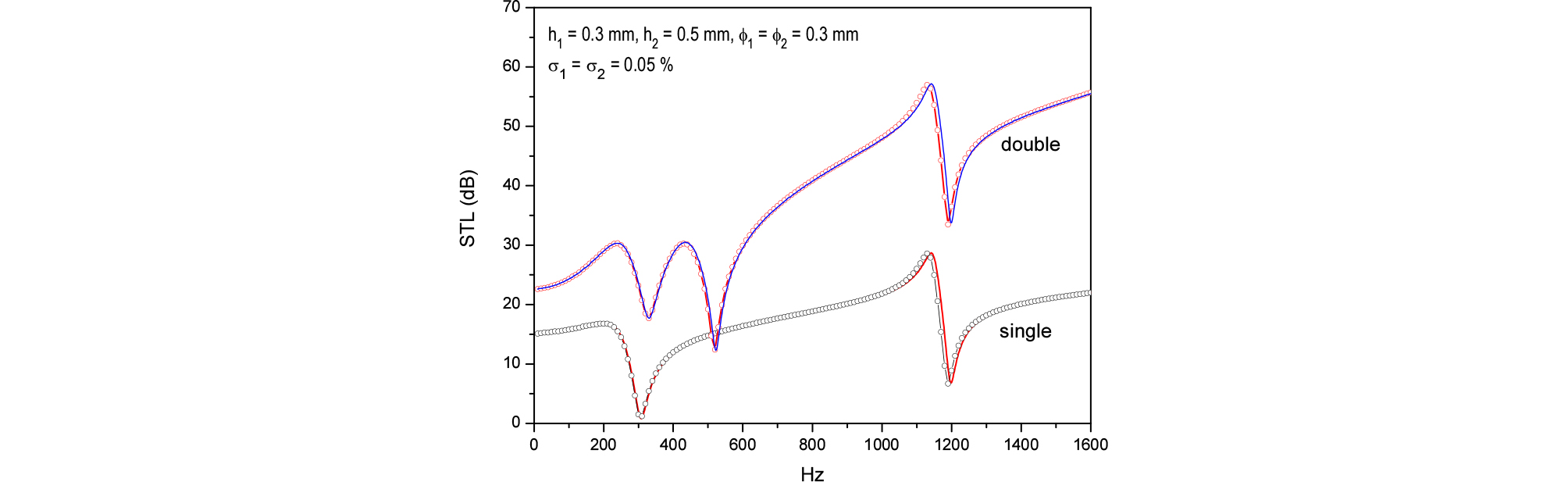
Fig. 2에는 단일 MPP와 이중 MPP에 대해 STL을 Eq. (33)을 사용한 예측(실선)과 Comsol[18]을 이용한 유한요소법(Finite Element Method, FEM) 해석결과(심볼)와 비교하였는데 구별이 잘 되지 않을 정도로 잘 일치함을 알 수 있다. Comsol에서는 천공의 임피던스를 Eq. (9)로 정의하고 댐핑은 Eq. (12)의 복소수 탄성계수로 입력할 수 있는 장점이 있다. Eq. (13)에서 모드 수는 10개로 한정하였고 1600 Hz 내에서는 충분히 수렴함을 확인하였다. Fig. 2에서 단일 MPP는 두께 0.3 mm, 이중 MPP는 두께가 각각 0.3 mm, 0.5 mm이고 공기층 간격은 50 mm이며 모든 MPP 구멍의 직경은 0.3 mm, 천공율은 0.05 %이다. 본 연구의 관심 주파수대역인 1600 Hz 보다 작은 공진주파수를 계산해보면, 두께 0.3 mm, 지름 100 mm의 원판의 공진주파수는 307 Hz, 1197 Hz, 두께 0.5 mm의 원판의 공진주파수는 512 Hz이며 Fig. 2에서 STL은 공진주파수에서 골을 보이는 것을 알 수 있다.
단일 MPP의 투과율과 STL은 Eqs. (32)와 (33)에서 각각 다음과 같이 주어진다.
| $$\tau=\vert\frac1{1+1/(2K_1)}\vert^2,$$ | (34) |
| $$\mathrm{STL}=10\log\;\left|1+\frac1{2\gamma_1\beta_1(1+\rho c\sigma_1/Z_1\gamma_1\beta_1)}\right|^{{}^2}.$$ | (35) |
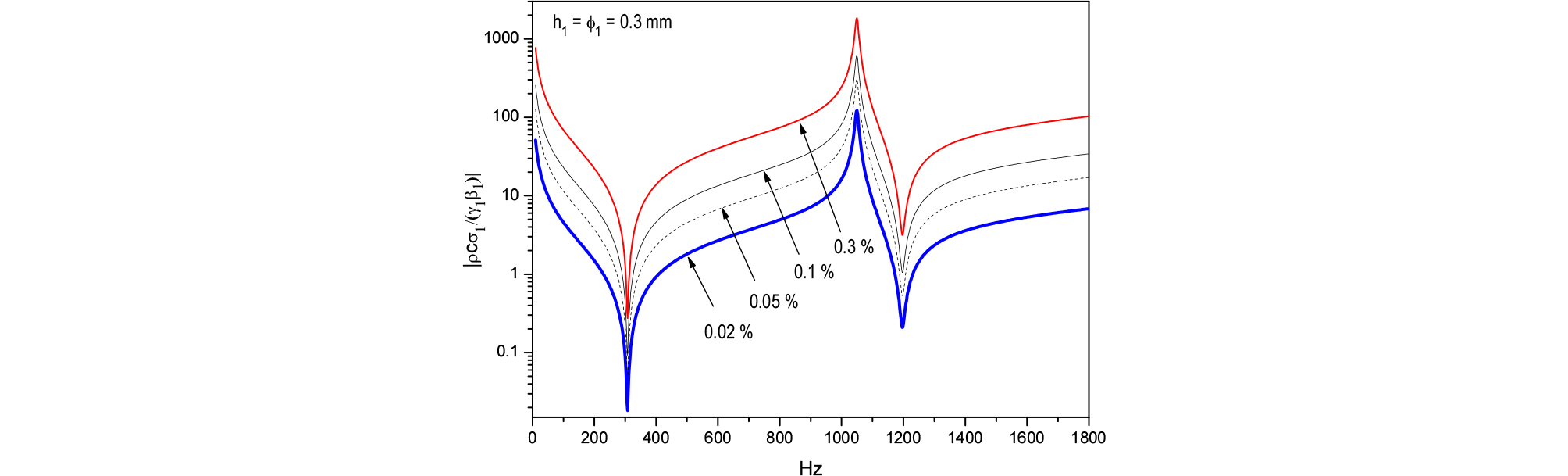
Fig. 3에는 Eq. (35)의 을 을 변화시켜 가며 나타냈는데 판의 고유진동수에서 골을 보이며 이 증가할수록 도 고유진동수를 제외하고는 증가하며 이는 MPP의 진동보다는 천공율의 영향이 더 크다는 것을 나타낸다.
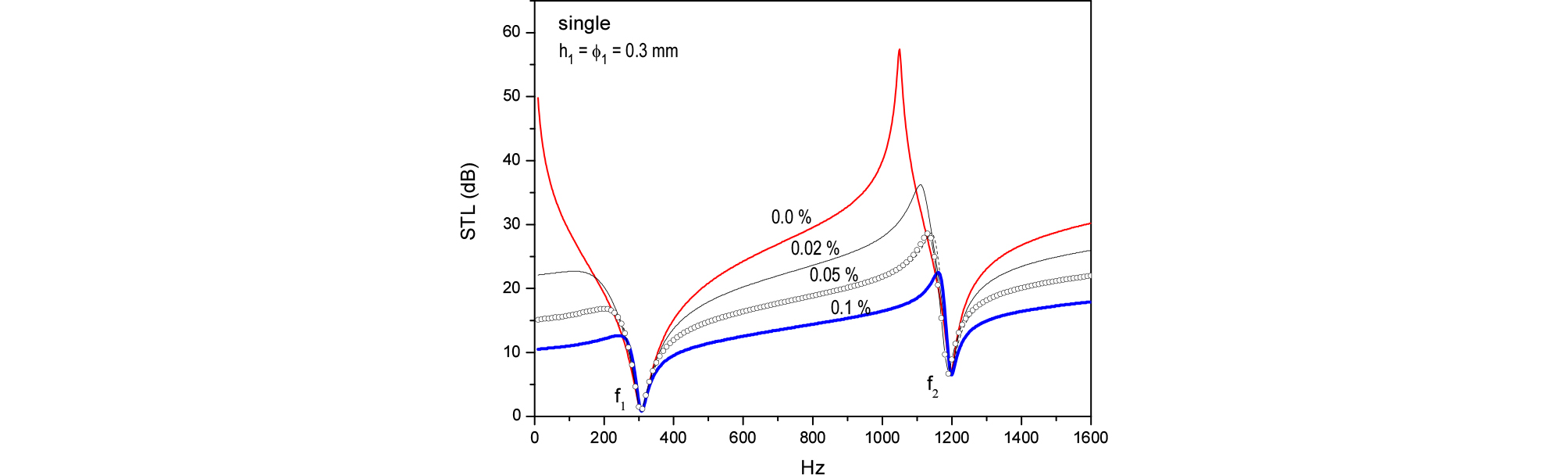
Fig. 4에는 Eq. (35)의 STL을 나타냈는데 Fig. 3에서 알수 있듯이 이 커질수록 STL은 감소한다. Eq. (25)에서 인 경우 STL은 골을 보이며 이는 MPP의 고유진동수에 해당된다. 반면, STL의 피크는 를 만족하는 주파수 에서 발생한다.[19]
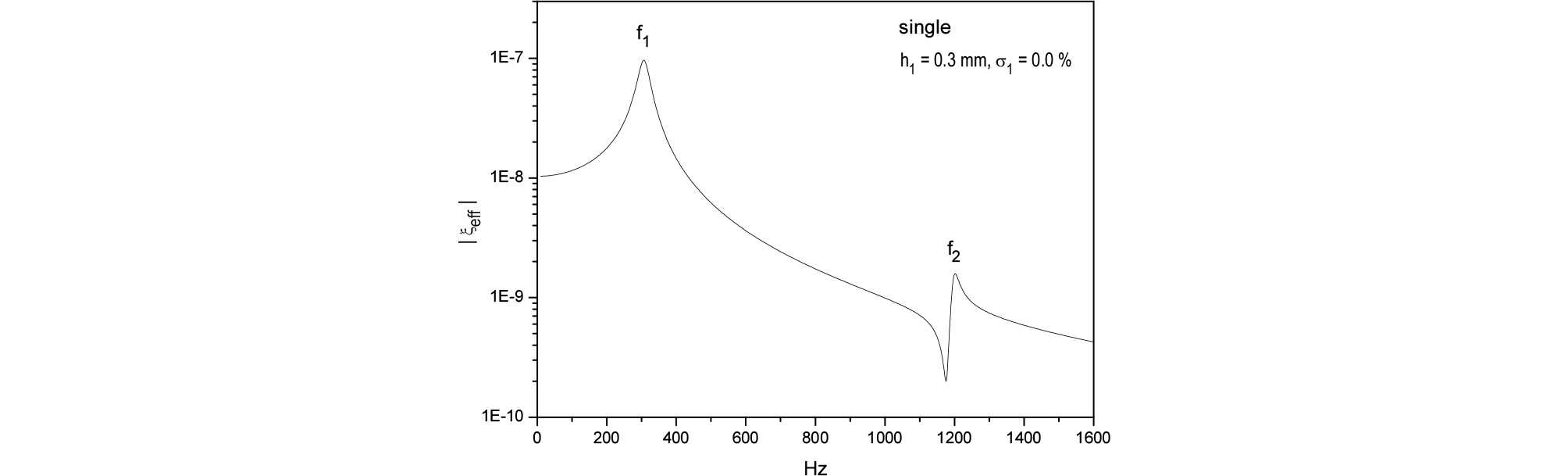
천공이 없는 단일 판의 변위를 단면에 대해 평균한 는 다음과 같이 주어진다.
| $$\xi_{eff}=\frac2{a^2}\int_0^a\overline\xi rdr=\sum_{m=1}^\infty\frac4{\lambda_m}\frac{I_1(\lambda_m)}{(2K_1+1)M_1T_m(\omega_m^2-\omega^2)}.$$ | (36) |
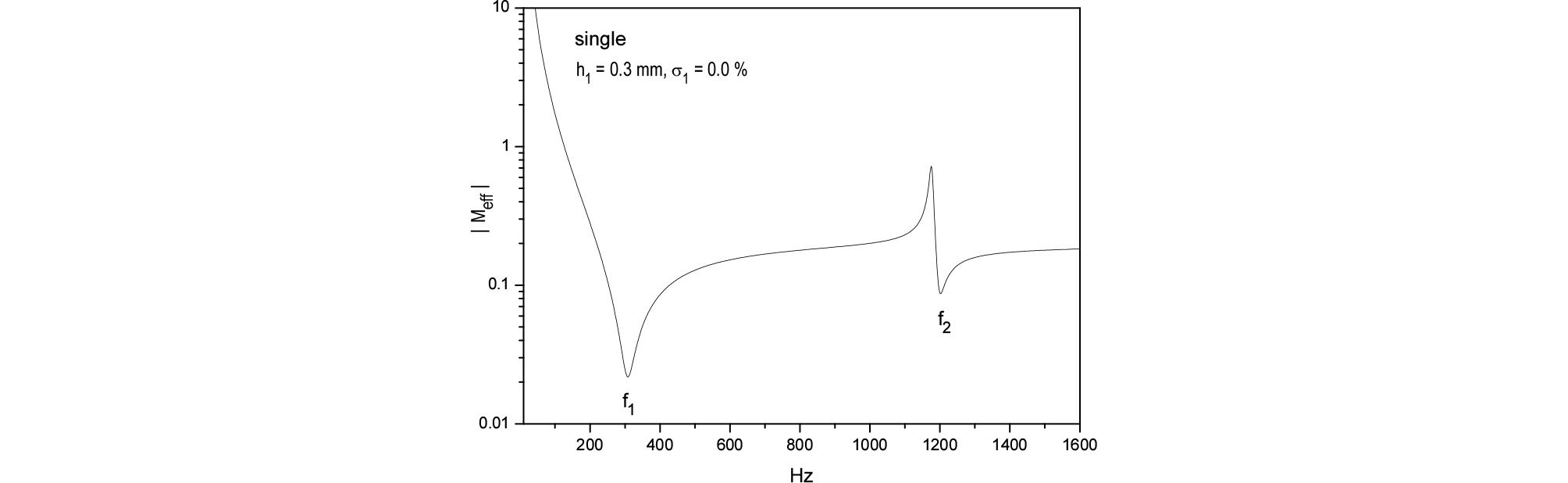
유효 질량 는 Eq. (36)의 평균 변위를 이용하여 단일 판이 독립적으로 운동한다는 가정으로부터 다음과 같이 주어진다.
| $$F\cdot\pi a^2=-\omega^2M_{eff}\xi_{eff}.$$ | (37) |
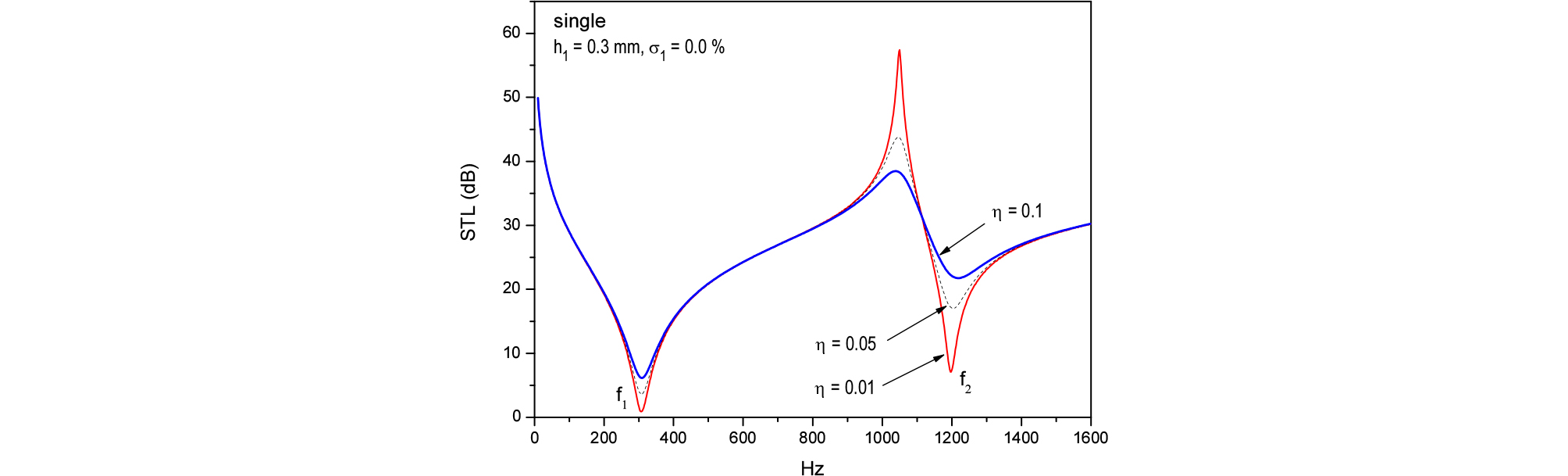
Figs. 5와 6에는 Eqs. (36)과 (37)의 평균 변위와 유효 질량을 나타냈는데() 고유진동수에서 평균 변위는 피크를 보이나, 반대로 판의 유효 질량은 낮은 값을 보이는데 이는 STL의 낮은 값을 설명한다. Fig. 7에는 댐핑을 증가시키면서 단일 판의 STL을 보였는데 댐핑이 증가할수록 피크와 골이 둔화됨을 보여준다. 따라서 판의 댐핑을 증가시키는 것이 STL의 저하를 막는 중요한 수단임을 알 수 있다.
공기층 간격이 인 이중 MPP의 투과율은 다음과 같이 주어진다.
| $$1/\tau=\left|(1+\frac1{2K_1})(1+\frac1{2K_2})-\frac{e_{}^{-2ikq_1}}{4K_1K_2}\right|^{{}^2}.$$ | (38) |
만일 이라면 STL은 다음과 같이 된다
| $$\mathrm{STL}=10\log\left|1+\frac1{2K_1}+\frac1{2K_2}+\frac{ikq_1}{2K_1K_2}\right|^{{}^2}.$$ | (39) |
Eq. (39)에서 STL의 골은 MPP의 고유진동수 외에 다음 조건을 만족할 때 나타난다.
| $$K_1+K_2+ikq_1=0.$$ | (40) |
이는 두 MPP와 중간의 공기층이 발생하는 질량-스프링-질량 진동에 해당하는 공진주파수를 의미한다. 만일 두 개의 판이 동일하고 의 경우 판의 처음 모드만 고려하여 Eq. (40)의 해는 다음과 같이 주어진다.[19]
| $$\omega_r^2=\frac1q\frac{2\rho c^2\Gamma_1^4}{M_1T_1^2}+\omega_1^2.$$ | (41) |
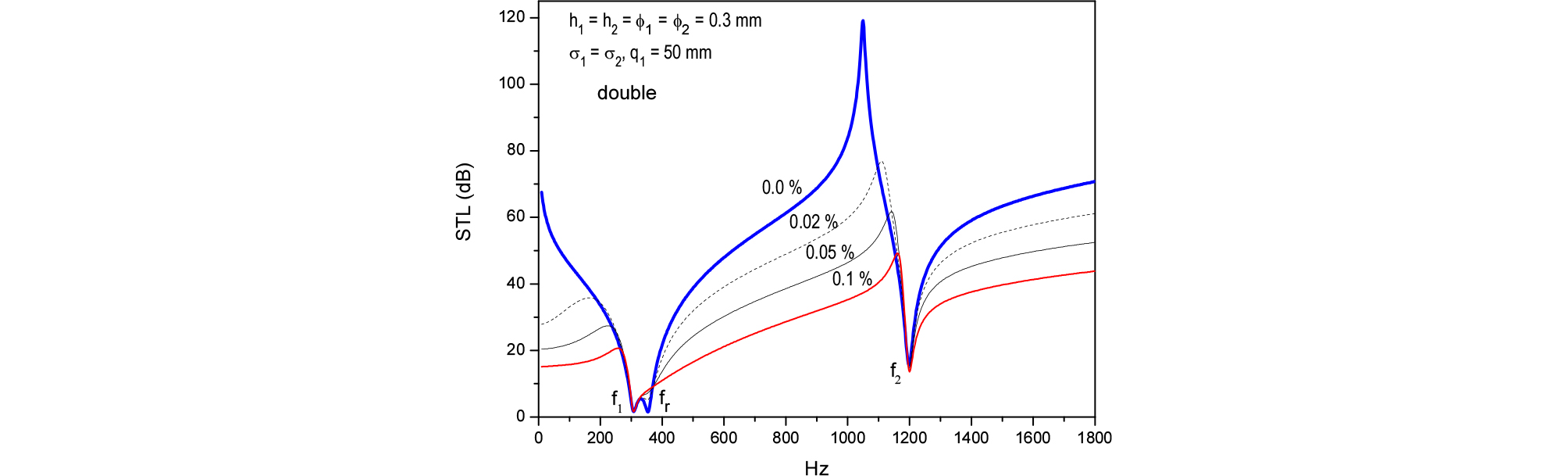
Fig. 8에는 이중 MPP의 두께와 구멍의 직경이 각각 0.3 mm, 0.3 mm, 50 mm일 때 STL을 나타냈는데 두 MPP의 천공율은 같으며 0.0 %, 0.02 %, 0.05 %, 0.1 %이다. 천공율이 커질수록 단일 MPP와 마찬가지로 STL은 감소함을 알 수 있다. Fig. 8에서 천공율이 제로인 경우 Eq. (41)에 의한 공진주파수는 = 356 Hz이다. 반면, Eq. (39)에 근거한 STL 값에서 확인되는 공진주파수는 354 Hz이며 따라서 Eq. (41)은 의 경우 충분히 정확한 근사식임을 알 수 있다.
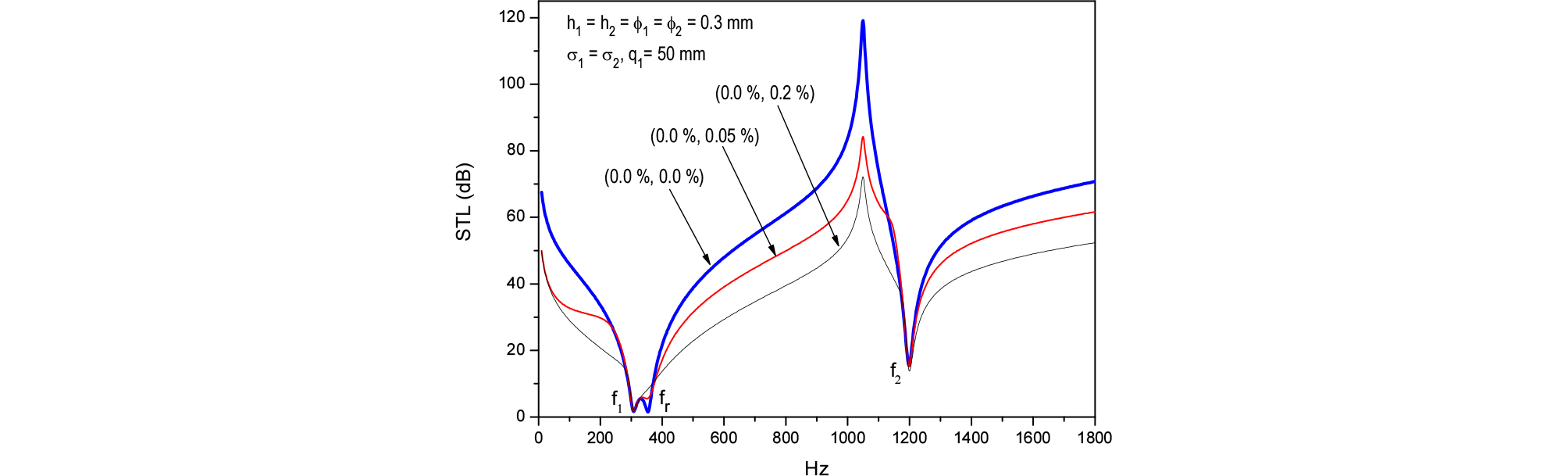
Fig. 9에는 두 MPP의 천공율이 각각 (0.0 %, 0.0 %), (0.0 %, 0.05 %), (0.0 %, 0.2 %)로 변할 때 STL을 나타냈는데 MPP의 두께 및 구멍의 직경은 Fig. 8과 같다. 역시 Fig. 9에서도 천공율이 커질수록 STL은 감소함을 보여준다.
IV. 결 론
본 연구에서는 원통형 임피던스 튜브내에 설치된 다중 탄성 MPP의 STL을 평면파 가정 하에서 예측하는 공식을 제안하였는데 FEM 결과와 잘 일치함을 알 수 있다. 천공율이 증가할수록 STL은 판의 진동보다는 미세천공율에 좌우되며 STL은 감소한다. STL은 판의 공진주파수에서 골을 보이는데 특히 이중 MPP의 STL은 질량-스프링-질량 진동에 해당하는 공진주파수에서 골을 보인다. 본 연구에서 제안한 STL 예측 모델은 임의의 다중 MPP에 적용이 가능하며 각각의 판은 미세천공을 포함하거나 하지 않는 두 가지 경우 모두 가능하다.