I. 서 론

제한된 환경에서도 해양 탐사가 가능한 무임잠수정(Autonomous Underwater Vehicles, AUV)의 활용도가 높아지고 운용 거리가 멀어지면서, 장거리 심해 환경에서의 수중음향통신 연구의 필요성이 높아지고 있다. 국외에서는 이미 활발하게 진행되고 있으며^{[1], [2], [3], [4]}, 특히 미국의 Scripps 해양 연구소와 일본의 Japan Agency for Marine-Earth Science and Technology (JAMSTEC)과 같은 기관에서 다수의 해상실험과 함께 집중적으로 연구를 수행하고 있으며,^{[5], [6], [7], [8], [9], [10], [11], [12], [13], [14], [15], [16]} 최근 국내에서도 관련 연구를 수행하였다.^{[17], [18], [19]}

장거리 심해 환경에서의 수중음향통신은 긴 전달 거리로 전달손실이 크고, 시간 지연 확산이 커지므로 인접 심볼 간 간섭으로 인해 통신 성능이 저하된다. 이러한 문제를 해결하기 위해 대부분의 연구는 다중 경로의 특성을 활용하는 수동형 시역전 처리 기반으로 수행되고 있으며,^{[5], [6], [7], [8], [10], [13], [15]} 수동형 시역전 처리에 다이버시티를 활용한다면 통신 성능을 더욱 향상시킬 수 있다. 다이버시티 결합 기법은 크게 4가지로 분류할 수 있으며, (1) 다수의 수신기로부터 측정한 신호를 이용하는 공간 다이버시티 결합, (2) 제한된 공간(한 개의 수신기) 및 다수의 시간대에서 수신된 신호를 이용하는 시간 다이버시티 결합,^{[6], [7], [19]} (3) 다양한 주파수와 주파수의 직교성을 이용하는 주파수 다이버시티,^[4] 그리고 (4) 음파의 전달 각도들을 통한 빔 형성을 이용하는 빔 다이버시티^{[9], [12], [14], [16]} 등으로 구분된다.

본 논문에서는 빔 다이버시티 결합 기법을 이용한 수동형 시역전 처리의 통신 성능 분석을 수행하고자 하며, 특히, 빔 다이버시티 결합 시에 다이버시티 개수 및 조합에 따른 통신 성능 결과를 비교하였다. 수직 선 배열 센서를 이용할 경우 기존 연구에서 이용한 수평 선 배열 센서보다 많은 수의 각도를 추정할 수 있으며,^{[9], [12]} 이를 통해 조합에 따른 성능 변화를 확인할 수 있다. 기존의 빔 다이버시티의 논문들은 대부분 빔 형성만(빔 다이버시티 = 1)을 다루고 있다. 데이터 분석을 위해 2018년 10월 포항 동방 해역에서 수행한 장거리 심해 수중음향통신 실험 데이터를 활용하였다.^{[18], [19]}

본 논문의 구성은 다음과 같다. II장에서는 빔 다이버시티 결합 기법을 이용한 수동형 시역전 처리 알고리즘에 관해서 설명하기로 한다. III장에서는 본 논문에서 활용한 실험 데이터 구성 및 환경과 송신 신호를 소개하고, IV장에서는 실제 해상실험 데이터를 활용하여 빔 다이버시티 기반의 수동형 시역전 처리를 통한 통신 성능 분석 결과를 보여준다. 마지막으로 V장에서는 본 논문의 결론을 맺는다.

II. 빔 다이버시티

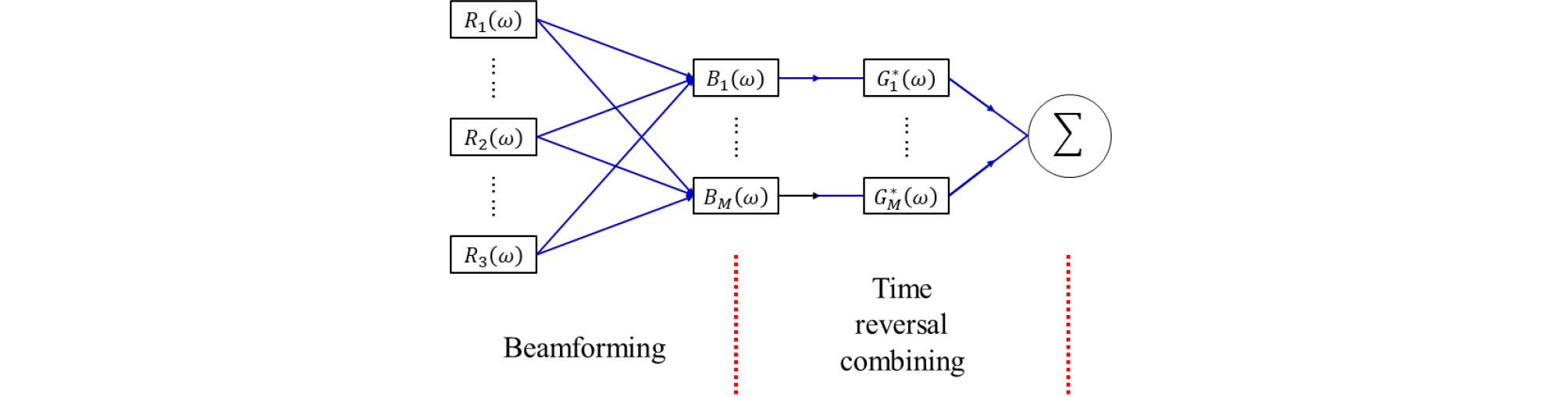
빔 형성 기법은 배열 센서로 수신되는 신호의 위상차를 이용하는 기법으로써, 배열 센서에 신호가 들어오는 방향을 추정할 수 있는 기법이다. Fig. 1은 시간 영역에서의 빔 형성을 보여주는 모식도이다. Fig. 1의 중앙에 나타낸 것과 같이 수신 신호들을 신호가 들어오는 방향으로 빔 조향한다면, 해당 방향으로 들어오는 신호는 동일한 위상으로 정렬될 것이다. 또한, 동시에 다른 각도를 통해 들어오는 신호들의 위상차는 더욱 커질 것이다. 이를 모든 수신기에 대하여 더하면 다중 경로의 영향을 완화할 수 있다.

Fig. 1.

Diagram of the beamforming in time domain.

수중에서 도파관(waveguide)을 통해 전달된 신호는 다중 경로에 의해 왜곡된 형태로 수신되지만, 이러한 다중 경로의 존재는 곧 여러 개의 각도 정보가 존재함을 나타내는 것이기도 하다. 빔 다이버시티 결합 기법은 이러한 여러 개의 각도로의 빔 조향을 통해 획득한 신호들을 결합하는 기법을 나타낸다. 즉, 빔 조향된 신호들은 빔 조향 각도의 개수만큼의 수신기에 수신된 신호로써 생각할 수 있다. Fig. 2는 빔 다이버시티 결합 기법을 이용한 수동형 시역전 처리의 나타내는 블록 다이어그램이다. Fig. 2는 빔 형성 과정과 시역전 처리 과정, 두 가지로 과정으로 구분된다.

Fig. 2.

Block diagram of passive time reversal processing with beam diversity.

식 전개의 편의를 위해 주파수 영역으로 식을 표현하기로 하며, Fig. 2에서 $R\left(\omega \right)$와 $B\left(\omega \right)$는 각각 수신기를 통해 수신된 신호와 빔 조향된 신호의 푸리에 변환 식을 나타낸다. $B\left(\omega \right)$는 Eqs. (1)과 (2)를 통해 계산할 수 있으며, Eq. (2)에서 $W\left(\omega \right)$는 빔 조향을 위한 가중치 벡터를 의미한다.

여기서 $N$과 $M$은 각각 수신기의 개수와 빔 개수를 의미한다. 또한, $t_{dn}^m$와 윗 첨자 $H$는 각각 $m$번째의 방향으로 $n$번째 채널에 반영되는 시지연과 에르미트 전치를 나타낸다.

빔 조향을 통해 얻은 신호들을 새로운 수신 신호로써 간주하여 수동형 시역전 처리를 수행하는 것을 빔 다이버시티 결합 기법 기반의 수동형 시역전 처리로 정의할 수 있으며, Eqs. (3)과 (4)와 같은 수식을 통해 계산할 수 있다.

여기서 $G\left(\omega \right)$는 빔 조향된 신호의 전달 함수를 나타낸다.

Eqs. (1)과 (2)를 통해 계산한 빔 조향 과정은 Fig. 2에서 “beamforming”으로 표기한 영역과 대응되며, Eqs. (3)과 (4)를 통해 계산한 수동형 시역전 처리 과정은 Fig. 2에서 “time reversal combining”으로 표기한 영역과 대응된다.

III. 해상실험 환경

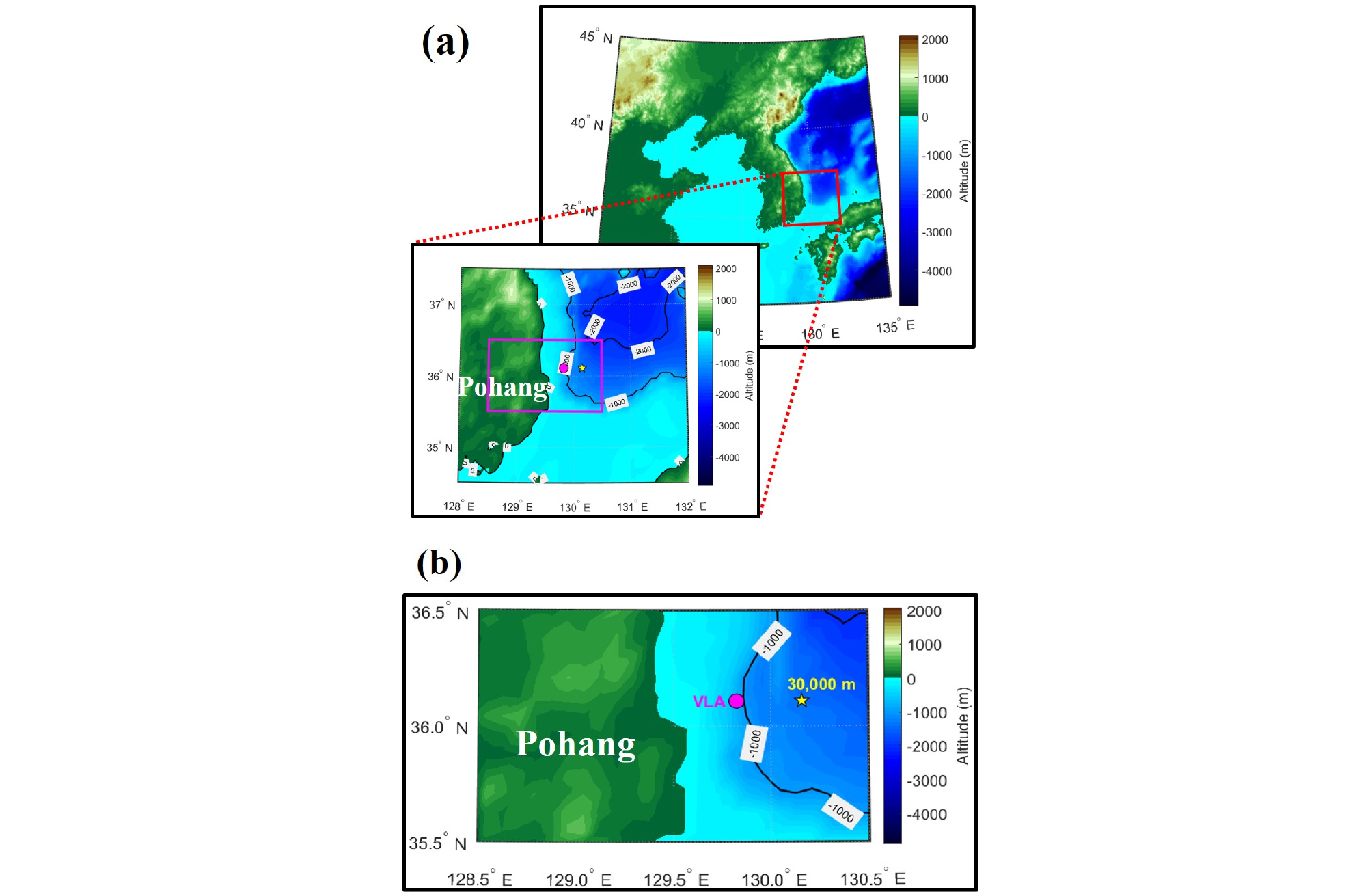
Biomimetic Long range Acoustic Communications 2018 (BLAC18)은 2018년 10월 포항 동방 해역에서 장거리 수중음향통신 통신 성능 분석을 위해 수행된 수중음향통신 실험이다. Fig. 3은 해상실험을 수행한 해역을 나타낸다. Fig. 3에서 수직 선 배열 센서가 설치된 장소를 Vertical Line Array(VLA)로 표기하였으며, 포항에서 50 km 떨어진 지점이다. 음원의 위치는 30 km로 표기하였으며, 수치는 음원과 수직 선 배열 센서 사이의 거리를 의미한다.

Fig. 3.

Experimental site.

Fig. 4는 실험 구성 및 실험 해역의 음속 구조를 나타낸다. 음원과 수신기 사이의 거리는 앞서 언급한 바와 같이 30 km이며, 데이터는 수직 선 배열 센서를 통해 수신하였다. 수직 선 배열 센서는 설계 주파수가 268 Hz인 2.8 m 등간격으로 총 16개의 센서로 구성되어 있으며, 해상실험 동안 수직 선 배열 센서 중심의 깊이는 200 m에 위치하였다. 음원 역시 200 m 깊이에 위치하였다.

Fig. 4.

Schematic of BLAC18 experiment.

실험 해역은 수심이 최대 1,700 m인 심해 환경이며, Conductivity, Temperature, Depth(CTD)를 이용하여 측정한 깊이별 음속 구조로부터 약 250 m에 음향 축이 위치함을 확인하였다.

해상실험 동안의 전송 신호는 채널 응답 특성 추정을 위해 Chirp 신호로 설계된 탐심 신호와 통신용 데이터로 구성된다. 통신용 데이터에는 심볼의 동기를 찾기 위해 255개의 심볼을 가진 M-sequence 신호가 포함되었다. 신호의 구성은 Fig. 5와 같으며, 탐심 신호와 통신용 데이터의 주파수 대역은 2.56 kHz의 중심 주파수와 640 Hz의 밴드 폭으로 설계되었다. 통신용 데이터는 512 bps의 전송률로 Binary Phase Shift Key(BPSK) 변조 방식을 사용하였으며, 인접 심볼 간 간섭을 줄이기 위해 roll-off factor가 0.25인 Root Raised Cosine(RRC) 필터를 변조와 복조 과정에서 정합 필터로 사용하였다. 데이터의 심볼 개수는 1,000개이다. 탐침 신호와 통신용 데이터의 길이는 각각 3 s와 2.45 s이다. 그리고 탐침 신호와 통신용 데이터 사이에 2 s의 무음 구간을 포함하였다.

Fig. 5.

Configuration of the transmitted signal packet.

IV. 해상실험 결과

4.1 음파 전달 각도 추정

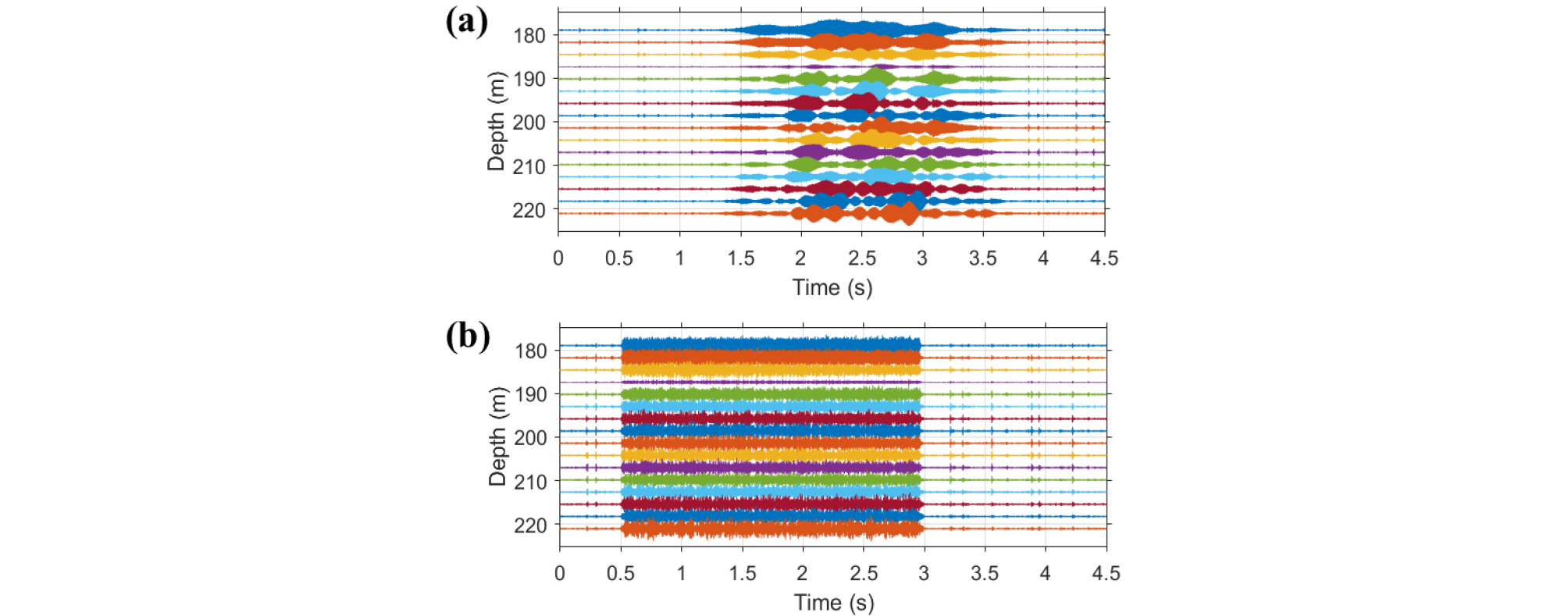
본 절에서는 해상실험 데이터로부터 음파의 전달 각도를 추정하고자 한다. 우선 음파의 전달 각도를 추정하는 기본적인 알고리즘인 재래식 빔 형성기법을 이용하여 추정한다. Fig. 6은 음원과 수신기 사이의 거리가 30 km일 때의 수신 신호를 나타낸다. Fig. 6(a)와 (b)는 각각 탐침 신호와 통신용 데이터를 나타낸다. 그림에서 가로축은 시간을, 세로축은 깊이를 의미한다.

Fig. 6.

Received signals; (a) Probe signal, (b) Data frame.

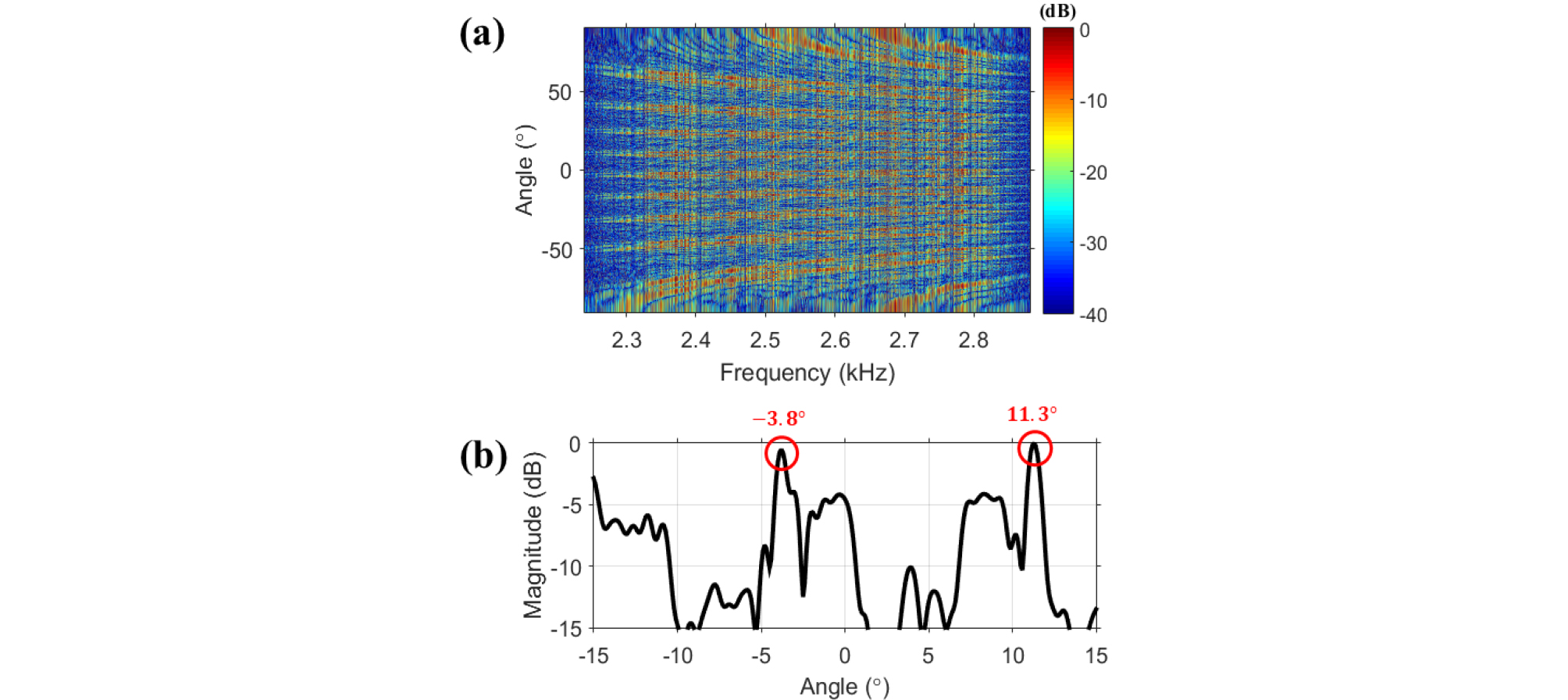
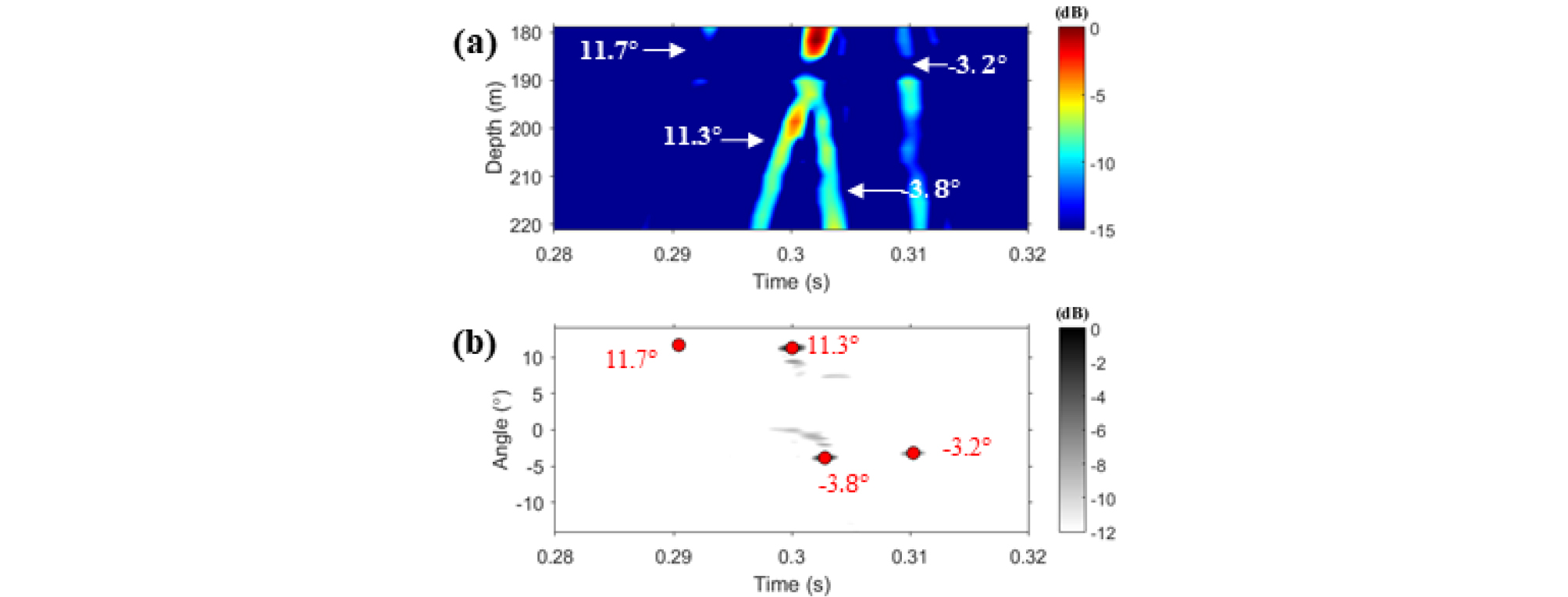
전송 신호의 주파수 대역에 대하여 Eqs. (1)과 (2)에 수직 선 배열 센서를 통해 수신된 신호[Fig. 6(a)]를 적용한다면 주파수 별 빔 형성 결과를 얻을 수 있다[Fig. 7(a)]. Fig. 7(b)는 주파수 별 빔 형성 결과의 비상관 합을 수행한 결과를 나타내며, 이를 통해 지배적인 각도를 추정할 수 있다.

Fig. 7.

Beamforming results; (a) Beam output vs. frequency, (b) incoherent-summed beam output.

Fig. 7(b)로부터 두 개의 지배적인 각도(-3.8°와 11.3°)가 존재함을 확인하였다. 하지만 Fig. 7(a)를 통해서도 알 수 있듯이, 전송 주파수가 설계 주파수보다 9배 이상 크므로 에일리어싱이 발생한다. 따라서 두 개의 지배적인 각도 외에 다른 각도들이 존재하는지 명확하게 확인하기 위해서는 다른 방법이 필요하며, 본 논문에서는 탐침 신호를 통해 추정한 채널 임펄스 응답을 활용하고자 한다.

탐침 신호는 송, 수신단에서 서로 알고 있는 정보이므로, 설계된 탐침 신호와 수신된 탐침 신호를 통해서 채널 임펄스 응답을 추정할 수 있다. 설계된 탐침 신호와 Fig. 6(a)에 나타낸 수신 신호 사이의 정합 필터를 적용하면 Fig. 8(a)와 같은 결과를 얻을 수 있으며, 이는 음원과 수신기 사이의 채널 정보를 의미한다. Fig. 8(a)로부터 두 개 이상의 각도로 음파가 전달되고 있음을 알 수 있으며, 앞서 찾은 각도 외에 나머지 각도를 추정하기 위해 이를 빔-시간 그래프로 나타낸다면 4개의 각도가 지배적임을 알 수 있다[Fig. 8(b)]. Fig. 7(b)와 Fig. 8(b)의 결과를 비교했을 때, -3.2°와 11.8°는 에일리어싱 또는 빔 해상도로 인해 구분할 수 없는 각도에 해당한다. 결과적으로 Fig. 8(b)로부터 추정한 4개의 각도는 4개의 빔 다이버시티가 존재함을 의미한다.

Fig. 8.

(a) Channel Impulse Response (CIR) from the probe signal, (b) Beam-time migration from the CIR.

4.2 빔 다이버시티 결합 기법

Fig. 9(a)는 Fig. 6(b)에 재래식 빔 형성 기법을 적용한 결과를 나타내며, 빔 형성을 위해 사용된 각도는 총 4개로 -3.8°, -3.2°, 11.3°, 11.7° 순서로 빔 번호를 정의하였다(#1 : -3.8°, #4 : 11.7°). Fig. 9(b)는 빔 형성된 신호의 채널 임펄스 응답을 의미하며, 채널 임펄스 응답 추정을 위해 M-sequence 신호를 이용하였다. 1, 2번 빔과 비교했을 때, 3, 4번 빔은 지배적인 경로가 2개인 것으로 보인다. 이를 통해 3, 4번 빔이 1, 2번 빔에 비해 통신 성능이 좋지 않으리라고 예상할 수 있다.

Fig. 9.

(a) Beamformed signal, (b) channel impulse response of beamformed signal (#1:-3.8°, #2:-3.2°, #3:11.3°, #4:11.7°).

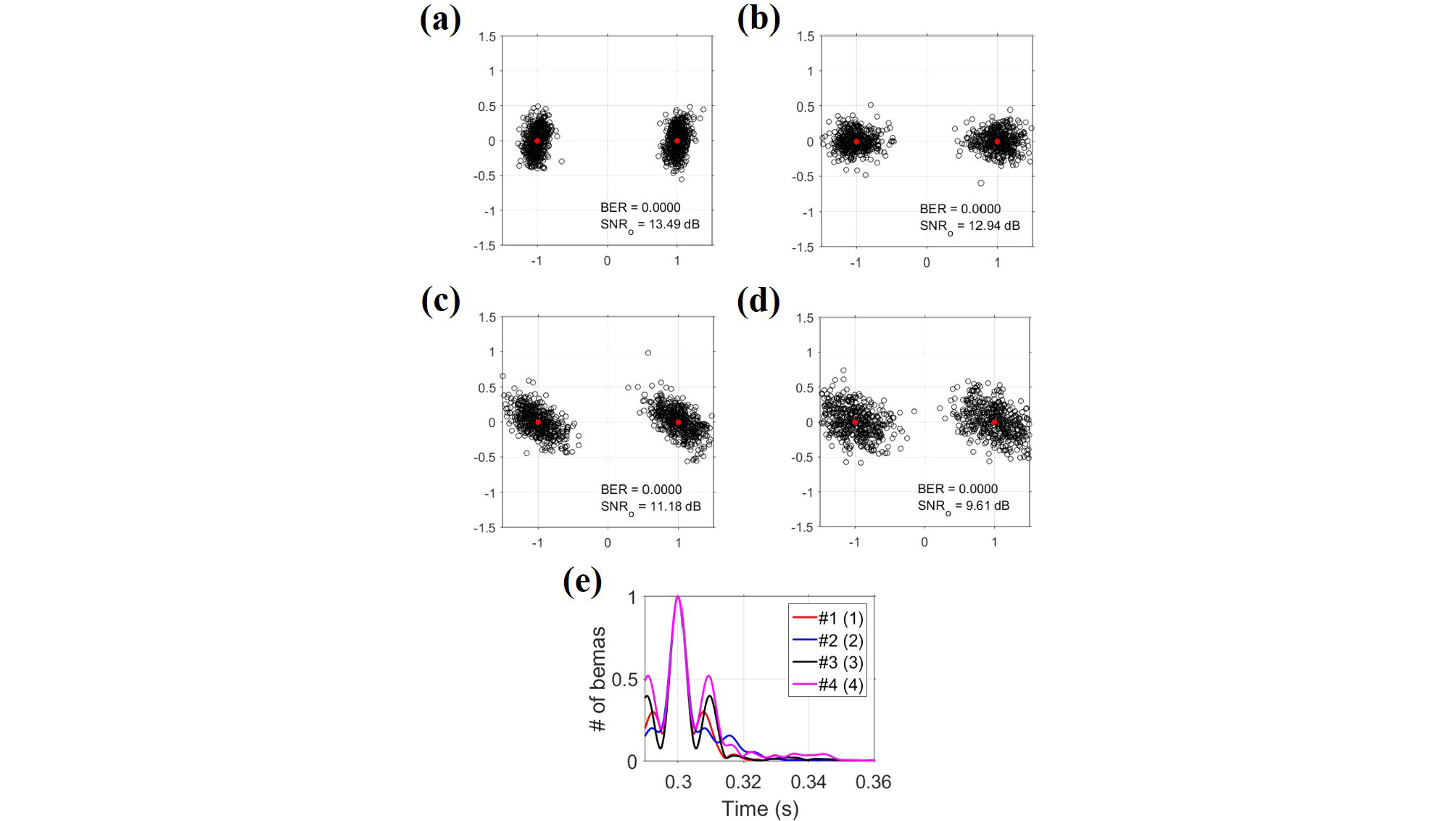
특정 각도로 빔 형성된 신호로부터 통신 성능을 추정할 경우, 이는 빔 다이버시티가 1인 경우에 해당하며 이는 공간 필터라고도 정의할 수 있다. Fig. 10(a)- (d)는 4개의 빔 조향된 신호로부터 수동형 시역전 처리를 이용하여 분석한 통신 성능 결과를 나타낸다. 모든 경우에 대해서 비트 오류율은 0이기 때문에 성능 지표로써 출력 신호 대 잡음비를 활용해야 하며, 1-2-3-4 순으로 출력 신호 대 잡음비가 낮음을 알 수 있다. 수동형 시역전 처리는 궁극적으로 채널 임펄스 응답의 자기상관관계와 관련이 있으므로^{[20], [21]} 이를 이용하여 통신 성능 결과를 분석할 수 있으며, Fig. 10(e)는 각 빔의 채널 임펄스 응답의 자기상관관계 결과를 나타낸 그림이다. 자기상관관계가 델타 함수에 가까울수록 통신 성능이 향상되며, 부엽의 크기는 통신 성능의 저하를 일으킨다. 부엽의 크기는 2번 빔을 제외하고, 1-3-4 순으로 커짐을 알 수 있다. 또한, 2번 빔의 경우 유사한 크기의 부엽이 2개가 있으며, 편의상 두 부엽의 크기를 단순히 더하여 1번, 3번 빔과 비교할 때 2번 부엽의 크기는 1번 빔보다 크고 3번 빔보다 작음을 확인할 수 있다. 따라서 부엽의 크기는 1-2-3-4 순으로 커지며, 이는 출력 신호 대 잡음비 순서와 일치한다.

Fig. 10.

Single beam diversity; (a)-(d) constellation [(a) -3.8°, (b) -3.2°, (c) 11.3°, (d) 11.7°], (e) autocorrelation of channel impulse response obtained from beamformed signals.

Tables 1과 2는 총 4개의 빔에 대해 빔 다이버시티가 각각 2와 3인 경우에 대한 결과를 모든 경우의 수에 대해서 정리한 표이다. 표는 빔 다이버시티 결합 전과 후로 비교하여 나타냈으며, 표로부터 두 가지 경우로 결과로 나뉘는 것을 알 수 있다. 두 가지 경우는 다음과 같다; 1) 조합 전 통신 성능 결과들보다 우수한 통신 성능이 도출되는 경우와 2) 조합 전 통신 성능 결과들 사이의 통신 성능이 도출되는 경우. 2)의 경우 일반적으로 알려진 다이버시티 개수와 통신 성능향상이 비례한다는 사실과 다른 내용이며, 이를 확인하기 위해 앞의 분석과 같이 부엽의 크기를 통하여 분석하기로 한다. 또한, 여러 가지 조합 중 가장 큰 변화가 있는 조합을 대표적으로 선택하여 보여주기로 한다.

Table 1. Output SNR with 2 beams.

Table 2. Output SNR with 3 beams.

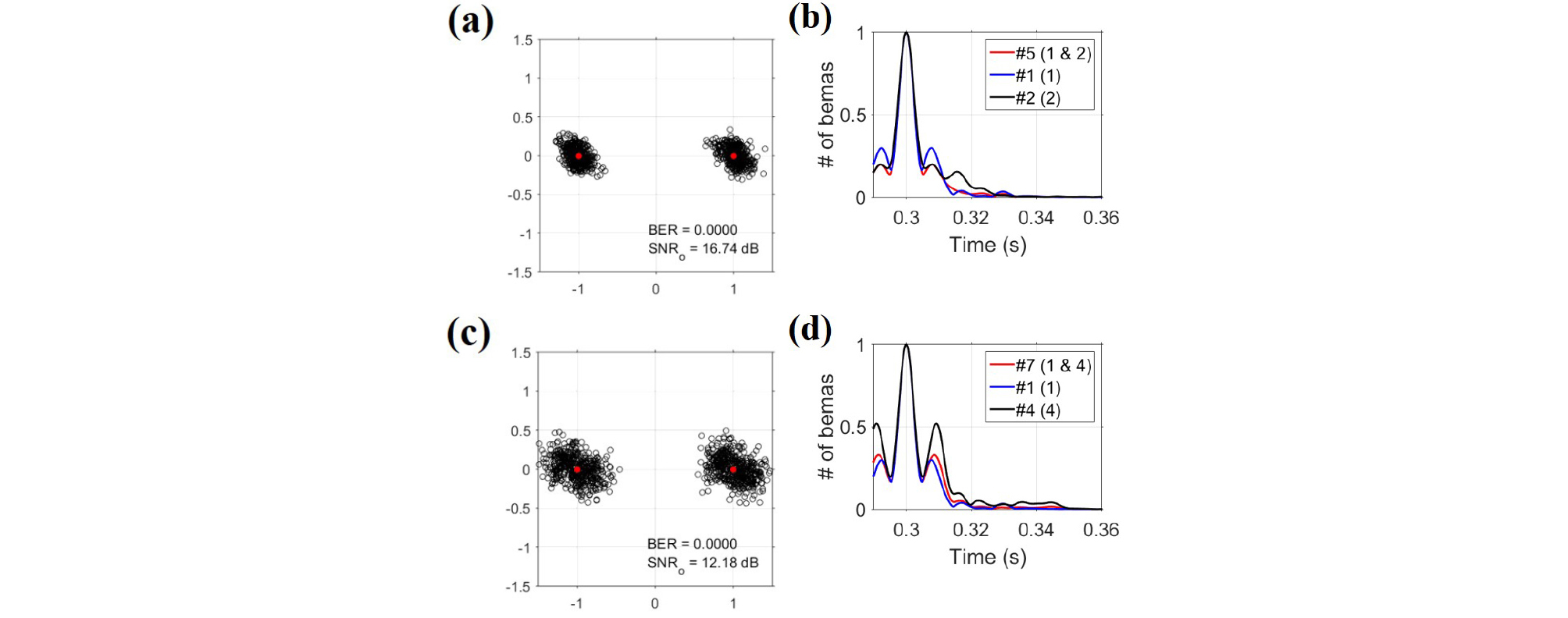
빔 다이버시티가 2인 조합 중 1)의 경우의 대표적인 조합으로는 1번 빔과 2번 빔의 조합이며, 2)의 경우의 대표적인 조합으로는 1번 빔과 4번 빔의 조합이다. 1번 빔과 2번 빔을 조합했을 때, 출력 신호 대 잡음비는 조합 전에 비해 각각 3.2 dB와 3.8 dB만큼 증가했다[Fig. 11(a)]. Fig. 11(b)는 1번 빔과 2번 빔의 조합 효과를 보기 위한 그림이며, 그림으로부터 부엽의 크기는 마치 1번 빔과 2번 빔의 합집합과 같은 효과처럼 감소하는 것을 확인할 수 있다. 이로 인해 1번과 2번 빔 조합이 빔 다이버시티가 2인 조합 중 출력 신호 대 잡음비가 가장 큰 조합임을 확인할 수 있다.

Fig. 11.

Beam diversity combining with 2 beams; (a) and (b):#1 and #2, (c) and (d):#1 and #4, (a) and (c):constellation, (b) and (d):autocorrelation of channel impulse response.

하지만 1번과 4번 빔을 조합했을 때, 4번 빔의 큰 부엽의 영향으로 인해 1번 빔의 부엽보다 큰 부엽의 크기를 갖는 것을 Fig. 11(d)로부터 확인할 수 있다. 이로 인해 조합 후 1번 빔과 4번 빔과 비교하면 출력 신호 대 잡음비는 각각 -1.3 dB와 +2.6 dB 만큼 차이가 발생했다. 즉, 상대적으로 차이가 큰 부엽을 가지는 빔들을 조합한다면, 다이버시티가 증가함에도 통신 성능이 향상되는 방향으로 결과가 도출되지 않게 된다[Fig. 11(c)]. 따라서 이는 다이버시티 결합 시 부엽의 크기를 확인할 필요성이 존재함을 보여준다.

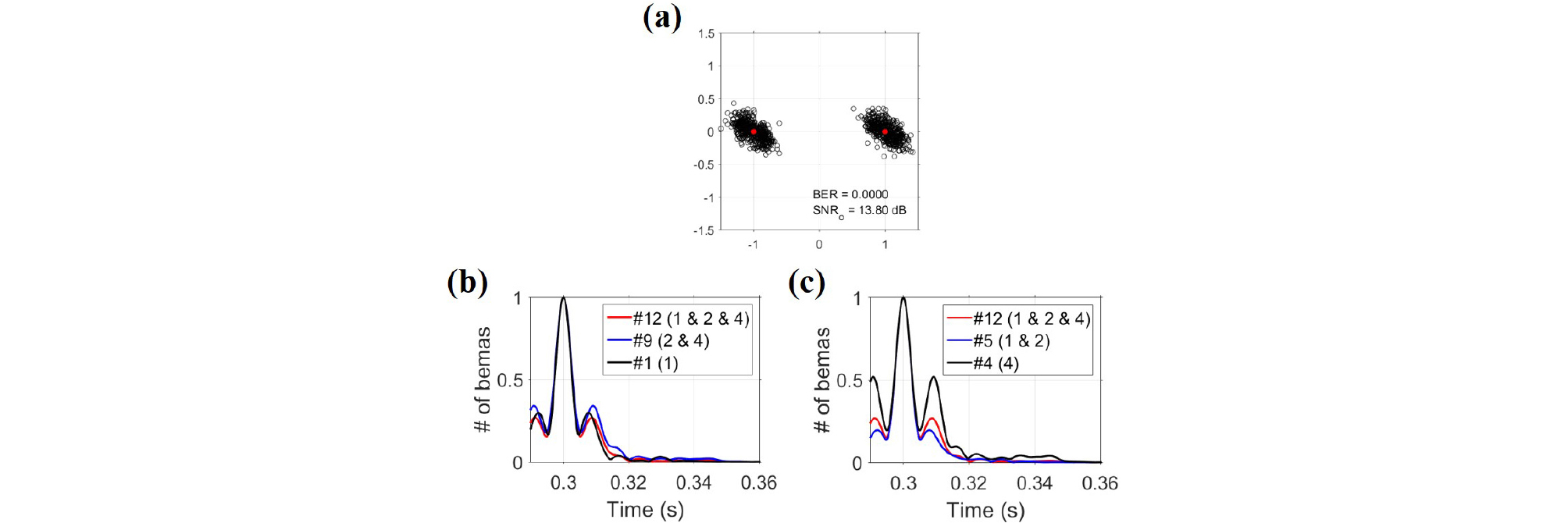
Fig. 12는 빔 다이버시티가 3인 조합 중 대표적인 예시에 관한 결과를 나타내는 그림이다. 1)의 경우를 보여주는 예시는 2번 & 4번 빔과 1번 빔의 조합이며, 1번 & 2번 빔과 4번 빔의 조합은 2)의 예시이다. 1)의 경우, 조합 후 출력 신호 대 잡음비 차이는 2번 & 4번 빔과 1번 빔에 비해 각각 +1.8 dB와 +0.3 dB이며, 2)의 경우는 1번 & 2번 빔과 4번 빔에 비해 각각 -2.9 dB와 +4.2 dB이다. 앞선 분석 결과와 마찬가지로 다이버시티가 3인 경우에도 출력 신호 대 잡음비의 증가 또는 감소량이 부엽의 크기 변화와 일치한다.

Fig. 12.

Beam diversity combining with 3 beams; (a) constellation of #1, #2, and #4, (b) autocorrelation of channel impulse response #2 & #4 and #1, (c) autocorrelation of channel impulse response #1 & #2 and #4.

또한, Fig. 11(a)와 Fig. 12(a)의 비교를 통해 매우 큰 부엽을 가지는 4번 빔이 잡음과 같은 효과를 내어, 다이버시티가 증가할 때 오히려 통신 성능이 저하될 수도 있다는 사실을 확인할 수 있다. 즉, 다이버시티의 증가가 통신 성능의 향상을 의미하지 않는다는 결론을 내릴 수 있다.

V. 결 론

본 논문에서는 심해 30 km 거리의 환경에서 빔 다이버시티 기반의 수동형 시역전 처리를 통해 통신 성능 분석을 수행하였다. 빔 다이버시티 결합을 위해 수직 선 배열에 전달되는 음파의 각도를 추정해야 하며, 이를 위해 수직 선 배열 센서에 수신된 신호로부터 추정한 채널 임펄스 응답을 이용하였다. 채널 임펄스 응답으로부터 계산한 빔-시간 그래프를 통해 30 km 거리의 환경에서 4개의 지배적인 전달 각도를 추정하였다. 추정한 각도들은 곧 빔 다이버시티의 개수를 의미하며, 이를 이용하여 각도의 조합에 따른 통신 성능을 비교하였다.

모든 데이터에 대해서 비트 오류율이 0이었으므로, 성능 비교를 위한 지표로써 출력 신호 대 잡음비를 이용하였다. 데이터 분석 결과로부터 각도 조합에 따라 1) 조합 전 통신 성능 결과들보다 우수한 통신 성능이 도출되는 경우와 2) 조합 전 통신 성능 결과들 사이의 통신 성능이 도출되는 경우, 두 가지 경우로 나뉘는 것을 확인하였다. 본 논문에서는 두 가지 경우에 대해 채널 임펄스 응답 관점에서 해석하였으며, 1)의 경우 이론적인 시역전 처리의 원리와 같이 다이버시티 결합을 통해 주엽 대 부엽 크기 비율이 결합 전 결과들보다 커짐으로써 통신 성능이 향상되는 것으로 나타났다. 하지만 다이버시티 결합에 따라 결합 전의 주엽 대 부엽 크기 비율이 오히려 낮아지는 조합도 나타났으며, 이는 2)의 경우에 해당하는 결과와 대응되는 것으로 확인되었다. 따라서, 빔 다이버시티 결합을 통해 항상 통신 성능이 향상되지 않음을 알 수 있었으며, 빔 다이버시티 결합을 위해서는 각도 조합에 주의해야 함을 확인하였다. 또한, 부엽은 결국 빔 조향 시 빔 조향 각도가 아닌 다른 각도에 의한 신호의 결과로 추정할 수 있으며, 적응형 빔 형성 기법을 적용할 경우 통신 성능이 향상될 것으로 기대된다.