I. 서 론
최근 해양 물체들(e.g., 잠수함, 선박)로부터 방사되는 신호에서 토널 신호 성분을 검출하는 연구가 많은 관심을 받고 있다. 각각의 해양 물체들은 고유의 토널 주파수를 가지기 때문에 토널 주파수를 정확히 탐지하는 것은 물체를 식별하는데 매우 중요하다.
특정 신호의 주파수를 검출하는 전통적인 방법으로는 이산 푸리에 변환(Discrete Fourier Transform, DFT)을 사용하는 방법이 있다.[1] 이 기법의 한 가지 단점은 관측 시간이 적을 때 검출할 수 있는 주파수의 해상도가 낮다는 점이다. 즉, 탐지할 수 있는 주파수 사이의 간격이 넓다는 것이다. 이러한 단점을 보완하기 위해 matrix pencil,[2] root-MUSIC[root-MUltiple SIgnal Classification(root-MUSIC)],[3] 그리고 ESPRIT(Estimation of Signal Parameters via Rotational Invariance Techniques)[4] 등과 같은 기법들이 제시되었다. 이 기법들은 신호 공간(신호 벡터의 공분산 행렬)의 고유 벡터를 이용하여 토널 주파수를 탐지한다. 이산 푸리에 변환을 사용하는 방법에 비해, 이 기법들은 적은 수의 관측 시간으로도 높은 주파수 해상도를 보인다. 그러나 신호 공간의 고유 벡터를 구하는데 많은 계산이 필요하고 토널 신호를 구성하는 주파수 성분의 개수를 사전에 알아야 한다는 단점이 있다. 이산 푸리에 변환의 단점을 보완하는 또 다른 방법으로는 압축센싱 기반 기법들이 있다.[5], [6], [7] 압축센싱의 기본 철학은 복원하고자 하는 신호가 적은 수의 원소만 의미 있는 값을 갖는(대부분의 원소가 0인) 희소신호인 경우, 신호의 차원보다 적은 수의 관측 데이터로도 정확한 복원이 가능하다는 것이다. 토널 신호를 구성하는 주파수 성분의 수는 전체 주파수 대역과 비교했을 때 희소하므로, OMP(Orthogonal Matching Pursuit), SOMP(Simultaneous OMP) 알고리듬 등의 압축센싱 기법이 토널 주파수 검출에 사용되었다. 그러나 이 기법들 또한 토널 주파수 성분의 수를 필요로 하고, 이산(discrete) 주파수 영역에서 토널 주파수를 검출하기 때문에 basis mismatch error 문제가 불가피하다.
본 논문에서는 ANM(Atomic Norm Minimization)[8], [9]을 이용한 새로운 토널 주파수 검출 기법을 제안한다. 제안하는 기법의 특징은 연속(continuous) 주파수 영역에서 토널 주파수를 검출한다는 것이다. 따라서 basis mismatch error 문제를 해결할 수 있고, 그 결과 검출된 주파수와 실제 주파수의 오차 또한 줄일 수 있다. 모의실험을 통하여 제안하는 기법이 기존의 기법들에 비해 정확성과 평균 제곱 오차 측면에서 우수한 성능을 보임을 확인하였다.
II. 수중 방사 신호의 모델
수동 소나에서 수신되는 선박의 방사 신호는 크게 4가지로 분류 될 수 있다[10]. 첫 번째 신호 성분은 기함의 엔진, 기어박스, 보조 장치 등 다양한 기계류 장치에 의해 발생되는 토널 신호이다. 토널 신호는 주로 저주파수 성분들로 구성되어 있다. 두 번째 신호 성분은 유체역학적인 소음 신호로 선박이 이동할 때 함체와 물의 마찰로 발생하는 신호이다. 세 번째 신호 성분은 프로펠러의 회전에 의해 발생하는 공기방울이 터지면서 발생하는 케비테이션 신호이다. 케비테이션 신호는 고주파 대역에서 광대역 특성을 가진다. 마지막 네 번째 신호 성분은 바다 안에서 일어나는 환경 소음이다. 해양의 표면에서 생기는 소음이나 난류 또는 해저면의 지각활동으로 인한 소음 등을 모두 환경 소음이라 한다. 일반적으로 선박의 방사 신호는 4가지 신호 성분을 모두 포함하지만, 본 논문에서는 케비테이션 신호 성분이 없는 상황을 가정한다(선박이 저속운행 하거나 잠수함인 경우 이 가정이 성립한다). 토널 신호와 유체역학적 소음, 주변 환경소음만 존재할 경우, 방사신호 는 다음 Eq. (1)과 같이 표현된다.
| $$s(t)=\sum_{m=1}^kA_m\cos(2\pi f_mt+\phi_m)+a(t).$$ | (1) |
Eq. (1)에서 은 각각 번째 토널 성분의 진폭, 주파수, 위상을 나타내고 는 유체역학적 소음과 환경 소음을 종합한 주변 소음 신호이다. 방사신호 로부터 토널 주파수 을 연속 주파수 영역에서 검출하는 기법을 제안하는 것이 본 논문의 목표이다.
III. ANM(Atomic Norm Minimization) 기반 토널 주파수 탐지 기법
토널 주파수를 검출하기 전에 방사신호 의 토널 신호 성분을 강화하기 위해 세 가지 전처리과정(preprocessing)을 거쳤다. 첫째로, 방사신호를 저역 통과 필터에 통과시켰다. 토널 신호는 저주파 대역에 존재하기 때문에 저역 통과 필터를 통해 토널 신호 성분은 유지하면서 고주파 잡음 성분을 억제시켰다. 둘째로, 데시메이션(decimation)을 통해 측정 데이터의 수를 줄였다. 제안하는 기법은 계산 복잡도가 높은 convex optimization에 의존하는데 데이터의 수를 줄임으로서 토널 주파수 탐지에 필요한 계산량을 감소시켰다. 마지막으로, 자기상관필터에 신호를 통과시켰다. 이를 통해 토널 신호 성분의 주기성은 강화하면서 저주파 대역에 섞인 유체역학적인 소음과 환경소음을 억제할 수 있다. 세 가지 전처리과정을 거쳐서 나온 신호 의 번째 성분은 다음 Eq. (2)와 같다.
| $$r_l=\sum_{m=1}^kA_m\cos(2\pi\frac{f_m}{\alpha f_s}l)+w_l,l=0,1,\cdots,N-1.$$ | (2) |
위 Eq. (2)에서 은 샘플 수, 은 자기상관필터에 유체역학적 소음과 환경 소음을 통과시켰을 때의 아웃풋의 합을 나타낸다. 또한 는 각각 데시메이션 비율과 샘플링 주파수를 나타낸다.
이제 전처리과정을 거쳐 얻은 신호 로부터 토널 주파수 를 복원하는 기법을 제안한다. 제안하는 기법의 가장 큰 특징은 ANM을 이용하여 연속 주파수 영역에서 토널 주파수를 검출한다는 것이다. ANM의 설명을 위해, 다음 Eq. (3)과 같이 atom 을 정의하였다.
| $$\lbrack\overrightarrow a(f,\phi)\rbrack_l=\exp(j(2\pi fl+\phi)),l=0,\cdots,N-1.$$ | (3) |
위 Eq. (3)에서 이고(연속 영역 에서의 임의의 값) 이다. Eq. (3)과 같이 atom을 정의하면, 은 atom들의 선형 결합으로 다음 Eq. (4)과 같이 표현할 수 있다.
| $${\vec{r}} = \sum _{m=1} ^{2k} |c _{m} | {\vec{a}} ( \frac{f _{m}} {\alpha f _{s}} , \phi _{m} )+ {\vec{w}}.$$ | (4) |
을 구성하는 주파수 성분의 수()는 전체 주파수 대역 과 비교했을 때 희소하다. 주파수 측면에서 신호가 희소한 경우, 희소 신호 가 다음 Eq. (5)의 해를 통하여 복원할 수 있음이 밝혀졌다.[8]
| $$\min\nolimits_\overrightarrow x\;\;\frac12\vert\vert\overrightarrow r-\overrightarrow x\vert\vert_2^2+\tau\vert\vert\overrightarrow x\vert\vert_{A,1}.$$ | (5) |
위 Eq. (5)에서 는 를
| $$A=\{\overrightarrow a(f,\phi):f\in\lbrack0,1\rbrack,\phi\in\lbrack0,2\pi)\}$$ | (6) |
의 원소들의 양의 선형 결합으로 나타냈을 때 그 계수들의 합의 최솟값이다. 즉,
이다. 을 atomic norm이라 부르고, Eq. (5)는 잡음에 의한 효과를 고려함()과 동시에 atomic norm()을 최소화하는 문제이므로 ANM(Atomic Norm Minimization) denoising 문제라 불린다.
Eq. (5)의 목적함수는 atomic norm 을 포함하므로, LP(Linear Programming), SDP(Semi-Definite Programming)와 같은 잘 알려진 convex solver에 문제를 바로 대입시킬 수 없다. 따라서 특정 solver의 입력 형식에 맞게 목적함수의 꼴을 바꿔주어야 한다. Eq. (5)를 SDP solver에 적합한 꼴로 바꾸면 다음과 같다.[9]
위 Eq. (8)에서 Toep는 퇴플리츠(Toeplitz) 작용소를 나타내고 는 임의의 행렬이다. Bhaskar et al.[9]는 SDP solver로 구한 Eq. (8)의 해 가 다음 성질을 가지고 있음을 보였다.[9]
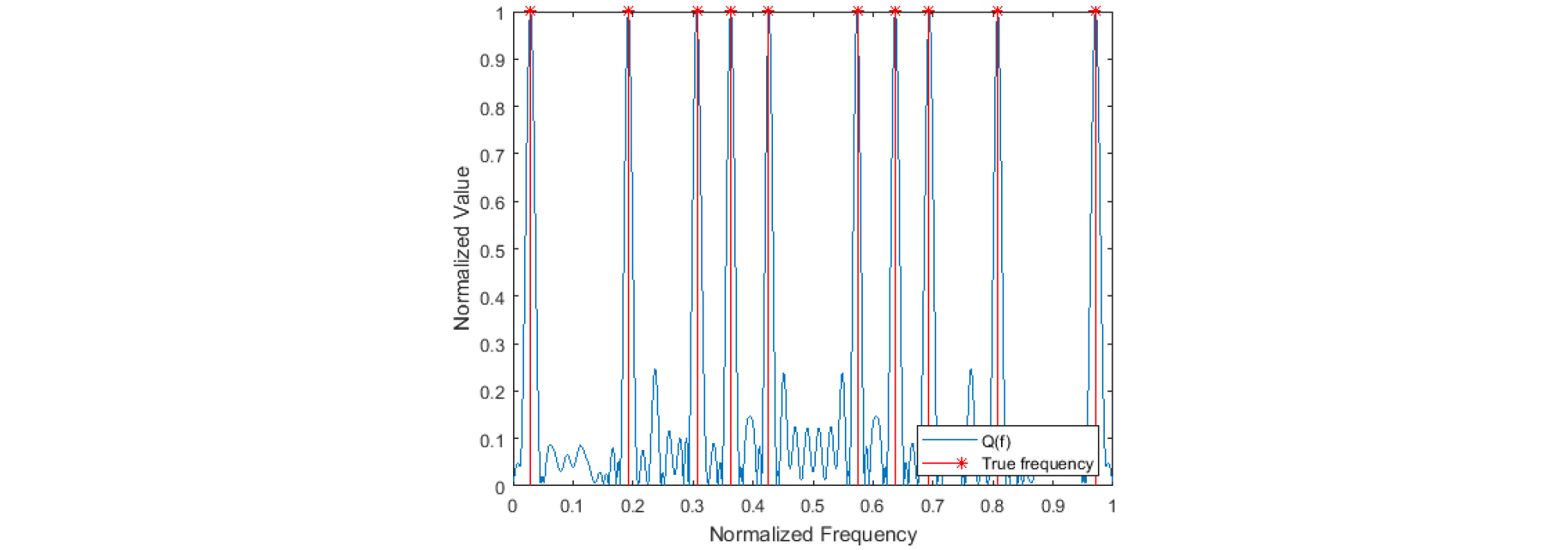
즉, 로 정의했을 때 토널 주파수 에 대해서는 가 성립하고 그 외의 주파수에 대해서는 가 성립한다. 따라서 를 주파수 에 대하여 도시화한 후, 가 되는 를 구함으로써 최종적으로 토널 주파수들을 검출해낼 수 있다(Fig. 1 참조).
전처리과정을 포함한 제안하는 토널 주파수 검출 기법을 블록 다이어그램으로 나타내면 Fig. 2와 같다.
IV. 모의실험
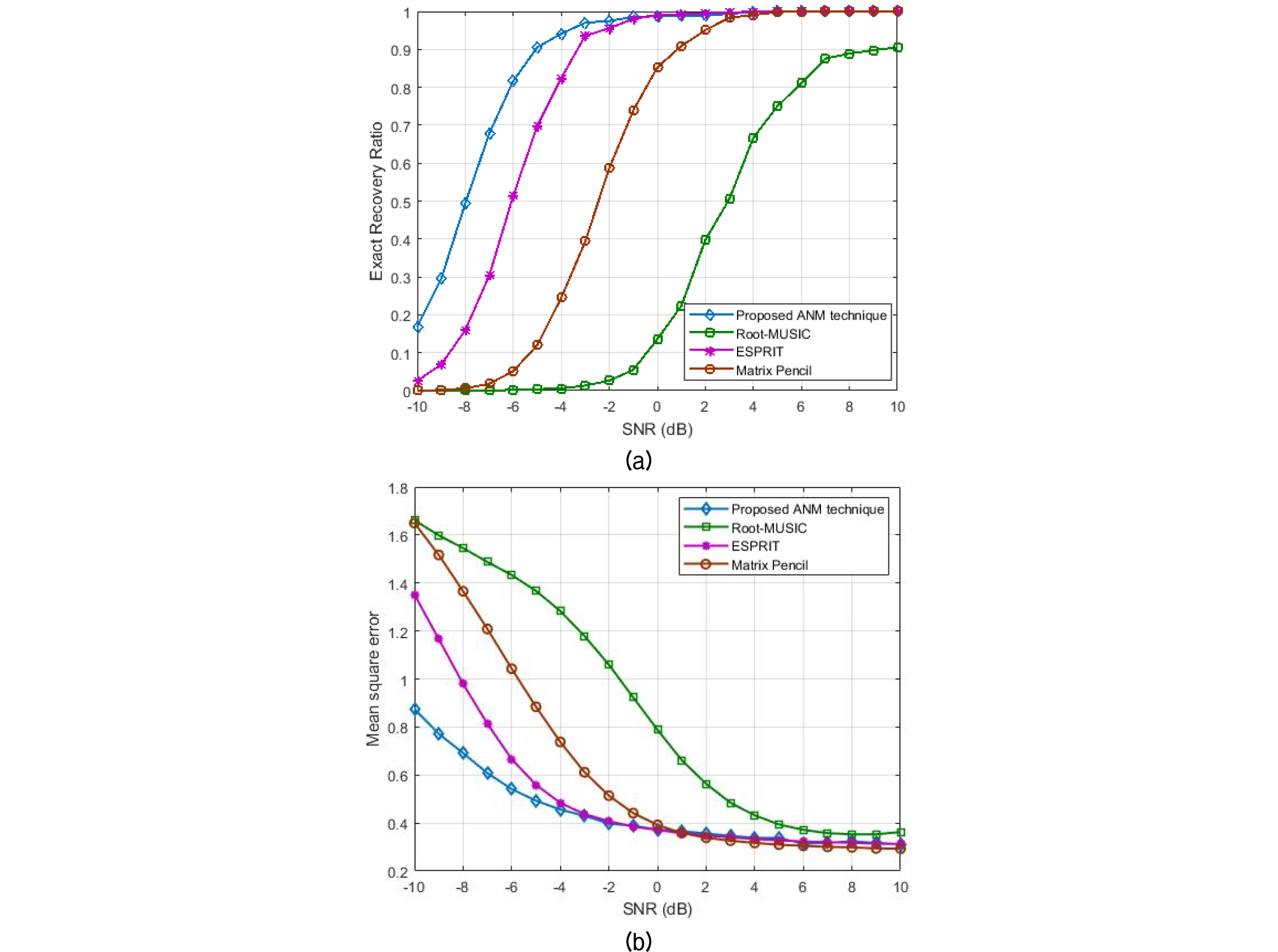
본 논문에서 제안한 토널 주파수 검출 기법의 성능을 모의실험을 통하여 확인하였다. 모의실험을 진행하기 위해 방사신호 를 Eq. (1)에 맞게 생성하였다. 토널 주파수는 총 10개, 500 Hz이내에서 랜덤하게 생성하였으며, 주변 소음 신호 는 white Gaussian noise로 하였다. 샘플링 주파수 는 10 kHz로 설정하였고 저역 통과 필터의 차단주파수(cutoff frequency)를 500 Hz로 설정하였으며, 데시메이션 비율은 로 하였다. 비교를 위해 제안하는 기법과 더불어 root MUSIC, matrix pencil, ESPRIT 기법에 대해서도 모의실험을 실시하였다. 모의 실험에서 root MUSIC의 파라미터(신호 수)는 20으로 ESPRIT의 공분산 크기 파라미터는 50으로 설정하였다. -10 dB에서 10 dB 사이의 SNR(Signal-to-Noise Ratio) 영역에서 각각의 기법에 대하여 2,000번의 모의실험을 실시한 후, 복원률(Exact Recovery Ratio, ERR)과 평균 제곱 오차(Mean Square Error, MSE)를 평균 내었다. 모든 토널 주파수를 정해진 오차 범위[1/n; FFT(Fast Fourier Transform)의 해상도] 내에서 검출했을 경우를 성공으로 정의할 때 복원률은 다음 Eq. (8)을 이용하여 구할 수 있다.
| $$\mathrm{ERR}=\frac{\mathrm{Number}\;\mathrm{of}\;\mathrm{success}}{\mathrm{Number}\;\mathrm{of}\;\mathrm{totaltrials}}.$$ | (10) |
모의실험 결과를 Fig. 3에 나타내었다. Fig. 3(a)에는 SNR에 따른 각각의 기법의 복원률을 나타내었고, Fig. 3(b)에는 SNR에 따른 각각의 기법의 평균제곱오차를 나타내었다. 제안하는 ANM 기반 토널 주파수 검출 기법이 낮은 SNR 영역(-10 dB ≦ SNR ≦ 2 dB)에서 기존의 기법보다 높은 복원률, 낮은 평균제곱오차를 보임을 확인할 수 있다. 예를 들어 SNR이 -8 dB일 때 기존 기법들의 복원률은 0.2보다 낮은 반면 제안하는 ANM 기반 기법의 복원률을 0.5임을 관찰할 수 있다. 이는 이산 주파수 영역에 기반한 기존 기법들과 달리 ANM 기반 기법은 연속 주파수 영역에서 토널 주파수를 검출하여 basis mismatch error를 완화시킬 수 있기 때문이다.
V. 결 론
본 논문에서는 ANM을 이용하여 토널 주파수를 검출하는 기법을 제안하였다. 기존 압축센싱 기반 토널 주파수 검출 기법들은 주파수 영역의 이산화(discretization)에 의존하기 때문에 basis mismatch error가 불가피하다. 그러나 제안하는 기법은 연속 주파수 영역에서 직접 토널 주파수를 검출하기 때문에 basis mismatch error를 완화시킬 수 있고, 검출된 주파수와 실제 주파수 사이의 오차를 줄일 수 있다. 모의실험을 통하여 제안하는 기법이 기존의 기법보다 복원률과 평균제곱오차 측면에서 더 우수한 성능을 보임을 확인하였다. 한 가지 언급하고 싶은 점은 ANM 기반 기법은 SDP solver에 의존하기 때문에 계산 복잡도가 기존 기법들에 비해 높다는 것이다. 연속 주파수 영역에서 최적화 기법에 의존하지 않고 토널 주파수를 검출하는 기법을 개발하여 basis mismatch error와 높은 계산 복잡도 문제를 동시에 해결하는 것은 하나의 중요한 후속 연구이다.