I. 서 론
II. 3차원 음향 인텐시티 벡터를 통한 음원 위치 추정법
2.1 3차원 음향 인텐시티 계산
2.2 유한 차분 및 위상 부정합에 의한 오차
2.3 위치추정 편향 오차
III. 음파 도달시간차 계산을 통한 음원 위치 추정법
3.1 도달시간차 계산 방법
3.2 센서 간격 및 샘플링 주파수에 따른 오차
IV. 헬름홀츠 수에 따른 위치추정 오차의 비교
V. 음원 위치추정 실험결과 비교
5.1 마이크로폰 간격에 따른 위치추정 실험
5.2 잔향음장 내 위치추정 실험
VI. 결 론
I. 서 론
음원의 위치추정은 정밀한 소음제어 또는 IoT (Internet-of-Things) 기반으로 활용되어지는 사용자-기계간의 상호 작용을 높이기 위해 요구되는 기술이며, 광학이나 전자기적으로 식별이 힘든 장치에서 발생되는 음향을 이용해 음원 추적을 하는 데에도 적용될 수 있다. 근거리 음장에서의 음원의 위치를 추정하기 위하여 Near-field Acoustic Holography(NAH) 방법이 대표적으로 사용되며,[1],[2] 원거리 음장에서의 음원의 위치를 추정하는 방법으로 도달시간차(Time Difference of Arrival, TDoA),[3],[4] 빔포밍(beamforming),[5],[6] MUltiple SIgnal Classification(MUSIC)[7],[8] 등의 방법이 대표적으로 사용되어지고 있다.
도달시간차 계산을 통한 위치추정 방법은 음파가 마이크로폰에 도달하는 시간지연 차이를 통해 계산되는 상호상관함수로부터 음원의 위치를 계산하는 방식이며, 특히 Generalized Cross Correlation-Phase transform(GCC-PHAT)[3]는 잡음이나 잔향이 고려되는 환경에서도 강건한 특성을 나타내는 것으로 알려져 있다. 그러나 양자화 오차[9]를 줄이기 위해서 샘플링 주파수가 높아야하고 수음점 사이의 간격이 멀어야 하는 한계점이 있다. 빔포밍은 각 마이크로폰으로부터 받은 신호의 위상 조정을 통해 빔을 형성하여 각 방위별로 신호세기를 비교하여 위치추정을 하는 방법이며, 배열을 구성하는 다수의 마이크로폰을 활용하여 비 상관 잡음의 크기를 낮출 수 있다는 특징이 있다. 그러나, 낮은 주파수 대역을 갖는 음원에 대해서는 빔 폭이 넓어져서 정확한 위치추정이 힘들다는 한계점이 있다. MUSIC은 수신 신호의 공분산행렬의 고유값 분해를 통해 계산되어지는 잡음 부 공간 및 신호 부 공간의 직교성을 이용하는 방법으로, 높은 공간 분해능을 가지는 장점이 있다. 그러나, 입사되는 신호가 코히어런트한 경우에는 행렬의 랭크가 감소하여 잡음 부 공간을 구할 수 없는 점, 그리고 복잡한 비 정방 행렬 계산과정으로 인하여 효율성이 떨어지는 한계점이 있다.
도달시간차 또는 빔포밍을 실제로 적용하여 높은 정확도를 얻기 위해서는 다수의 마이크로폰이 필요하고, 가용한 주파수 대역폭을 넓히기 위해서 배열의 크기가 커져야 하므로, 이는 실질적 응용 범위를 제한하는 사항이 된다. 이러한 한계를 극복하기 위한 또 다른 방법으로, 음향 인텐시티법이 있다.[10],[11],[12] 이는 두 개의 마이크로폰 사이에서 계산된 음압 및 입자속도를 통해 인텐시티 벡터를 계산하여 음원의 위치를 추정하는 방법이며, 수음점 사이의 간격이 줄어들수록 유한차분오차도 줄어들기 때문에 하드웨어 소형화에 유리한 장점이 있다.[13] 이미 오래전에 개발된 방법임에도 불구하고 계측된 신호가 지니는 매우 큰 편향오차에 의해 근접음원을 제외하고는 그 적용이 제한되어왔으나, 최근에는 이러한 오차를 보상하는 방법에 대한 연구가 진행되고 있으며[14],[15],[16],[17],[18] 따라서 소형의 마이크로폰 배열을 통해 원거리 음장에서의 음원의 위치를 정확하게 추정할 수 있는 가능성이 확보되고 있다.
본 논문에서는 정사면체 형태의 3차원 마이크로폰 배열을 통해 계산된 음향 인텐시티 벡터 및 음파의 도달시간차를 기반으로 원거리 음장에서 전파되는 음원의 위치추정 방법에 대해 논의하고 위치추정 결과에서 나타나는 오차[15],[16],[17],[18]에 대해 설명한다. 마이크로폰 간격 변화에 따라서 위치추정 실험결과를 분석 및 비교하여, 음향 인텐시티 벡터를 적용하여 시스템을 소형화 할 수 있는 이점에 대해 논의한다. 마지막으로 인텐시티 벡터를 통한 음원 위치추정 방법의 실질적인 유효성을 검증하기 위해서 잔향음장 내에서 실험한 결과에 대해 설명한다.
II. 3차원 음향 인텐시티 벡터를 통한 음원 위치 추정법
II. 3차원 음향 인텐시티 벡터를 통한 음원 위치 추정법음향 인텐시티는 에너지의 크기와 방향에 대한 정보를 모두 포함하므로, 특정 음원에 의해 형성된 음장에서 인텐시티 벡터를 계산하면 음원의 위치를 추정할 수 있게 된다. 조화음장에서 음향 인텐시티를 다음과 같은 식으로 나타낼 수 있다.[12]
| $${\boldsymbol I}_{\mathbf a}(\omega)=Re\left\{{\boldsymbol G}_{\mathbf{pu}}(\omega)\right\},$$ | (1) |
여기서 이고, 는 단일 방향의 상호 파워스펙트럼 밀도함수(Cross-Power Spectral Density Function, CPSD)를 나타낸다. 두 마이크로폰 사이에서 계측된 음압을 통해, 입자속도를 선형화된 오일러 공식에 의해 근사화할 수 있으며, 정상 음장에서 음향 축 방향의 1차원 능동 음향 인텐시티 성분은 서로 다른 두 마이크로폰으로 계측된 음압의 CPSD로 표현된 식으로 정리할 수 있다.[12]
| $$I_w(\omega)=\frac{-1}{\rho_0\omega d}Im{\left\{{\boldsymbol G}_{{\mathbf p}_{\mathbf1}{\mathbf p}_{\mathbf2}}(\omega)\right\}.}$$ | (2) |
는 조화음장에서 나타낸 1차원 능동 음향 인텐시티를 나타낸다. 여기서, 는 유체의 밀도, 는 마이크로폰 사이의 간격, 그리고 는 마이크로폰으로부터 계측되어진 음압신호의 CPSD 이다. 따라서 두 마이크로폰 사이의 CPSD 계측을 통해 1차원 능동 음향 인텐시티를 계산할 수 있다.
2.1 3차원 음향 인텐시티 계산
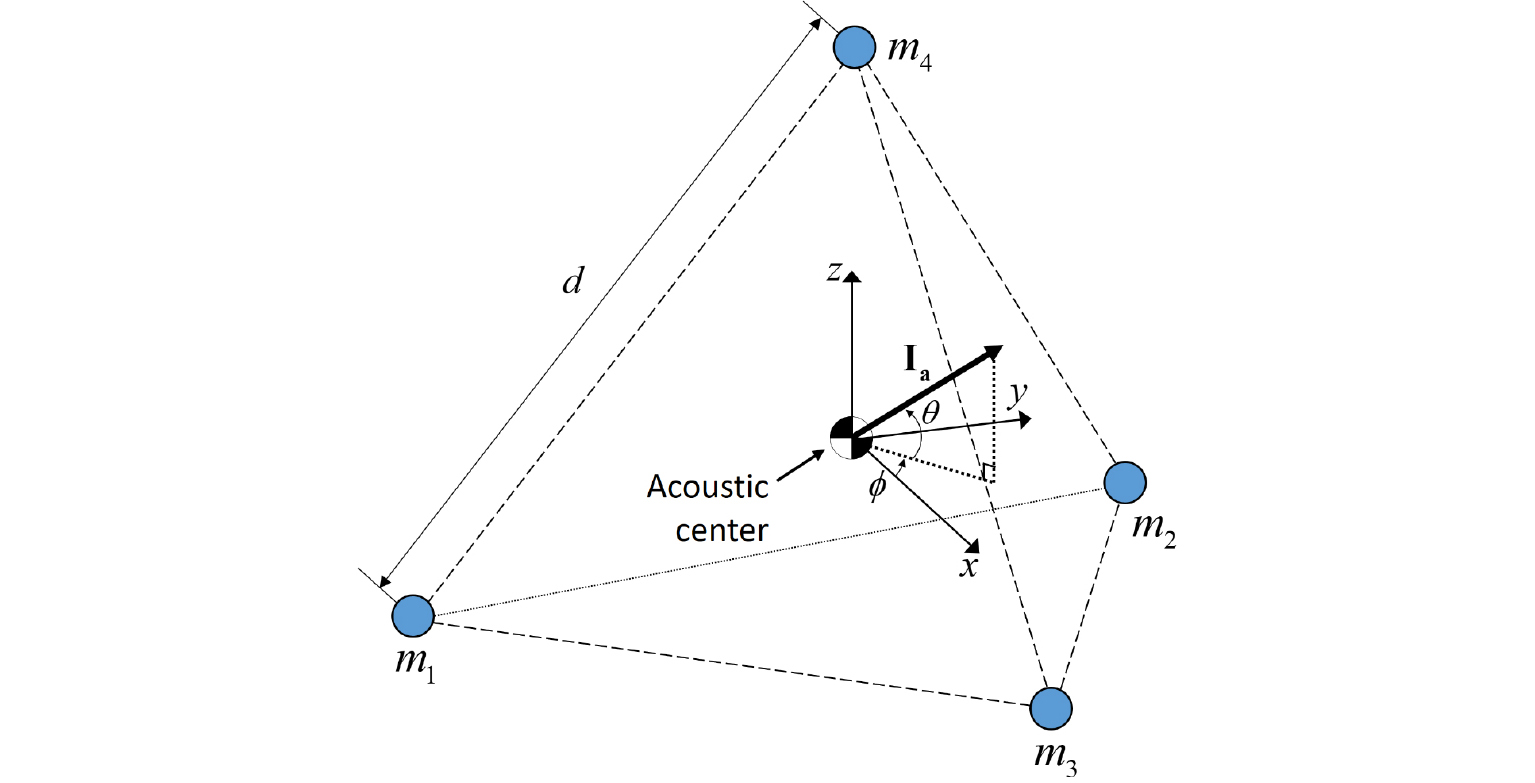
3차원 음향 인텐시티를 구하기 위해서는 동일한 평면상에 존재하지 않는 4개 이상의 마이크로폰으로 구성된 마이크로폰 배열 시스템이 필요하며, 본 연구에서는 3차원 음향 인텐시티를 계산하기 위해서 Fig. 1과 같은 정사면체 마이크로폰 배열구조를 사용하였다.[19],[20] 정사면체 배열은 마이크로폰 사이의 간격이 동일하므로 유한차분법에 따른 오차를 동일하게 통제 할 수 있고, 무지향성이 높으며, 3차원을 표현할 수 있는 가장 적은 개수의 마이크로폰을 사용한다는 장점을 가지고 있다.[20]
정사면체 모듈을 이용하여 음원의 위치를 추정하기 위해 정사면체의 기하중심과 음향중심을 동일하게 정의하였다. 마이크로폰 사이의 거리가 인 정사면체 배열의 음향중심에서 계산된 3차원 음향 인텐시티는 다음과 같다.[20]
| $${\boldsymbol I}_{\mathbf a}(\omega)=I_{ax}(\omega)\boldsymbol i+I_{ay}(\omega)\boldsymbol j+I_{az}(\omega)\boldsymbol k,$$ | (3) |
여기서
음원의 3차원 위치 추정은, Fig. 1에서 나타낸 것과 같이 음향 중심으로부터 음원의 방위각 및 고도각을 계산함으로써 이루어진다. 따라서 Eqs. (4) ~ (6)을 통해 계산된 음향 인텐시티의 벡터성분으로 다음과 같이 추정된 방위각과 고도각을 다음의 식으로 표현할 수 있다.
| $${\widehat\phi}_{AI}(\omega)=\tan^{-1}(I_{ay}/I_{ax}),$$ | (7) |
| $${\widehat\theta}_{AI}(\omega)=\tan^{-1}(I_{az}(\omega)/\sqrt{I_{ax}(\omega)^2+I_{ay}(\omega)^2}),$$ | (8) |
여기서, , 은 음향 인텐시티 벡터를 통해 추정된 음원의 방위각 및 고도각을 나타낸다.
2.2 유한 차분 및 위상 부정합에 의한 오차
유한차분 근사화를 통해 입자속도를 구하는 과정에서, d에 비해 입사되는 음파의 파장 길이가 짧을수록 유한차분오차가 극대화 될 수 있다. 따라서 d 에 의해 측정할 수 있는 유효한 상단 주파수가 제한된다. 또한 마이크로폰의 내재적인 위상 부정합은 낮은 주파수 대역에서 인텐시티 계산 오차를 유발하며 이는 유효한 하단 주파수를 제한한다. 자유음장 내 단일 평면파가 두 개의 마이크로폰에 입사될 때, 유한차분오차 및 위상 부정합에 의한 오차는 이미 잘 알려져 있으며, 다음의 식으로 나타낼 수 있다.[11],[12]
| $$\epsilon_I\approx10\log_{10}\left(\frac{\sin(kd)}{kd}\right)+10\log_{10}\left(\frac{kd+\psi_i}{kd}\right),$$ | (9) |
여기서 는 파수를 나타내고, 는 마이크로폰 간격에 관한 헬름홀츠(Helmholtz) 수이며, 는 마이크로폰 간의 위상 부정합 오차를 나타낸다.
Eq. (9)을 통해, 가 커질수록 유한차분오차가 증가하며, 위상 부정합에 의한 오차는 가 낮은 대역에서 집중되는 것을 알 수 있다. 따라서 낮은 주파수 대역에서의 오차를 줄이기 위해서는 마이크로폰 사이의 위상교정이 필수적으로 선행되어야 한다. 또한, 유한차분오차를 고려하여 유효한 상단주파수 및 를 결정해야 함을 알 수 있다.
2.3 위치추정 편향 오차
잔향음장에서 음향 인텐시티 벡터를 계산하는 경우, 벽면 반사와 같은 코히어런트 잡음에 의해서 주파수 편향오차가 발생 한다.[15],[16],[17] 이는 특정한 주파수 변동 주기를 가지는 조화 함수 형태의 오차이며, 주파수 변동 주기는 음원과 수음점간의 간격 및 벽면에 반사하는 음선의 길이 차이에 반비례 한다. 또한, 음파가 마이크로폰 배열에 입사하는 방향에 따라 위치추정 결과가 왜곡되어 나타나는 공간편향오차가 관찰 된다.[16],[17],[18] 이러한 방향 특성은 마이크로폰 배열 구조에 따라 결정되며, 가 증가함에 따라 오차가 커지는 경향성을 나타낸다.
III. 음파 도달시간차 계산을 통한 음원 위치 추정법
3.1 도달시간차 계산 방법
마이크로폰 배열에 도달하는 음파의 시간 차이를 계산하면 음원의 위치를 추정할 수 있다. 따라서 자유음장조건에서 두 마이크로폰 사이의 상호상관함수를 계산함으로써 시간지연을 간단히 계산할 수 있으므로 위치추정 시간이 빠르고 직관적인 결과 해석이 가능하다는 장점을 갖는다.
평면파 입사에 대하여 두 마이크로폰 간의 도달시간지연차는 다음의 식으로 표현할 수 있다.
| $${\boldsymbol d}_{\mathbf a\mathbf b}\boldsymbol\cdot\boldsymbol s=c{\widehat\tau}_{ab},$$ | (10) |
여기서 는 마이크로폰 a, b 의 위치벡터, 는 마이크로폰 배열의 음향중심에서 음원으로의 방향벡터, c는 음속, 그리고 는 두 마이크로폰 a, b 사이에서 계산되는 음파의 도달 시간 차이를 나타낸다. 음원 위치 추정을 수행하기 위해서는 마이크로폰 배열로부터 계산된 다수의 시간지연 값을 토대로 를 계산하여, 이에 대한 x, y, z 성분(,,)을 통해 최종적으로 음원의 방위각과 고도각을 계산할 수 있다. 도달시간차 계산을 통해 추정된 음원의 방위각 및 고도각은 다음의 식으로 표현할 수 있다.
| $${\widehat\phi}_{TDOA}=\tan^{-1}(s_y/s_x),$$ | (11) |
| $${\widehat\theta}_{TDOA}=\tan^{-1}(s_z/\sqrt{s_x^2+s_y^2}).$$ | (12) |
3.2 센서 간격 및 샘플링 주파수에 따른 오차
샘플링 주파수는 음파 도달시간차를 통한 위치추정의 공간해상도를 결정하므로, 정확도를 향상시키기 위해서는 충분히 높아야 한다. 그러나 신호를 샘플링 하는 과정에서 샘플링 주파수의 역수에 비례하는 이산화 오차가 발생하며, 이는 위치추정 결과에 오차를 유발하는 원인이 된다. 이산화 오차에 의한 도달시간차 방법의 위치추정 오차를 다음의 식으로 정리할 수 있다.
여기서 는 마이크로폰 배열에서 발생할 수 있는 최대시간차이를 나타내며, 두 마이크로폰 배열 축 방향과 나란하게 음파가 입사되는 경우에 해당한다. 은 샘플링 주파수의 역수에 해당하는 시간 분해능이고, n과 m은 각각 실제 시간지연의 정수 및 소수값을 나타낸다. Eq. (13)를 통해, 도달시간차 계산에 의한 위치추정 오차는 음파의 입사방향 및 이산화 오차에 의해 결정 될 수 있음을 알 수 있다.
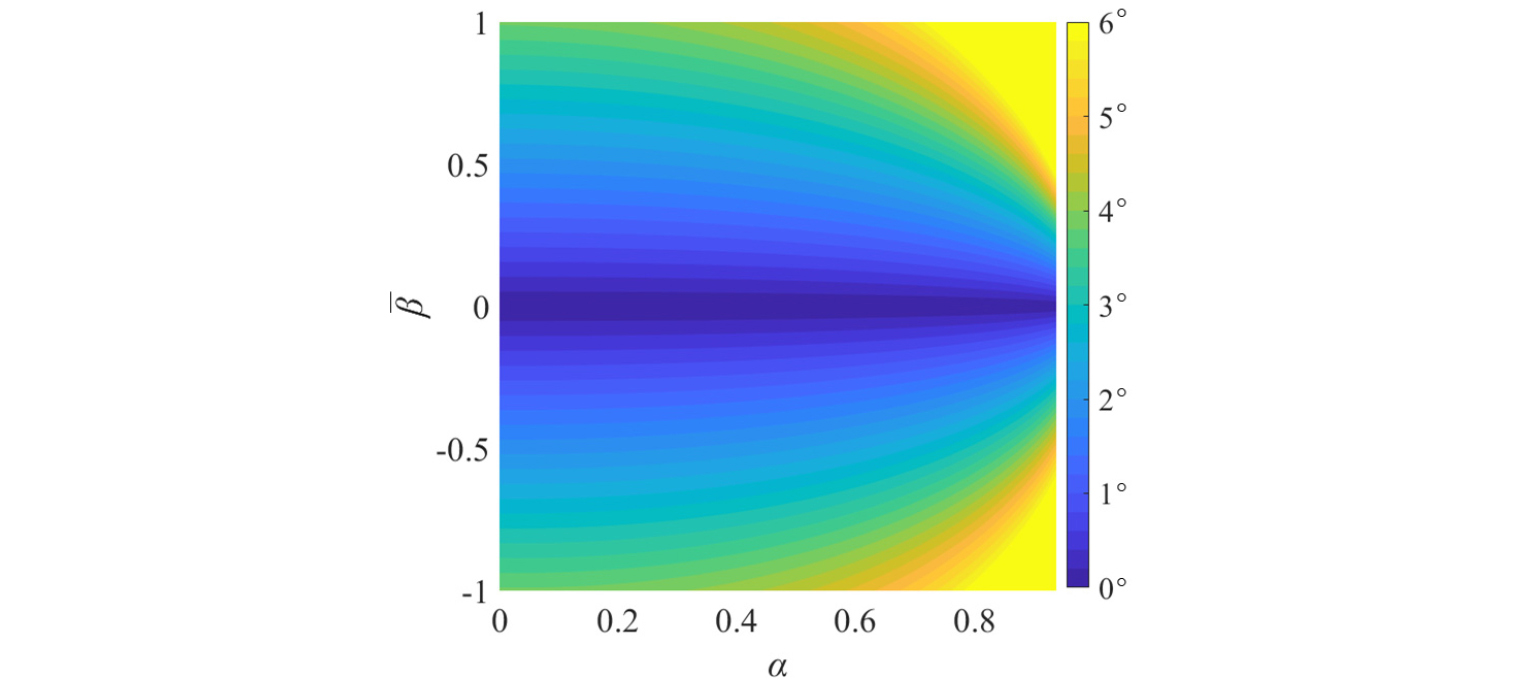
샘플링 주파수 및 음원의 입사방향이 위치추정 결과에 미치는 영향성을 분석하기 위해 다음과 같은 무차원 파라미터를 정의하였다.
| $$\alpha\equiv\frac{n\tau'}{\tau_{max}}=\frac{nc}{f_sd}=\frac{l_d}d,$$ | (14) |
| $$\beta\equiv\frac{m\tau'}{\tau_{max}}=\frac{mc}{f_sd}=\frac{l_\epsilon}d,$$ | (15) |
여기서 는 샘플링 주파수를 나타내고, 는 이산화 된 시간지연과 음속의 곱, 그리고 는 이산화에 의해 발생되는 오차를 나타낸다. 평면파가 입사되는 방향에 따라 두 마이크로폰을 통과하는 음파의 투영거리가 결정되며, 따라서 는 마이크로폰 간격에 대한 음파 투영 거리의 비, 그리고 는 이산화 오차 계수를 의미한다. Eqs. (13) ~ (15)을 토대로 도달시간차 계산을 통한 위치추정 오차를 , 에 관한 식으로 정리하면 다음과 같다.
| $$\epsilon_T=\sin^{-1}(\alpha\sqrt{1-(\alpha+\beta)^2}-(\alpha+\beta)\sqrt{1-\alpha^2}).$$ | (16) |
Fig. 2 에 d = 0.1 m, fs = 25.6 kHz, c = 343 m/s일 때 , 에 따른 위치추정 오차의 절댓값을 나타내었다. 여기서 는 의 최댓값으로 정규화하여 의 범위를 갖는 이산화 오차를 나타낸다. 인 경우는 마이크로폰 배열 축과 수직한 방향으로 음파가 입사 되어 두 마이크로폰 사이의 시간지연이 없는 조건이며, 은 최대 시간지연을 갖는 조건을 의미한다. 는 이산화 오차의 크기에 비례하며, 가 ±1에 가까워질수록 이산화오차가 큰 것을 의미한다. 따라서 음파의 투영 거리가 멀고, 이산화 오차의 크기가 클수록 위치 추정 오차가 커지는 것을 알 수 있다.
IV. 헬름홀츠 수에 따른 위치추정 오차의 비교
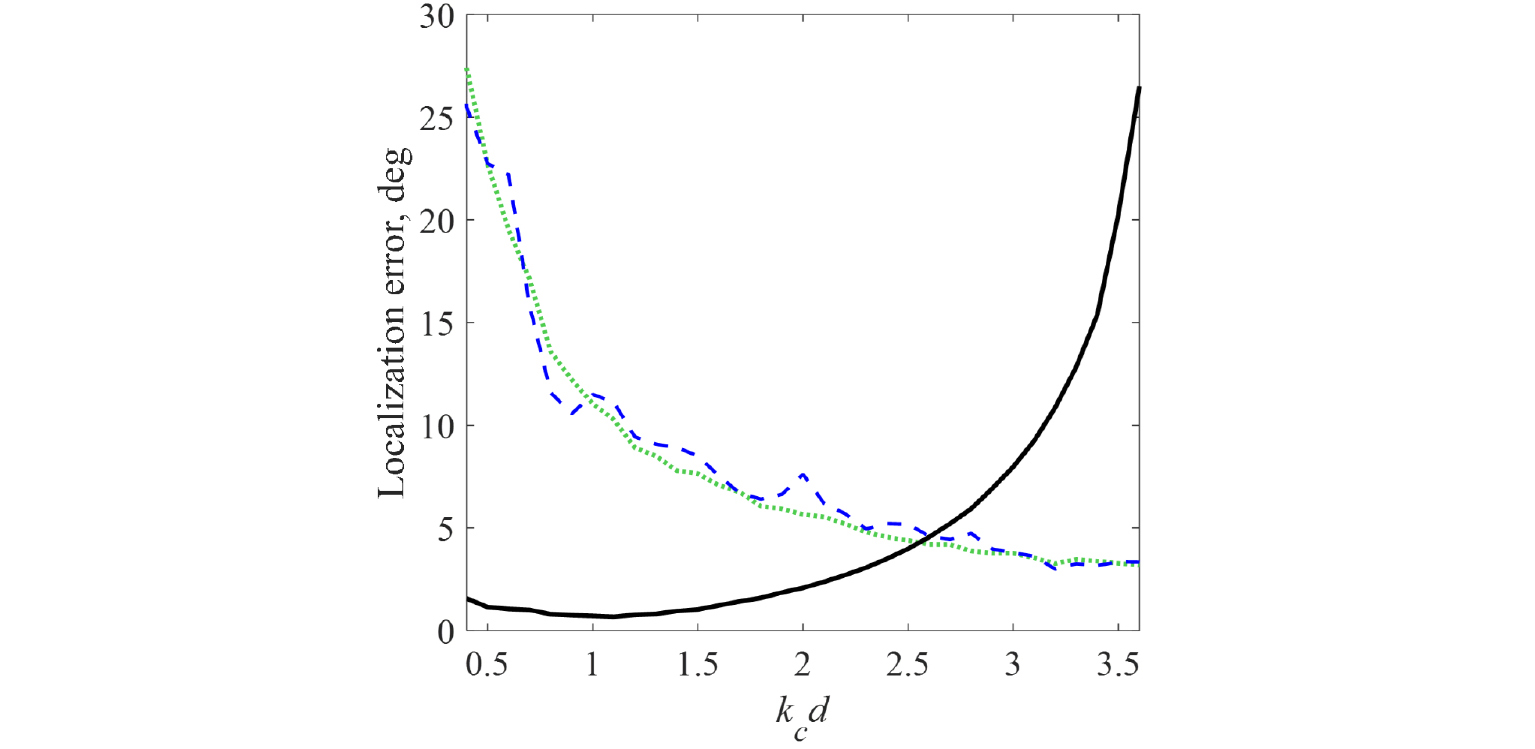
본 장에서는 Fig. 1과 같이 정사면체 형태의 3차원 마이크로폰 배열을 이용하여 도달시간차, 지연-합 빔포밍, 및 음향 인텐시티 벡터를 통한 위치추정 결과를 분석하며, 마이크로폰 간격을 변화시켜 헬름홀츠 수에 대한 위치추정 결과를 비교한다. 이와 관련한 선행연구에서는 3개의 마이크로폰으로 구성된 평면 배열을 통해 오직 방위각에 대한 위치추정 오차 비교를 수행하였으나,[17] 본 연구에서는 3차원으로 입사되는 음원에 대하여 높은 해상도로 고도각 및 방위각에 대한 위치추정 오차를 비교하였다.
음장 내 산란 및 반사가 없는 완전한 자유음장조건에서, 신호 대 잡음비는 70 dB이며 1.7 kHz에서 2.2 kHz의 대역 제한 백색잡음 신호를 갖는 평면파가 입사되는 조건에서 마이크로폰 간격을 d = 14 mm에서 110 mm로 변경하여 헬름홀츠 수 kcd를 결정하였다. 여기서 kc 는 신호 대역의 중심주파수인 2 kHz에 해당하는 파수이며, 헬름홀츠 수의 해상도는 0.1이다. 평면파는 –90° ≤ ϕ ≤ 90°, -90° ≤ θ ≤ 90° 방향에서 10° 간격으로 입사되는 경우를 고려하였으며, 따라서 총 361개의 방향에 대한 위치추정 값을 공간 평균하여 비교한 결과를 Fig. 3에 나타내었다. 여기서 위치추정 오차는 음원의 실제 입사 방향과 추정된 방향 벡터의 사잇각으로 정의하였다.
위 실험 결과로부터, kcd = 2.6 기준으로 특성이 구별되는 것을 관찰할 수 있다. 즉, 1.7 kHz에서 2.2 kHz에 대한 대역 제한 백색잡음에 대한 위치추정을 수행할 때 d = 71 mm보다 작은 마이크로폰 간격을 가지는 경우에는 음향 인텐시티 법을 적용하였을 때 5° 미만의 평균 오차를 가지는 반면, 마이크로폰 간격이 그보다 커지는 경우에는 도달시간차 또는 빔포밍을 적용하였을 때 평균 오차가 감소하는 것을 볼 수 있다. 한편, kcd < 1인 경우에 음향 인텐시티 법을 통한 위치추정 시 오차가 약 1° 커지는 것을 볼 수 있으며, 이는 저주파수 대역에서 위상부정합에 의한 오차가 커지기 때문이다.[12] 또한 빔포밍에 의한 위치추정 오차는 도달시간차 계산을 통한 방법과 비슷한 경향성을 나타내었다. 이는 낮은 헬름홀츠 수에 대하여, 빔폭이 넓어져서 위치 추정의 정밀도가 크게 낮아지며, 센서 간격 및 샘플링 주파수에 따른 공간분해능이 떨어지기 때문이다.
Fig. 4 에 kcd가 1.0, 2.6, 3.0인 경우 고도각-방위각 공간상에 위치추정 오차를 나타내었다. 헬름홀츠 수에 따른 위치추정 오차 발생 경향성이 Fig. 3과 동일하게 관찰되며, 특히 음향 인텐시티 벡터를 이용한 위치추정 결과에서는 헬름홀츠 수가 증가함에 따라 특정한 방향에서 공간편향오차가 크게 발생하는 것을 관찰할 수 있다. 이러한 지향성은 마이크로폰 배열의 지향지수에 의해 결정된다.[16],[17],[18] 위의 결과를 통해서 음향 인텐시티 법은 낮은 헬름홀츠 수에서 위치추정 정확도가 높은 것을 볼 수 있다. 따라서 중-저주파수 대역의 소음을 발생하는 기계시스템에 대한 음원 위치 추정을 수행할 때 음향 인텐시티 벡터를 통한 음원위치추정 방법은 소형의 마이크로폰 배열로도 정확도를 향상시킬 수 있으며, 공간효율성이 높은 방법임을 알 수 있다.
V. 음원 위치추정 실험결과 비교
본 장에서는 정사면체 형태의 마이크로폰 배열을 모사하여 음향 인텐시티벡터 계산 및 GCC-PHAT[3] 알고리즘을 통해 임의의 방향에서 발생하는 음원에 대하여 위치추정 시뮬레이션을 수행한 결과를 비교하고, 마이크로폰 사이의 간격 변화에 따른 결과를 분석한다. 또한 잔향음장 내에서 실험을 수행한 결과를 비교한다.
5.1 마이크로폰 간격에 따른 위치추정 실험
자유음장조건에서 전파되는 평면파를 수치적으로 모사하여, 이에 대한 위치를 추정하는 시뮬레이션을 수행하였다. 여기서 평면파는 70 dB, 30 dB의 신호 대 잡음비를 갖는 대역 제한 백색잡음 신호이다. 수음점 사이의 간격 변화 이외의 변인을 통제하기 위해서 음장 내 산란 및 반사의 효과 등이 없는 완전한 자유음장조건을 만족하도록 하였다. 이에 따라 인텐시티 벡터 계산 시 발생하는 주파수편향오차는 무시하였다. 모사되는 마이크로폰 배열은 Fig. 1과 동일한 정사면체 형태이며, 수음점의 간격 d = 30 mm, 80 mm인 두 가지의 형태의 배열에 대해 실험을 수행하였으며, 이에 해당하는 헬름홀츠 수 kcd = 1.1, 2.9이다. 여기서 kc는 대역의 중심 주파수에 해당하는 파수이다. 샘플링 주파수는 25.6 kHz이며 200 ms 동안 샘플링 된 신호는 Hanning window를 통해 가중되었으며 평균은 수행하지 않았다. 음파가 입사되는 방향은 배열 구조의 대칭성을 고려하여 ≤ 60°, ≤ 60°로 제한하였다.
임의의 방향으로부터 입사되는 단일 평면파에 대하여 실험을 수행하였으며, 총 50개의 방향에 대한 결과를 통계적으로 분석하였다. 위치추정 결과는 음원과 동일한 주파수 대역 내의 값을 평균하여 계산하였다. 음향 인텐시티, GCC-PHAT 방법을 적용하였을 때 음원의 실제 입사 방향과 추정된 방향 벡터의 사잇각 오차의 평균 및 표준편차 를 Tables 1과 2에 나타내었으며, 신호 대 잡음비가 70 dB일 때 방위각 및 고도각에 대한 위치추정 오차 , 를 Fig. 5에 나타내었다. 각각의 마커는 하나의 평면파에 대하여 나타낸 위치추정 오차에 해당한다. 마이크로폰 간격 d = 30 mm인 경우, 인텐시티 벡터를 이용한 방법은 오차의 평균 1.1°, 표준편차 0.5° 미만으로써 GCC-PHAT에 비해 정확도 및 정밀도가 높은 것을 볼 수 있다. 이는 마이크로폰 사이의 간격이 좁아짐에 따라 유한차분오차가 감소하며, 공간편향오차가 작기 때문에 나타난 결과이다. 반면에 GCC-PHAT는 샘플링 주파수에 비해 마이크로폰 간격이 좁아짐에 따라 공간분해능이 낮아지며, 결과적으로 위치추정 오차가 크게 발생하였다. 이러한 마이크로폰 간격에 의한 특징은 d = 80 mm인 실험결과에서 상반되어 나타난다. GCC-PHAT를 통한 위치추정 오차의 평균은 3.7° 미만인 반면, 인텐시티 벡터를 이용한 방법에서는 7.6° 미만의 오차를 나타낸다. 신호 대 잡음비가 낮은 경우에는, 오차가 증가하지만 증가폭이 1.5° 미만인 것을 관찰할 수 있다. 마이크로폰 간격에 대한 특성은 Fig. 3에서도 관찰할 수 있으며, kcd = 1.1, 2.9인 경우와 상응한다. 본 실험결과를 통해 인텐시티 벡터를 이용한 위치추정 방법은 수음점 사이의 간격이 좁을수록 위치추정 정확도 및 정밀도가 높은 반면, GCC-PHAT는 수음점 사이의 간격에 대해 상반된 특징을 갖는 것을 볼 수 있다.
Table 1. Comparison of the localization error for acoustic intensity, GCC-PHAT method when the microphone spacing d = 30 mm.
| Intensity vector | GCC-PHAT | |||
| SNR | 70 dB | 30 dB | 70 dB | 30 dB |
| 6.9° | 7.6° | 3.1° | 3.7° | |
| 2.9° | 2.7° | 1.5° | 2.1° | |
Table 2. Comparison of the localization error for acoustic intensity, GCC-PHAT method when the microphone spacing d = 80 mm.
| Intensity vector | GCC-PHAT | |||
| SNR | 70 dB | 30 dB | 70 dB | 30 dB |
| 6.9° | 7.6° | 3.1° | 3.7° | |
| 2.9° | 2.7° | 1.5° | 2.1° | |
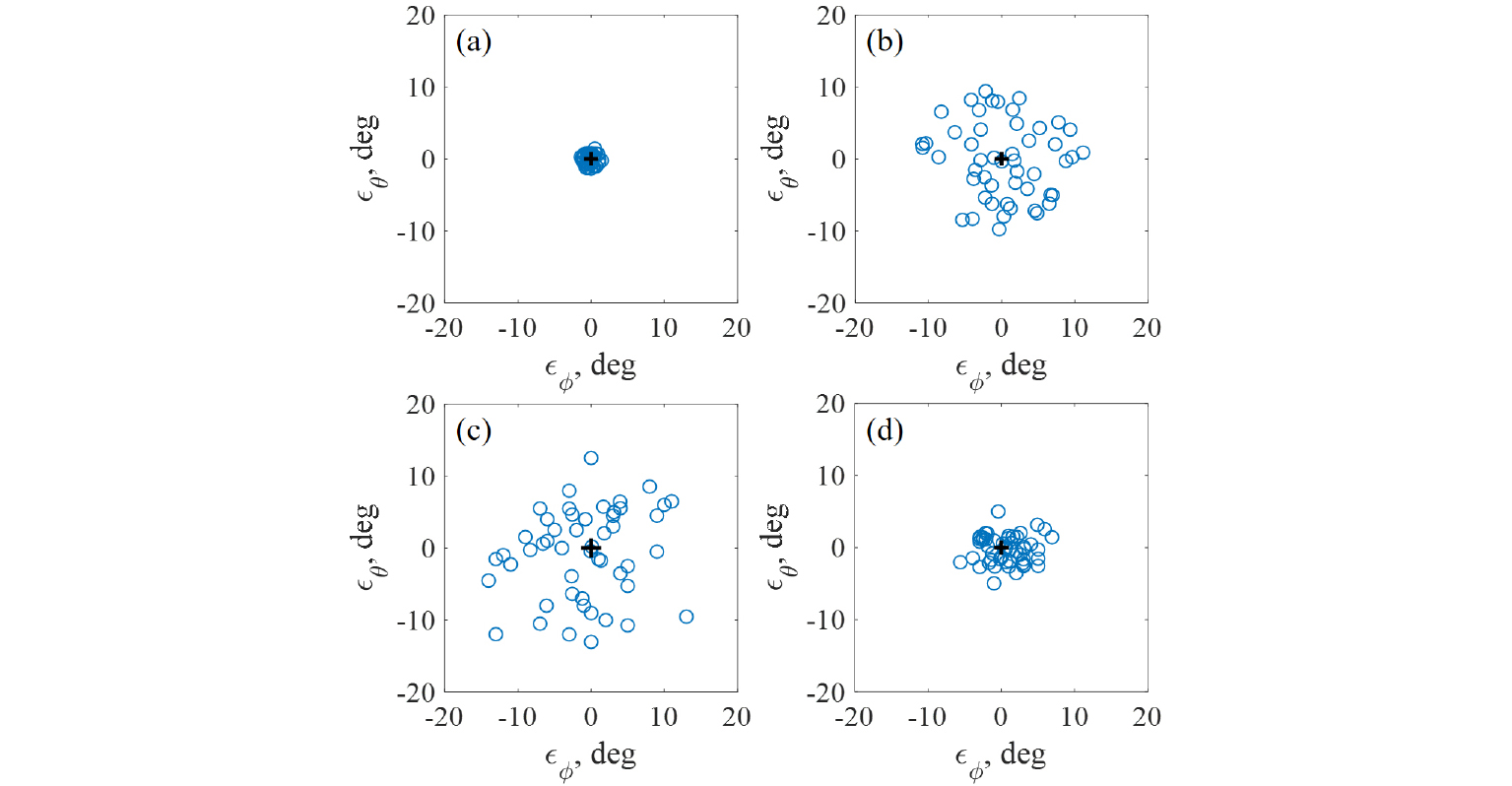
Fig. 5.
Localization error for a plane wave source having 70 dB SNR in the free field using a tetrahedral probe with varying spacing between microphone spacing d. The different localization methods are adopted: (a), (b) 3D acoustic intensity, (c), (d) GCC-PHAT. (a), (c) d = 30 mm, (b), (d) d = 80 mm.
5.2 잔향음장 내 위치추정 실험
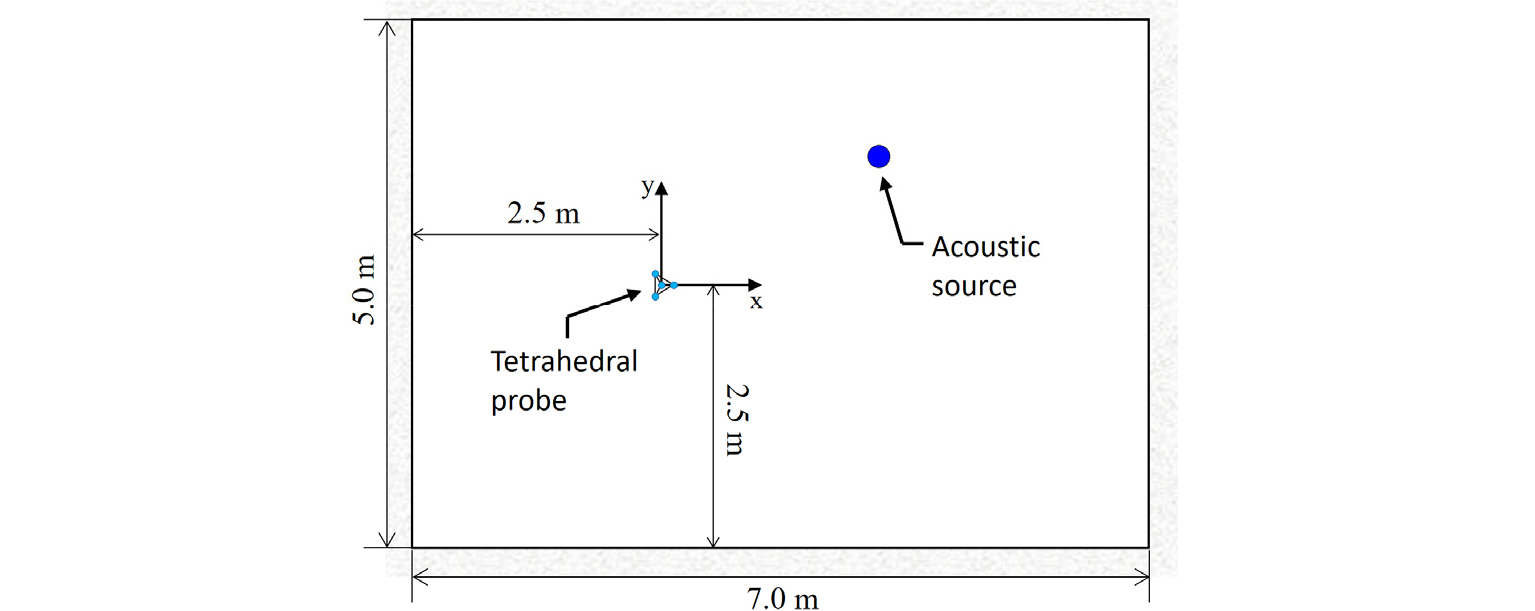
실제 실험환경은 대부분 자유음장이 아니므로, 음향 인텐시티 벡터를 이용한 음원위치 추정 방법의 실질적인 유효성을 검증하기 위해 image-source 법[21] 을 통해 잔향음장에서 음원위치추정 실험을 수행하였다. 실험공간은 5.0 m × 7.0 m × 2.5 m의 직육면체 형태이며 각 면의 흡음계수는 동일하게 설정하였고, Sabine의 공식에 따라 결정된 잔향시간 T60 = 0.4 s, 0.6 s, 0.8 s, 1.0 s인 조건에서 실험결과를 비교한다. 실험환경 및 시스템 구성을 Fig. 6에 나타내었다. 마이크로폰 배열은 정사면체 형태이며, 수음점의 간격이 d = 30 mm, 80 mm인 두 종류의 배열을 사용한다. 배열의 음향중심은 측면과 2.5 m 떨어져있으며, 바닥면과 1.25 m 떨어져 있다. 음원은 0.5 kHz에서 3.7 kHz의 대역 제한 백색잡음을 발생하고, d = 30 mm 및 d = 80 mm에 대한 헬름홀츠 수의 범위는 각각 0.3 < kd < 2.0, 0.7 < kd < 5.4이다. 음원과 배열의 음향중심 간의 거리는 1 m 이상이며, 음장 내 임의의 위치에 배치하였다. 데이터의 계측 시간은 1 s이며, 이외의 샘플링 조건은 5.1절과 동일하다. 본 실험에서는 음향 인텐시티 및 잔향음장에서 정확도가 높은 방법으로 알려진 GCC-PHAT를 적용하여 T60에 대한 실험결과를 각각 비교하였으며, 음향 인텐시티 벡터 계산 시 발생하는 편향오차를 보상하기 위해 절단된 상호상관함수를 적용하였다.[16] 위치추정 오차는 음향중심을 기준으로 음원의 실제 방향벡터 및 추정된 방향벡터 간의 사잇각으로 정의한다.
Fig. 7은 동일한 실험 공간 내 임의의 50개 지점에 대한 음원위치추정 오차에 대한 분포를 나타낸다. d = 30 mm이고 T60 = 0.4 s인 경우, 음향 인텐시티를 적용한 결과에서는 평균 오차가 2.9°이며 GCC-PHAT를 적용한 결과에서는 7.3°의 평균오차를 가지는 것을 볼 수 있다. T60가 증가함에 따라 평균오차 및 편차가 커지며, T60 = 1.0 s인 경우 음향 인텐시티는 9.9°, GCC-PHAT은 13.0°의 평균 오차를 가지는 것을 볼 수 있다. 반면 d = 80 mm인 경우, T60 = 0.4 s, 1.0 s일 때 음향 인텐시티를 적용한 결과에서 평균 오차는 각각 5.5°, 13.0°이며 GCC-PHAT를 적용한 결과에서는 각각 5.0°, 10.8°의 평균오차를 가지는 것을 볼 수 있다. T60가 증가함에 따라 오차의 평균 및 편차가 커지지만, d = 80 mm인 경우에는 GCC-PHAT 가 더 정확한 결과를 나타내는 것을 볼 수 있다. 음향 인텐시티를 통한 음원위치추정은 T60가 커짐에 따라 오차의 범위가 넓어지는 것을 관찰할 수 있으며, 따라서 반사음이 위치추정에 미치는 영향성이 상대적으로 큰 것을 알 수 있다. 그러나 마이크로폰 사이의 간격이 좁은 경우에는 GCC-PHAT에 비해 평균 오차가 작고, 이상 값(outlier)의 발생 빈도가 낮은 점을 통해 잔향음이 고려되는 실제 실험환경에서도 음향 인텐시티 벡터 계산을 통한 음원위치 추정 방법을 적용할 수 있음을 알 수 있다.
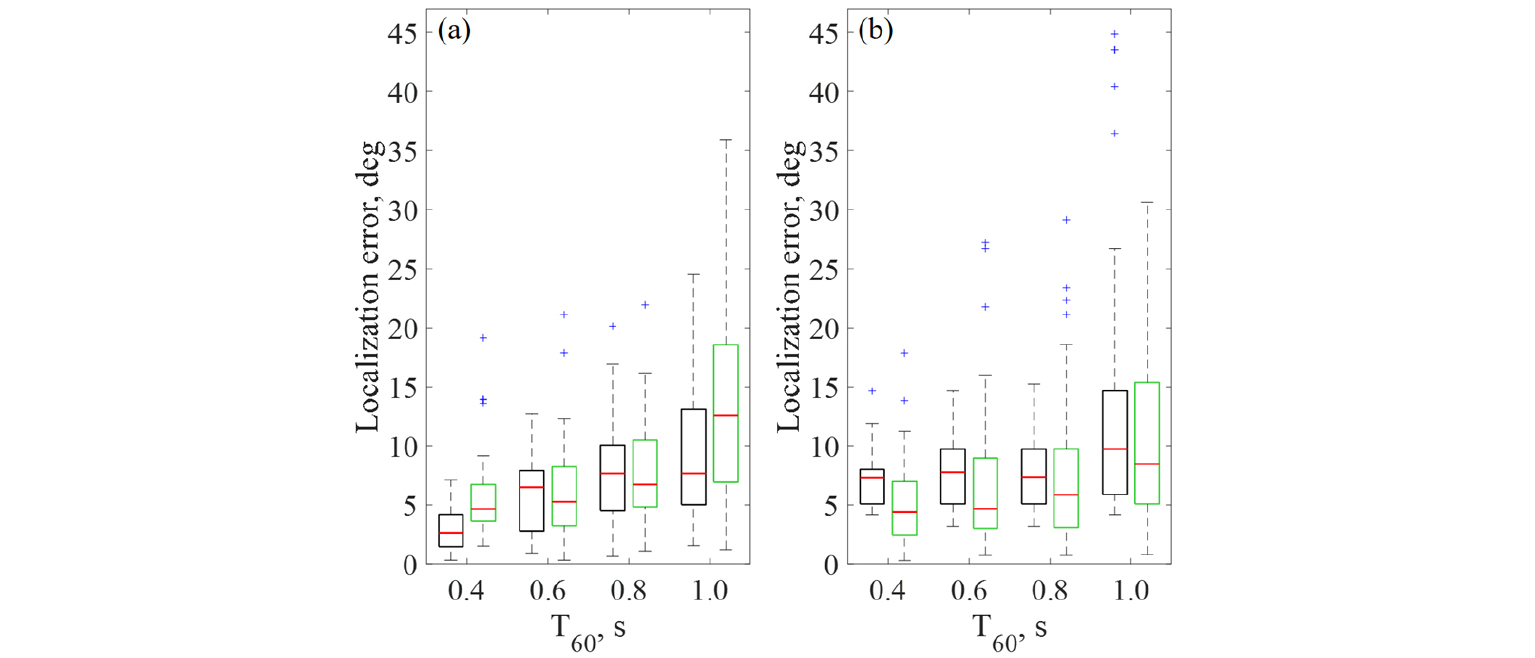
Fig. 7.
Localization error of source localization in the reverberant field using a tetrahedral probe for varying T60. (a) 3D acoustic intensity w/truncated cross- correlation,[16] (b) GCC-PHAT. The meaning of symbols: , median; , error range; , 1th-3th quartile of d = 30 mm; , 1th-3th quartile of d = 80 mm; , outlier.
VI. 결 론
본 논문에서는 음향 인텐시티 벡터 및 음파 도달시간차 계산을 통한 음원위치추정 방법 및 이때 발생되는 오차에 대해 설명 하고, 헬름홀츠 수에 대한 위치추정 결과를 비교하였다. 정사면체 형태로 배열된 마이크로폰을 이용한 위치추정 실험을 통해 음향 인텐시티 벡터를 이용한 방법이 음파 도달시간차 계산 방법에 비해서 헬름홀츠 수가 낮을수록 위치추정 정확도 및 정밀도가 높은 것을 확인하였다. 또한 동일한 마이크로폰 배열을 이용하여 잔향음장에서 음원 위치추정 실험을 수행한 결과, 음향 인텐시티 벡터를 계산한 결과에서는 잔향시간이 길어질수록 평균오차 및 편차가 커지지만 GCC-PHAT를 적용한 결과에 비해 평균 오차가 작은 것을 관찰할 수 있었다. 결론적으로, 매우 심한 반사를 제외한 일반 잔향장이 고려되는 실제 적용 환경에서도 음향 인텐시티법은 음원의 위치를 추정하는데 매우 작은 오차를 가지고 적용될 수 있는 것을 알 수 있고, 이에 따라 다양한 적용 가능성을 지니는 소형 마이크로폰 배열에 적합한 방법임을 알 수 있다.



 , TDoA method;
, TDoA method;  , beamforming method;
, beamforming method;  , acoustic intensity method.
, acoustic intensity method.