I. 서 론

연안에는 선상 수‧출입 물자의 출입을 위한 항이나, 발전소, 석유‧가스 매장지 등의 기반 시설이 위치하고 있다. 중요 기반 시설이 많은 연안을 보호하기 위하여 연안에서의 소나를 이용한 연안 탐지는 필수적이다. 함정 등 대형 표적은 자체 방사 소음을 탐지하는 수동소나로 탐지가 가능하나, 소형 표적은 자체 방사소음이 작아 수동탐지로는 탐지가 어렵다. 그러므로 소형 표적 탐지에는 능동 핑을 송신하여 반향되어 나오는 신호를 이용하는 능동소나가 적합하다. 저주파 능동소나는 고주파 능동소나에 비하여 음파 도달 거리가 길다는 장점이 있으나, 거리 해상도가 높지 않아 소형 표적의 탐지에는 적합하지 않다. 그러므로 소형 표적 탐지에는 고주파의 능동 펄스를 송신하는 고주파 능동소나가 사용된다.^[1] 고주파 능동소나는 짧은 음파 도달 거리를 단점으로 가지나, 연안 환경에서 소형표적 탐지는 적용 위치가 연안의 항구와 같은 비교적 좁은 영역이므로 긴 음파 도달거리는 요구되지 않는다.^[2]

연안 환경에서 소형 표적 탐지를 위한 신호처리 시스템 설계는 기 제안된 바 있다. Reference [2]에서는 고정된 고주파 능동소나 시스템에서 능동 펄스의 송신 후 수신 신호를 처리하여 규준화 하는 과정까지는 상세하게 기술되어 있으나, 측정치는 규준화 후 신호에 대하여 문턱값 이상의 첨두치로 비교적 간단하게 추출한다. 그러나 고주파 능동소나의 경우 고주파의 광대역 펄스를 송신 신호로 채택함으로써 거리해상도가 매우 높아 변동(fluctuation)이 심하고 이에 따른 오경보가 많다. 또한 하나의 표적에 대하여 다수의 측정치가 추출되는 상황이 발생하며, 이 경우 측정치들을 하나로 표현할 필요가 있다.

본 논문에서는 연안 환경에서 고주파 능동소나를 이용한 소형 표적 탐지에 적합한 탐지 알고리듬을 제안한다. 제안하는 탐지 알고리듬은 문턱값 이상 신호 주변의 통계적 특징을 측정치 추출에 이용하는 Constant False Alarm Rate(CFAR)를 이용하여 오경보율을 낮추고,^[3] 하나의 표적으로부터 발생된 다수의 측정치를 클러스터링을 통하여 하나의 측정치로 도출함과 동시에 해양생물들의 과도신호에 의한 클러터를 제거한다.

본 논문의 구성은 다음과 같다. 서론에 이어 II에서는 연안 환경에서 소형 표적 탐지를 위한 고주파 능동소나 신호처리 시스템에 대하여 간략히 언급하고, III장에서는 탐지 알고리듬을 제안한다. IV장에서는 제안한 탐지 알고리듬의 성능을 해상시험을 통하여 검증하고, V장에서는 결론을 맺는다.

II. 연안 환경에서 소형 표적 탐지를 위한 고주파 능동소나 신호처리

소형 표적 탐지를 위한 고주파 능동소나는 송신 중심주파수가 고주파이므로 센서에서의 샘플링 주파수가 매우 높다. 데이터의 양은 샘플링 주파수와 비례하고, 이에 따른 과도한 연산량은 연산에서의 실시간성을 보장하지 못한다. 과도한 데이터량과 이에 따른 연산량을 줄이기 위하여 수신 센서신호를 송신 펄스 중심 주파수의 반송파 신호를 곱하여 기저대역으로 천이시키고, 저역통과필터를 거친 다음 간축을 수행한다. 소형 표적의 효과적인 탐지를 위하여 거리 해상도가 대역폭에 비례하는 Frequency Modulation(FM) 형태의 송신 펄스가 사용된다.^[4] 저역통과필터의 설계는 FM 펄스의 대역폭을 고려하여 설계되어야 한다. 저역통과필터를 통과시킨 신호를 이용하여 빔형성을 수행한다. 시간영역의 빔형성은 시간영역에서 센서신호를 지향각과 센서 배열에 따라 보간율을 정하여 보간을 수행하고, 창 함수를 곱한 신호의 지연-합으로 이루어진다. 이 때 보간으로 인한 데이터량 및 연산량의 증가로 실시간성이 보장되지 않을 수 있다. 빔형성의 기본 개념인 시간 영역에서의 지연-합이 주파수 영역에서 위상-합임을 이용하여, 주파수영역에서 빔형성을 수행하면 연산량을 감소시킬 수 있다.^{[2], [5]}

빔형성된 신호는 송신펄스와의 상호 상관을 수행하는 정합필터를 거친다. 만약 빔형성이 주파수 영역에서 수행되었다면, 시간영역에서 상호상관이 주파수 영역에서 빔형성 출력의 주파수 스펙트럼과 복제신호(replica)의 켤레 복소수와의 곱임을 이용하여 주파수 영역에서 수행 가능하다.^[6]

연안에서 소형 표적 탐지를 위한 소나는 선박의 출‧입항 등으로 인한 항구의 교통 복잡성으로 인하여, 센서가 이동형이기 보다는 고정형으로 설계된다. 센서가 고정될 경우 연안에 준설된 방파제와 같은 고정된 해저 지형물에 의한 고정 클러터가 매우 많이 발생하고, 이는 오경보율의 증가로 이어진다. 그러므로 선박 및 함정 등에 탑재된 이동형 소나에서 사용되는 스플릿-창 규준화(split-window normalization)는 고정된 센서를 사용하는 능동소나에 적합하지 않다. 왜냐하면 수신신호의 시간적 이전, 이후 값만을 이용하여 규준화를 수행하므로, 연안의 방파제와 같은 고정된 클러터가 지속적인 오경보로 발생하기 때문이다. 그러므로 고정형 능동 소나의 경우 주변 해저 지형 환경에 따른 잔향 신호를 추정하여 클러터 맵을 생성하여 고정된 클러터로 인한 오경보에 강인한 규준화 기법이 사용된다.^{[2], [7]}

III. 연안 환경에서 클러터에 강인한 능동소나 탐지 알고리듬

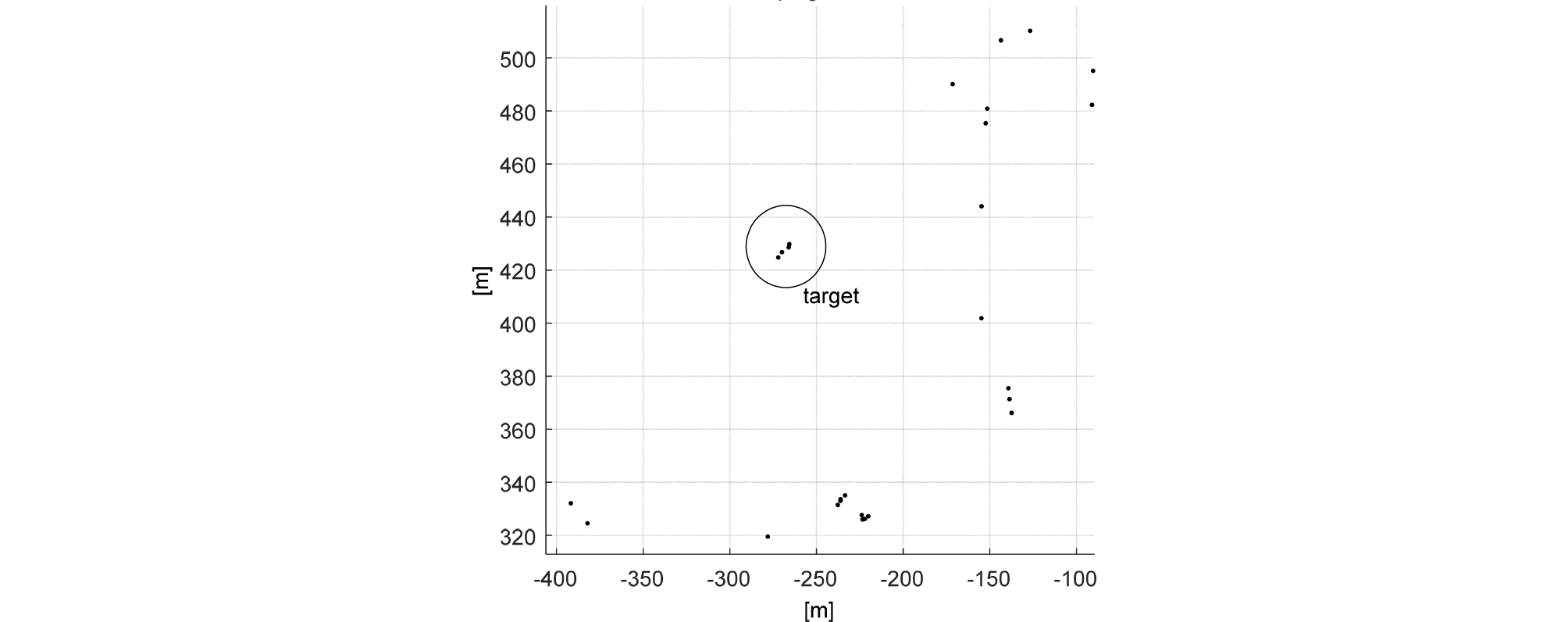
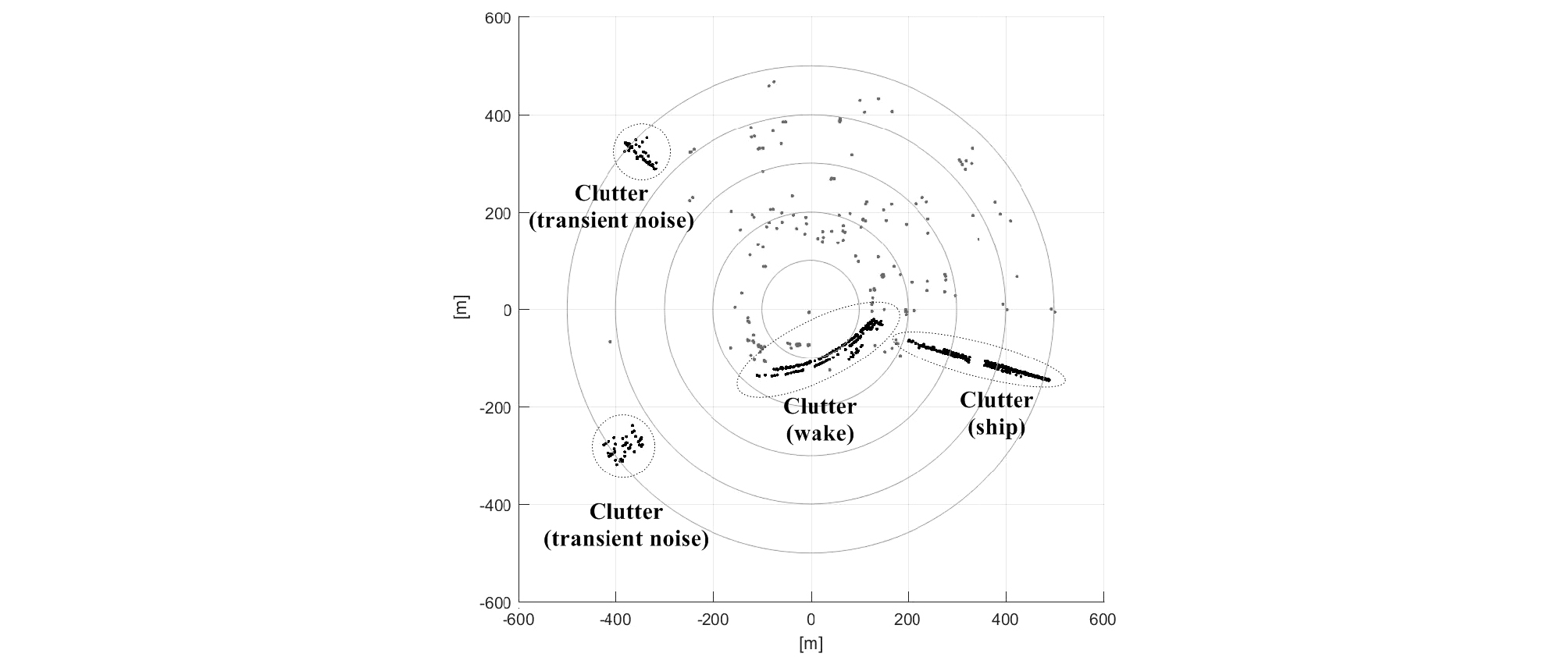
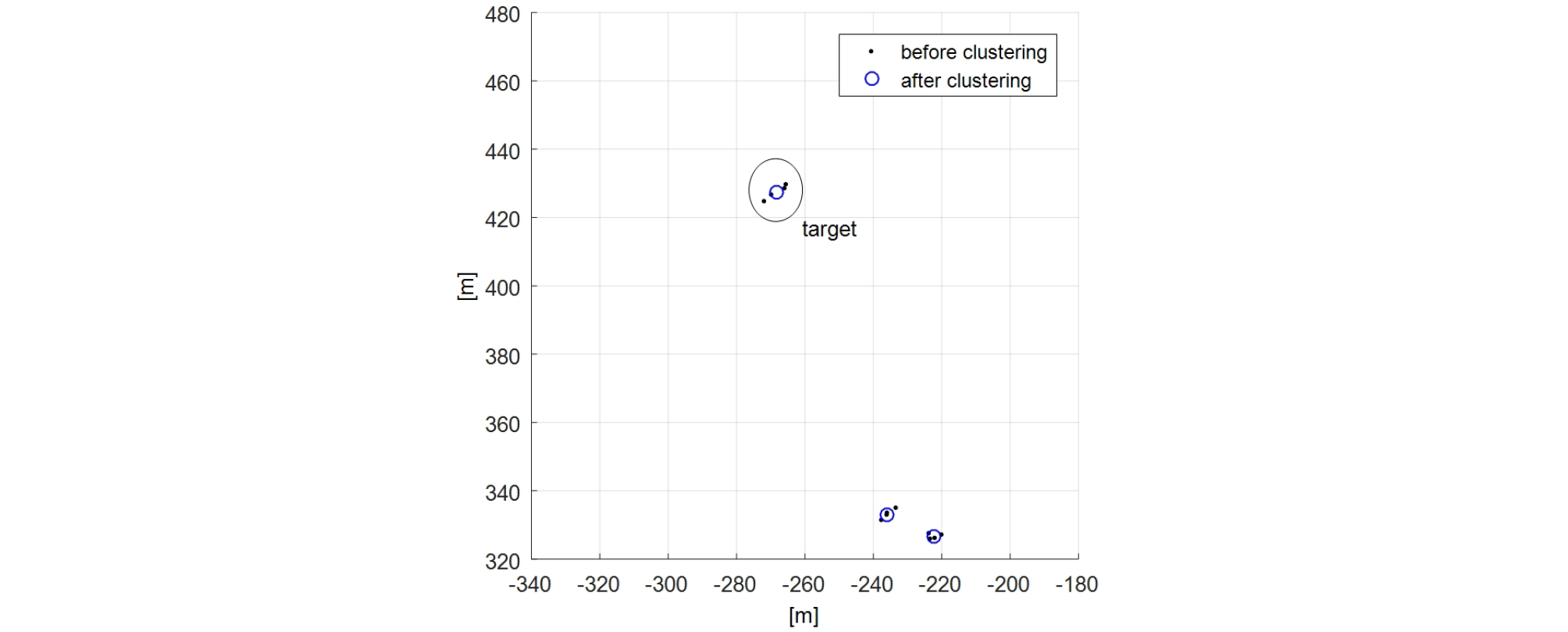
규준화 출력신호 중 설정한 문턱값 이상의 첨두치 신호는 측정치로 추출된다. 고주파 능동소나의 경우 샘플링 주파수가 높아 신호의 변동이 심하고, 개방형 호흡기를 착용한 다이버와 같은 소형표적의 경우 호흡이 이루는 공기방울에 의한 클러터로 인하여 Fig. 1과 같이 하나의 표적이 다수의 측정치로 나타난다. 또한 Fig. 2와 같이 해양생물 의한 과도 신호, 선박 소음, 항적에 의한 측정치는 심각한 오경보를 발생시킨다.

Fig. 1.

Multiple measurements from a target (diver with open circuit breather).

Fig. 2.

Measurements of clutters from transient noise, wake and ship noise.

본 논문에서는 표적신호의 통계적 특징을 이용하는 CFAR의 적용과 클러스터링을 통하여 하나의 표적에 의한 다수의 측정치를 하나로 표현하여 클러터를 제거하였다.

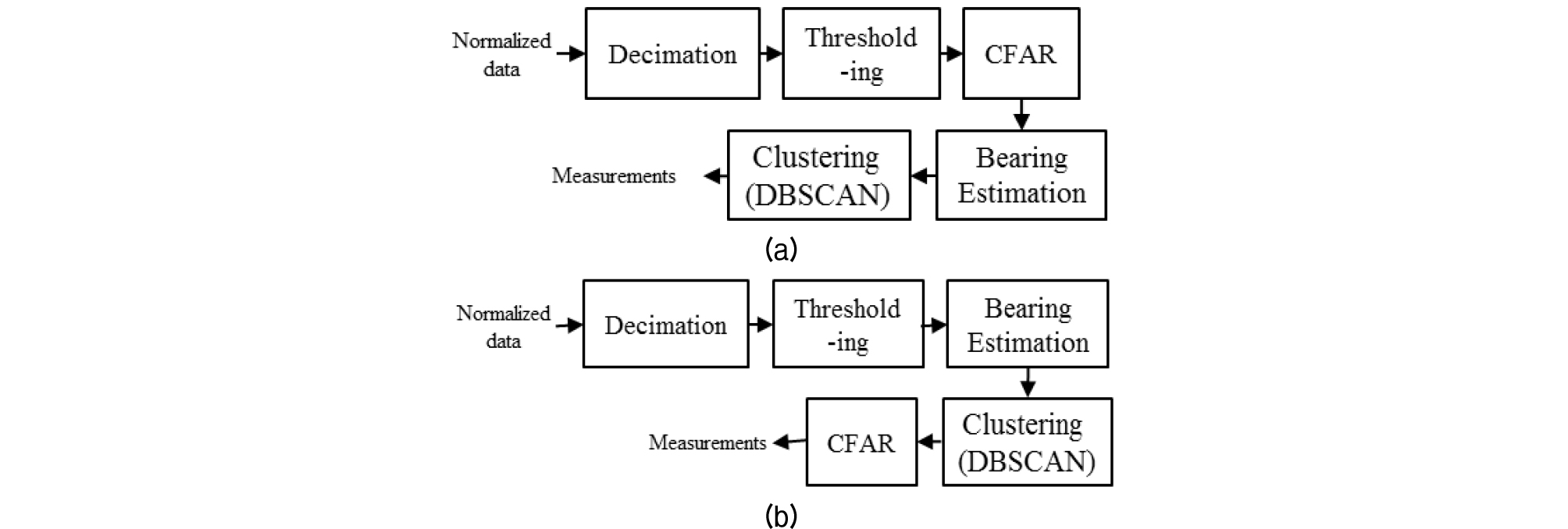
제안하는 알고리듬의 블록 다이어그램은 Fig. 3에 나타내었다. Fig. 3의 (a)와 (b)의 규준화 출력 신호는 $x(n,b)$로 나타낼 수 있다. $n$은 샘플 인덱스로 시간 $n{T}_S$을 나타내며, $T_S$는 규준화 데이터의 샘플링 주파수 이다. 형성된 빔의 수는 $N_b$개이며, $b$는 빔 인덱스로 신호의 지향각 $\theta \left(b\right)$이 $2\pi b/N_b$임을 나타낸다($b=0,1,...,N_b-1$).

Fig. 3.

Block diagrams of proposed algorithm (a) clustering after CFAR (b) CFAR after clustering.

고주파 능동소나의 경우 I장에서 언급한 것과 같이 샘플링 주파수가 높고, 신호처리 이득을 위하여 광대역의 송신 신호를 채택하며, 이는 높은 거리 해상도를 가진다. 높은 거리 해상도의 송신 신호에 의한 반향 신호는 신호 변동에 민감하므로 하나의 반사체로부터 다수의 측정치가 발생한다. 이의 영향을 감소시키기 위하여 간축을 수행한다. 간축비 $D$는 송신 FM 펄스의 대역폭을 $B$라 하고 음속을 $c$라 할 때, FM 모호함수의 정점에서 3 dB 감소되는 지점의 거리 해상도 $2B/c$와 탐지 대상 표적의 크기를 고려하여 결정하여야 한다.^[8] 본 논문에서는 간축은 일반적인 간축과 다르게 신호의 첨두값을 유지하기 위하여, 간축비 내 신호의 최대치를 선택하여 간축을 수행한다. 간축된 규준화 신호는 다음과 같이 나타낼 수 있다.

정확한 거리의 추출을 위하여 간축 시 신호의 간축 전 인덱스를 동시에 추출하며, 간축 전 인덱스 $l_D(k,b)$는 다음과 같이 나타낼 수 있다.

문턱값 $TH$ 이상인 $x_D(k,b)$ 중 방위, 거리 상 거리 상 첨두값 신호는 측정치 후보가 된다. 측정치 후보 집합 ${\mathbf{M}}_{Candidate}$은 다음 과 같이 나타낼 수 있다.

${\mathbf{M}}_{Candidate}$에 해당하는 측정치의 거리는 간축 전인 거리 인덱스인 $l_D(k,b)$에 음속 $c$를 곱하여 샘플링 주파수의 역수를 곱하고 2로 나눈 값이다.

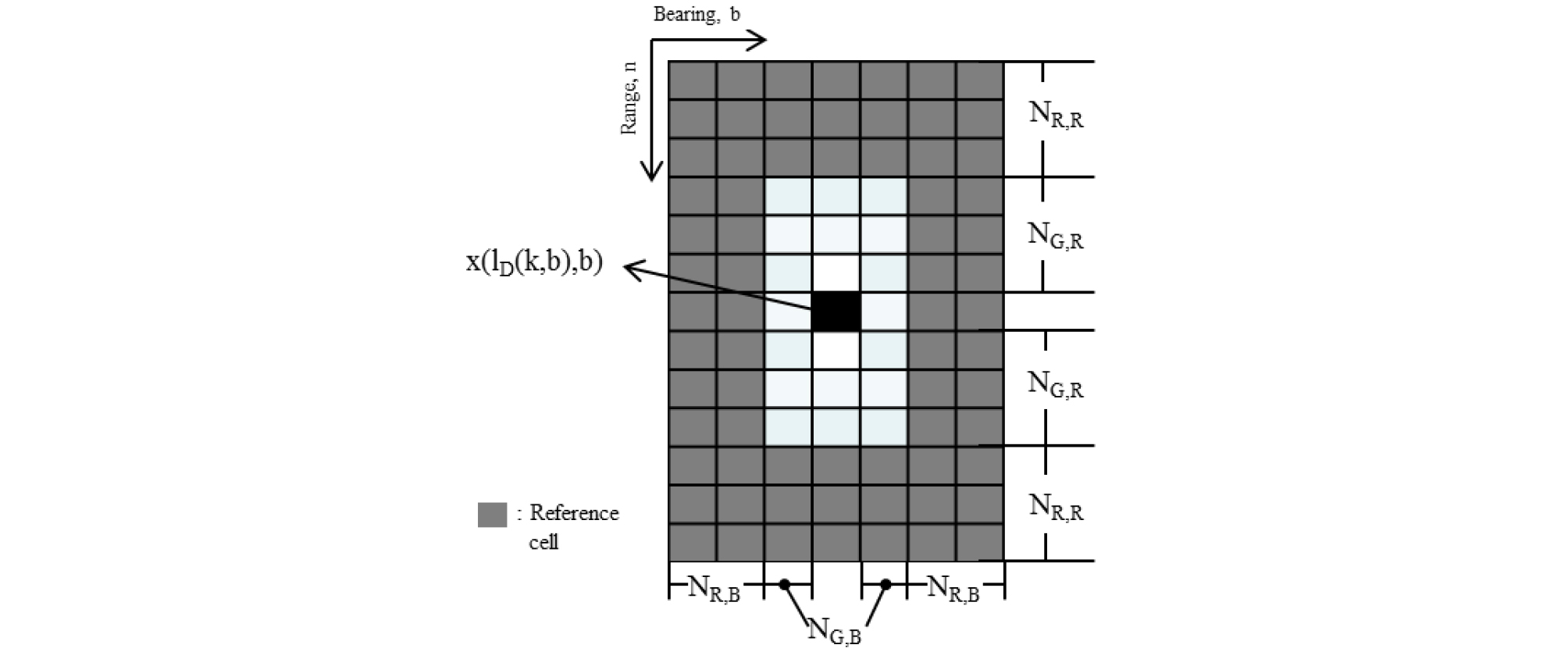
본 논문에서는 II장에서 고정된 송‧수신 센서 환경에 적합한 잔향 추정 기반의 클러터 맵을 이용한 규준화를 신호처리에 적용하였다. 이는 연속된 송신펄스 전송에서 잔향 환경이 짧은 시간 내에 변화하지 않아 고정된 환경에서의 반사 신호는 차이가 작을 것임에 바탕을 두었다. 그러나 이 방법은 연속된 송신 핑의 수신신호를 이용하여 규준화를 수행한 것이고, 하나의 송신 핑의 수신 신호 상에서 이웃 시간(이웃 공간)의 신호 환경을 이용하여 규준화한 것은 아니다. 예를 들어 딱새우와 같은 해양생물이 발생시키는 과도신호는 단일 핑에서 발생하고, 클러터 맵을 이용한 규준화 신호에서 문턱값 이상의 측정치를 추출할 경우 이전 핑에서 추정된 잔향환경과 다르므로 단일 핑 내에서 일정시간 지속되는 과도신호 모두 측정치로 발현된다. 본 논문에서는 클러터 맵을 이용한 규준화가 가지는 단점의 영향을 줄이기 위하 여 문턱치 이상의 첨두치의 간축 전 주변 신호의 통계적인 특성을 계산하여 비교하는 CFAR를 적용하여 최종 측정치를 결정한다.^[3] 간축 전 신호의 위치를 $\left(l_D\right(k,b),b)$라 하면 주변신호의 평균 $m\left(l_D\right(k,b),b)$과 표준편차 $\sigma \left(l_D\right(k,b),b)$를 구한다. 이 때 주변신호에서 표적신호를 배제하기 위하여, 보호 셀(guard cell)을 지정한다. $m\left(l_D\right(k,b),b)$와 $\sigma \left(l_D\right(k,b),b)$를 계산하기 위한 대상 신호의 집합은 아래와 같이 나타낼 수 있다.

여기서 $N_{R,B}$와 $N_{G,B}$는 방위 상 참조 셀과 보호 셀의 길이를 나타내고, $N_{R,R}$과 $N_{G,R}$는 거리상의 참조 셀과 보호 셀의 길이를 나타낸다. Fig. 4는 Eq. (4)를 그림으로 나타낸 것으로 회색음영으로 나타낸 부분이 $R\left(l_D\right(k,b),b)$에 해당하는 값이다.

Fig. 4.

Reference and guard area in calculation of characteristics of detected signal.

첨두치 신호가 변동이 심한 것을 감안하여, 주변 신호의 통계적 특성과 비교하기 전에 시간 상 이전‧이후 신호와 평균을 구한다. 이를 수식으로 표현하면 Eq. (5)와 같다.

최종 첨두치가 되는 조건은 아래 식을 만족하여야 한다.

Eq. (6)은 $x_{average}\left(l_D\right(k,b),b)$를 정규화 하였을 때, 정규화 한 값이 상수 $K$를 넘는다면, 이는 잔향신호와는 통계적 특성이 다른 측정치로 간주함을 의미한다. $K$ 가 높게 설정될수록 주변 값보다 크기가 큰 신호만 측정치로 추출되므로, 클러터 제거율은 높아지나 표적 탐지율은 낮아지는 특징이 있다.

방위는 Eq. (6)을 만족하는 신호 $x\left(l_D\right(k,b),b)$의 이전 지향각 신호 $x\left(l_D\right(k,b),b-1)$와 이후 방위 신호 $x\left(l_D\right(k,b),b+1)$을 이용한 이차 다항식 보간으로 추정하였다.^[9]

본 논문에서는 하나의 표적에서 여러 개의 측정치가 추출되는 현상에 의한 오경보를 줄이고, 해양생물 소음 및 선박 소음과 같은 과도 신호에 의한 군집된 클러터에 의한 오경보를 제거한다. 이를 위하여 측정치 간 거리에 기반한 클러스터링을 수행한다. 사용된 클러스터링 기법은 Density Based Spatial Clustering of Application with Noise(DBSCAN)이다.^[10] DBSCAN은 주어진 신호 간의 거리를 계산하고, 거리가 설정값 이하인 경우 이웃으로 선정한다. 이웃의 수가 정한 값 이상인 경우 코어 포인트로 지정한다. 코어 포인트가 다른 코어 포인트의 이웃이라면, 이웃인 코어 포인트와 그 이웃까지 하나의 클러스터에 속하게 된다. 이 때 클러스터를 형성하지 못한 측정치는 클러터로 간주되어 삭제된다. Fig. 5는 표적 측정치와 클러터의 클러스터링 결과를 보여주고 있다.

Fig. 5.

Cluster of target with sea trial data.

클러스터를 $C_i$라 표현하고, 총 클러스터의 수가 $N_{Cluster}$ 라 하면 클러스터 내 측정치는 $N_C\left(i\right)$라 둘 때 클러스터 $C_i$는 다음과 같이 나타낼 수 있다.

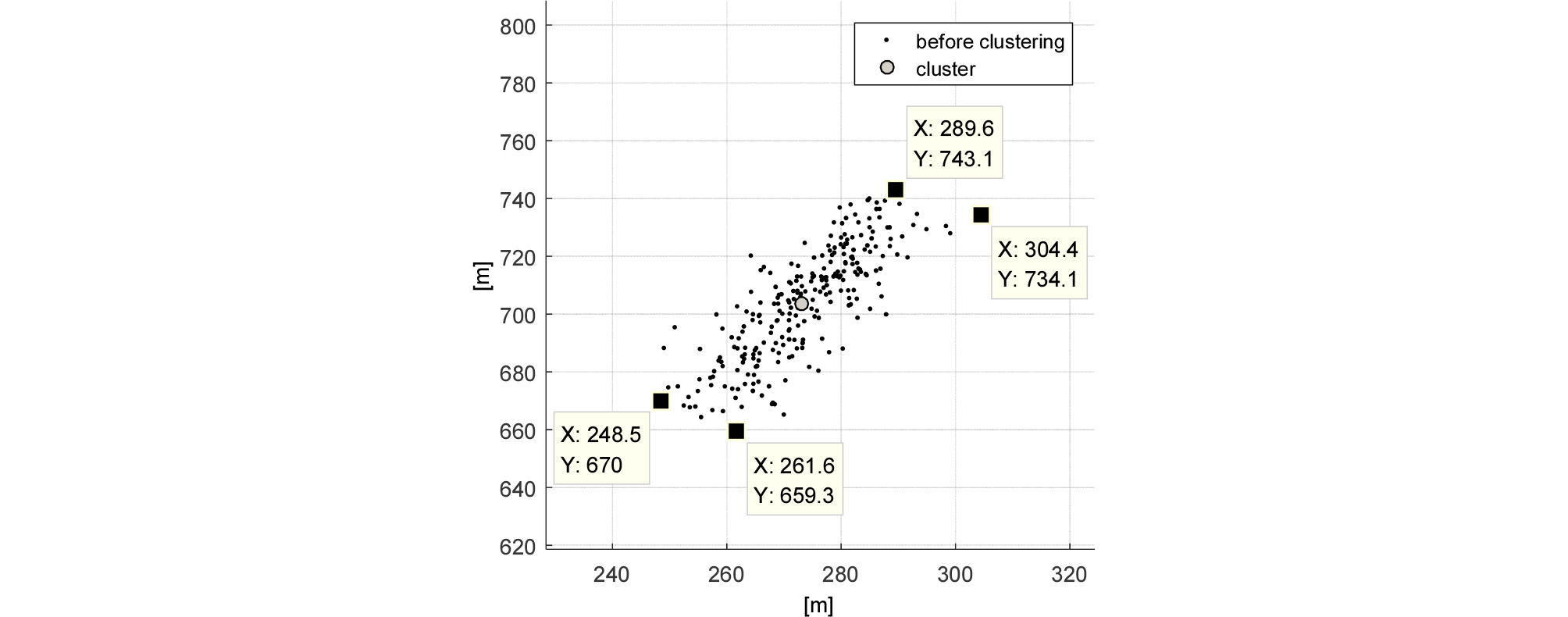
Fig. 2의 클러스터 중 수중 생물 또는 선박 소음에 의한 클러스터는 길이가 탐지 대상인 소형 표적의 클러스터 길이에 비하여 길다. Fig. 6은 과도신호로 구성된 클러스터이다. 클러스터의 길이는 클러스터 내 측정치의 수직, 수평 좌표의 최댓값과 최솟값의 차를 가로와 세로로 가지는 사각형의 대각선 길이로 정의할 수 있다. Fig. 6의 클러스터 길이는 48.7 m로 탐지하고자 하는 소형 표적의 길이라 볼 수 없다. 본 논문에서는 클러스터의 길이를 계산하여 기준치를 초과 시 제거하여 과도 신호와 선박 소음에 의한 오경보를 제한한다. 클러스터 $C_i$의 길이 $L_i$는 다음과 같이 정의한다.

Fig. 6.

Cluster consisted of measurements from transient noise.

계산된 클러스터 길이 $L_i$가 $L_{TH}$를 초과하는 경우 해당 클러스터를 제거한다. $L_{TH}$의 설정은 탐지하고자 하는 표적이 제거되지 않도록 표적의 크기와 그 오차를 고려하여 설정하거나, 실험과 분석을 통하여 설정하여야 한다.

표적에 의한 측정치가 Fig. 3의 (a)의 CFAR의 수행과정에서 Eq. (6)을 만족시키지 못하여 제거되면 클러스터 형성 조건(클러스터 내 측정치 수)을 만족시키기 못할 가능성이 있다. 본 논문에서는 표적 탐지 확률을 높이기 위하여 Fig. 3의 (b)와 같이 Eq. (3)의 측정치 후보를 입력으로 클러스터링을 하였다. 이후 형성된 클러스터 내에 CFAR를 적용하여 Eq. (6)을 만족하는 측정치가 있고, 클러스터 길이 $L_i$가 $L_{TH}$보다 작은 경우 이를 최종 측정치로 간주하였다. 이후 측정치의 위치는 클러스터 내 측정치의 수직좌표계상 위치에 정합필터 출력 크기를 가중치로 설정하여 계산하였다. 이는 클러스터 내 측정치의 정합필터 출력 크기를 $a_{N_C\left(i\right)}$, 클러스터 내 측정치의 정합필터 출력 크기 합을 $A_{C\left(i\right)}$라 할 때 클러스터의 위치 $(x_{C\left(i\right)},y_{C\left(i\right)})$는 다음의 식과 같이 나타낼 수 있다.

IV. 해상 실험 결과

본 장에서는 제안한 능동소나 탐지 알고리듬의 클러터 제거 성능을 해상실험 데이터를 이용하여 검증한다.

해상 실험 환경은 다음과 같다. 단상태 소나의 음원과 수신기는 동일한 위치에 고정 설치하였다. 사용된 송신 펄스는 길이가 200 ms, 대역폭 20 kHz인 Linear Frequency Modulation(LFM)펄스이다. 송신 펄스는 2 s 간격으로 100회 송신되었다. 시험 시 표적은 인양선에 의하여 센서로부터 500 m 떨어진 곳에서, 390 m 떨어진 곳까지 이동하였다.

본 논문에서 제안한 능동소나 탐지 알고리듬의 성능은 표적 탐지 확률과 클러터 제거율을 이용하여 검증하였다. Eq. (6)의 $K$는 2로 설정하였고, 클러스터의 길이 문턱값 $L_{TH}$는 40 m로 설정하였다. 또한 클러스터로 형성되는 최소 측정치 수는 2개로 설정하였다. 제안한 알고리듬의 검증에는 동일한 데이터를 이용하여 다섯 가지 측정치 추출 기법이 적용되었다. 첫 번째는 정합필터링 이후 고정된 문턱값 이상의 첨두치를 측정치로 추출하였고(Case 1), 두 번째는 신호의 통계적인 특성을 이용하는 CFAR의 클러터 제거 성능을 검증하기 위하여 첫 번째 측정치에 Eq. (6)과 같이 신호의 주변 신호 통계적 특성을 고려하여 측정치를 추출하였다(Case 2). 세 번째는 클러스터링의 성능을 분석하기 위하여 Case 2의 측정치를 클러스터링하여 대푯값을 산출하였다(Case 3). 네 번째는 첫 번째 방법의 측정치를 입력으로 클러스터링을 수행한 후 대푯값을 선정한 후 Eq. (6)의 측정치를 포함한 클러스터의 대푯값을 측정치로 추출하였다(Case 4). 다섯 번째는 네 번째 방법에서 과도신호에 의한 클러터 제거 성능과 $K$에 따른 클러터 제거 성능과 표적 탐지율을 확인하는 실험을 진행하였다(Case 5-1~6). 클러스터링 후 클러스터의 길이를 산출하고, 그 길이가 40 m 이상이면 제거하였다. 또한 $K$를 2에서부터 3까지 0.2 간격으로 설정하였다.

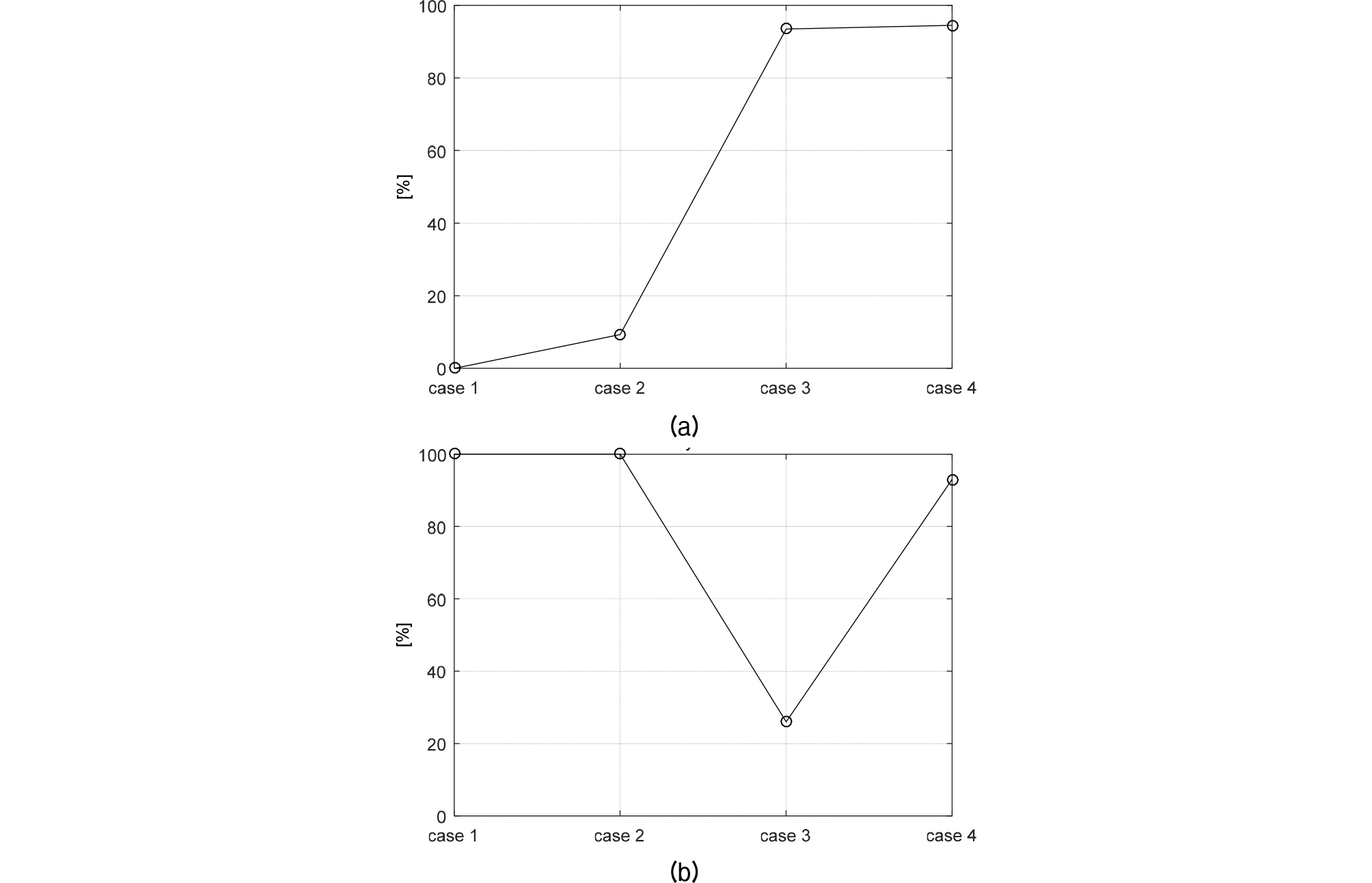
Case 별 클러터 제거율과 표적 탐지율은 Fig. 7의 (a)와 (b)에 나타내었다. 클러터 제거율은 Case 1의 클러터 수를 1로 설정하였을 때의 Case 별 클러터 수와의 비를 백분율로 나타낸 것이다. Case 1에 비하여 측정치 주변 신호의 통계적 특징을 반영한 Case 2에서 클러터가 9.32 % 더 제거되었다. Case 3, 4의 경우 클러스터링을 통한 클러터 제거율이 각각 93.47 %, 94.48 %이며, 이는 곧 오경보율의 감소를 의미한다. Case 3과 Case 4의 클러터 제거율의 차는 각 1.01 %로 크지 않으나, 표적 탐지율은 Case 3이 26 %로 Case 4에 비하여 67 % 적었다. 이는 Case 3에서 신호의 통계적인 특징을 이용한 클러터를 제거 시 표적 신호가 제거되어 표적신호가 클러스터로 형성되지 못하였기 때문이다. 이와 달리 Case 1과 2는 100번의 송신 핑에서 모두 표적이 탐지되었고, Case 4의 경우 표적 탐지율이 93 %였다. 일반적인 소나 시스템의 경우 탐지 이후 추적을 고려하므로 90 % 이상의 탐지율은 추적 알고리듬의 적용으로 보완 가능하다. 그러므로 클러터 제거율이 높아 오경보율이 낮고, 93 %의 표적 탐지율에 클러터 제거율이 가장 높은 Case 4가 연안 환경에서 소형표적 탐지 알고리듬으로 가장 적합함을 알 수 있다.

Fig. 7.

Clutter reduction rate and target detection rate according to five cases (a) clutter reduction rate and (b) target detection rate.

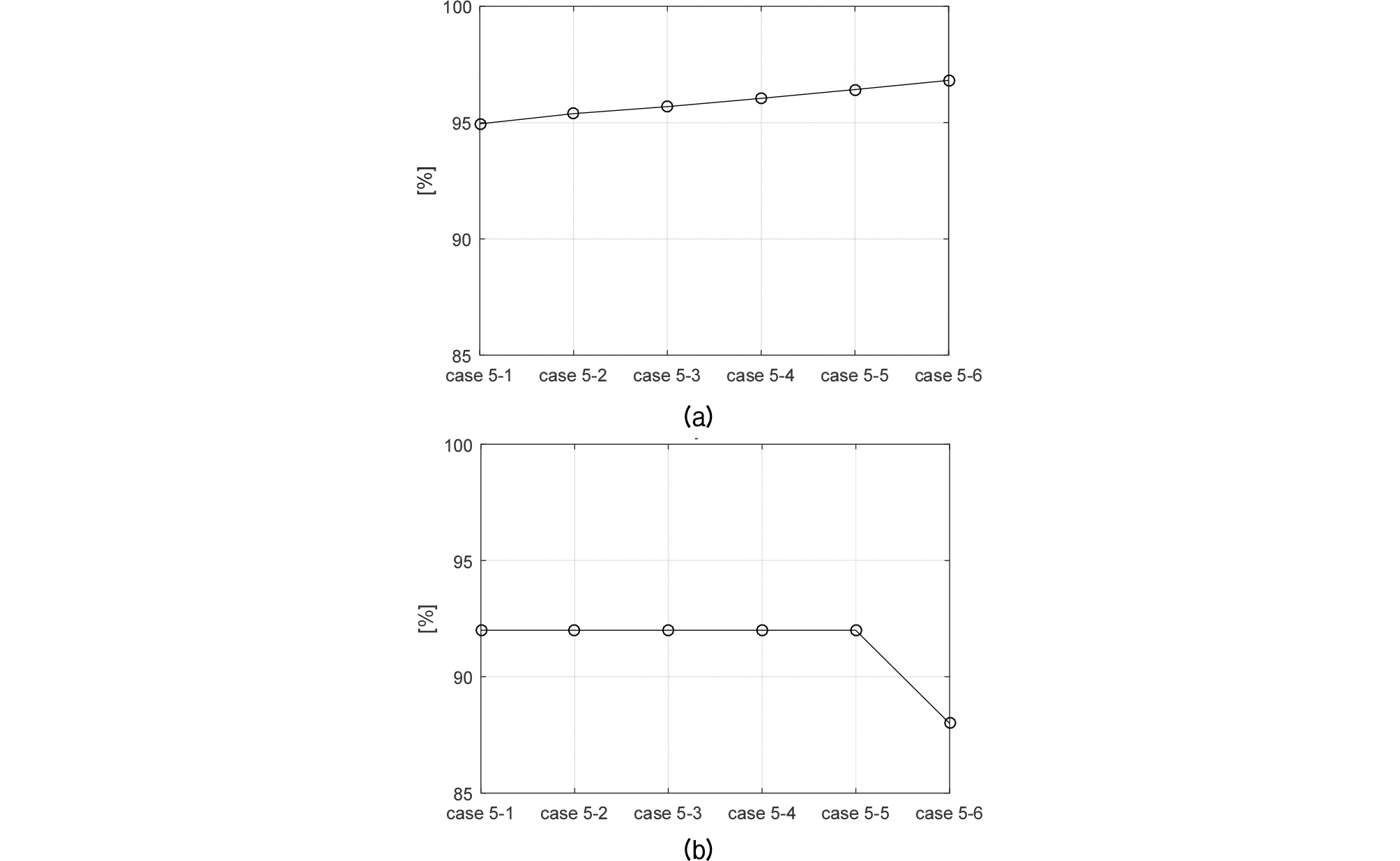
Fig. 8은 Case 4의 실험에서 과도신호에 의한 클러터를 클러스터 길이를 이용하여 제거하고, $K$의 값을 2에서 0.2 간격으로 3까지 바꾸어 실험한 Case 5-1~6의 클러터 제거율과 표적 탐지율이다. Case 4와 과도 신호에 의한 클러스터를 제거한 Case 5-1의 클러터 제거율은 각각 93.74 %와 94.48 %이고, 그 차이는 0.46 %로 크지 않다. 이는 과도신호에 의한 측정치는 국지적으로 나타나 하나의 클러스터로 형성되어 제거되며, 과도 신호가 매 Pulse Repetition Interval (PRI)에서 나타나지 않기 때문이다. Fig. 8(a)과 같이 $K$ 값이 증가할수록 클러터 제거율의 증가폭은 최대 1.81 % 차이로 크지 않지만 증가한다. 그러나 표적 탐지율은 $K$가 3일 때 2.8 이하인 경우보다 4 % 감소하였다. $K$가 증가하면 클러터 제거율은 증가하나, 표적 탐지율은 감소함을 보여준다. 그러나 $K$ 값이 2에서 2.8까지 증가하였을 때 표적 탐지율은 그대로이나 클러터 제거율은 증가하므로, $K$값은 시스템이 목표로 하는 표적 탐지율을 만족하는 최댓값으로 설정하여야 오경보율을 최대한 낮출 수 있다.

Fig. 8.

Clutter reduction rate and target detection rate according to $K$ (a) clutter reduction rate and (b) target detection rate.

V. 결 론

본 논문에서는 연안 환경의 고주파 능동소나에서 클러터에 강인한 소형 표적 탐지 알고리듬을 제안하였다. 소형 표적을 탐지하기 위하여 고주파 능동소나를 사용할 경우 하나의 표적에 대하여 다수의 측정치가 발생한다. 또한 고정된 음원과 수신기를 사용하므로 방파제 등의 연안의 고정된 클러터를 제거하기 위하여 사용된 클러터 맵을 이용한 규준화 기법과 고정된 문턱값의 적용은 해양 생물 및 선박 등의 방사소음에 의한 과도 신호에 취약하다. 본 논문은 이러한 문제점을 해결하기 위하여 측정치 추출 시 문턱값 이상의 첨두치의 통계적 특성을 이용하는 CFAR를 적용하였다. 또한 클러스터링을 적용함으로써 하나의 표적신호에서 생성된 다수의 측정치를 하나로 표현하고, 과도 신호에 의한 측정치를 제거하였다. 제안한 능동소나 탐지 알고리듬은 해상시험 결과를 통하여 클러터 제거율, 표적 탐지 확률로서 검증하였다.