Abnormal sonar signal detection using recurrent neural network and vector quantization

Kibae Lee; Guhn Hyeok Ko; Chong Hyun Lee

doi:10.7776/ASK.2023.42.6.500

Preview

Research Article

The Journal of the Acoustical Society of Korea. 30 November 2023. 500-510
https://doi.org/10.7776/ASK.2023.42.6.500

Abnormal sonar signal detection using recurrent neural network and vector quantization

순환신경망과 벡터 양자화를 이용한 비정상 소나 신호 탐지

Kibae Lee¹

Guhn Hyeok Ko¹

Chong Hyun Lee¹^*

이 기배¹

고 건혁¹

이 종현¹^*

¹제주대학교 해양시스템공학과

^{*Corresponding Author}

ABSTRACT

Passive sonar signals mainly contain both normal and abnormal signals. The abnormal signals mixed with normal signals are primarily detected using an AutoEncoder (AE) that learns only normal signals. However, existing AEs may perform inaccurate detection by reconstructing distorted normal signals from mixed signal. To address these limitations, we propose an abnormal signal detection model based on a Recurrent Neural Network (RNN) and vector quantization. The proposed model generates a codebook representing the learned latent vectors and detects abnormal signals more accurately through the proposed search process of code vectors. In experiments using publicly available underwater acoustic data, the AE and Variational AutoEncoder (VAE) using the proposed method showed at least a 2.4 % improvement in the detection performance and at least a 9.2 % improvement in the extraction performance for abnormal signals than the existing models.

Keywords

Abnormal signal detection

Autoencoder

Vector quantization

Recurrent neural network

수동소나 신호에는 정상신호와 비정상 신호가 같이 존재하는 경우가 대부분이다. 정상신호와 혼재된 비정상 신호는 주로 정상신호만을 학습하는 오토인코더를 이용하여 탐지된다. 하지만 기존의 오토인코더는 혼재된 신호로부터 왜곡된 정상신호를 복원하므로 부정확한 탐지를 수행할 수 있다. 이러한 한계를 개선하고자, 본 논문에서는 순환신경망과 벡터 양자화 기반의 비정상 신호 탐지 모델을 제안한다. 제안된 모델은 학습된 잠재벡터들을 대표하는 코드 북을 생성하고, 제안된 코드벡터의 탐색을 통해 보다 정확하게 비정상 신호를 탐지한다. 공개된 수중 음향 데이터를 이용한 실험에서 제안된 기법이 적용된 오토인코더와 변이형 오토인코더는 기존 모델에 비해 최소 2.4 % 향상된 탐지 성능과 최소 9.2 % 높은 비정상 신호 추출 성능을 보였다.

키워드

비정상 신호 탐지

오토인코더

벡터 양자화

순환신경망

MAIN

I. 서 론
II. 비정상 소나 신호 탐지
2.1 정상 및 비정상 신호
2.2 모델 학습 및 코드 북 생성
2.3 코드벡터 탐색을 통한 비정상 신호 탐지
III. 실험 및 결과
3.1 데이터 구성
3.2 탐지 모델 구현 및 평가
3.3 비정상 신호 탐지 결과
IV. 결 론

I. 서 론

비정상 신호의 탐지는 사전 정의된 정상적 범주를 벗어나는 신호를 검출하는 것으로 의료, 제조업 등 다양한 분야에서 응용되고 있다.^[1,2,3] 비정상 신호 탐지에는 주로 Kernel Density Estimation(KDE), Principle Component Analysis(PCA)와 같은 확률 및 복원 모델이 사용된다.^[4,5] 확률 모델은 학습된 정상신호와 입력된 신호의 확률분포 간 유사도를 계산하고, 복원 모델은 입력 신호에 대한 복원오차를 계산하여 비정상 신호를 탐지한다. 또한 정상신호들이 밀집되는 특징공간을 탐색하는 단일 클래스 분류 모델이 비정상 신호 탐지를 위해 연구되고 있으며, Support Vector Data Description(SVDD)와 One Class Support Vector Machine(OC-SVM)가 포함된다.^[6,7]

최근에는 얕은 학습의 고차원 데이터에 대한 한계를 극복하고자 심층학습 모델의 연구가 수행되고 있다. 비정상 신호 탐지를 위한 대표적인 심층학습 모델에는 Deep SVDD와 오토인코더(AutoEncoder, AE)가 있다. Deep SVDD는 심층학습을 통해 형성된 잠재공간에서 정상신호들을 포함하는 최소 크기의 구 경계를 탐색한다.^[8,9,10] 하지만 Deep SVDD는 탐지 결과에 대한 해석이 용이하지 않아 응용 분야가 제한된다. 반면에, 오토인코더는 입력 신호와 복원된 정상신호 간 차이를 계산하여 해석 가능한 탐지 결과를 제공한다.^[11] 이러한 이유로 오토인코더는 고장 진단, 감시 체계 등 탐지 결과의 해석이 요구되는 분야에서 활발히 응용되고 있다.^[12,13]

비정상 음향 신호 탐지에는 시계열 특징을 학습하는 순환신경망(Recurrent Neural Network, RNN) 기반 오토인코더가 사용된다.^{[14,15,16,17]} 오토인코더는 정상신호의 시계열 특징을 학습하여 복원 오차 기반의 비정상 신호 탐지를 수행한다. 하지만 오토인코더는 입력된 신호가 학습된 매니폴드를 벗어나는 경우에 왜곡된 복원 결과를 출력한다.^[18,19] 따라서 정상과 비정상 신호가 혼재되면 정상신호가 복원되지 못하여 해석 가능한 탐지에 한계를 갖는다. 또한 작은 세기의 비정상 신호가 혼재되면 정상신호의 일부 특징으로 인지되어 탐지성능의 저하를 야기한다.

유사하게, 영상처리 분야에서 오토인코더는 입력 영상과 학습된 영상 간의 미세한 차이로 인해 왜곡된 복원 결과를 출력한다.^[19] 이러한 문제를 해결하고자 입력 영상에 대한 잠재벡터를 학습된 잠재공간으로 이동시키는 벡터 양자화 연구가 수행되고 있으며, 생성 모델에서 우수한 성과를 보이고 있다.^[19,20]

수동소나에서 비정상 신호는 정상신호에 혼재되어 탐지에 어려움을 야기한다. 특히 군사적 위험요소들은 스텔스 기능에 의해 소음을 거의 유발하지 않아 탐지에 한계를 갖는다.^[21] 이러한 이유로 음탐사의 판단을 보조할 수 있는 심층학습 모델의 연구가 활발히 수행되고 있다.^[22,23] 하지만 탐지 결과만을 제공하는 기존 모델들은 오히려 음탐사의 판단에 혼동을 야기할 수 있다. 따라서 본 논문에서는 비정상 신호의 탐지와 추출을 동시에 수행하는 벡터 양자화기반의 오토인코더를 제안한다. 제안하는 모델은 순환신경망을 이용하여 정상신호에 대한 잠재공간을 학습한다. 이후 학습된 잠재벡터들을 이용하여 정상신호의 매니폴드를 대표하는 코드 북을 생성하고, 코드벡터 탐색을 통해 비정상 신호를 탐지한다. 본 논문에서는 공개된 수중 음향 데이터를 이용하여 제안된 알고리즘의 비정상 소나 신호 탐지 성능을 평가한다. 또한 입력 신호와 복원된 정상신호 간 차이로 추출된 비정상 신호를 분석한다.

II. 비정상 소나 신호 탐지

2.1 정상 및 비정상 신호

수동소나에서 비정상 신호는 정상신호에 혼재되어 출현한다. 따라서 시간 $t$ 에 따른 수동소나의 수신신호 $x (t)$ 는 정상과 비정상 상황에 따라 Eq. (1)과 같이 표현된다.

(1)

x (t) = \{\begin{cases} s (t) + u (t), y (t) = 0 \\ s (t) + a (t) + u (t), y (t) = 1 \end{cases},

여기서 $s (t)$ 는 정상신호, $a (t)$ 는 비정상 신호를 의미하며, $u (t)$ 는 정상과 비정상 신호 외의 잡음을 나타낸다. 또한 $y (t)$ 가 0이면 정상 상황, 1이면 비정상 상황을 의미한다.

수중 음향 환경에서 $s (t)$ 는 수동소나의 주 표적신호인 선박신호, $u (t)$ 는 기상 상황에 의해 발생되는 배경소음으로 정의할 수 있다. 또한 $a (t)$ 는 능동 소나, 어뢰 발사음 등 희소 사건에 의해 발생하는 신호로 정의된다. 선박신호는 엔진 및 기타 장비에 의한 기계소음, 프로펠러의 공동현상에 의한 공동소음, 유체와의 마찰에 의한 유체소음으로 구성된다.^[24] 이러한 선박신호는 기계소음에 의한 협대역 고조파 신호 특성과 공동 및 유체소음에 의한 광대역 신호 특성을 동시에 나타낸다. 또한 수중 배경소음은 바람에 의해 해수면에서 발생되는 소음으로 저주파에서 소음준위가 높은 유색잡음 특성을 갖는다.^[25]

2.2 모델 학습 및 코드 북 생성

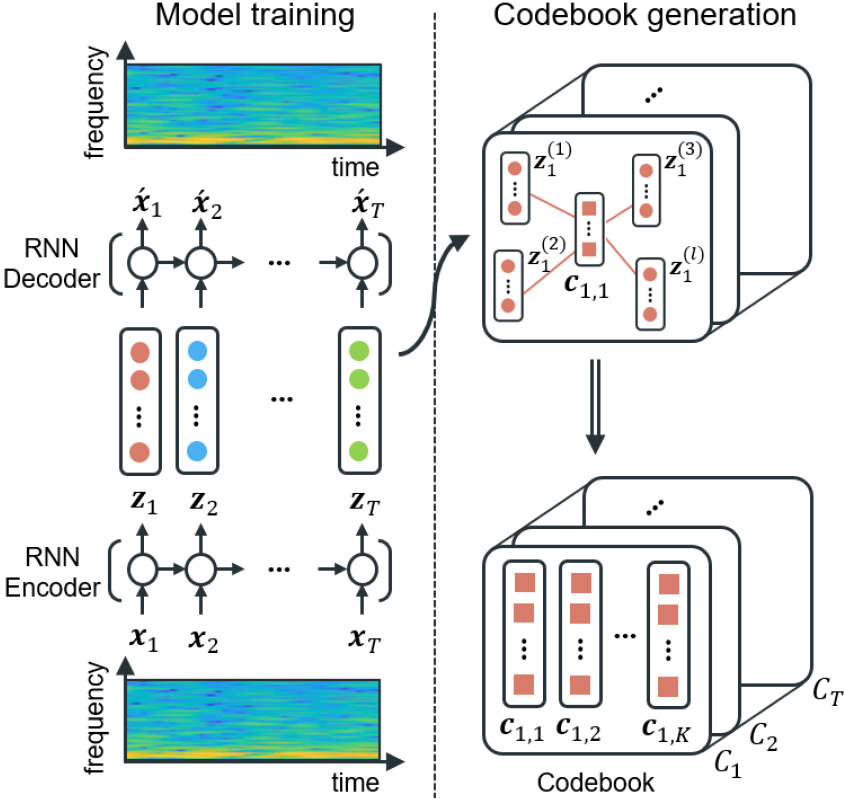
제안하는 비정상 신호 탐지 모델은 Fig. 1과 같이 순환신경망 인코더와 디코더로 구성된다. 인코더는 시간-주파수 특징 $X \in ℝ^{F \times T}$ 를 구성하는 시간에 따른 특징벡터 $x_{t}$ 를 순차적으로 입력받는다. 여기서 $F$ 는 주파수 빈 개수, $T$ 는 시간 샘플 개수를 의미하며, $t = \{1, 2, \dots, T\}$ 이다. 디코더는 시간에 따른 잠재벡터 $z_{t}$ 를 입력받아 복원된 특징벡터 ${\overset{'}{x}}_{t}$ 을 출력한다.

https://cdn.apub.kr/journalsite/sites/ask/2023-042-06/N0660420602/images/ASK_42_06_02_F1.jpg

Fig. 1.

(Color available online) Procedure of model training and codebook generation.

이러한 모델은 학습 방법에 따라 오토인코더와 변이형 오토인코더(Variational AutoEncoder, VAE)로 구분된다. 오토인코더의 학습을 위한 손실함수는 복원 오차를 최소화하는 동시에 $z_{t}$ 가 잠재공간의 중심 $c_{t}$ 에 밀집하도록 Eq. (2)와 같이 정의된다.

(2)

L_{a e} = \frac{1}{T} \sum_{t = 1}^{T} \{{||x_{t} - {\overset{'}{x}}_{t}||}_{2}^{2} + {||z_{t} - c_{t}||}_{2}^{2}\}, c_{t} = \frac{1}{L} \sum_{l = 1}^{L} {z_{t}}^{(l)}, l \in \{1, 2, \dots, L\},

여기서 $c_{t}$ 는 $t$ 시점에서 사전 학습된 잠재공간의 중심으로 계산되며,^[2,9] $z_{t}^{(l)}$ 은 $l$ 번째 학습 데이터에 대한 $t$ 시점의 잠재벡터, $L$ 은 학습되는 데이터 개수를 의미한다.

변이형 오토인코더는 복원 성능의 학습과 동시에 사전 확률 분포 $p (z)$ 를 기준으로 잠재공간을 형성한다.^[26] 변이형 오토인코더의 학습을 위한 손실함수는 Eq. (3)과 같이 시간에 따른 복원 오차, 사후 확률 분포 $q (z_{t} | x_{t})$ 와 $p (z)$ 간 유사도의 합으로 정의된다.

(3)

L_{v a e} = \frac{1}{T} \sum_{t = 1}^{T} \{{||x_{t} - {\overset{'}{x}}_{t}||}_{2}^{2} + D_{K L} (q (z_{t} x_{t}) ∥ p (z))\},

여기서 $D_{K L} (∙)$ 은 Kullback-Leibler(KL) divergence 연산을 의미하며, $p (z)$ 는 평균이 0이고 표준편차가 1인 정규분포로 결정된다.

학습 이후에 학습된 잠재벡터들을 대표하는 벡터 집합인 코드 북 $\{C_{1}, C_{2}, \dots, C_{T}\}$ 을 생성한다. $t$ 시점의 코드 북 $C_{t} = [c_{t, 1}, c_{t, 2}, \dots, c_{t, K}]$ 는 $K$ 개의 코드벡터 , $k \in \{1, 2, \dots, K\}$ 를 열 방향으로 구성한다. 여기서 $K \geq 2$ 이며, $c_{t, k}$ 와 $K$ 는 다음의 절차로 결정된다. 먼저, 잠재공간에서 $c_{t}$ 와 잠재벡터들 간 거리의 합 $d_{t, r e f}$ 를 Eq. (4)와 같이 계산한다.

(4)

d_{t, r e f} = \sum_{l = 1}^{L} ∥ z_{t}^{(l)} - c_{t} ∥_{2}^{2} .

이후 $K$ 를 2부터 점진적으로 증가시키면서 $K$ 평균 군집화를 수행한다. 군집화 과정에서 획득된 $K$ 개의 중심벡터와 클래스 내 잠재벡터들 간의 거리 합 $d_{t} (K)$ 를 Eq. (5)와 같이 계산한다.

(5)

d_{t} (K) = \sum_{k = 1}^{K} \sum_{z_{t}^{(l)} \in w_{t, k}}^{} ∥ z_{t}^{(l)} - c_{t, k} ∥_{2}^{2},

여기서 $c_{t, k}$ 는 $k$ 번째 중심벡터로 갱신되며, $w_{t, k}$ 는 군집화 과정에서 형성된 $k$ 번째 클래스를 의미한다. 끝으로, Eq. (6)과 같이 $d_{t} (K)$ 와 $d_{t, r e f}$ 의 비로 계산되는 $r_{t} (K)$ 가 사전 정의된 임계값 𝜂보다 낮게 수렴하면, $c_{t, k}$ 의 갱신을 중단하고 코드 북을 생성한다.

(6)

r_{t} (K) = d_{t} (K) / d_{t, r e f} .

$η$ 는 0에서 1 사이의 값으로 설정되며, 𝜂가 작을수록 $K$ 는 크게 결정된다.

2.3 코드벡터 탐색을 통한 비정상 신호 탐지

Fig. 2와 같이 잠재벡터를 코드 북 내 탐색된 코드벡터로 대체하여 복원하는 비정상 신호 탐지 기법을 제안한다. 인코더는 특징벡터 $\{{\tilde{x}}_{1}, {\tilde{x}}_{2}, \dots, {\tilde{x}}_{T}\}$ 를 잠재벡터 $\{{\tilde{z}}_{1}, {\tilde{z}}_{2}, \dots, {\tilde{z}}_{T}\}$ 로 변환한다. $\{{\tilde{z}}_{1}, {\tilde{z}}_{2}, \dots, {\tilde{z}}_{T}\}$ 는 제안하는 코드벡터 탐색 절차에 의해 선택된 코드벡터로 대체된다. 먼저, $C_{t}$ 를 구성하는 코드벡터들 간 최대 거리 $ρ_{t}$ 를 Eq. (7)과 같이 계산한다.

(7)

ρ_{t} = \begin{matrix} \max \\ i, j \end{matrix} ∥ c_{t, i} - c_{t, j} ∥_{2}^{2}, i, j \in \{1, 2, \dots, K\},,

여기서 $i$ 와 $j$ 는 $C_{t}$ 를 구성하는 코드벡터들의 인덱스를 의미한다. 이후 Eq. (8)과 같이 ${\tilde{z}}_{t}$ 와 코드벡터들 간의 최소 거리 $δ_{t}$ 를 계산한다.

https://cdn.apub.kr/journalsite/sites/ask/2023-042-06/N0660420602/images/ASK_42_06_02_F2.jpg

Fig. 2.

(Color available online) Procedure of abnormal signal detection and example of code vector search.

(87)

δ_{t} = \begin{matrix} \min \\ k \end{matrix} ∥ {\tilde{z}}_{t} - c_{t, k} ∥_{2}^{2} .

코드벡터 탐색에 의해 사상되는 벡터 ${\hat{z}}_{t}$ 은 $δ_{t} \leq ρ_{t}$ 의 조건이 만족되는 경우에 Eq. (9)와 같이 결정된다.

(9)

{\hat{z}}_{t} = c_{t, n}, n = \begin{matrix} \arg \min \\ k \end{matrix} ∥ {\tilde{z}}_{t} - c_{t, k} ∥_{2}^{2}, δ_{t} \leq ρ_{t} .

반면에 $δ_{t} > ρ_{t}$ 의 조건에서 ${\hat{z}}_{t}$ 은 Eqs. (10)과 (11)과 같이 결정된다.

(10)

{\bar{z}}_{t} = \frac{{\tilde{z}}_{t - 1} + {\tilde{z}}_{t} + τ}{2} .

(11)

{\hat{z}}_{t} = c_{t, n}, n = \begin{matrix} \arg \min \\ k \end{matrix} ∥ {\bar{z}}_{t} - c_{t, k} ∥_{2}^{2}, δ_{t} > ρ_{t},

여기서 ${\bar{z}}_{t}$ 는 과거 및 미래 시점의 잠재벡터 ${\tilde{z}}_{t - 1}$ 와 ${\tilde{z}}_{t + r}$ 에 의해 추정된 벡터이며, $τ$ 는 $δ_{t + τ} \leq ρ_{t + τ}$ 의 조건을 만족하는 가장 작은 양의 정수로 정의된다. Fig. 2에서는 $t$ 가 2인 시점에서 $δ_{t} > ρ_{t}$ 의 조건을 갖는 경우의 코드벡터 탐색 과정을 예시로 보여준다. 끝으로, 제안된 모델의 디코더는 $\{{\hat{z}}_{1}, {\hat{z}}_{2}, \dots, {\hat{z}}_{T}\}$ 을 입력받아 복원된 특징벡터 $\{{\hat{x}}_{1}, {\hat{x}}_{2}, \dots, {\hat{x}}_{T}\}$ 을 출력한다.

오토인코더의 비정상 지수 𝛼는 Eq. (12)와 같이 시간에 따른 복원 오차의 평균으로 계산된다.

(12)

α = \frac{1}{T} \sum_{t = 1}^{T} ∥ {\tilde{x}}_{t} - {\hat{x}}_{t} ∥_{2}^{2} .

변이형 오토인코더의 경우 $\{{\tilde{x}}_{1}, {\tilde{x}}_{2}, \dots, {\tilde{x}}_{T}\}$ 에 대한 사후 확률 분포 $q ({\tilde{z}}_{t} | {\tilde{x}}_{t})$ 와 $p (z)$ 의 KL divergence를 함께 사용하여 Eq. (13)과 같이 𝛼를 계산한다.

(13)

α = \frac{1}{T} \sum_{t = 1}^{T} \{∥ {\tilde{x}}_{t} - {\hat{x}}_{t} ∥_{2}^{2} + D_{K L} (q ({\tilde{z}}_{t} | {\tilde{x}}_{t}) | | p (z))\} .

𝛼는 신호의 비정상적 정도를 나타내며 0에 근접할수록 정상으로 판별된다.

III. 실험 및 결과

3.1 데이터 구성

공개된 수중 음향 데이터를 사용하여 정상과 비정상 상황의 수동소나 신호를 모의하고 제안된 알고리즘을 평가한다. 수동소나 신호는 2.1절에 기술한 정상 및 비정상 상황에 근거하여 ShipEar database^[27]의 선종에 따른 선박신호를 정상신호로 사용하고, DOSITS audio gallery^[28]에 전시된 해저지진, 능동 소나, 어뢰 발사음 신호를 비정상 신호로 사용하여 모의된다. 여기서 정상신호에는 ShipEar database에서 충분한 학습 데이터 확보가 가능한 8종의 선박신호가 사용된다. ShipEar database는 실제 수중 환경에서 측정된 데이터들로 구성되므로 각각의 선박신호에는 수중 배경소음이 포함된다.

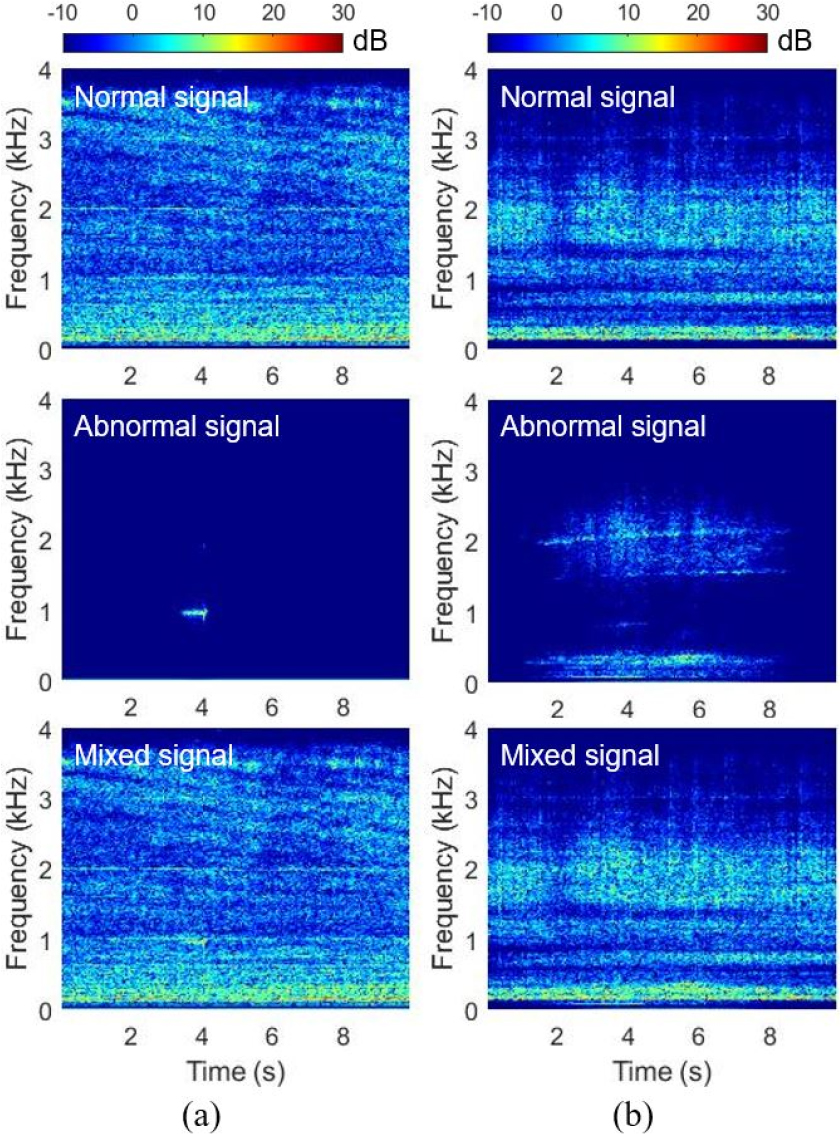
비정상 상황의 수동소나 신호는 10 s 길이의 정상신호에 최소 1 s에서 최대 8 s 동안 지속되는 비정상 신호를 특정 시간 구간에 혼합하여 모의된다. 여기서 비정상 신호는 전압의 실효값을 기준으로 정상신호 대비 0.2에서 1의 비율로 조정되어 서론에 기술한 바와 같이 정상신호와 유사하거나 낮은 세기를 갖는다. Fig. 3은 비정상 신호가 0.6 비율로 혼합된 대표적인 스펙트로그램을 보여준다.

https://cdn.apub.kr/journalsite/sites/ask/2023-042-06/N0660420602/images/ASK_42_06_02_F3.jpg

Fig. 3.

(Color available online) Spectrograms of normal, abnormal and mixed signals. (a) Sail boat and active sonar, (b) passenger and torpedo.

Table 1은 학습 및 평가에 사용되는 모의 신호의 데이터 구성을 보여준다. 수동소나의 정상신호들은 선박신호를 90 % 오버랩하여 10 s 길이로 생성된다. 각 선종 별 학습 데이터는 무작위로 160개가 선택되고, 평가 데이터는 학습 데이터와 신호가 중첩되지 않도록 40개가 선택된다. 비정상 상황의 수동소나 신호는 정상신호를 선종 별로 40개 선택하고 비정상 신호와 혼합하여 생성된다. 따라서 학습 데이터는 총 1,280개의 정상신호로 구성되며, 평가 데이터는 각각 320개의 정상신호와 혼합신호로 구성된다. 여기서 혼합신호는 0.2, 0.4, 0.6, 0.8, 1의 비율로 비정상 신호의 세기를 조정하여 모의되며, 혼합비 별로 각각 320개의 신호가 생성된다.

Table 1.

Underwater acoustic dataset for experiments.

Data type	Train data	Test data
Data type	(Normal)	(Normal)	(Mix)
Dredger	160	40	40
Fishing boat	160	40	40
Motor boat	160	40	40
Mussel boat	160	40	40
Ocean liner	160	40	40
Passanger	160	40	40
RORO ship	160	40	40
Sail boat	160	40	40
Total	1280	320	320

학습 및 평가 데이터는 8,789 Hz 표본화율을 가지며, 단시간 푸리에 변환을 통해 스펙트로그램으로 변환된다. 스펙트로그램은 10 s 길이의 신호에 0.1 s 단위 시간 윈도우와 50 % 오버랩을 적용한 총 198번의 단시간 푸리에 변환으로 생성된다. 변환 과정에서 단시간 푸리에 변환을 통해 표현되는 주파수 간격은 17 Hz로 설정된다. 이와 같이 생성된 256 × 198( $F \times T$ ) 크기의 스펙트로그램은 최소-최대 정규화 과정 거쳐 오토인코더 모델에 입력된다.

3.2 탐지 모델 구현 및 평가

제안하는 알고리즘의 평가를 위해 벡터 양자화 과정을 포함하는 순환신경망 기반 오토인코더 및 변이형 오토인코더를 구현한다. 오토인코더는 병목을 갖는 대칭구조의 인코더와 디코더로 구성되며, 각 층의 순환신경망은 25개의 게이트 순환 유닛(Gate Recurrent Unit, GRU)으로 구성된다. 인코더는 층에 따라 256, 128, 128, 128, 64, 64, 64, 32, 32, 32 길이의 특징벡터를 출력하며, 디코더는 인코더와 대칭되어 특징벡터를 전달한다. 인코더와 디코더 사이의 병목은 인코더에서 출력되는 특징벡터를 입력받아 16길이의 특징벡터를 출력한다. 이후 코드벡터 탐색을 통해 대체된 코드벡터를 디코더에 전달한다. 변이형 오토인코더는 오토인코더와 동일한 구조를 가지며, 병목에서 출력된 32 길이의 특징벡터는 16길이로 샘플링된다. 추가적으로, 코드 북 생성 과정에서 𝜂는 탐지 성능이 수렴하는 0.1로 설정된다.

기존의 비정상 신호 탐지 모델들의 학습 및 평가 방법과 유사하게, 본 논문에서는 10 s 단위로 정상 및 비정상 상황이 표기된 데이터를 이용하여 구현된 모델을 학습 및 평가한다.^[24] 구현된 모델은 약 1.3 s 길이에 해당되는 25개 특징벡터를 순차적으로 처리한다. 따라서 10 s 길이의 데이터를 구성하는 198개의 특징벡터는 구현된 모델에 의해 173번 처리된다. 결과적으로 모델의 학습에는 256 × 25 크기의 스펙트로그램이 총 221,440개 사용된다. 비정상 신호의 탐지 성능은 10 s 데이터에 대한 𝛼 값의 평균으로 계산되는 Area Under the receiver operating characteristic Curve(AUC)로 평가된다.^[29] 또한 실제 비정상 신호와 추출된 비정상 신호의 스펙트로그램 간 mean Intersection over Union(mIoU)를 계산하여 비정상 신호의 추출 성능을 평가한다.^[30] mIoU는 스펙트로그램 상의 실제 신호와 추출된 신호의 합집합 영역과 교집합 영역의 비로 계산된다. 신호의 영역 계산을 위한 임계값은 실제 비정상 신호에 대한 스펙트로그램의 최솟값으로 설정된다.

성능 비교를 위해 기존의 예측, 보간, 복원 모델을 함께 구현한다. 예측 모델은 25개의 특징벡터 중 25번째 특징벡터를 제외한 24개의 특징벡터를 입력받고 25번째 특징벡터에 대한 예측 결과를 출력한다.^[14,15] 예측 모델에서 𝛼는 Eqs. (12)와 (13)의 복원 오차를 25번째 특징벡터에 대한 실제 값과 예측 값의 차이로 대체하여 계산된다.^[14,15] 보간 모델은 25개의 특징벡터 중 13번째 특징벡터를 제외한 24개의 특징벡터를 입력받고 13번째 특징벡터에 대한 보간 결과를 출력한다.^[15] 예측 모델과 유사하게, 보간 모델에서 𝛼는 Eqs. (12)와 (13)의 복원 오차를 13번째 특징벡터에 대한 실제 값과 보간 값의 차이로 대체하여 계산된다.^[15] 예측 및 보간 모델은 입력 시퀀스의 개수가 24개로 변경되고 디코더에서 24번째 셀의 특징벡터만을 출력한다. 복원 모델은 코드벡터 탐색 과정을 제외하여 앞서 구현된 모델과 동일하게 구현되며, 𝛼는 Eqs. (12)와 (13)과 같이 계산된다.

모든 모델들은 32 배치 크기와 1e-4 학습률의 Adam optimizer로 학습되며, 에폭은 5,000으로 설정된다. 학습과 평가에는 ‘NVIDIA GeForce GTX 1070’ Graphical Processing Unit(GPU)이 사용된다. 또한 2.8 GHz 속도의 ‘Intel(R) Core(TM) i5-8400’ 중앙 처리 장치와 16 GB 용량의 Random Access Memory(RAM)이 연산을 위해 사용된다.

3.3 비정상 신호 탐지 결과

모델의 학습 이후 코드 북 생성을 위해 설정되는 𝜂를 0.3부터 0.05까지 감소시키면서 제안하는 모델의 성능을 평가한다. Fig. 4(a)는 오토인코더와 변이형 오토인코더의 모든 혼합비에 대한 평균 AUC를 보여주며, (b)는 학습되는 시간 프레임 개수 대비 $K$ 의 비를 보여준다. (a)에서 오토인코더와 변이형 오토인코더의 평균 AUC는 모두 𝜂가 0.1 이하에서 85.2 %와 87.1 %로 수렴된다. 또한 (b)에서 오토인코더와 변이형 오토인코더의 $K$ 는 2.1 %와 0.8 %로 수렴한다. 여기서 학습되는 시간 프레임 개수는 총 253,440개이며, 오토인코더와 변이형 오토인코더는 𝜂가 0.1인 경우에 각각 5,375개와 2,225개의 코드벡터를 생성한다.

https://cdn.apub.kr/journalsite/sites/ask/2023-042-06/N0660420602/images/ASK_42_06_02_F4.jpg

Fig. 4.

(Color available online) (a) Average AUCs and (b) ratio of $K$ to the number of trained time frames.

Table 2는 모델 별 학습 및 코드 북 생성에 소요되는 평균 시간을 보여준다. 제안하는 모델은 기존 모델들과 달리 코드 북 생성 절차가 요구된다. Table 2에서 제안된 오토인코더와 변이형 오토인코더는 코드 북 생성을 위해 학습 시간 대비 각각 13.5 %와 11.2 %의 시간을 추가적으로 소요한다. 또한 제안된 모델들은 10 s 길이의 데이터 처리에 단지 23.1e-7 s와 19.4e-7 s의 시간을 소요한다.

Table 2.

Average time for model training and codebook generation.

Detection model		Train (s)	Codebook (s)
Prediction models	AE	1,350	-
Prediction models	VAE	1,552	-
Interpolation models	AE	1,348	-
Interpolation models	VAE	1,553	-
Reconstruction models	AE	1,357	-
Reconstruction models	VAE	1,564	-
Proposed models	AE	1,362	184
Proposed models	VAE	1,561	175

Table 3는 비정상 신호의 혼합비에 따른 모델 별 탐지 성능을 10회 평균한 AUC로 보여준다. 혼합비가 0.8 이상인 경우 보간 모델의 오토인코더가 가장 우수한 성능을 보이며, 제안된 변이형 오토인코더와 비교하여 0.4에서 1 % 높은 AUC를 갖는다. 반면에, 혼합비가 0.6 이하인 경우 제안된 변이형 오토인코더는 기존 모델에 비해 최소 3.8 % 높은 성능을 보여준다. 결과적으로, 제안하는 변이형 오토인코더는 모든 혼합비에서 기존 모델 대비 최소 2.4 % 높은 성능을 갖는다.

Table 3.

Average AUCs in % according to mixing ratio of abnormal signals to normal signals.

Mixing ratio	Prediction models		Interpolation models		Reconstruction models		Proposed models
Mixing ratio	AE	VAE	AE	VAE	AE	VAE	AE	VAE
0.2	75.5	75.4	76.6	75.2	74.1	72.2	78.6	81.4
0.4	80.0	79.8	81.6	80.4	78.3	78.0	83.5	86.5
0.6	83.6	83.3	84.8	84.1	84.4	83.2	86.4	88.6
0.8	89.1	88.7	89.4	86.9	87.7	86.5	88.3	89.0
1.0	90.4	89.5	91.2	90.1	90.1	88.7	89.5	90.2
Average	83.7	83.3	84.7	83.3	82.9	81.7	85.2	87.1

기존 모델들이 변이형 오토인코더의 사용으로 저하된 탐지 성능을 보인 것과 다르게, 제안하는 모델은 변이형 오토인코더에서 평균 1.94 % 향상된 성능을 나타낸다. 이는 변이형 오토인코더에서 추정된 확률 분포 간 유사도 지수가 탐지 성능을 향상시키며, 확률적으로 형성된 잠재공간에서의 코드벡터 탐색 과정이 복원 성능을 개선함을 의미한다.

Table 4는 추출된 비정상 신호의 스펙트로그램에 대한 mIoU 평가 결과를 10회 평균하여 보여준다. 제안된 모델들은 모든 혼합비에서 기존 모델들보다 우수한 추출 성능을 나타낸다. 특히 제안된 변이형 오토인코더는 기존 모델들에 비해 최소 9.2 % 높은 mIoU를 가지며, 오토인코더보다 1.2 % 높은 성능을 보인다. Figs. 5와 6은 Fig. 3(a), (b)의 혼합 신호에 대해 기존 오토인코더와 제안된 변이형 오토인코더의 정상신호 복원 및 비정상 신호 추출 결과를 보여준다.

https://cdn.apub.kr/journalsite/sites/ask/2023-042-06/N0660420602/images/ASK_42_06_02_F5.jpg

Fig. 5.

(Color available online) Spectrograms of reconstructed and extracted signals for sail boat and active sonar. (a) Prediction model, (b) interpolation model, (c) reconstruction model, (d) proposed model.

https://cdn.apub.kr/journalsite/sites/ask/2023-042-06/N0660420602/images/ASK_42_06_02_F6.jpg

Fig. 6.

(Color available online) Spectrograms of reconstructed and extracted signals for passenger and torpedo. (a) Prediction model, (b) interpolation model, (c) reconstruction model, (d) proposed model.

Table 4.

Average mIoUs in % according to mixing ratio of abnormal signals to normal signals.

Mixing ratio	Prediction models		Interpolation models		Reconstruction models		Proposed models
Mixing ratio	AE	VAE	AE	VAE	AE	VAE	AE	VAE
0.2	2.8	2.6	3.1	2.7	2.9	1.4	5.1	6.7
0.4	6.0	5.4	7.9	6.9	6.8	6.7	12.8	14.3
0.6	9.1	8.0	10.3	8.2	10.0	8.1	19.0	19.8
0.8	15.8	13.8	16.8	15.0	17.0	14.9	27.4	28.8
1.0	16.5	14.5	17.5	15.7	17.9	16.4	30.6	31.0
Average	10.0	8.8	11.1	9.7	10.9	9.5	18.9	20.1

Fig. 7(a)와 (b)는 3 s에서 5 s 구간과 6 s에서 8 s 구간에 0.4와 0.8 혼합비로 모의된 혼합 신호와 비정상 신호의 스펙트로그램을 보여주며, (c)와 (d)는 최소-최대 스케일링 정규화에 의해 0에서 1의 값으로 표현된 기존 및 제안된 모델의 비정상 지수를 보여준다. (a)와 (b)에서 비정상 신호는 선박신호의 협대역 주파수와 일치되어 어려운 탐지 상황을 모의한다.

https://cdn.apub.kr/journalsite/sites/ask/2023-042-06/N0660420602/images/ASK_42_06_02_F7.jpg

Fig. 7.

(Color available online) Spectrograms of (a) mixed and (b) abnormal signals for input, anomaly scores of (c) the existing models and (d) the proposed models.

Fig. 7(c)에서 예측 모델의 오토인코더는 과거 시점의 특징벡터들을 이용하여 현재 시점의 특징벡터를 예측하므로, 약 5 s에서 6 s 구간의 비정상 지수가 높게 유지됨을 확인할 수 있다. 반면에, 보간 모델의 오토인코더는 과거와 미래 시점의 특징벡터들을 함께 사용하여 약 5 s에서 6 s 구간의 비정상 지수를 예측 모델에 비해 감소시킨다. 하지만 정상신호의 특성 변화에 민감하여 예측 모델에 비해 빈번한 오류를 유발할 수 있다. 또한 복원 모델의 오토인코더는 혼재된 비정상 신호에 의한 왜곡된 복원 결과로 인해, 시간에 따른 비정상 지수의 잦은 변동을 갖는다. 결과적으로, 기존의 모델들은 시간에 따른 신호 탐지 성능에 한계를 나타낸다. 반면에, (d)에서 제안하는 오토인코더는 기존 모델들과 비교하여 시간에 따라 보다 정확한 비정상 지수를 도출하여 오경보를 감소시킬 수 있다. 또한 변이형 오토인코더는 비정상 신호가 없는 구간에서 더욱 낮은 비정상 지수를 나타내어 오토인코더의 정상신호에 대한 탐지 오류를 개선할 수 있다.

IV. 결 론

수중 감시체계에서는 자국 선박 및 항만의 안전을 위해 희소사건에 대한 신속하고 정확한 대응이 요구된다. 이러한 이유로 수동소나 기반의 해석 가능한 비정상 신호 탐지 기술이 요구되고 있다. 수동소나의 비정상 신호는 정상신호로 학습된 오토인코더의 복원 오차를 기반으로 탐지될 수 있다. 하지만 기존의 오토인코더 모델은 정상과 비정상 신호가 혼재된 경우에 왜곡된 정상신호의 복원 결과를 출력하여 탐지 결과의 해석에 한계를 갖는다. 이러한 한계를 개선하고자, 본 논문에서는 순환신경망과 벡터 양자화를 이용한 비정상 신호 탐지 알고리즘을 제안하였다. 제안하는 알고리즘은 잠재공간에서 정상신호의 매니폴드를 대표하는 코드 북을 생성하고, 잠재벡터를 코드 북의 매니폴드로 이동시켜서 복원된 신호의 오차를 계산한다. 공개된 수중음향 데이터를 이용한 실험에서 제안된 모델은 코드 북 생성을 위해 학습 시간 대비 11.2 %의 시간을 추가로 소요하지만, 기존 모델 대비 최소 2.4 % 향상된 탐지 성능과 최소 9.2 % 높은 비정상 신호 추출 성능을 보였다.

제안하는 알고리즘은 수중 감시체계뿐만 아니라 탐지 결과의 해석이 요구되는 의료 진단, 고장 진단 등에도 활용될 수 있을 것이라 기대된다. 또한 향후 수동소나 시스템 적용을 위해 다양한 표적신호와 해상 상황에 따른 실험적 검증과 알고리즘 경량화를 위한 연구가 요구된다.

Acknowledgements

이 논문은 2022학년도 제주대학교 교원성과지원사업에 의하여 연구되었음.

References

L. Ruff, J. R. Kauffmann, R. A. Vandermeulen, G. Monatavon, W. Samek, M. Kloft, T. G. Dietterich, and K. R. Müller, "A unifying review of deep and shallow anomaly detection," Proc. IEEE, 109, 756-795 (2021). 10.1109/JPROC.2021.3052449

K. Lee, C. H. Lee, and J. Lee, "Semi-supervised anomaly detection algorithm using probabilistic labeling (SAD-PL)," IEEE Access, 9, 142972-142981 (2021). 10.1109/ACCESS.2021.3120710

K. Lee, G. H. Ko, and C. H. Lee, "Encoding and decoding-based normalizing flows for image anomaly localization," Electron. Lett. 59, e212829 (2023). 10.1049/ell2.12829

W. Hu, J. Gao, B. Li, O. Wu, J. Du, and S. Maybank, "Anomaly detection using local kernel density estimation and context-based regression," IEEE Trans. Knowl. Data Eng. 32, 218-233 (2020). 10.1109/TKDE.2018.2882404

L. Huang, X. Nguyen, M. Garofalakis, M. I. Jordan, A. Joseph, and N. Taft, "In-network PCA and anomaly detection," Proc. NIPS, 617-624 (2006). 10.7551/mitpress/7503.003.0082

B. Schölkopf, R. Willianson, A. Smola, J. S. Taylor, and J. Platt, "Support vector method for novelty detection," Proc. NIPS. 582-588 (1999).

D. M. Tax and R. P. Duin, "Support vector data description," Machine learning, 59, 45-66 (2004). 10.1023/B:MACH.0000008084.60811.49

C. H. Lee and K. Lee, "Semi-supervised anomaly detection algorithm based on KL divergence (SAD-KL)," Proc. ADIX, 118-123 (2023). 10.1117/12.2661178

L. Ruff, R. A. Vandermeulen, N. Görnits, L. Deecke, S. A. Siddiqui, A. Binder, E. Müller, and M. Kloft, "Deep one-class classification," Proc. ICML, 4393-4402 (2018).

K. Lee, G. H. Ko, and C. H. Lee, "Online anomaly detection algorithm based on deep support vector data description using incremental centroid update," J. Acoust. Soc. Kr. 41, 199-209 (2022).

M. Sakurada and T. Yairi, "Anomaly detection using autoencoders with nonlinear dimensionality reduction," Proc. MLSDA, 4-11 (2014). 10.1145/2689746.2689747

K. Lee and C. H. Lee, "Abnormal signal detection based on parallel autoencoders," J. Acoust. Soc. Kr. 40, 337-346 (2021).

Z. Mnasri, S. Rovetta, and F. Masulli, "Anomalous sound event detection: A survey of machine learning based methods and applications," Multimed. Tools App. 81, 5537-5586 (2022). 10.1007/s11042-021-11817-9

E. Marchi, F. Vesperini, S. Squartini, and B. Schuller, "Deep recurrent neural networks-based autoencoders for acoustic novelty detection," Comput. Intell. Neurosci. 2017, 1-14 (2017). 10.1155/2017/469486028182121PMC5274684

K. Suefusa, T. Nishida, H. Purohit, R. Tanabe, T. Endo, and Y. Kawaguchi, "Anomalous sound detection based on interpolation deep neural network," Proc. ICASSP, 271-275 (2020). 10.1109/ICASSP40776.2020.9054344

Y. Tagawa, R. Maskeliunas, and R. Damasevicius, "Acoustic anomaly detection of mechanical failures in noisy real-life factory environments," Electronics, 10, 2329 (2021). 10.3390/electronics10192329

P. J. Pereira, G. Coelho, A. Ribeiro, L. M. Matos, E. C. Nunes, A. Ferreira, A. Pilastri, and P. Cortes, "Using deep autoencoders for in-vehicle audio anomaly detection," Procedia. Comput. Sci. 192, 298-307 (2021). 10.1016/j.procs.2021.08.031

D. Dehaene, O. Frigo, S. Combrexelle, and P. Eline, "Iterative energy-based projection on a normal data manifold for anomaly localization," Proc. ICLR, 1-17 (2020).

A. Oord, O. Vinyals, and K. Kavukcuoglu, "Neural discrete representation learning," Proc. NIPS, 1-17 (2017).

W. Williams, S. Ringer, T. Ash, J. Hughes, D. MacLeod, and J. Dougherty, "Hierarchical quantized autoencoders," Proc. NIPS, 1-12 (2020).

A New Mindset for the Army: Silent Running, https://www.c4isrnet.com/opinion/2019/12/06/a-new-mindset-for-the-army-silent-running/, (Last viewed September 1, 2023).

S. Kim, S. K. Jung, D. Kang, M. Kim, and S. Cho, "Application of the artificial intelligence for automatic detection of shipping noise in shallow-water" (in Korean), J. Acoust. Soc. Kr. 39, 279-285 (2020).

K. M. Park and D. Kim, "Preprocessing performance of convolutional neural networks according to characteristic of underwater targets" (in Korean), J. Acoust. Soc. Kr. 41, 629-636 (2022).

Y. C. Jung, B. U. Kim, S. K. An, W. J. Seong, K. H. Lee, and J. Y. Hahn, "An algorithm for submarine passive sonar simulator" (in Korean), J. Acoust. Soc. Kr. 32, 472-483 (2013). 10.7776/ASK.2013.32.6.472

L. E. Kinsler, A. R. Frey, A. B. Coppens, and J. V. Sanders, Fundamentals of Acoustics (John Wiley & Sons, New Jersey, 1999), Chap. 15.

D. P. Kingma and M. Welling, "An introduction to variational autoencoders," Found. Trends Mach. Learn. 12, 1-85 (2019). 10.1561/9781680836233

D. S. Dominguez, S. T. Guijarro, A. C. Lopez, and A. P. Gimenez, "ShipEar: An underwater vessel noise database," Appl. Acoust. 113, 64-69 (2016). 10.1016/j.apacoust.2016.06.008

K. J. V. Raposa, G. Scowcroft, J. H. Miller, D. R. Ketten, and A. N. Popper, "Discovery of sound in the sea: Resources for educators, students, the public, and policymakers," in Handbook of The Effects of Noise on Aquatic Life 2, edited by A. N. Popper and A. Hawkins (Springer, New York, 2016).

Y. Koizumi, Y. Kawaguchi, K. Imoto, T. Nakamura, Y. Nikaido, R. Tanabe, H. Purohit, K. Suefusa, T. Endo, M. Yasuda, and N. Harada, "Description and discussion on DCASE2020 challenge task2: unsupervised anomalous sound detection for machine condition monitoring," Proc. DCASE, 81-85 (2020).

H. Rezatofighi, N. Tsoi, J. Y. Gwak, A. Sadeghian, I. Reid, and S. Savarese, "Generalized intersection over union: A metric and a loss for bounding box regression," Proc. CVPR, 658-666 (2019). 10.1109/CVPR.2019.00075

The Journal of the Acoustical Society of Korea 한국음향학회지 ISSN:1225-4428(Print) 2287-3775(Online)

Preview

Abnormal sonar signal detection using recurrent neural network and vector quantization

ABSTRACT

MAIN

(1)

Fig. 1.

(Color available online) Procedure of model training and codebook generation.

(2)

(3)

(4)

(5)

(6)

(7)

Fig. 2.

(Color available online) Procedure of abnormal signal detection and example of code vector search.

(87)

(9)

(10)

(11)

(12)

(13)

Fig. 3.

(Color available online) Spectrograms of normal, abnormal and mixed signals. (a) Sail boat and active sonar, (b) passenger and torpedo.

Table 1.

Underwater acoustic dataset for experiments.

Fig. 4.

(Color available online) (a) Average AUCs and (b) ratio of K to the number of trained time frames.

Table 2.

Average time for model training and codebook generation.

Table 3.

Average AUCs in % according to mixing ratio of abnormal signals to normal signals.

Fig. 5.

(Color available online) Spectrograms of reconstructed and extracted signals for sail boat and active sonar. (a) Prediction model, (b) interpolation model, (c) reconstruction model, (d) proposed model.

Fig. 6.

(Color available online) Spectrograms of reconstructed and extracted signals for passenger and torpedo. (a) Prediction model, (b) interpolation model, (c) reconstruction model, (d) proposed model.

Table 4.

Average mIoUs in % according to mixing ratio of abnormal signals to normal signals.

Fig. 7.

(Color available online) Spectrograms of (a) mixed and (b) abnormal signals for input, anomaly scores of (c) the existing models and (d) the proposed models.

Acknowledgements

References

(Color available online) (a) Average AUCs and (b) ratio of $K$ to the number of trained time frames.