I. 서 론
II. 수신 신호의 모델
III. 송신파형 설계
3.1 상호간섭성의 최소화
3.2 파형의 대역폭 제한조건
3.3 가중치를 이용한 최적화
IV. 송신파형 설계 모의실험
V. 결 론
I. 서 론
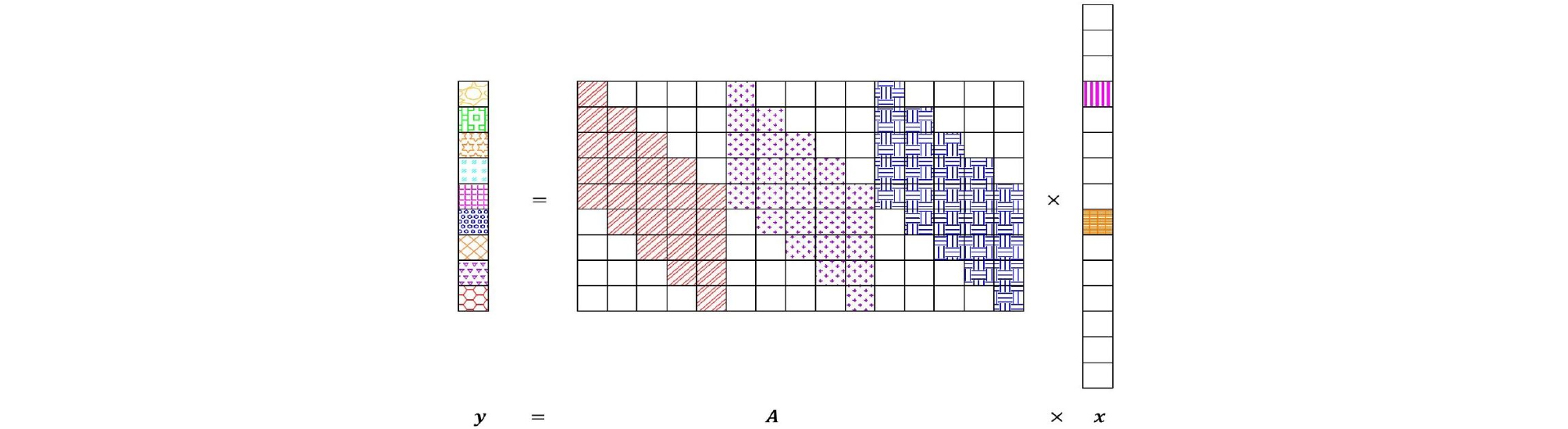
압축센싱의 기본 원리는 희소한 신호를 아주 적은수의 선형측정만으로도 원래의 신호로 복원할 수 있다는 것이다. 즉 과소결정계인 선형시스템에서 희소한 해를 찾는 것으로 다음과 같이 요약할 수 있다.
| $$\mathrm y=\mathbf A\mathrm x,$$ | (1) |
여기서 y를 수신한 측정신호 벡터, A를 표적으로부터 반향된 신호의 시간지연-도플러에 대한 복제벡터들로 구성된 센싱행렬, x를 표적의 반사계수 벡터라고하면, Eq. (1)의 해 x를 구함으로써 표적의 거리와 도플러를 추정할 수 있다. 위 선형시스템에서 압축센싱 기법으로 정확한 해를 찾기 위해서는 두 가지 조건이 필요하다. 첫 번째는 반사계수 x가 충분히 희소한 벡터여야하고 두 번째는 센싱행렬 A가 충분히 비간섭적이어야한다.
본 연구주제인 압축센싱 능동소나를 위한 송신파형 설계와 관련한 연구에 대해 살펴보면 다음과 같다. 레이더와 통신 분야에서 송신파형에 대한 연구가 많이 진행되었다. Stoica을 비롯한 여러 학자들은 송신파형의 ISL(Integrated Sidelobe Level)를 최소화시키는 새로운 알고리즘 CAN(Cyclic Algorithm New) 및 Stopband와 PAR(Peak to Average power Ratio)제약까지 고려한 파형 설계방법을 제안하였다.[1], [2], [3] Zhang을 포함한 여러 학자들은 행렬사영으로 센싱행렬을 최적화하여 송신파형을 설계하는 방법을 제시하였다.[4], [5] 그리고 Zegov는 CAP(Cyclic Algorithm Pruned) 알고리즘을 이용하여 파형 자기상관함수의 간섭성을 최소화함으로써 압축센싱 거리탐지에 대한 송신파형을 도출하였다.[6]그러나 압축센싱 거리-도플러 탐지 관점에서 송신파형을 설계하는 연구는 많지 않다.
본 연구에서는 압축센싱 능동소나 관점에서 센싱행렬이 비간섭적이도록 센싱행렬의 상호간섭성을 낮추는 동시에 시스템이 요구하는 대역폭을 유지하는 송신파형 설계 방법을 제안하였다. 송신파형을 설계하는 주된 원리는 행렬사영법을 이용하여 Gram 행렬 의 비대각 원소들을 최소화하는 파형을 찾는 방법과 소나 송신파형의 대역폭을 제한하는 조건을 결합한 것이다. 모의실험을 통해 본 연구에서 제시한 방법으로 설계된 송신파형의 특성과 성능을 분석하였다.
본 논문의 구성은 다음과 같다. II장에서 수신 신호의 모델을 제시하고 III장에서는 본 논문에서 다룰 송신파형 설계하는 방법을 설명한다. IV장에서는 III장에서 제시한 방법으로 설계된 송신파형의 특성과 성능에 대한 모의실험 결과를 분석하였다. 마지막으로 V장은 결론이다.
II. 수신 신호의 모델
협대역 조건에서 송신한 파형을 라고 할 때, 하나의 표적으로부터 반사된 신호의 모델을 수식으로 나타내면 Eq. (2)와 같다.
| $$a(t)=s(t-\tau)e^{-j2\pi f_dt},$$ | (2) |
여기서 는 시간지연, 는 도플러 주파수이다. 이산화된 송신신호의 길이는 , 시간지연 bin의 개수를 , 도플러 bin의 개수를 , 샘플링 주파수를 , 도플러 해상도를 로 설정하여 Eq. (2)을 이산화하면 이 되고 이 된다(). 그런데 만약 최대 도플러 주파수가 샘플링 주파수를 넘으면 Aliasing이 발생하게 된다. Aliasing이 발생하지 않으려면 조건을 만족해야하고, 최소 조건은 이 된다. 따라서 Eq. (2)은 Aliasing이 발생하지 않은 최소조건을 적용하여 이산화된 식으로 나타내면 다음과 같다.
| $$a _{l,m} =s[ \frac{n}{f _{s}} - \frac{l} {f _{s}} ]e ^{-j2 \pi \frac{m} {M} n}.$$ | (3) |
시간지연과 도플러 편이 행렬을 아래 Eqs. (4)와 (5) 같이 정의하고, 두 행렬의 곱을 Eq. (6)과 같이 정의한다.
| $$\mathbf T_{(L+N-1)\times N}^l=\begin{pmatrix}0_{l\times N}\\{\mathbf I}_{N\times N}\\0_{(L-l-1)\times N}\end{pmatrix},$$ | (4) |
| $$\mathbf F_{N\times N}^m=\begin{pmatrix}w_M^0&0&\dots&0\\0&w_M^1&\ddots&\vdots\\\vdots&\ddots&\ddots&0\\0&\dots&0&w_M^{N-1}\end{pmatrix}^m\left(w_M=e^{-j2\pi/M}\right),$$ | (5) |
| $${\mathbf p}_{l,m}=\mathbf T^l\mathbf F^m.$$ | (6) |
위에서 정의한 시간지연, 도플러 행렬들과 송신신호 벡터 s를 이용하여 Eq. (3) 수신신호의 벡터는 다음과 같이 나타낼 수 있다.
| $${\mathrm a}_{l,m}={\mathbf p}_{l,m}\mathrm s.$$ | (7) |
표적으로부터 반향된 신호 복사본 벡터인 Eq. (7)을 열벡터로 나열하여 다음과 같이 센싱행렬 A를 만들 수 있다.
| $$\mathbf A=({\mathrm a}_{0,0}\vert{\mathrm a}_{1,0}\vert\cdots\vert{\mathrm a}_{\mathrm L-1,\mathrm M-1})=\mathbf P\odot\mathrm s,$$ | (8) |
여기서 ( )안의 기호는 나열하는 열벡터의 구분선이다. 이며, 연산은 Hadamard product와 유사하게 아래와 같이 정의한다.
| $$\begin{array}{l}(\mathbf H\vert\mathbf I)\odot z=(\mathbf Hz\vert\mathbf Iz),\\\lbrack(\mathbf H\vert\mathbf I)\odot z\rbrack^H=z^H\odot(\mathbf H\vert\mathbf I)^H.\end{array}$$ | (9) |
위의 H, I는 임의의 행렬, z는 임의의 벡터, 는 켤레 전치 연산자이다.
x를 시간지연-도플러 에 해당하는 표적에 대한 반사계수 벡터라 할 때, 다음과 같이 정의한다.
| $$x=\lbrack x_{0,0},x_{1,0},...,x_{L-1,M-1}\rbrack^T.$$ | (10) |
위의 센싱행렬 A와 표적의 반사계수 벡터 x와 잡음 성분 을 이용하여 수신 신호 모델을 구성하면 Eq. (11)와 Fig. 1과 같이 표현할 수 있다.
| $$\mathrm y=\sum_{l=0}^{L-1}\sum_{m=0}^{M-1}{\mathrm x}_{l,m}{\mathrm a}_{l,m}+\epsilon=\mathbf A\mathrm x+\epsilon,$$ | (11) |
여기서 센싱행렬 A의 크기는 이다. y는 능동 소나의 관측된 수신 신호 벡터이며, x는 표적의 반사계수를 의미하는 (LM) × 1 벡터, 는 (L+N-1) × 1 잡음 벡터이다.
잡음이 추가된 최종 수신신호 벡터 y에 내포되어 있는 표적의 정보인 희소한 벡터 x는 OMP(Orthogonal Matching Pursuit)와 같은 Greedy 알고리즘[7]과 BPDN(Basis Pursuit Denoising)[8]과같은 복구 알고리즘을 이용해서 구할 수 있다. Greedy 알고리즘은 greedy한 특성 기반의 l0-norm 최소화 방식으로 해를 구하며 수식으로 표현하면 다음과 같다.
| $$\min\parallel x\parallel_0s.t.\parallel y-\mathrm Ax\parallel_2^2\leq\epsilon,$$ | (12) |
여기서은 -norm을 나타내며 행렬이나 벡터의 0이 아닌 원소의 개수이다. 그리고 은 측정값의 잡음을 고려해주는 오차의 크기이다. 반면에 BPDN은 최적화 이론 기반의 l1-norm 최소화 방식으로 해를 구하며 수식으로 표현하면 다음과 같다.
| $$\min\parallel x\parallel_1s.t.\parallel y-\mathrm Ax\parallel_2^2\leq\epsilon,$$ | (13) |
여기서 은 행렬이나 벡터의 -norm을 나타내며 모든 원소의 절대값의 합이고, 은 -norm을 나타내며 모든 원소의 제곱의 합이다. 본 논문에서는 Eq. (11)을 BPDN을 이용하여 공식화하였으며, CVX(Convex programming)를 이용하여 계산할 것이다.[8]
III. 송신파형 설계
본 논문에서 다룰 송신파형 설계는 센싱행렬이 비간섭적이도록 센싱행렬의 상호간섭성을 낮추면서, 압축센싱 능동소나 시스템이 요구하는 대역폭을 유지하는 두 과정을 결합한 방법이다. 3.1절에서 Gram 행렬을 이용하여 센싱행렬의 상호간섭성을 낮추는 송신파형을 설계하는 과정을 다루고, 3.2절에서는 DFT 매트릭스를 이용하여 원하는 대역폭을 유지하는 송신파형을 설계하는 과정을 다룬다. 마지막으로 3.3절에서는 3.1절과 3.2절에서 다룬 두 과정을 가중치를 이용하여 통합한다.
3.1 상호간섭성의 최소화
RIP(Restricted isometry property) 조건은 잡음이 추가된 압축센싱 문제에서 해를 안정적으로 찾는 것을 보장한다.[10] RIP 조건은 아래의 부등식으로 표현된다.
| $$(1-\delta_k)\parallel\mathrm x\parallel_2^2\leq\parallel\mathbf A\mathrm x\parallel_2^2\leq(1+\delta_k)\parallel\mathrm x\parallel_2^2.$$ | (14) |
원소의 개수가 개인 희소한 모든 x에 대해서 위 부등식을 만족하는 가 0과 1사이에 존재하면 RIP 조건이 성립되는 것이다. 그러나 RIP 조건이 만족하는지 확인하는 것은 모든 x에 대해 조사해야하는 비결정 난해문제가 되므로 확인하기 어렵다. 따라서 센싱행렬의 비간섭성을 평가하기 위해 RIP 조건을 확인하는 방법의 대안으로 상호간섭성을 사용한다.[11]상호간섭성의 정의는 센싱행렬 에서 서로 다른 열벡터 사이의 내적값 중 최댓값이며 아래의 식으로 표현된다.
| $$\mu(\mathbf A)=\begin{array}{c}\max\\i\neq j\end{array}\frac{\vert\mathbf A_i^H{\mathbf A}_j\vert}{\parallel{\mathbf A}_i\parallel_2\parallel{\mathbf A}_j\parallel_2},$$ | (15) |
여기서 와 는 각각 행렬 의 번째 열벡터이다. 이론적으로 는 범위안에 있고 값이 작을수록 행렬 A의 열벡터들 사이의 직교성이 높다는 의미가 된다.[11]그리고 상호간섭성과 RIP 조건은 매우 밀접한 연관성을 갖는다. x의 0이 아닌 원소의 개수()와 가 아래의 Eq. (16)과 같은 부등식을 만족하면 를 만족하는 유일해를 보장하고 RIP 조건도 성립된다.[11]
| $$\parallel\mathrm x\parallel_0<\frac12\lbrack1+\frac1{\mu(\mathbf A)}\rbrack.$$ | (16) |
상호간섭성의 특성을 살펴보았을 때 상호간섭성은 압축센싱 문제의 해를 찾는 과정에서 복구 정확성에 매우 큰 영향을 주는 것을 알 수 있다. 결국 센싱행렬 A의 상호간섭성을 작게 만들수록 RIP 조건이 만족하게 되고, 압축센싱 문제의 해가 높은 확률로 복구가 성공된다고 할 수 있다. 그러나 압축센싱 능동소나의 송신파형을 설계할 때 직접적으로 상호간섭성을 조절하기는 어렵다.
Gram 행렬 을 계산해보면 행렬 A의 열벡터들 사이의 모든 내적값들이 Gram 행렬의 원소들로 구성된다. 따라서 본 논문에서는 Gram 행렬 를 이용하여 상호간섭성을 낮추고자 한다. 여기서 송신파형의 크기가 동일( )하다면 Gram 행렬의 모든 대각원소는 신호의 길이인 이 된다. 그러므로 대각 원소는 모두 이고 비대각 원소는 모두 0인 NI 행렬이 이상적으로 최소의 상호간섭성을 갖는 Gram 행렬이 된다. 이때, 송신파형 s를 조절하여 Gram 행렬 를 이상적인 NI 행렬에 근사시키는 과정은 다음과 같은 식으로 나타낼 수 있다.
| $$\begin{array}{c}\arg min\\\mathrm s\end{array}\left\|G-N\mathrm I\right\|_F^2,$$ | (17) |
여기서 는 Frobenius norm을 의미하고 이 된다.
Eq. (17)은 벡터 에 관한 4차항의 식이 되어 최적 해를 구하기 매우 어렵다. 따라서 벡터 에 관한 2차항의 식으로 간소화하는 방법을 도입하여 최적 해에 접근한다.[1]
| $$\begin{array}{c}\arg min\\\mathrm s,\;\mathrm U\end{array}\left\|\mathrm P\odot\mathrm s-\mathrm U\sqrt N\right\|_F^2,$$ | (18) |
여기서 U는 semi-unitary 행렬이다. 송신파형 s의 크기가 단일하다는 제약을 포함하여 Eq. (18)은 다음과 같이 정리된다.
Eq. (19) 최소화 문제를 풀기위해 한가지 변수를 고정하고, 다른 변수를 계산하는 과정을 번갈아가면서 수렴할 때까지 반복하는 행렬사영법을 도입했다.[5]먼저 송신파형 s가 주어져 있을 경우 을 최소화 시키는 U는 다음과 같다.
| $$\mathbf U={\mathbf U}_1\mathbf U_2^H,$$ | (20) |
여기서 U1과 U2는 의 특이값 분해를 통해서 얻을 수 있다.[1], [5]
| $$\mathbf P\odot\mathrm s\sqrt N={\mathbf U}_1\boldsymbol\Sigma\mathbf U_2^H,$$ | (21) |
여기서 U1은 unitary 행렬, U2는 semi-unitary 행렬, 그리고 는 특이값 대각행렬이다. 변수 U가 고정되어 있을 때 Eq. (19)의 값이 0으로 최솟값을 갖는 경우는 아래와 같다.
| $$\mathbf P\odot\mathrm s=\mathbf U\sqrt N.$$ | (22) |
Eqs. (20)과 (21)를 통해 구한 변수 U를 고정하고, Eq. (19)를 최소화시키는 변수 s는 아래와 같은 과정으로 구한다. Eq. (22)은 행렬을 벡터화시키는 과정을 통해서 아래 Eq. (23)과 같이 재구성할 수 있다.
| $$\mathbf P'\mathrm s=\mathrm q,$$ | (23) |
| $$\mathbf P'=(\mathbf p_{0,0}^T\vert\mathbf p_{0,0}^T\vert\cdots\vert\mathbf p_{L-1,M-1}^T)^T,$$ | (24) |
| $$\mathrm q=\mathrm{vec}\sqrt N\mathbf U\rbrack,$$ | (25) |
여기서 vec은 행렬을 세로 벡터로 바꾸는 벡터화 연산이다.
이때, 위 식으로부터 송신파형 s는 최소자승법을 통하여 다음과 같이 구할 수 있다.
| $$\mathrm s=(\mathbf P'^H\mathbf P')^{-1}\mathbf P'^H\mathrm q.$$ | (26) |
마지막으로 크기제약()이 있으므로 최종 파형 s는 다음과 같이 표현된다.
| $$\mathrm s=\exp(j\bullet\arg(\mathrm{s})).$$ | (27) |
3.2 파형의 대역폭 제한조건
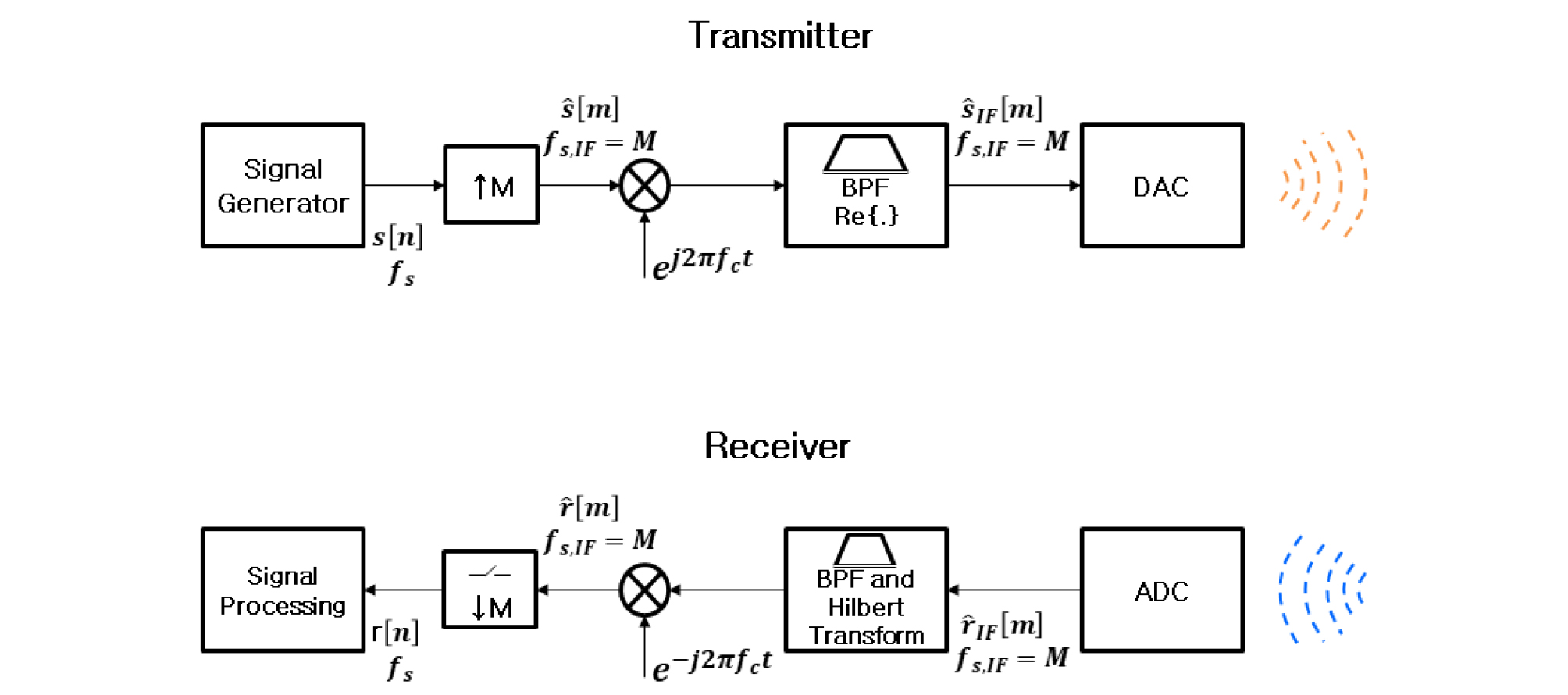
소나 시스템에서 간소화된 디지털 신호의 송수신 과정은 Fig. 2와 같다.[6]샘플링 주파수 만큼 생성된 최초 신호 은 배 만큼 업샘플링한 후 반송 주파수 와 혼합한다. 혼합된 신호 은 대역통과필터를 통과시키고 디지털-아날로그 변환기를 통해 아날로그로 변환되어 송신된다. 수신과정은 수신한 아날로그 신호를 아날로그-디지털 변환기를 통해 디지털로 변환 후에 대역통과 필터를 통과시킨다. 통과된 신호를 기저대역으로 옮겨주고 다운 샘플링한 후 신호처리하여 표적의 정보를 추정한다. 따라서 송신파형은 실제 소나시스템에서 대역통과 필터를 통과하기 때문에 시스템이 요구하는 대역폭을 유지해야한다.
본 논문에서는 DFT(Discrete Fourier Transform) 행렬을 이용하여 원하는 주파수 밴드를 유지하고, 원하지 않는 주파수 밴드는 억압함으로써 시스템이 요구하는 대역폭을 갖는 송신파형을 설계하고자 한다. 설계하는 과정은 다음과 같다.[3]
송신파형의 전체 주파수 밴드에서 억압해야하는 주파수 밴드를 다음과 같이 표현할 수 있다.
| $$Ω=(f_{11},f_{12}),$$ | (28) |
여기서 와 는 각각 하한과 상한 주파수를 나타낸다. DFT 주파수 그리드의 포인트가 촘촘하게 커버할 수 있도록 충분하게 큰 를 정해준다. 을 DFT 행렬이라고 정하면 (k,l)번째 원소는 아래와 같이 기술할 수 있다.
| $$\lbrack F_\widetilde N\rbrack_{kl}=\frac1{\sqrt{\widetilde N}}\exp(j2\pi\frac{kl}{\widetilde N}),k,l=0,...,\widetilde N-1,$$ | (29) |
여기서 계수 은 을 유니터리 행렬로 만들어 준다. 범위에 있는 주파수에 해당하는 의 열들로 이루어진 행렬을 로 설정하면, 에서 Q를 제외한 열들로 이루어진 행렬을 R로 설정할 수 있다. 범위에 있는 의 스펙트럼 전력을 설정한 Q를 이용하여 억제하는 것을 Eq. (30)을 최소화 시키는 것으로 표현할 수 있다.
| $$\parallel\mathbf Q^H\widetilde s\parallel^2,$$ | (30) |
| $$\widetilde{\mathrm s}=\left[\mathrm s(1)\cdots\mathrm s(N)\underbrace{0\cdots0}_{\widetilde N-N}\right]{}^T.$$ | (31) |
만약 가 QH의 0공간 안에 놓여있으면 Eq. (30)은 0이 된다. DFT 행렬의 성질에 따라 QH의 0 공간은 R의 열들로 확장할 수 있기 때문에 Eq. (30)의 최소화는 다음 Eq. (32)식으로 재구성할 수 있다.
여기서 는 임의의 변수 벡터이다.
Eq. (32) 최소화 문제를 풀기위해 Eq. (19)과 마찬가지로 행렬사영법을 도입했다.[5]먼저 송신파형 s가 주어져 있을 경우 를 만족하므로 을 최소화시키는 는 다음과 같다.
| $$\alpha=\mathbf R^H\widetilde{\mathrm s}.$$ | (33) |
변수 가 고정되어 있을 때 Eq. (32)의 값이 0으로 최솟값을 갖는 경우는 아래와 같다.
| $$\widetilde{\mathrm s}=\mathbf R\mathrm\alpha,$$ | (34) |
여기서 는 s를 영 삽입한 것이므로 Eq. (32)을 최소화하는 송신파형 s는 의 첫 번째부터 번째 원소가 된다.
| $$\mathrm s=\widetilde{\mathrm s}(1)\cdots\widetilde{\mathrm s}(N)\rbrack^T.$$ | (35) |
마지막으로 파형의 크기제약() 이 있으므로 최종 파형 는 다음과 같다.
| $$\mathrm s=\exp(j\bullet\arg(\mathrm s)).$$ | (36) |
3.3 가중치를 이용한 최적화
앞서 3.1절과 3.2절에서 다룬 Eq. (19)와 Eq. (32)를 결합함으로써, 상호간섭성과 대역폭을 통합하여 다루는 최소화 문제를 다음과 같이 수식적으로 나타낼 수 있다.
여기서 는 과 에 상대적인 가중치를 주는 변수이다. 세가지 변수로 이루어진 는 식을 최소화시키는 한가지 변수를 차례로 적용하고 갱신하는 과정을 반복함으로써 해결할 수 있다.
위의 설명과 행렬사영법을 기본으로 송신파형 최적화 과정은 아래와 같이 요약할 수 있다.[2]
⦁ 0 단계 : 을 ()을 만족하는 랜덤 시퀀스 또는 기존 시퀀스1)로 초기화한다.
1) LFM 시퀀스, Golomb 시퀀스 등
⦁ 1 단계 : 고정된 s와 U에서, 은 의 2차 볼록함수이다. 따라서 , 를 적용하여 를 최소화하는 를 얻는다.
| $$\alpha=\mathbf R^H\widetilde{\mathrm s}.$$ | (38) |
⦁ 2 단계 : 고정된 s와 에서, 를 최소화하는 U는 의 특이값 분해를 이용해서 구한다.
| $$\mathbf U={\mathbf U}_1\mathbf U_2^H.,\;\mathbf A\sqrt N={\mathbf U}_1\boldsymbol\Sigma\mathbf U_2^H.$$ | (39) |
⦁ 3 단계 : 고정된 와 U에서, 는 다음과 같이 쓸 수 있다.
| $$J=const-2Re[{s} ^{H} [ \lambda c _{1} +(1- \lambda )c _{2} ]],$$ | (40) |
여기서 은 의 첫 번째부터 번째까지 원소이고 는 이다. 그렇다면 를 최소화하는 는 다음과 같다.
| $$\mathrm s=\exp\{{j\bullet\arg\lbrack\mathrm\lambda c_1+(1-\mathrm\lambda)c_2\rbrack}\}.$$ | (41) |
⦁ 반복단계 : 1, 2, 3단계를 수렴조건이 만족할 때까지 반복한다. (예 : 여기서 는 번째 반복에서 얻은 파형이고, 는 미리 정한 오차 한계이다.)
IV. 송신파형 설계 모의실험
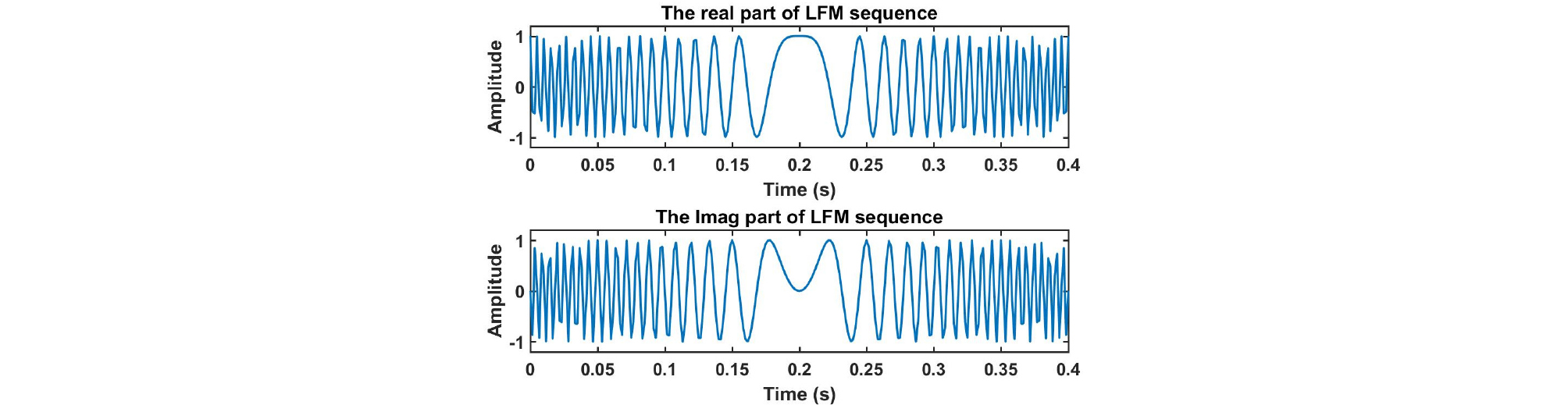
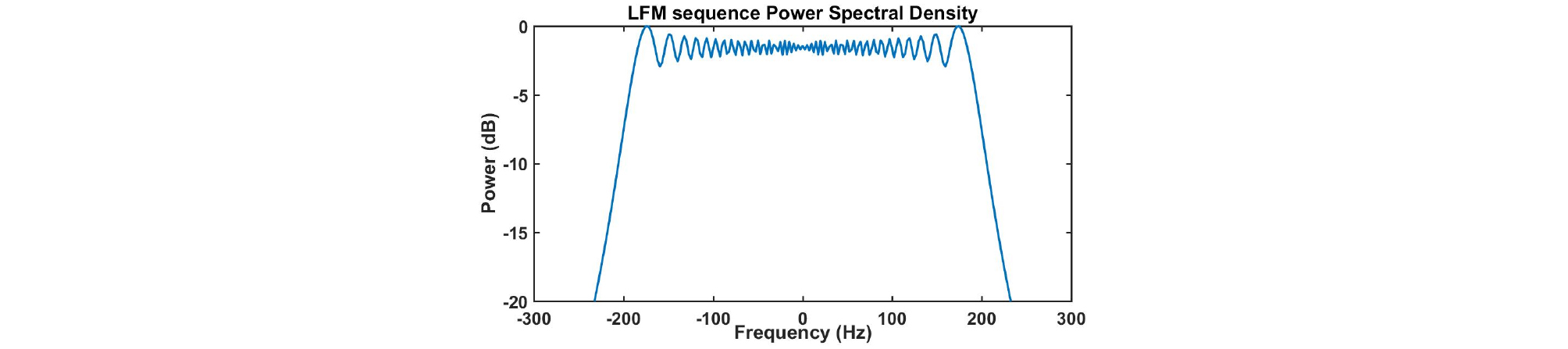
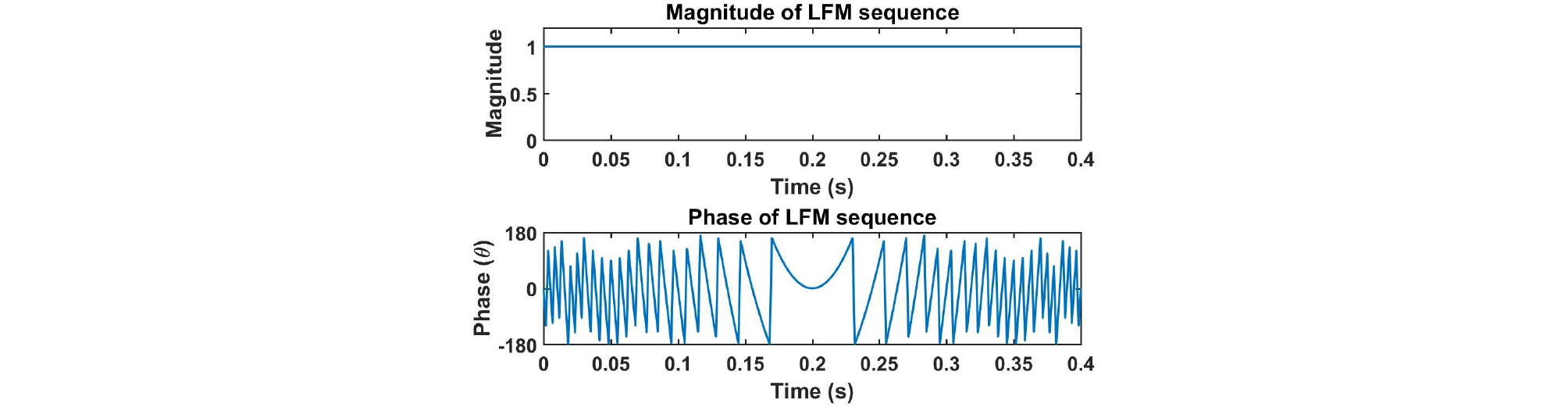
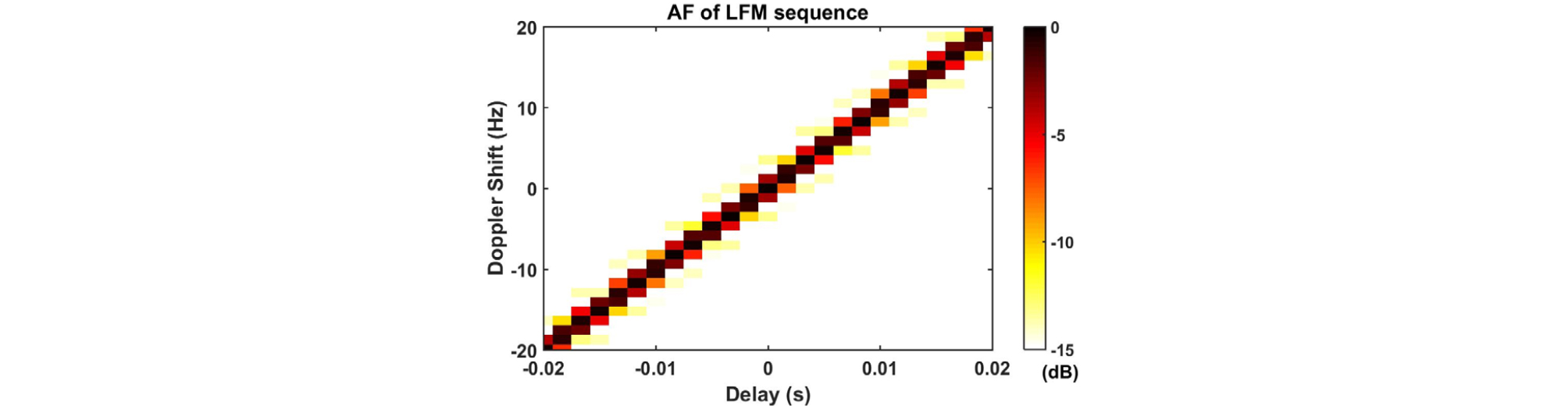
III장에서 제시한 송신파형을 설계하는 방법을 검증하기 위해 모의실험을 진행하였다. 초기 신호는 LFM, 펄스시간 0.4 s, 대역폭 400 Hz, 샘플링 주파수() 600 Hz, 신호의 길이 으로 설정하였다. 파형 설계를 진행하기 위한 조건들은 시간지연 bin의 개수 , 도플러 bin의 개수 , , , 오차한계 로 설정하였다. 초기신호의 시간과 주파수 영역 그림은 Figs. 3과 4와 같고, 신호의 절대값 크기와 위상을 나타낸 그림은 Fig. 5, 모호함수를 확대한 그림은 Fig. 6과 같다. 모호함수를 통해서 LFM신호는 시간지연-도플러의 간섭성이 높은 것을 알 수 있다. 그리고 LFM 신호를 이용하여 생성한 센싱행렬 A의 상호간섭성 값은 0.85이다.
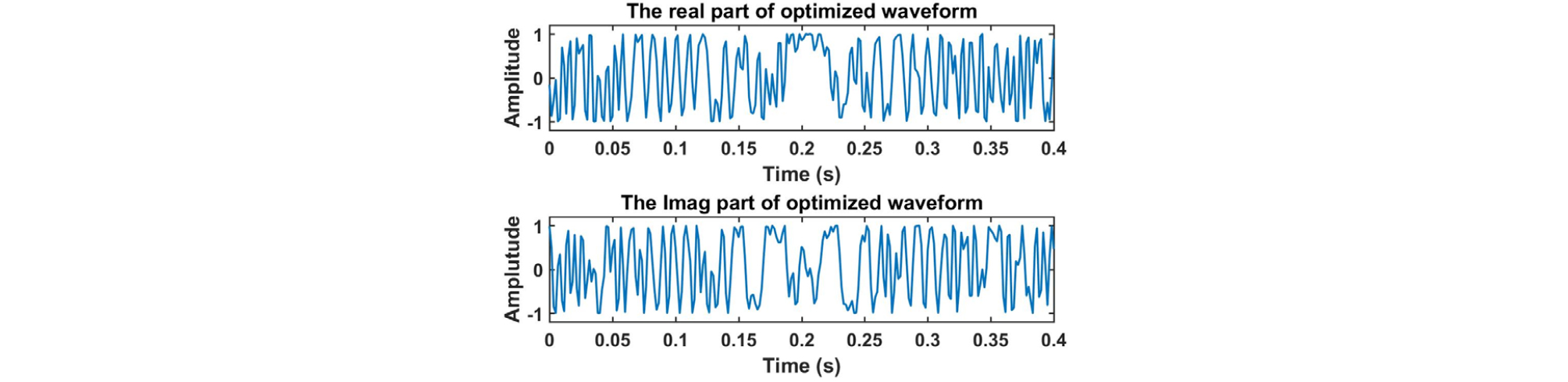
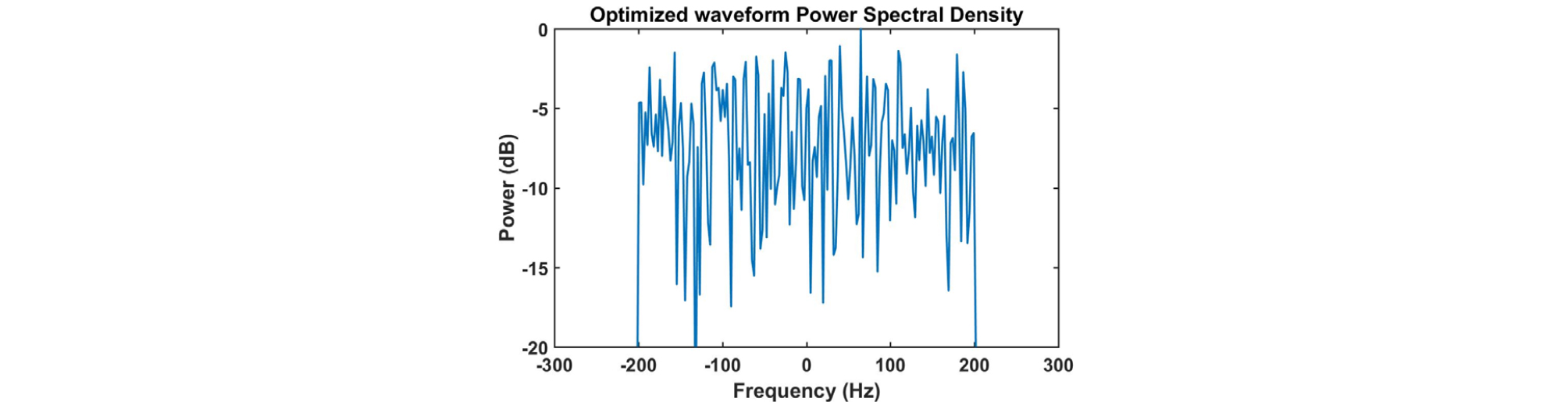
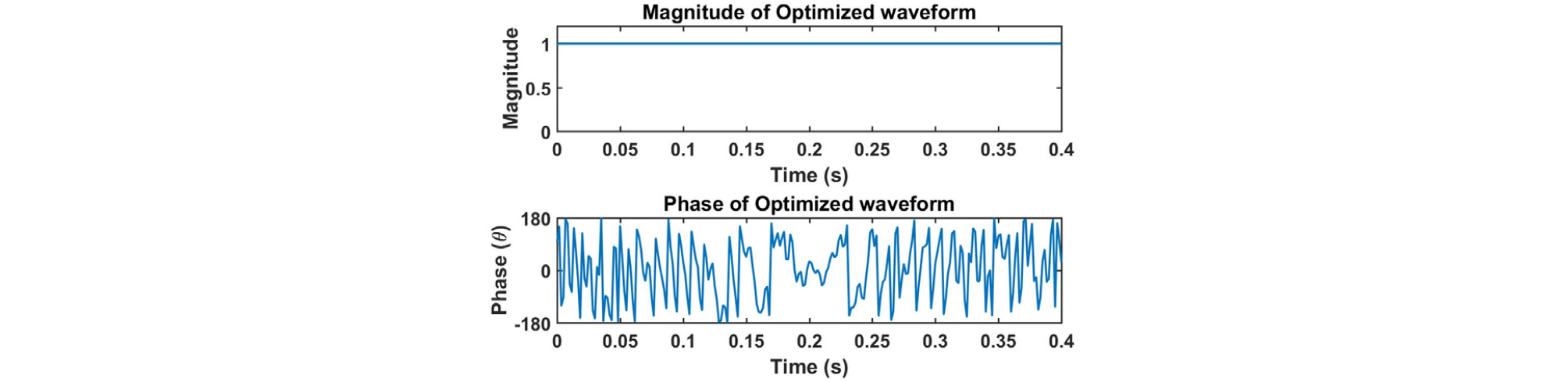
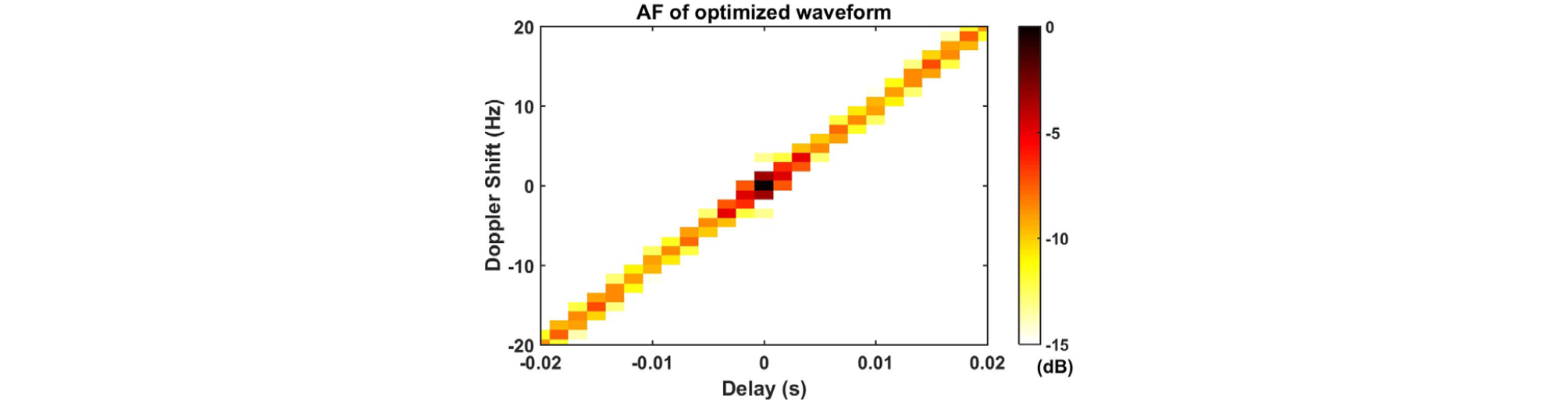
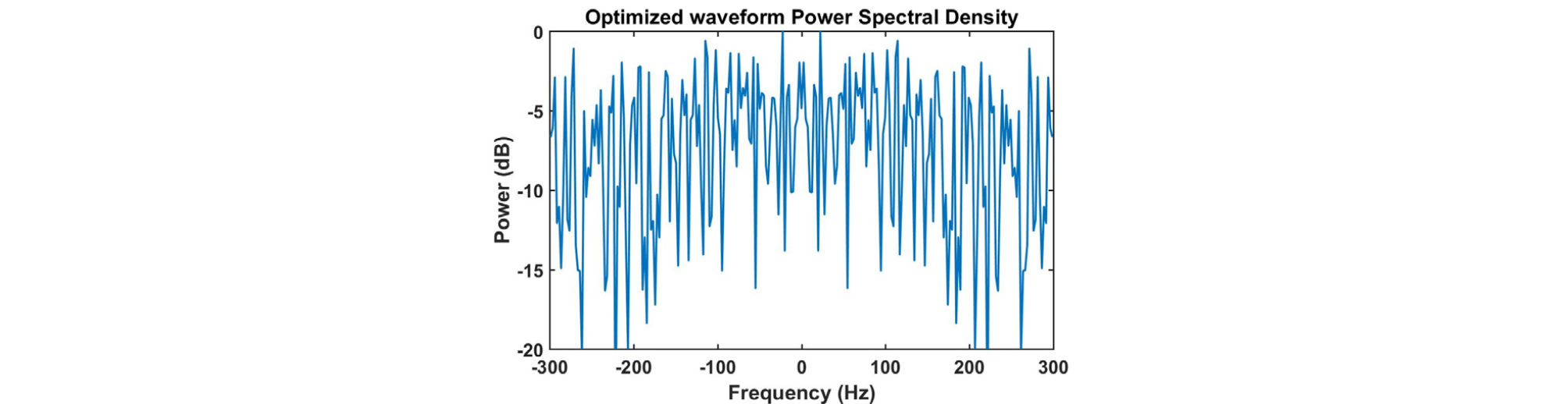
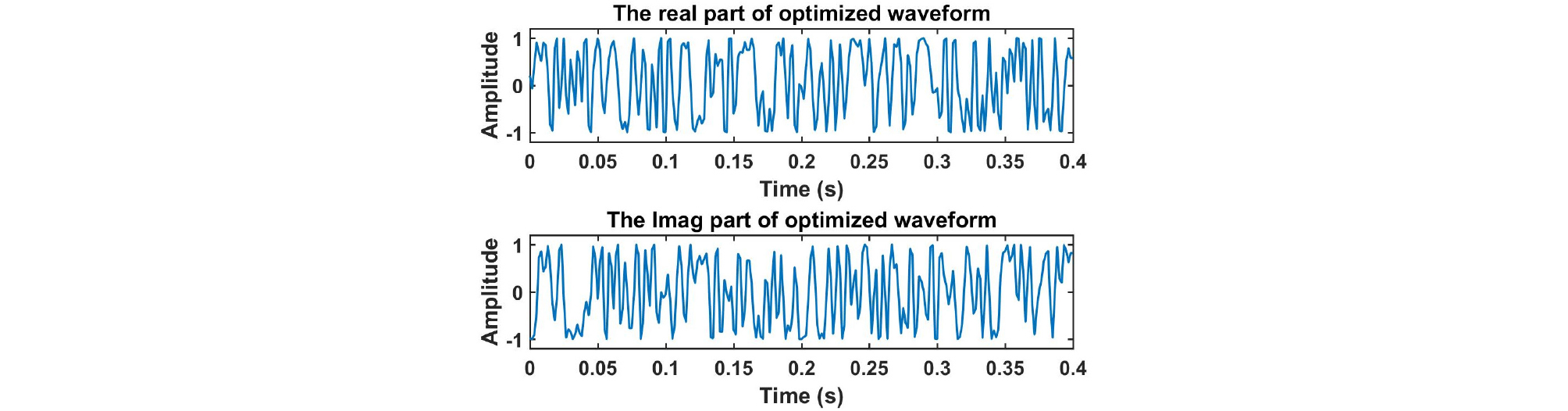
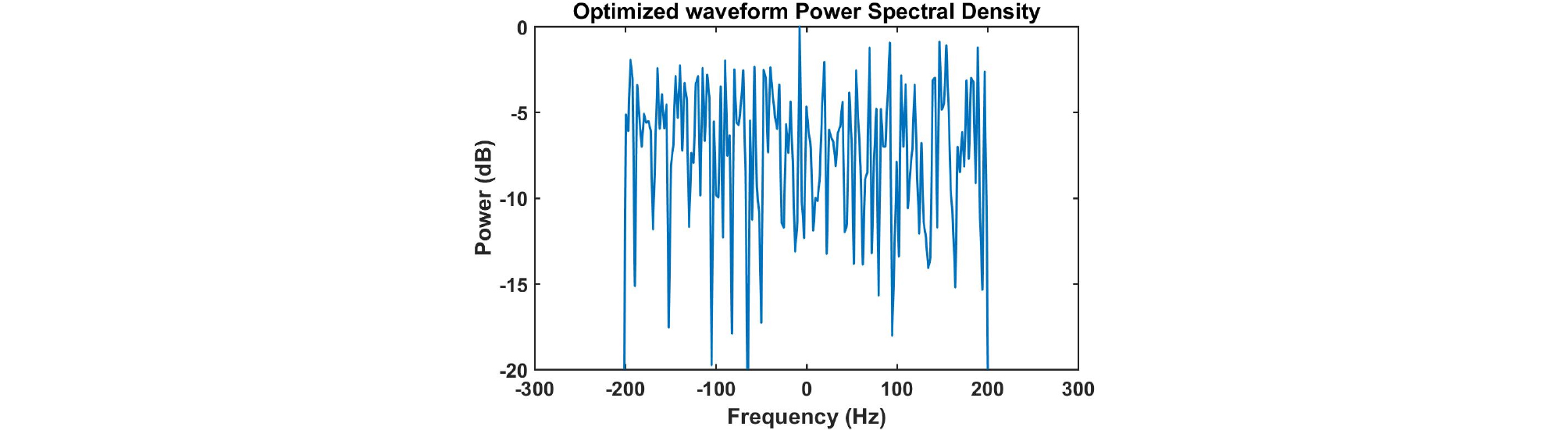
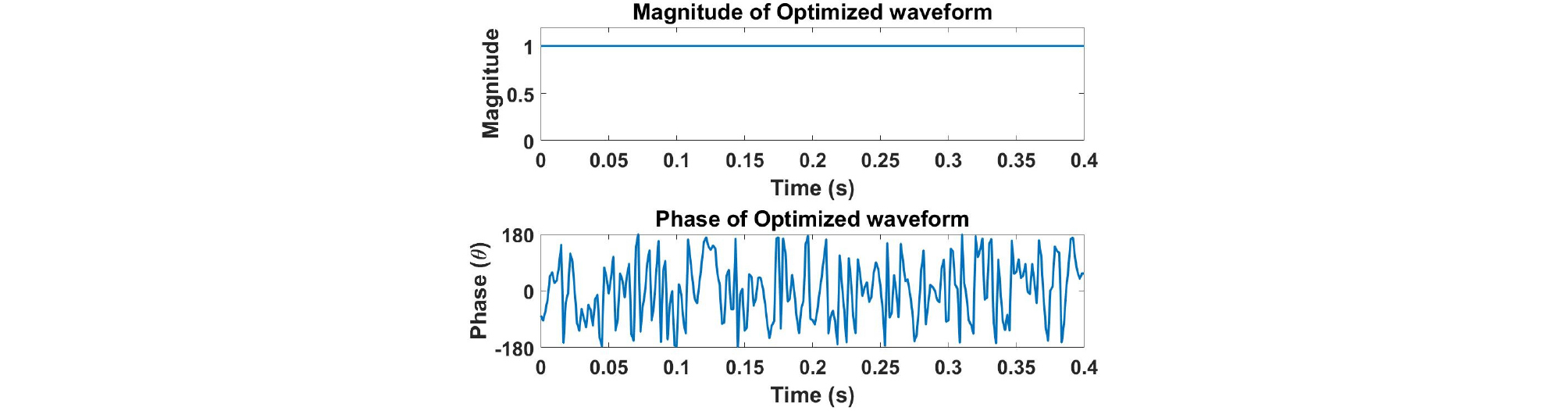
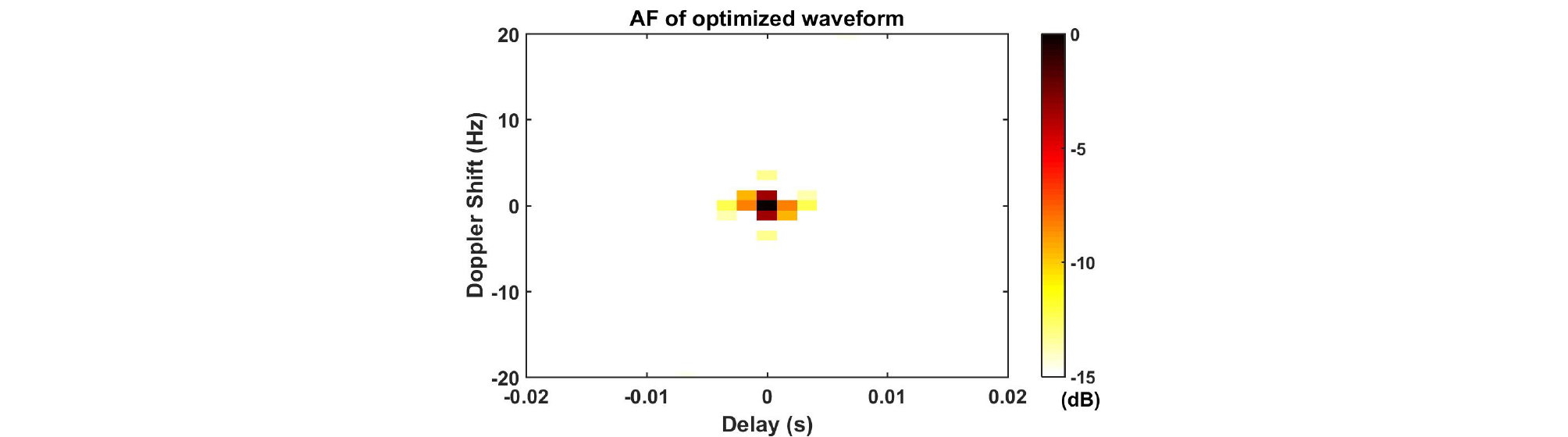
설계한 송신파형의 시간과 주파수 영역 그림은 Figs. 7, 8과 같고, 신호의 절대값 크기와 위상을 나타낸 그림은 Fig. 9, 모호함수를 확대한 그림은 Fig. 10과 같다. 모호함수를 통해 시간지연-도플러의 간섭성이 초기신호에 비해 낮아진 것을 알 수 있다. 그리고 설계한 송신파형을 이용하여 생성한 센싱행렬 A의 상호간섭성 값은 0.43으로 초기신호보다 매우 낮아졌다.
설계한 송신파형 의 스펙트럼에서 시스템이 원하지 않는 주파수 밴드가 얼마나 억압되어 있는지 비교하기 위해 평균 억압밴드 파워()라는 개념을 기준으로 설정하였다. 을 계산하는 과정은 다음과 같다. 를 의 점 FFT한 결과로 둔다. 그리고 주파수 밴드파워를 비교하기 쉽도록 하기 위해 를 통과 주파수 밴드의 의 평균값이 1이 될 수 있도록 정규화한다.[3]그러면 을 다음과 같이 계산할 수 있다.
Fig. 4와 Fig. 8에서 보여주는 LFM과 설계한 송신파형 스펙트럼의 은 각각 -14.29 dB, -22.9 dB이다.
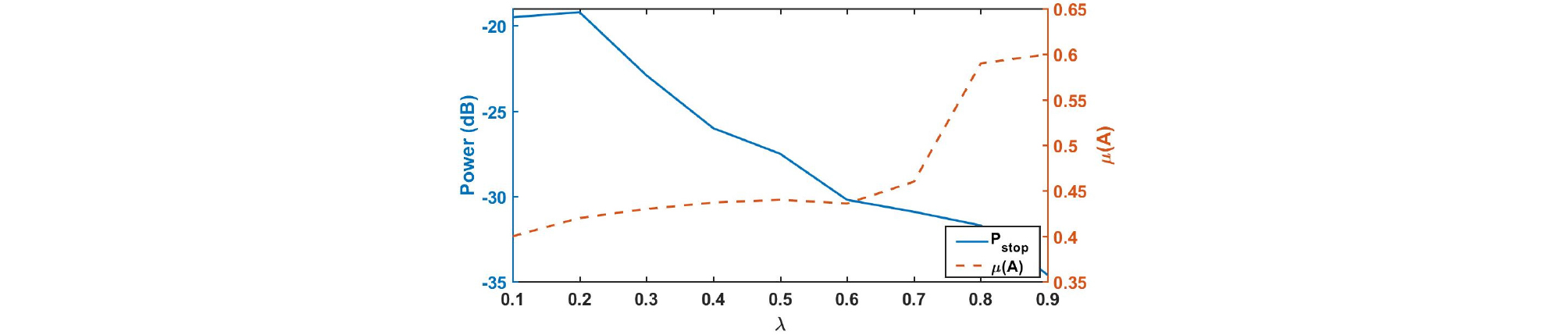
가중치 값에 따라 설계한 송신파형의 와 가 어떻게 영향을 받는지 살펴보기 위해서 나머지 조건은 고정시키고, 를 0.1부터 0.9까지 증가시키면서 과 상호간섭성 결과 값들을 Fig. 11에 표시하였다. Fig. 11를 통해서 이 클수록 주파수 밴드에 더 가중치를 주기 때문에 이 낮아지는 대신에 상호간섭성 값이 증가하는 경향을 볼 수 있다.
를 0으로 설정하여 대역폭 조건을 제외하고, 상호간섭성을 낮추는 방법만을 이용하여 설계한 신호는 가 0.3으로 매우 낮다. 그러나 신호의 주파수 영역 그림 Fig. 12를 보면 원하는 대역폭인 400 Hz를 만족하지 않고 또한 5.8 dB로 매우 높다. 따라서 본 논문에서 제시한 대역폭과 상호간섭성 두 조건을 모두 고려한 방법은 대역통과필터를 사용하는 압축센싱 능동소나에서 효용성이 높다고 할 수 있다.
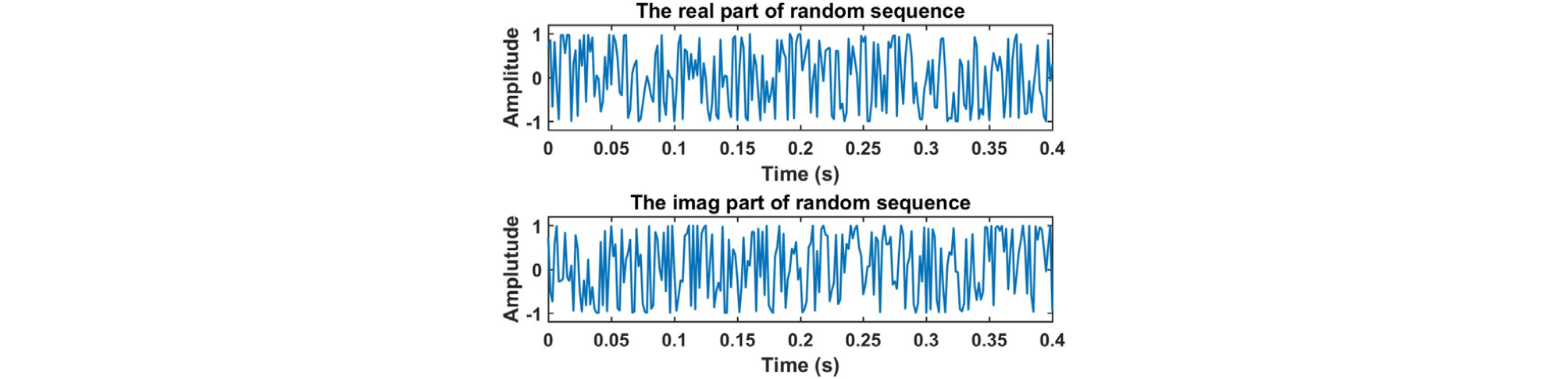
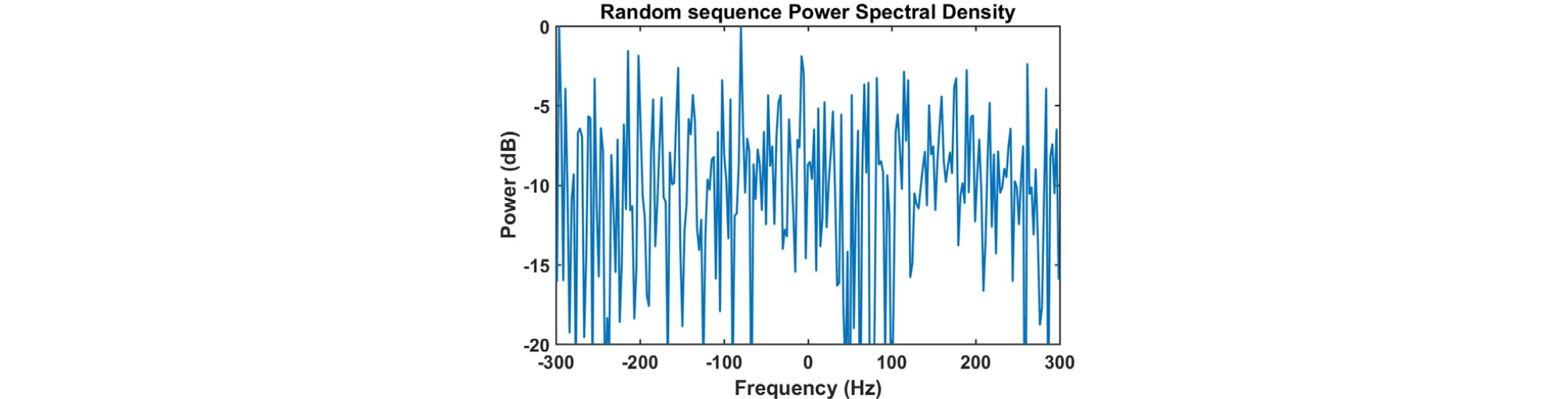
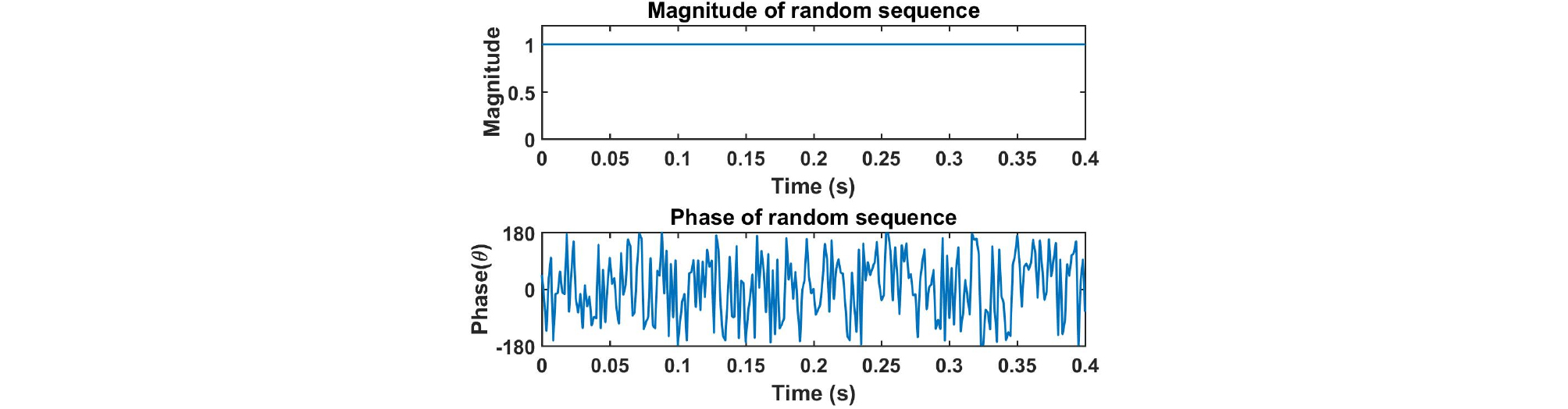
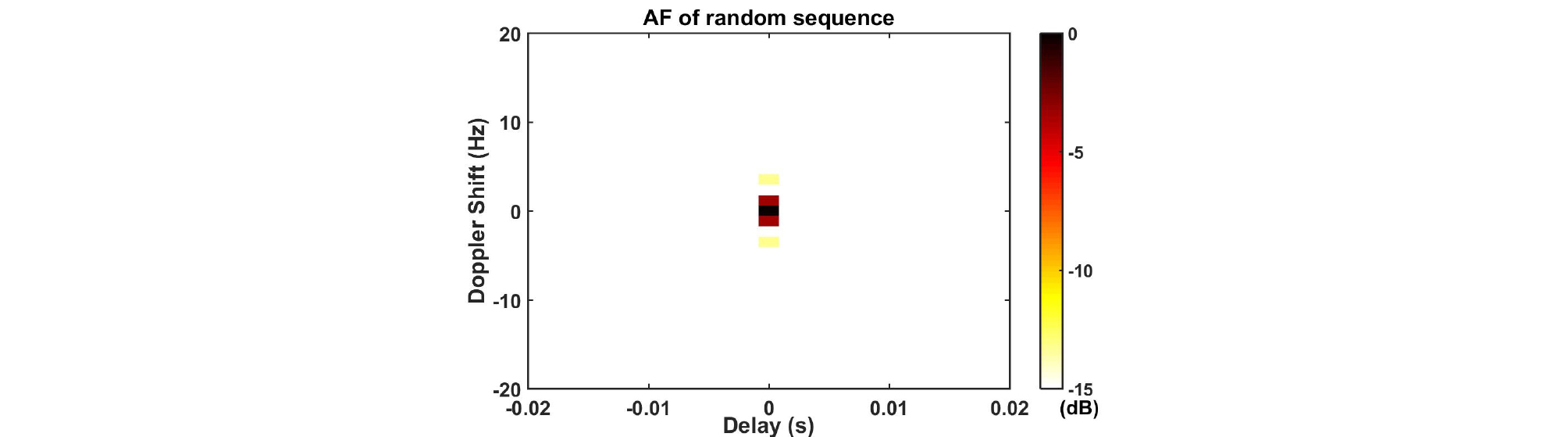
추가적으로 초기신호를 상호간섭성이 낮은 랜덤위상시퀀스로 설정하고, 다른 조건은 모두 동일하게 설정하여 모의실험을 진행하였다. 초기신호의 시간과 주파수 영역 그림은 Figs. 13과 14와 같고, 신호의 절댓값 크기와 위상을 나타낸 그림은 Fig. 15, 모호함수를 확대한 그림은 Fig. 16과 같다. 모호함수를 통해서 랜덤위상 시퀀스는 시간지연-도플러의 간섭성이 낮은 것을 알 수 있다. 그리고 랜덤위상 시퀀스를 이용하여 생성한 센싱행렬 A의 상호간섭성 값은 0.17이다. 그러나 주파수 영역 그림 Fig. 14를 보면 주파수가 원하는 대역폭인 400 Hz를 만족하지 않고 넓게 퍼져있는 것을 확인할 수 있다.
설계한 송신파형의 시간과 주파수 영역 그림은 Figs. 17, 18과 같고, 신호의 절대값 크기와 위상을 나타낸 그림은 Fig. 19, 모호함수를 확대한 그림은 Fig. 20과 같다. 모호함수를 통해 시간지연-도플러의 간섭성이 초기신호에 비해 높아진 것을 알 수 있다. 그리고 설계한 송신파형을 이용하여 생성한 센싱행렬 A의 상호간섭성 값은 0.38이다. 설계한 송신파형은 가 0.38으로 충분히 낮으면서 원하는 대역폭인 400 Hz를 만족한다. 따라서 본 논문에서 제시한 파형 설계방법은 초기신호를 상호간섭성이 낮은 신호로 설정하여도 적용 가능하다.
수신신호모델에서 표적의 거리-도플러 추정하기 위해 본 논문에서는 전통적인 방법인 정합필터와 압축센싱 기법 BPDN(CVX)를 사용하였다. 정합필터는 잡음이 추가된 수신신호 y와 송신신호 s의 복소공액 복사본과의 컨벌루션이며 신호 대 잡음비를 최대화한다. 반사계수 벡터 x를 구하기 위한 정합필터의 결과는 와 같다.[6] CVX 프로그램은 interior point method 알고리즘을 사용하여 BPDN 문제를 해결함으로써 희소한 반사계수 벡터 x를 구한다.[9]정합필터와 BPDN(CVX)를 이용하여 반사계수 벡터 x를 구하고, 반사계수 벡터에서 표적의 개수만큼 크기가 큰 값을 갖는 행들을 찾는다. 그리고 찾은 반사계수 벡터의 행들에 대응하는 센싱행렬 A의 열들을 통해 표적의 시간지연-도플러를 추정하였다.
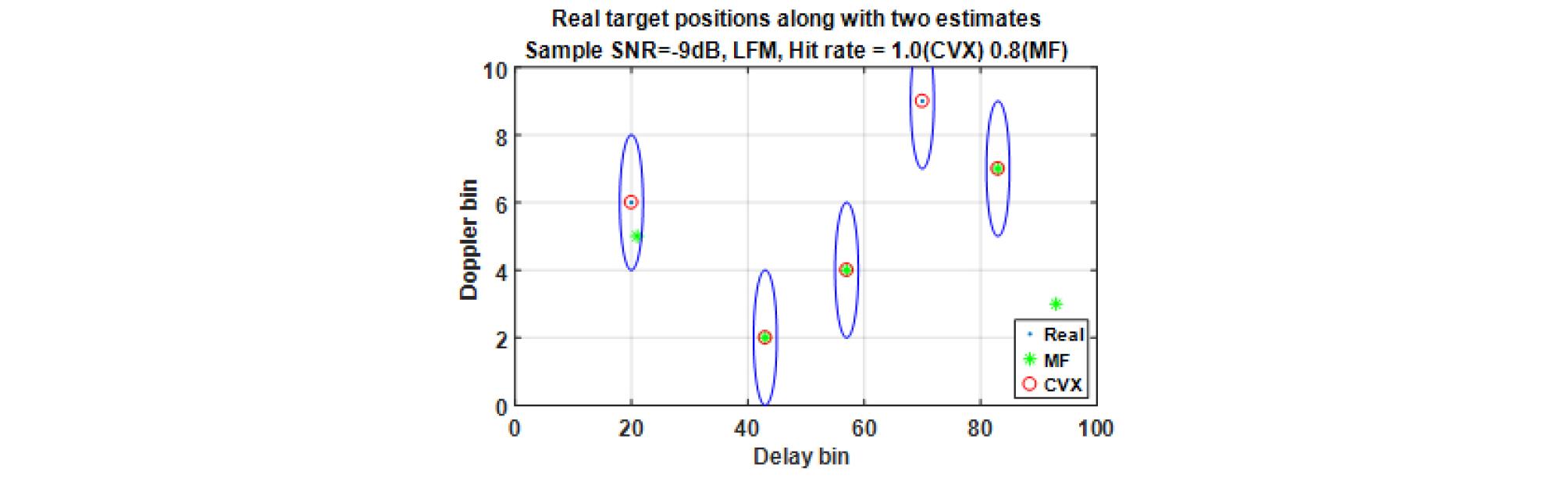
설계한 송신파형과 기존파형(LFM), 정합필터와 압축센싱기법(CVX)의 표적 탐지성능을 비교하기 위해 ‘성공비율’ 개념을 기준으로 설정하였다.[12]시간지연-도플러 평면상 실제 표적의 위치에서 일정한 크기의 타원 범위 안을 추정하면 탐지에 성공했다고 정의한다. 본 논문에서는 타원의 크기를 시간지연과 도플러 빈에 각각 ±2배로 설정하였다. 그리고 표적의 전체 개수와 성공한 개수의 비를 ‘성공비율’라고 한다. 모의실험에서 진행한 시간지연-도플러 평면의 크기는 100×10이고 표적의 개수는 5개로 설정하였다. 표적의 시간지연-도플러 평면상 위치와 추정결과 예시는 Fig. 21과 같다.
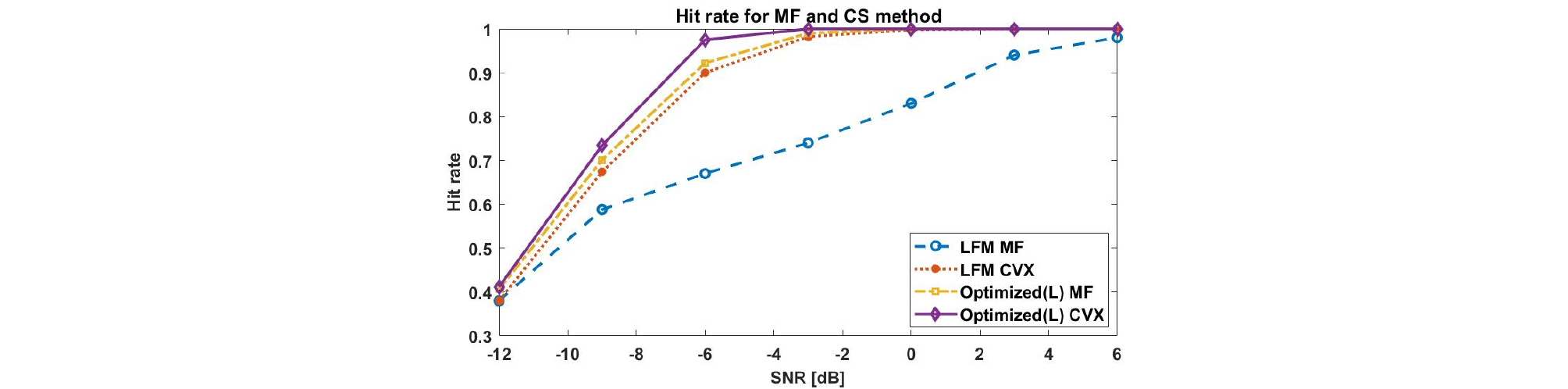
시간지연-도플러 평면의 크기가 100×10안에서 서로 다른 5개의 표적의 시간지연-도플러 추정하는 과정을 각각의 파형과 추정기법에 따라 신호 대 잡음비 별로 500번씩 반복 실험하여 성공비율의 평균값을 Fig. 22에 표시하였다. Fig. 22를 통해 기존신호(LFM)보다 설계한 신호의 성공비율이 높다는 것을 알 수 있고, 정합필터보다 압축센싱 기법(CVX)이 성공비율이 높다는 것을 알 수 있다. 전체적으로는 신호 대 잡음비가 낮아짐에 따라 성공비율도 낮아진다.