I. 서 론

발사체는 이륙 과정과 상승비행 과정 중에 집중적인 소음진동 환경에 노출되는데 이 과정이 탑재체(payload)가 수명주기 동안 겪는 가장 격심한 동적 환경에 해당하는 것으로 알려져 있다.^[1] 이륙 및 상승 과정에서 발생하는 소음진동은 발사체 외피에 랜덤 진동을 일으키고 다시 내부 공간으로 전파되어 민감한 전자장비나 탑재체의 고장을 유발하여 발사임무 실패의 결과를 초래하기도 한다.^[2,3,4] 발사체의 이륙 과정에는 2 Hz ~ 20 kHz 주파수 영역에 분포된 최대 170 dB ~ 200 dB 수준의 강한 소음이 근방영역에 발생하는데 로켓엔진에서 방출되는 뜨거운 초음속 제트와 주변 공기와의 난류 혼합이 소음의 주된 원인이며, 제트 유동과 주변 공기의 간섭으로 발생하는 충격파도 추가적인 소음을 발생시킨다.^[1]

발사체의 상승비행 중에는, 특별히 충격파/경계층 간섭이 발생하는 천음속 구간에서 난류 경계층(Turbulent Boundary Layer, TBL) 내부 섭동과 유동 박리, wake 효과, 돌출부 유동, 충격파 진동 등에 기인한 압력섭동으로 저주파(~60 Hz 이하)의 비정상(unsteady) 공력 하중이 가해지는 버핏현상이 발생한다.^[4,5,6] 1960년대 초반에 상승비행 중 천음속 구간에서 발생한 발사체의 연속적인 실패는 버핏현상에 기인한 것이었으며,^[4] 이를 계기로 발사체 구조설계 및 검증에 버핏하중을 반드시 고려하게 되었다. 발사체가 초음속에 도달하면 로켓 제트 소음에 비해 난류 유동에 기인한 소음이 지배적이게 된다.^[1]

발사체 탑재 화물의 질량과 크기가 지속적으로 증가함에 따라 대형의 탑재체를 수용하기 위해 탑재체 페어링의 직경이 발사체 상단 직경보다 더 큰 해머헤드(hammerhead)형 페어링을 사용하게 되었다. 해머헤드 형상의 불안정한 공력 특성으로 인해 형상 변화에 따른 공력 특성 및 동적 특성을 파악하기 위한 다수의 풍동시험들이 수행되었다.^[7,8,9]

발사체가 탑재체를 목표 궤도에 안전하게 투입하기 위해서는 이륙 및 상승비행 중 발생하는 소음진동 환경으로부터 탑재체를 보호하여야 하는데, 이를 위해서는 탑재공간에 작용하는 음향진동 하중의 저감 설계가 필요하다. 음향하중 저감을 위해서는 먼저, 1) 발사체에 작용하는 외부 음향하중을 예측하고, 2) 구조-음향 연성 해석을 통해 페어링 내부 음장을 분석하고, 3) 음장 특성에 맞는 흡차음재 설계를 통해 소음 레벨을 저감하는 절차를 거치게 된다. 따라서 첫 단계로 발사체에 작용하는 외부 음향하중 예측이 필요하다. 이륙 과정에서 발사체에 작용하는 소음진동 환경은 로켓 엔진의 초음속 제트가 화염유도로 및 발사대에 반사되어 형성되는데 이때 발생하는 소음 예측에 대한 연구는 Reference [10]에서 수행되었으므로 본 연구에서는 상승비행 중 음향하중을 연구 대상으로 하였다.

발사체 표면에 작용하는 음향하중은 준 경험적(semi-empirical) 방법 또는 수치적 방법으로 구해질 수 있다. 준 경험적 방법은 발사체 축소 모델의 풍동 시험이나 실물 발사체의 비행 시험에서 얻어진 데이터와 이론적 지식을 기반으로 도출된 모델 식을 이용하여 음향하중을 예측하는 방법이다. 고속 비행체 표면의 유동 특성은 비행체 형상과 비행 속도 등의 영향을 받고, 이에 따라 경계층 내의 압력섭동에 기인하는 음향하중도 달라진다. 1950년대 후반부터 많은 연구자들이 난류 경계층 내의 벽면 압력섭동에 관한 연구를 수행하여 다양한 예측 모델을 제시하였다. 대표적으로 Lowson,^[11] Robertson,^[12] Corcos,^[13] Efimtsov^[14]등의 모델이 있으며, 그 외에도 많은 연구자들에 의해 다양한 모델들이 개발되었다.^[15] 최근에는 기존 압력섭동 예측 모델을 대와류모사법(large eddy simulation) 및 직접모사법(direct numerical simulation)으로 얻은 결과와 비교 분석하여 각 모델의 특성과 상대적 정확도를 평가하는 연구도 수행되었다.^[16]

벽면 압력섭동에 대한 준 경험적 예측 모델에는 난류 경계층 내 압력섭동 에너지 강도를 제곱평균 압력섭동($\overline{p{\text{'}}^2}$)으로 나타내는 모델과 압력섭동 에너지의 주파수 분포를 나타내는 단일지점 주파수 스펙트럼 모델(파워스펙트럼 모델), 압력섭동 에너지의 파수 분포를 나타내는 파수-주파수 스펙트럼 모델로 구분된다. Cockburn과 Robertson^[17]은 Atlas-Agena 발사체의 15° cone-cylinder 형상 페어링에 대해 파워스펙트럼 모델을 적용하여 비행 중 음향진동 환경을 예측하였으며, 보다 최근에는 Yang과 Wilby^[18]가 준 경험식을 이용하여 Ares I-X 발사체의 비행 중 외부 음향진동 환경을 예측하였다.

파워스펙트럼 모델에서는 경계층 두께(boundary layer thickness, $\delta$), 경계층 배제두께(displacement thickness, ${\delta }^{*}$), 경계층 가장자리 속도($U_e$), 동압(dynamic pressure) 외에도 모델에 따라 다양한 유동장 파라미터가 입력 변수로 필요한데, 이런 값들은 모델링을 통해 예측하거나 실험을 통해 측정되어야 한다.

수치적 방법은 Direct Numerical Simulation(DNS), Large Eddy Simulation(LES), Detached Eddy simulation (DES) 등의 비정상 전산유체해법을 이용하여 시간에 따른 비행체 표면의 압력 섭동을 직접 계산하는 방법이다. 고 레이놀즈수에서 발사체 벽면 근처의 비정상 난류 경계층을 분해하기 위해서는 매우 많은 수의 계산격자가 필요하며, 따라서 현대의 대용량 병렬 연산 능력을 고려하더라도 여전히 많은 계산 시간과 비용이 소요된다는 단점이 있다.

본 연구에서는 비행 중 발사체 표면에 작용하는 음향하중을 준 경험식을 이용하여 구하였는데 이 때 준 경험식에서 필요로 하는 $\delta$, ${\delta }^{*}$, $U_e$ 등의 정보는 발사체 주변 유동장에 대한 정상상태 레이놀즈 평균 나비에-스토크스(Reynolds-Averaged Navier-Stokes, RANS) 방정식의 해에서 얻은 값을 사용하였다. 이와 같이 RANS 해석으로 얻은 경계층 정보를 준 경험식에 적용하여 난류 경계층 내부 압력섭동을 예측하는 방법은 Panda^[19]에 의해 제안되었는데, 이 방법은 경험적 예측기법의 간편성과 수치적 예측기법의 범용성을 동시에 갖는 장점이 있다. Park et al.^[20]은 이 방법으로 여러 연구자들에 의해 제안된 다양한 준 경험식 모델을 고속 비행체 형상에 적용하여 모델 간 압력섭동 예측 결과를 비교하였는데 각 연구자들이 제시한 모델 식은 사용되는 변수와 보정 계수 등에 차이가 있고 그에 따라 특징을 달리하기 때문에 예측 결과 또한 차이를 보임을 확인하였다.

발사체에 작용하는 외부 음향하중이 정의되면 페이로드 페어링(Payload Fairing, PLF) 구조물을 고려한 구조-음향 연성 해석을 통해 페어링 내부 음장을 분석한다. 본 연구에서는 잘 알려진 진동-음향 해석 프로그램인 VA One을 사용하였다.

발사체의 이륙 및 상승비행 중에는 넓은 주파수 대역에 분포된 음향하중을 받는데, 이러한 조건에서 위성체 구조물이나 탑재물이 받는 가속도를 올바르게 평가하기 위해서는 모든 주파수 대역의 압력 섭동을 응답 해석에서 고려하여야 한다. 이를 위해서는 응답 해석을 위한 모델링에서 시스템 구성 요소들의 모드 밀도(modal density)에 따라 다른 해석 방법을 적용해야 한다.

구조물의 음향-진동 해석에는 유한요소법(Finite Elements Method, FEM)이나 경계요소법(Boundary Element Method, BEM)과 같은 결정론적 방법과 통계적 에너지 분석법(Statistical Energy Analysis, SEA)이 흔히 사용된다. SEA는 해석 구조물을 에너지를 저장, 전달, 소산시킬 수 있는 여러 개의 연결된 하부 구조로 나누고 정상상태에서 각 하부 구조에 유입 및 유출되는 파워가 같다는 에너지 평형 원리를 적용하여 각 하부 구조간의 에너지 교환 과정을 해석함으로서 외부 입력에 대한 응답을 예측하는 방식이다.

모드 밀도가 낮은 저 주파수에서는 FEM이나 BEM으로 음향-진동 응답을 정확하게 해석할 수 있지만 모드 밀도가 높은 고주파 영역에서는 짧은 파장의 응답을 결정론적으로 표현하기 위해 필요한 시스템의 자유도가 비현실적으로 증가할 뿐만 아니라, 고차 모드에서 경계조건이나 해석대상의 작은 변화에도 모드 민감도가 증가하여 불확실성이 커지는 문제가 있다. 따라서 고주파수 대역에는 구조물의 모드와 주파수에 대한 평균적인 진동 응답을 예측하는 SEA 기법이 더 적합하다. 그러나 SEA 기법은 복잡한 실제 형상을 단순화하여 표현하는 기법의 특성으로 인해 실제 구조물의 특정 지점에서의 응답을 알 수 없고, 낮은 모드 밀도의 강성 구조체를 정확히 해석하지 못하는 단점이 있다. 이와 같은 이유로 중주파수 대역에서 하나의 시스템에 FEM과 SEA를 각기 다른 파트에 적용하여 연성 해석하는 FE-SEA 하이브리드 기법이 개발되었다. 이 기법은 SEA가 해석하지 못하는 강성의 영향을 받는 부분을 FEM으로 모드 해석을 수행하여 그 결과를 유한요소 하부시스템과 통계적 하부시스템 사이의 연결부에 적용함으로써 중주파수 대역에서 신뢰성 있는 결과를 얻을 수 있도록 하였다.

본 연구에서는 발사체 페어링에 대한 음향-진동 연계 해석에 있어 저주파수 대역에서는 FE, 중주파수 대역은 FE-SEA 하이브리드, 고주파수 대역에서는 SEA 기법을 사용하였다. 확립된 해석 기법을 이용해 음향-진동 연계 모델을 생성하고 이를 이용하여 페어링 내부 소음 레벨을 예측하였다.

Bianco et al.^[21]은 FE-SEA 하이브리드법을 이용하여 외부 음향하중에 의해 Vega-C 발사체 페어링 내부 탑재물에 가해지는 가속도를 계산하였다.

일반적으로 페어링의 차음만으로는 위성체나 탑재물에 허용되는 음향하중 수준을 초과하므로 음향제어 기구를 사용하는 것이 필요하다. 발사체 페어링에 적용되는 대표적인 음향제어 기구는 음향 블랭킷과 헬름홀츠 음향 공명기이다.^[22] 페어링 외피에 의한 차음 성능을 먼저 확인하고 필요에 따라 추가적인 흡음을 위한 음향 블랭킷과 헬름홀츠 공명기를 적용하여 음향제어 성능을 확인하였다.

발사체 페어링 내부에 탑재되는 위성이나 탑재물을 허용 가능한 가속도 환경 이내로 보호하기 위해서는 앞서 살펴본 바와 같이 발사체에 작용하는 외부 음향하중을 예측하여 구조-음향 연성 해석을 통해 페어링 내부 소음진동 환경을 분석하고, 허용 환경 규격 이내가 되도록 소음 레벨 저감 설계를 하는 과정이 필요하다. 이러한 각각의 과정들에 대해서는 많은 연구가 수행되었으나 전체 과정에 대한 시스템적 통합 연구의 케이스는 드물다.

본 연구에서는 정상상태 RANS 유동해석 결과와 압력섭동 준 경험식을 이용하여 발사체의 비행 중 외부 음향하중을 예측하고 FE-SEA 하이브리드 음향-진동 연성 해석 과정에 음향 블랭킷 및 헬름홀츠 공명기를 사용한 음향제어를 통해 탑재물의 안정성을 확보하는 설계/해석 프로세스를 개발하였다.

II. 본 론

2.1 음향하중 예측

2.1.1 준 경험적 예측 모델

본 연구에서는 Robertson^[12]의 난류 경계층 내부 압력섭동 파워스펙트럼 모델을 이용하여 발사체 페어링을 포함한 동체 표면에 작용하는 외부 음향하중을 예측하였다. Robertson은 경계층의 특성에 따라 1) 부착경계층 영역, 2) 박리유동 영역(압축 코너 및 팽창 코너), 3) 충격파 진동 영역으로 구분하고 각 영역에 대해 다음과 같은 압력섭동 파워스펙트럼 경험식을 제안하였다.

1) 부착경계층 영역

2) 박리유동 영역

3) 충격파 진동 영역

발사체 형상에서 일반적으로 충격파 진동에 의해 가장 강한 수준의 압력섭동이 발생한다. 이 영역에서는 충격파의 저주파 대역 에너지와 박리유동의 고주파 대역 에너지가 합해진 형태로 표시된다.

여기서 하첨자 $usw$(upstream of shock wave)는 충격파 전방지점을 의미한다. 제곱평균 압력섭동은 압력섭동 파워스펙트럼을 적분하여 구해진다.

2.1.2 정상상태 RANS 유동해석

난류 경계층 내부 압력섭동 파워스펙트럼 모델[Eqs. (1) ~ (3)]에 필요한 경계층 두께, 경계층 배제두께, 경계층 가장자리 속도 등의 값을 구하기 위해 발사체 주변 유동장에 대한 정상상태 RANS 해석을 수행한다. 본 연구의 해석 대상은 Coe와 Nute^[7]에 의해 마하수 0.60 ~ 1.17의 천음속 비행 조건에서 풍동시험 결과가 보고된 해머헤드형 페어링을 갖는 발사체이다. 발사체의 형상은 Fig. 1과 같으며, 페이로드 페어링은 전방 구형 원추체 후방에 각각 20° 경사와 6.5° 경사의 1차/2차 절두체(frustum)가 이어지고, 그 후방 실린더부에 이어 34° 경사의 보트 테일을 갖는 형상이다.

Fig. 1.

(Color available online) Hammerhead launch vehicle.

계산 조건은 마하수 M = 0.81, 받음각 0°, 레이놀즈수 4×10⁶/foot이며, 이때의 자유류 조건은 $p_{\infty }=$ 62448 Pa, ${\rho }_{\infty }=$ 0.8278 kg/m³, $T_{\infty }=$ = 262.8 K로 계산하였다. 계산 격자는 축대칭 발사체의 원주 방향으로 180° 부분만 형성하였고, 해당 경계면에는 대칭 경계조건을 적용하였다. 계산 격자의 원방 경계가 유동장에 미치는 영향을 최소화하기 원방 경계는 로켓 길이의 50배로 잡았으며 제한된 개수의 격자를 효율적으로 사용하기 위해 점성 경계층의 영향이 지배적인 벽면 경계층 영역과 비행체에서 비교적 벗어난 원방 영역의 두 개 영역으로 나누어 계산격자를 형성하였다. 이와 같이 형성된 격자는 Fig. 2과 같으며, 총 격자수는 약 5.1×${10}^6$개이다. 로켓 벽면에서 첫 번째 격자까지의 거리는 $y^{+}<1$이 되도록 $1\times {10}^{-4}$ inch로 주었으며, 벽면 근처에는 인플레이션 층으로 격자를 형성하여 경계층 해석이 용이하도록 하였다.

Fig. 2.

3D mesh used for RANS simulation.

유동해석에는 범용 유동해석 소프트웨어인 ANSYS Fluent 19.2의 압력 기반 해법을 사용하였는데 압력-속도의 연계는 압력 기반의 연속방정식을 모멘텀 방정식과 동시에 풀이하는 coupled scheme을 사용하였으며, 난류 모델로는 $k-\omega$ SST 모델^[23]을 사용하였다. 공간차분화는 압력 방정식에 대해서는 2차 정확도를 사용하였고, 밀도, 운동량, 에너지, 난류 방정식에 대해서는 2차 upwind 스킴을 사용하였다. 시간 전진은 pseudo-transient 법을 사용하였다.

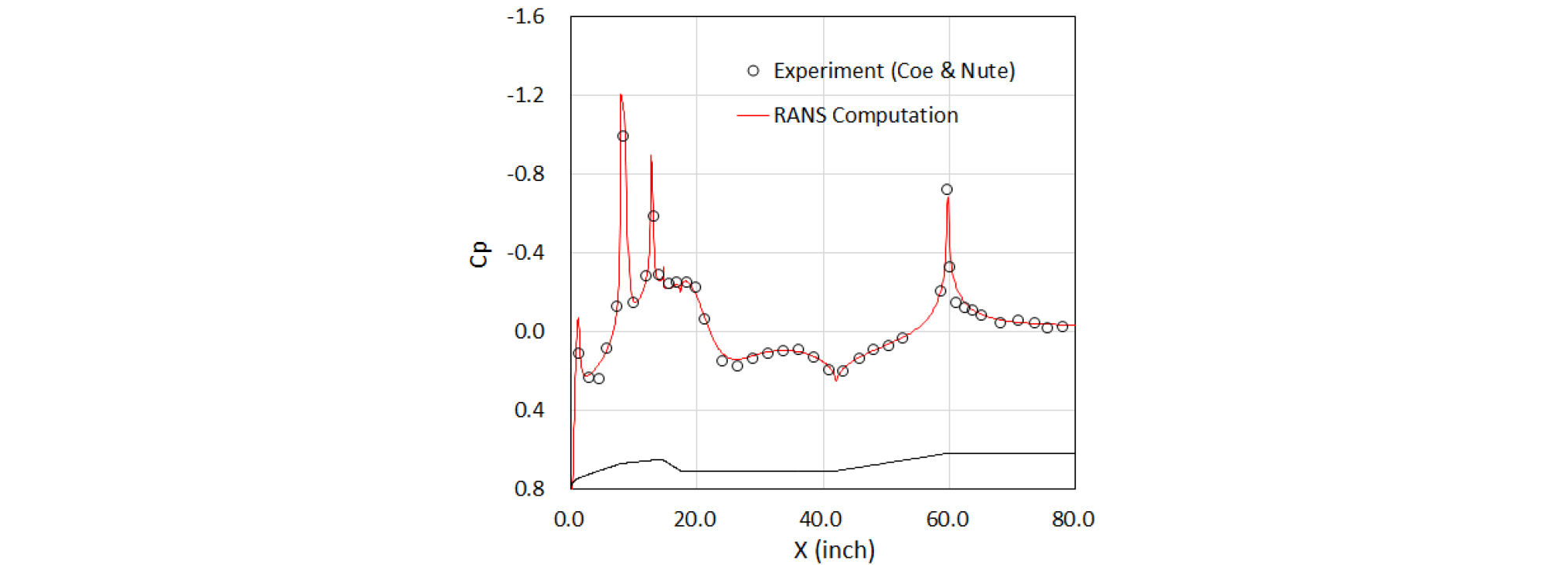
경계조건은 벽면에는 단열, 점착조건, 유입류 원방 경계에는 pressure-far-field 조건, 유출류 원방 경계에는 pressure-outlet 조건을 적용하였다. 원방 경계에서의 난류 조건은 난류 강도 0.2 %, 난류 점성비 2의 값을 사용하였다. 해석을 통해 얻은 발사체 동체 표면의 압력 분포과 대칭면에서의 마하수 분포를 Fig. 3에 나타내었다. 또한 동체 표면에서의 압력계수 분포를 Fig. 4에 나타내었는데 해석 결과는 실험값과 잘 일치함을 알 수 있다. 페이로드 페어링(Fig. 1)의 선단 구형 원추와 1차 절두체와의 접점부, 1차/2차 절두체의 접점부, 2차 절두체와 실린더부와의 접점부, 그리고 발사체 1단/2단 어댑터와 발사체 1단의 접점부 모서리는 팽창유동이 발생하는 영역으로 압력계수에 음(negative)의 피크가 나타나 있는데, 이 현상은 Fig. 5의 동체 표면 압력선도에서도 동일하게 관찰된다.

Fig. 3.

(Color available online) Pressure and Mach number contour plot.

Fig. 4.

(Color available online) Comparison of Cp distribution.

Fig. 5.

(Color available online) Expansion-shockwave and shock-induced boundary layer separation (Exp: expansion, S: shock).

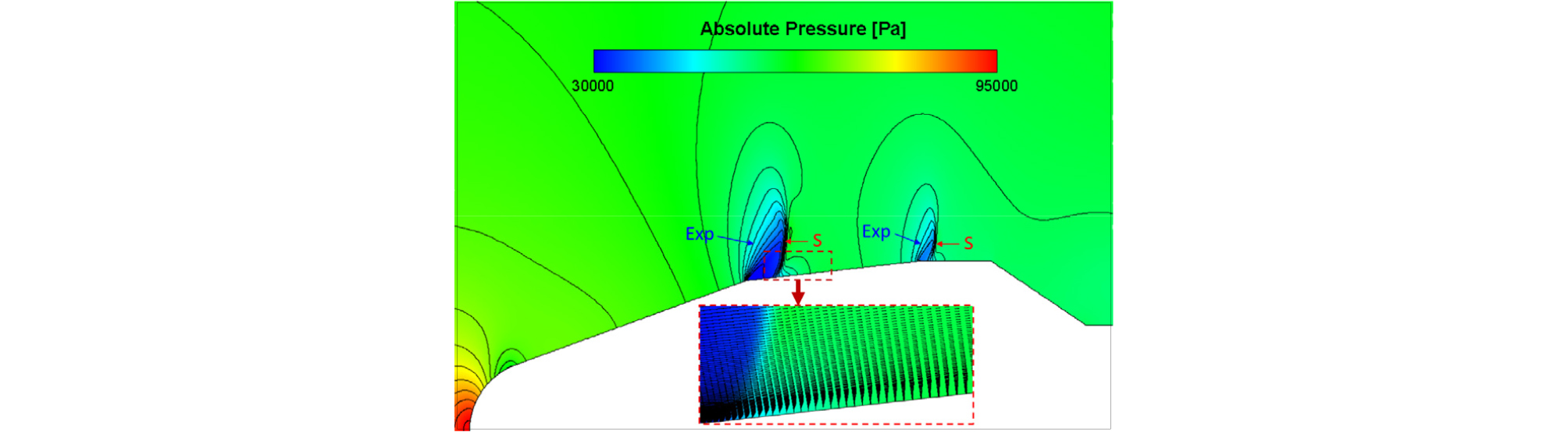
Fig. 3의 마하선도로부터 1차/2차 절두체 접점부와 2차 절두체와 실린더부 접점부 모서리에서 유동 팽창에 의해 마하수가 음속을 돌파하여 초음속 유동이 형성되고 그 직후에 수직에 가까운 충격파가 형성되어 있음을 알 수 있다. 이 영역을 보다 자세히 관찰하기 위해 해당 영역을 확대하여 Fig. 5에 나타내었는데 충격파/경계층 간섭에 의해 유동박리가 발생하였음을 속도 벡터를 통해 확인할 수 있다. 또한 Fig. 3의 마하선도로부터 페어링 어깨에서 유동박리가 일어나고, 박리된 유동은 후방의 2단 동체에 재부착되고 있음을 알 수 있다.

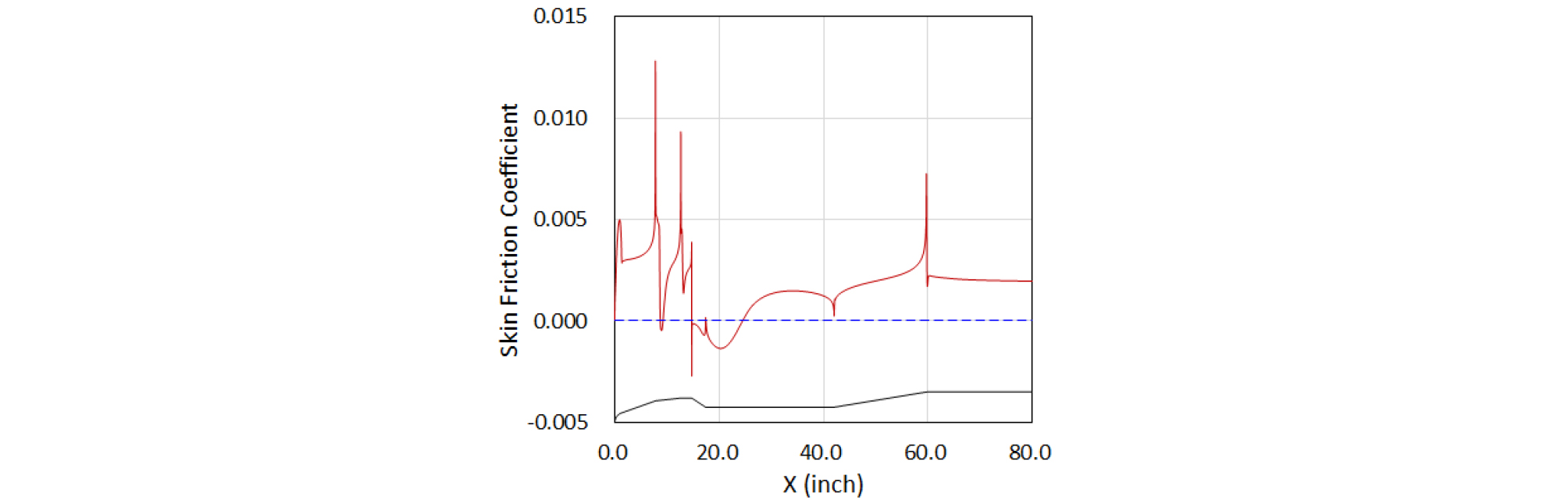
유동박리 영역을 보다 엄밀하게 확인하기 위해 벽면 마찰계수($C_f$)를 Fig. 6에 나타내었는데 1차/2차 절두체 접점부의 후방에 음의 값을 갖는 박리영역이 짧게 나타나고 있으며, 앞서 마하수 선도에서 보였던 페어링 어깨에서의 유동 박리와 후방 재부착 지점의 위치가 확인이 가능하다.

Fig. 6.

(Color available online) Skin friction coefficient distribution.

이들 팽창유동 발생 지점과 박리유동의 재부착 지점은 비정상 압력섭동이 크게 나타나는 영역으로 알려져 있으며, 이어서 살펴볼 준 경험식을 이용한 압력섭동 예측 결과에서도 이런 경향이 확인되고 있다.

RANS 해석 결과로부터 압력섭동 예측 모델 경험식의 파라미터인 경계층 두께와 배제두께, 경계층 가장자리에서의 마하수를 구하기 위해 비행체 표면에 수직인 지점들에서 표면에 평행한 속도와 전압력 등의 유동 프로파일을 추출하여 이들 파라미터를 계산하였다.

2.1.3 음향하중 예측

Cockburn과 Roberson^[17]은 발사체 선두부의 대표적인 세 가지 형상(cone-cylinder, cone-cylinder-flare, cone- cylinder-boattail)에 대해 아음속-천음속-초음속 비행 시에 나타나는 기본적인 유동 패턴을 정의하였다. 본 연구의 대상인 해머헤드 형상의 경우 Fig. 7에 도시한 바와 같이 천음속 비행 시 페어링 cone 부위에서 부착유동을 유지하다가 실린더 부위에서 유동 팽창으로 유속이 초음속에 도달하고 이에 따라 그 직후방에 수직에 가까운 충격파가 형성되며, 충격파 입사 후방 경계층 내부 유동은 충격파의 강도에 따라 유동 박리가 발생할 수 있다고 설명하였다. 이 때 난류 경계층 섭동의 영향으로 충격파 진동 현상이 나타나며 페어링 어깨에서 박리된 유동은 박리 지점 근방 또는 유동 재부착 지점에 약한 충격파를 형성할 수 있다고 설명하였다. 또한 Yang과 Wilby^[18]은 팽창 코너에서 유동이 가속되면서 팽창 팬을 형성하고 그 이후에 자유류의 속도로 빠르게 감속하면서 부착충격파를 형성하는데 이 충격파 지점에서 압력섭동이 매우 크게 나타난다고 설명하였다.

Fig. 7.

Characteristics flow features on cone-cylinder- boattail launch vehicle fairing geometry at transonic speed.^[15]

해머헤드 발사체에 대한 정상상태 RANS 유동 해석 결과는 이러한 경험적 유동 패턴과 잘 일치하는 결과를 보여주었다. 발사체 주변 유동은 난류 경계층 내부 압력섭동 특성에 따라 부착경계층, 압축 코너, 팽창 코너, 충격파 진동 영역으로 구분할 수 있는데 앞서 살펴본 천음속에서 해머헤드형 발사체에 대한 경험적 유동 패턴 및 RANS 해석 결과에 따라 해석 대상 발사체를 Fig. 8과 같이 총 14개의 유동 영역으로 구분하고, Table 1에 나타낸 것과 같이 각 영역에 해당하는 유동특성을 지정하였다.

Fig. 8.

(Color available online) Division of zones for semi-empirical fluctuating pressure prediction.

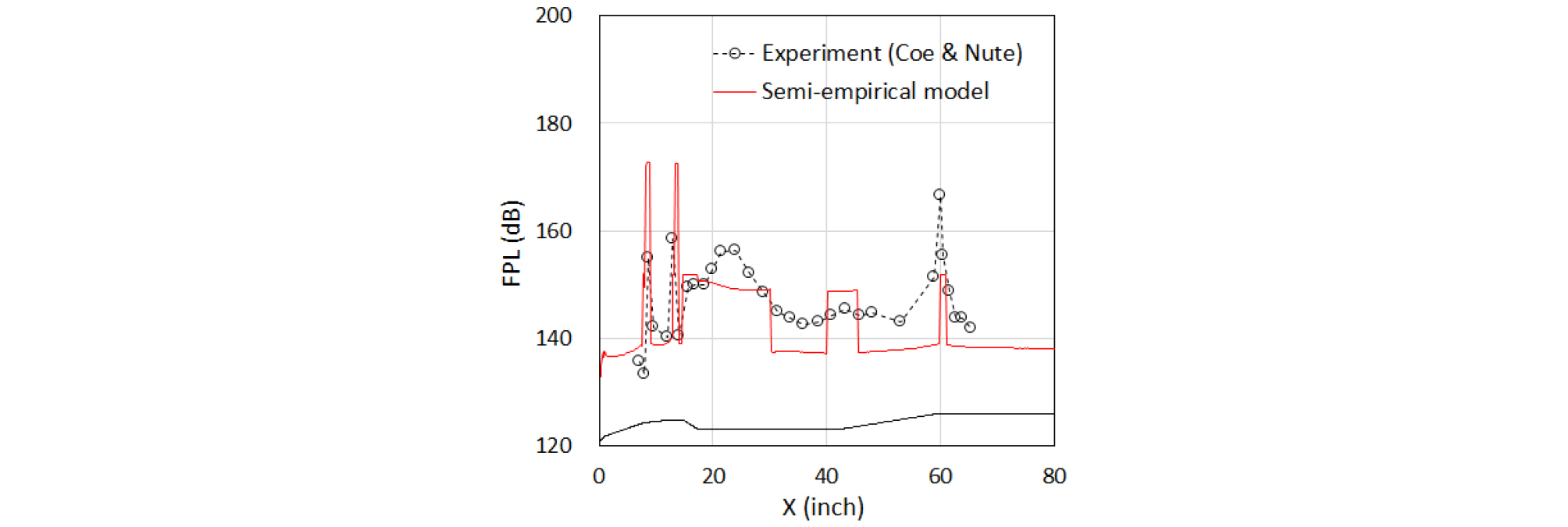
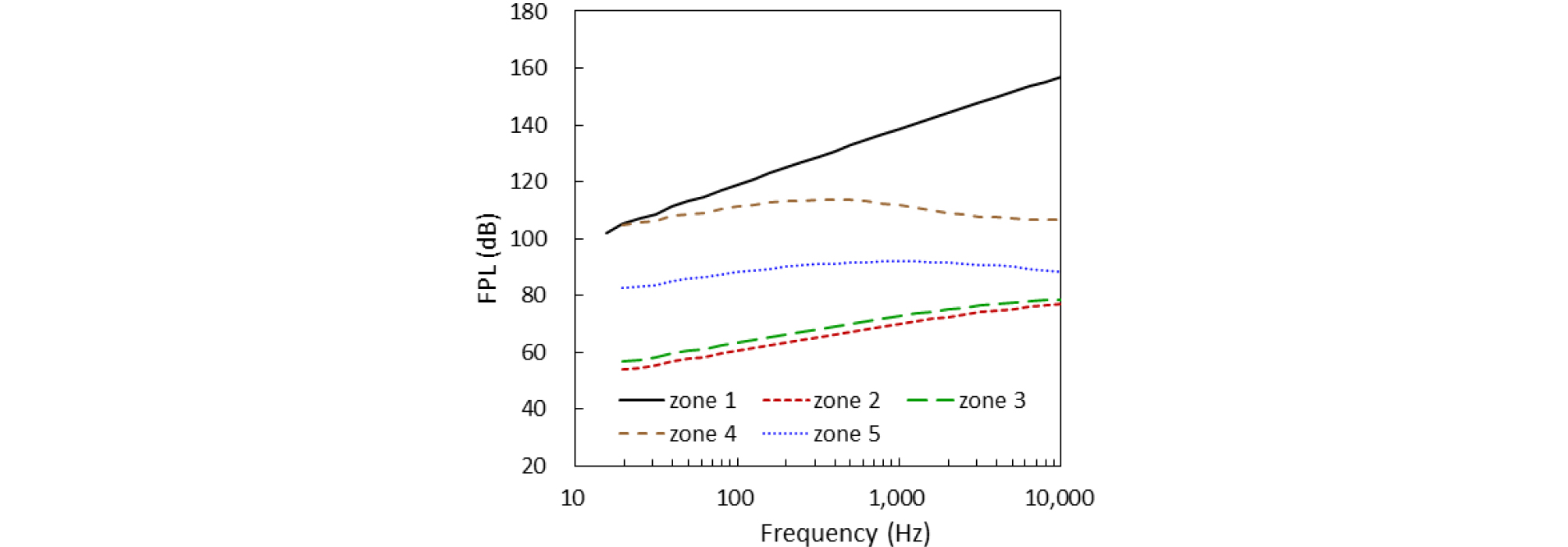
본 연구에서 사용한 Robertson의 파워스펙트럼 모델에서는 압축 코너와 팽창 코너를 박리유동 영역으로 분류하고 동일한 형태의 예측식을 적용한다. 따라서 부착경계층 영역에는 (1)식, 압축 코너와 팽창 코너에는 (2)식, 충격파 진동 영역에는 (3)식을 적용하여 압력섭동레벨(Fluctuating Pressure Level, FPL)을 예측하고, 그 결과를 Fig. 9에 나타내었다. FPL은 다음과 같이 정의된다.

전체적으로 박리유동 영역의 음향하중이 증가하였으며 충격파 영역에서 큰 값을 가졌다. 이러한 경향은 Coe와 Nute^[7]의 실험 결과와 동일하다. 또한 해머해드 페어링의 경우 보트 테일에서 시작되는 전단층(shear layer) 하부 재순환 영역의 난류 구조에 의해 큰 압력섭동이 발생하는데 해당 영역에 박리유동 영역 모델을 적용한 결과 음향하중이 급격히 증가하여 실험 결과와 비슷한 경향을 보이는 것을 확인할 수 있었다.

Fig. 9.

(Color available online) Comparison of predicted acoustic load by semi-empirical model with experiment.

2.2 구조-음향 연성 해석

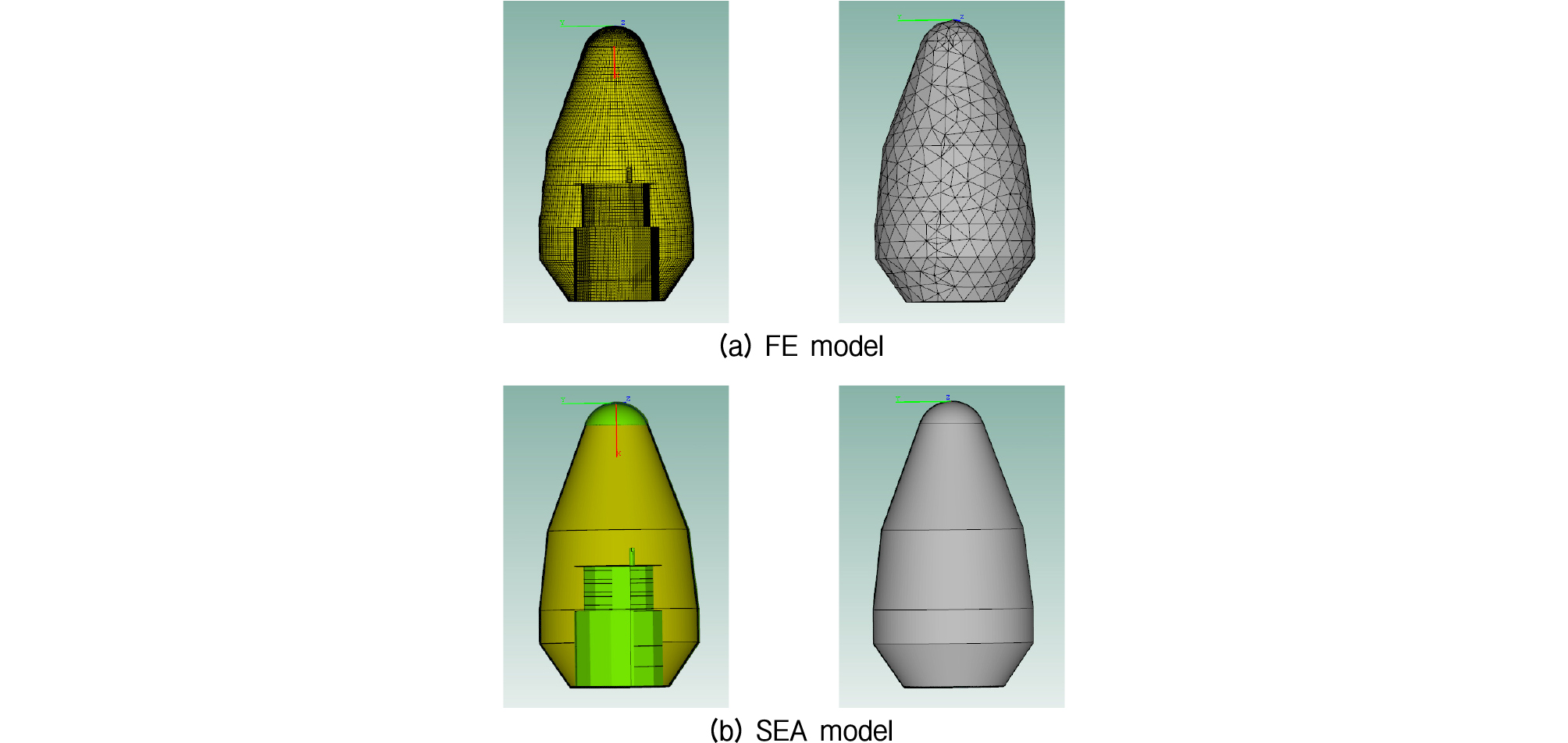
발사체 페어링에 대한 구조-음향 연성해석을 위해 치수를 갖는 실제 페이로드 형상이 정의되어야 한다. 본 연구는 발사체 탑재부의 음향하중 저감을 위한 설계/해석 프로세스 개발이 주목적이므로 외부 음향하중 해석에 이용하였던 페어링과 동일한 형상을 갖는 가상의 페어링을 형성하였다. 페어링의 최대 직경은 2.87 m, 길이는 5.2 m이다. 페어링 내부 탑재물은 KSR-III^[24] 과학탑재부를 간략화하여 모델링하였다. 일반적으로 발사체 페어링은 굽힘 강성과 무게 대비 강도 비율이 우수한 복합재 샌드위치 재료로 제작되며 본 연구에서도 카본 에폭시 면재와 알루미늄 허니콤 코어의 조합으로 이루어진 복합재 페어링 모델을 구성하고, FE-SEA 하이브리드 기법으로 구조-음향 연성해석을 수행하였다.

2.2.1 FE-SEA 하이브리드 해석

구조물의 진동해석에서 저주파 대역에서는 모드가 명확하게 구분이 되어 FEM이나 BEM으로 해석이 용이하지만 가진 주파수 영역이 넓어지면 공진 모드의 수가 많아지고 경계조건이나 구조물의 작은 변화에도 모드가 민감하게 변화해서 이들 방법을 사용하기 어렵다. 이러한 결정론적 방법은 일반적으로 저주파 대역에서 사용되고 고주파수 영역에서는 통계적 방법인 SEA 기법을 사용하게 된다.

실제 해석 대상체는 해석 주파수 대역의 파장에 비해 크기가 큰 시스템과 작은 시스템을 모두 가지고 있기 때문에 중주파수 대역에서는 유한요소법과 통계적 에너지 해석법을 결합한 하이브리드 방식의 해석이 필요하다. 이 방식은 SEA 기법을 기반으로 하여 강성이 큰 부분은 모드 밀도가 작으므로 FE 하부시스템으로 모델링하는 방식이다. SEA 하부시스템과 FE 하부시스템의 junction을 통한 에너지 전달 관련된 응답을 하이브리드로 모델링 가능하다. FE- SEA 하이브리드 해석을 통해 FE 모드 정보가 반영된 연성 손실계수를 적용하여 더 넓은 주파수 대역에서 소음진동 해석이 가능하다.

2.2.2 FE-SEA 하이브리드 해석 모델

(1) 외부가진 하중

외부가진 하중은 앞서 기술한 준 경험적 압력섭동 파워스펙트럼 모델로 계산된 값을 VA One의 (Turbulent Boundary Layer, TBL) 가진 방법으로 주었다. VA One에는 Efimtsov^[14]의 압력섭동 파워스펙트럼 모델이 내장되어 있으나 특정 모델에 종속되지 않고 다양한 외부하중 모델을 사용할 수 있도록 외부에서 계산된 값을 불러들여 적용하는 방법을 사용하였다.

TBL 압력섭동에 대한 구조물의 응답은 압력섭동의 공간 상관관계에 크게 의존하는데 이것을 정확하게 정의하는 데는 어려움이 있다. VA One에서 두 지점 $\mathit{x}(x,y)$, $\mathit{x}\mathbf{\text{'}}(x\text{'},y\text{'})$ 사이의 협대역 공간 상관관계는 다음과 같이 정의된다.

여기서

$\frac{1}{d}=\sqrt{k_x^2+k_y^2+{\left(\frac{8}{3\delta }\right)}^2}$

이며, $\left|\Delta x\right|=|x\text{'}-x|$, $\left|\Delta y\right|=|y\text{'}-y|$는 각각 두 지점 간 유동 방향(along flow)과 유동 단면 방향(cross- flow)의 거리, $c_x$, $c_y$는 이들 각 방향의 공간상관 감쇠계수(spatial correlation decay coefficient), $U_0$와 $U_{\mathrm{c}}$는 각각 자유류의 속도와 난류 경계층 내 압력섭동이 전파되는 대류 속도이며, $\sigma =U_c/U_0$이다. 유동 방향과 유동 단면 방향으로의 파동수 $k_x$, $k_y$는 다음과 같이 정의된다.

본 연구에서는 이들 변수에 대해 다음과 같이 주어지는 VA One의 기본 설정값을 사용하였다.

TBL 가진을 주기 위해 페어링을 5개의 구역으로 나누고 이들 각 영역에 대해 압력섭동 파워스펙트럼을 계산하여 그 결과를 Fig. 10에 나타내었다.

Fig. 10.

(Color available online) Predicted fluctuating pressure power spectral density on payload fairing.

(2) 구조 및 음향 모델링

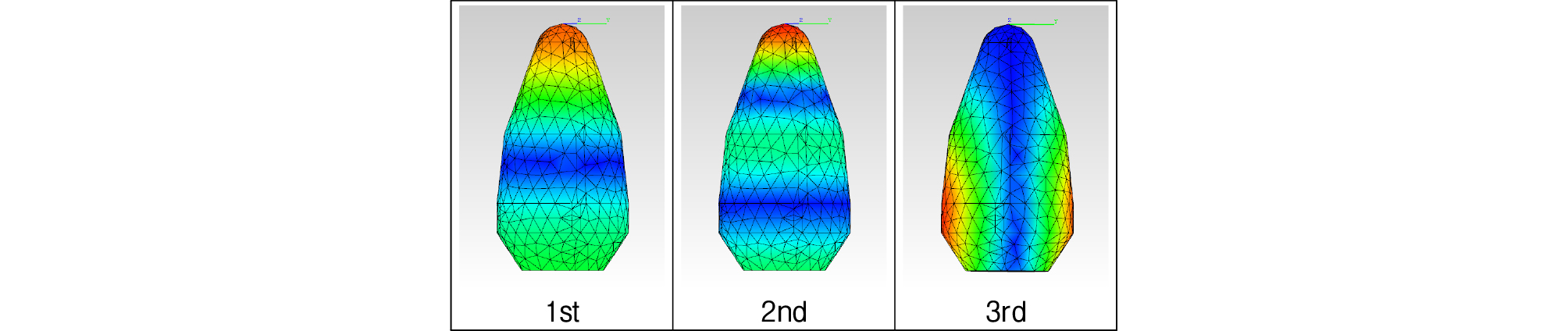
발사체 경계층 내부 압력 섭동의 주파수 대역이 광범위하므로 각 주파수 대역에 적합한 해석기법을 적용하였다. 25 Hz ~ 200 Hz 주파수 대역에서는 FE, 200 Hz ~ 500 Hz 대역은 FE-SEA 하이브리드, 500 Hz ~ 10 kHz 대역은 SEA 해석 모델을 사용하였다. FE와 FE-SEA 하이브리드 해석을 위한 구조 모드 해석은 페어링 스킨 구조 형상의 쉘(shell) 모델을 이용하여 상용 소프트웨어인 ANSYS APDL 19.2로 계산하였다. 이때 페어링 하단 부에는 fixed 경계조건을 적용하였다. 모드 해석 결과를 VA One SEA에서 불러들여 사용하였다. FE 모델에서 필요한 음향 모드 해석은 VA One SEA 내부의 Acoustic FE 모듈을 사용하였다. Fig. 11과 Fig. 12는 각각 페어링의 구조 모드 형상과 음향 모드 형상을 보여준다.

Fig. 11.

(Color available online) Structural mode shapes of the PLF.

Fig. 12.

(Color available online) Acoustic mode shapes of the PLF.

하이브리드 해석 모델링에서 페어링 내부 탑재물은 하부시스템의 사이즈가 작아 모드 밀도가 낮아서 FE로 모델링하였고, 페어링 외피도 헬름홀츠 공명기의 적용을 위해 크기가 작게 나누어져 있어 모드 밀도가 낮기 때문에 FE로 모델링하였다. 페어링 내부 음향 공간은 음향하중 저감을 위해 설치하는 흡차음재가 공기 기인(air-borne) 소음에 미치는 영향이 크므로 SEA 캐비티(cavity)로 설정하였다. 페어링과 내부 캐비티 사이의 에너지 정보 전달을 위해 면연결(area junction)을 적용하였으며, 외부 음장 환경을 반영하는 Semi-Infinite Fluid(SIF)를 페어링 외피의 구조 하부 시스템에 연결하였다. 계산에 사용된 FE 해석모델과 SEA 해석모델을 Fig. 13에 나타내었다. FE/ FE- SEA/SEA 해석의 모든 주파수 대역에서 댐핑 손실계수는 프로그램의 기본값인 1 %를 적용하였다.

Fig. 13.

(Color available online) FE and SEA models (left: structure model, right: acoustic model).

2.3 음향하중 저감 설계

발사체 페어링 내의 음향하중 저감을 위해 일반적으로 사용되는 음향 블랭킷은 400 Hz 이상의 주파수 대역에 유효하며,^[22] 이보다 낮은 저주파 대역에서는 음향(헬름홀츠) 공명기가 주로 사용된다. 음향 공명기는 공동(cavity)과 좁은 면적의 목으로 구성되는 음향기구로서 Fig. 14에 그 전형적인 형상을 나타내었다. 음향 공명기는 공명 주파수에서 높은 흡음 성능을 가지며, 흡음은 공명기 목 부근에서의 점성 마찰에 의한 에너지 소산, 열전도 등에 의한 에너지 손실에 의해 일어난다.

Fig. 14.

(Color available online) Schematic of Helmholtz resonator.

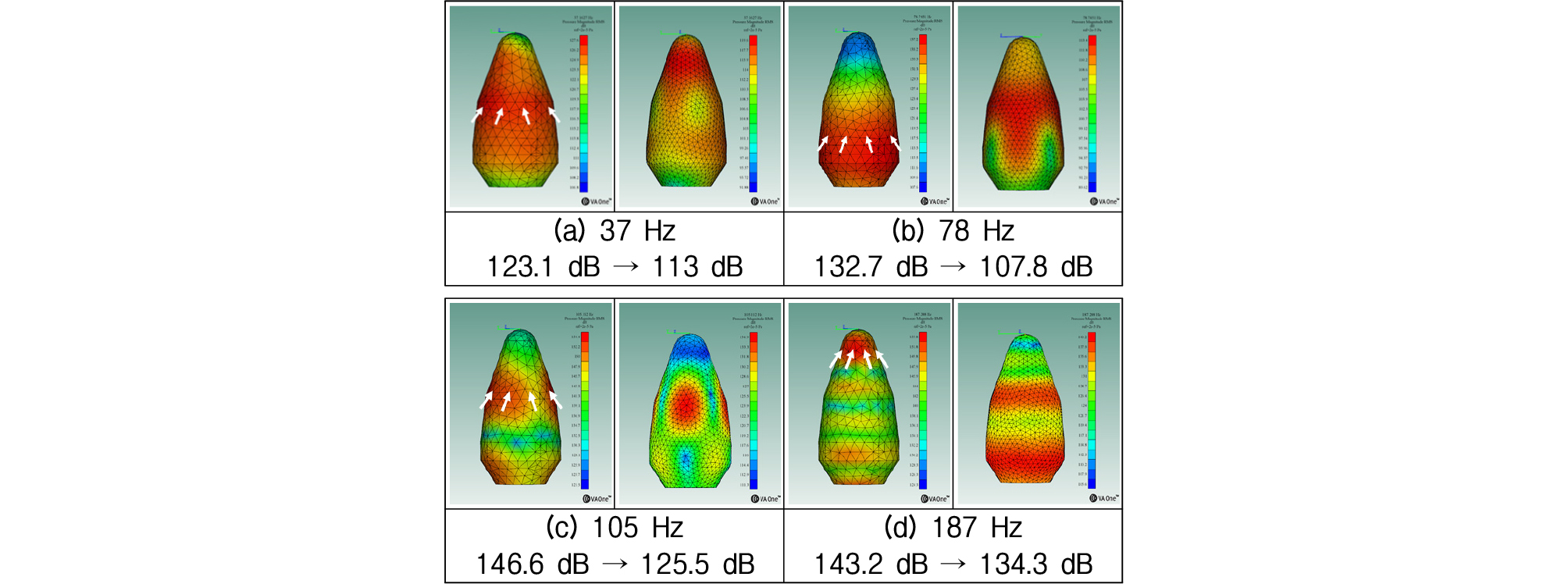
먼저 음향 공명기에 의한 흡음 효과를 확인하기 위해 페어링 내부 음향 모드 해석 결과에서의 고유 주파수와 주파수 대역별 내부 음압 레벨(Sound Pressure Level, SPL)을 바탕으로 총 4개의 타깃 주파수(37 Hz, 78 Hz, 105 Hz, 187 Hz)를 선정하여 이들에 대한 임피던스 값을 구하였다. 임피던스($Z_R$) 계산에 사용된 모델은 다음과 같다.

여기서 $\rho$는 매질의 밀도, $\omega$는 각 주파수, $k$는 파수, $\nu$는 동점성 계수, $c$는 음속이며, $V$와 $S$는 각각 공명기 캐비티의 체적과 목의 면적, $l$, $a$는 각각 목의 길이와 반지름이다. 헬름홀츠 공명기를 음압(sound pressure)이 크게 작용하는 위치에 90° 간격으로 4개의 쉘 요소를 하나의 공명기로 가정하여 계산된 임피던스 값을 부여하였다.

음향 공명기가 커버하지 못하는 고 주파수 대역의 흡음을 위하여 공명기가 부착되지 않은 영역에 멜라민 폼(이하 ML 폼) 소재의 음향 블랭킷을 부착하는 것으로 모델링하였다.

이와 같이 페어링 내부 표면에 다양한 조건으로 흡차음재를 부여하고 본 연구에서 개발된 FE-SEA 구조-음향 연성해석 모델을 이용해 흡차음재에 의한 페어링 내부 음장 변화 및 음향하중 저감 효과를 살펴보았다.

2.4 해석 결과

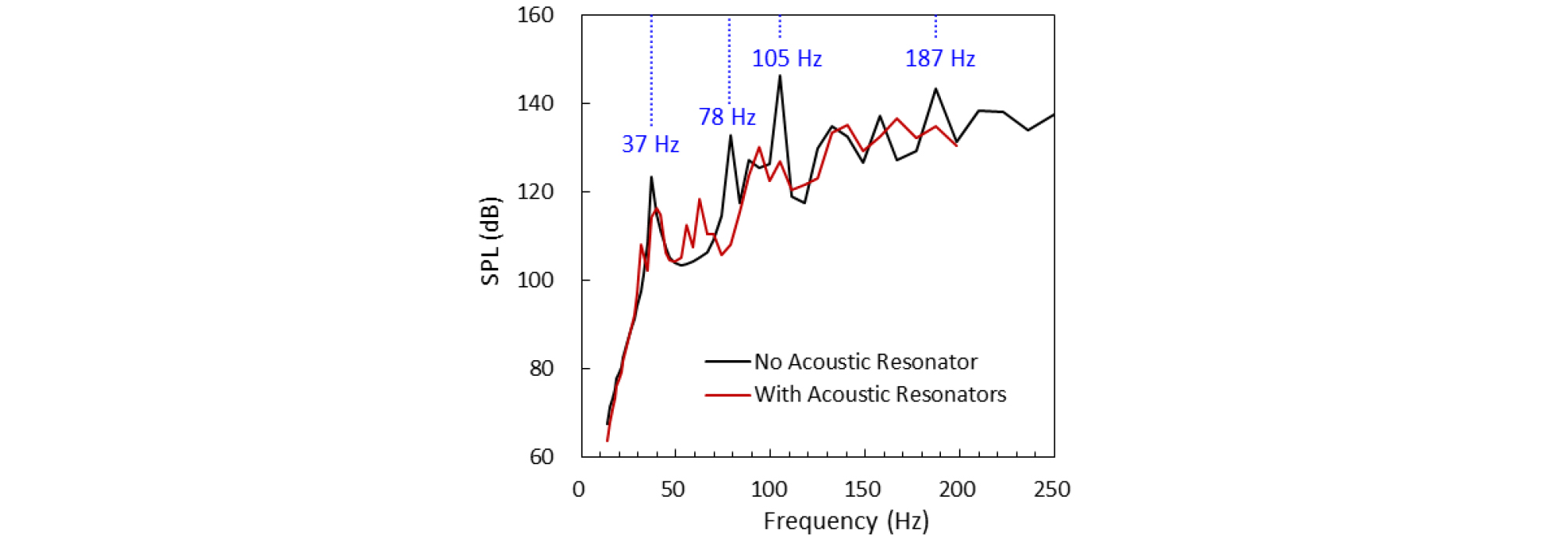
타깃 주파수의 음향 공명기 적용 시 FE 내부 음향 공간 표면에서의 음압 레벨(SPL)을 Fig. 15에 나타내었다. 음향 공명기 적용에 따른 페어링 내부 음장 변화를 Fig. 16에 나타내었는데 동조시킨 주파수 대역의 음압이 감소되었음을 알 수 있다. 이로부터 적절한 음향 공명기 타깃 주파수의 선택과 위치 설계를 통해 페어링 내부 음향진동 환경을 개선할 수 있음을 확인할 수 있었다.

Fig. 15.

(Color available online) Fairing inner surface SPL reduction at target frequency by Helmholtz resonator.

Fig. 16.

(Color available online) Fairing SPL with Helmholtz resonator.

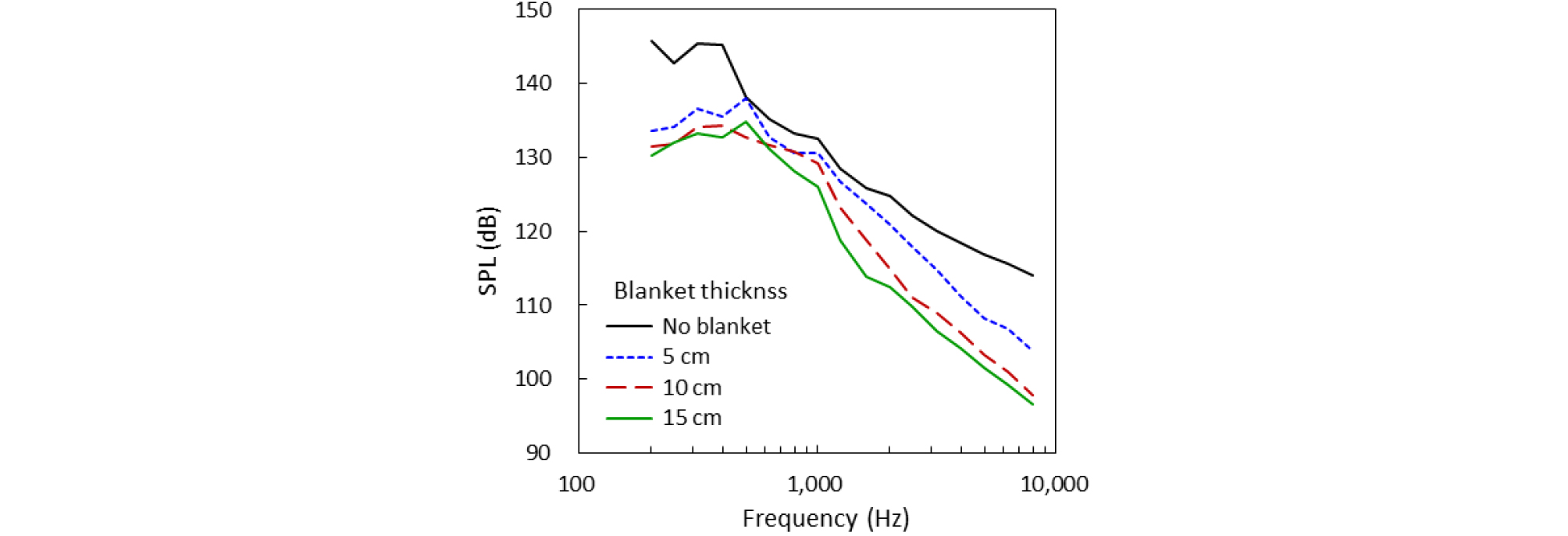
음향 블랭킷의 효과를 확인하기 위해 세 가지 두께(5 cm, 10 cm, 15 cm)의 ML 폼을 적용한 경우에 대한 페어링 내부 소음 레벨을 Fig. 17에 나타내었다. 모든 주파수 대역에서 흡음 효과를 확인할 수 있으며 고주파 대역으로 가면서 흡음효과는 상승하였다. 블랭킷 두께가 두꺼워질수록 흡음 효과는 증가하였으나 증가의 폭은 감소하였다. 두께 10 cm ML 폼의 무게는 33.7 kg으로 예측되는데 200 Hz ~ 10 kHz 대역에서 5 dB ~ 10 dB 수준의 소음저감 효과를 얻을 수 있으므로 이로 인한 탑재물의 구조 경량화로 훨씬 더 큰 중량 이득을 얻을 수 있다.

Fig. 17.

(Color available online) Fairing cavity SPL with different acoustic blanket thickness.

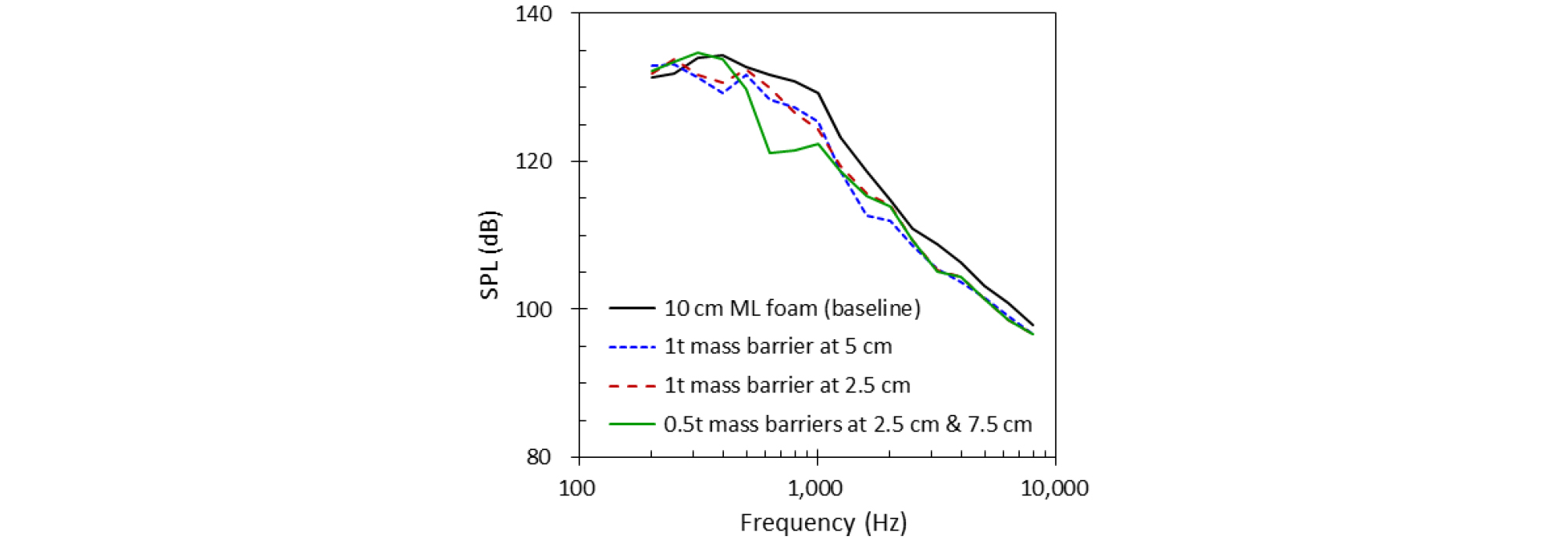
1990년대 후반에 200 Hz ~250 Hz 대역에서 최소 3 dB 이상의 페어링 내부 소음저감을 위한 음향 블랭킷 개발에서 유리 섬유 블랭킷 내부에 높은 밀도의 질량판을 삽입하여 소음저감 목표를 달성하였는데^[22,25] 본 연구에서도 그 효과를 확인해 보기 위한 해석을 수행하였다. 본 연구에서는 유리 에폭시 소재의 질량판을 ML 폼 내부의 다양한 위치에 삽입한 경우에 대한 해석을 수행하였다. 두께 10 cm의 ML 폼 내부에 두께 1 mm의 질량판이 삽입된 경우, 벽으로부터 2.5 cm 위치에 동일 질량판이 삽입된 경우, 그리고 벽으로부터 2.5 cm와 7.5 cm 위치에 두께 0.5 mm의 질량판이 각각 삽입된 경우에 대한 해석을 수행하여 그 결과를 Fig. 18에 나타내었다. 질량판이 삽입된 세 경우 모두 상당한 소음저감 효과가 있음을 확인할 수 있었다. 특히 600 Hz ~ 800 Hz 대역에서는 질량판이 없는 경우에 비해 10 dB 수준의 큰 소음저감 효과를 확인할 수 있었다. 또한 하나의 질량판보다 1/2 두께의 질량판을 서로 다른 위치에 삽입하는 경우가 600 Hz ~ 1,200 Hz 대역에서 소음저감 효과가 더 뛰어난 것으로 나타났다.

Fig. 18.

(Color available online) Fairing SPL with different mass barriers.

이상에서 살펴본 바와 같이 본 연구에서는 발사체의 탑재물에 작용하는 음향하중 저감을 위한 설계/해석 통합 프로세스를 개발하고 그 절차에 따라 음향하중을 예측하고 적절한 소음저감 기구를 설계하여 발사체 페어링 내 탑재 공간에서의 소음저감 효과를 평가해 봄으로써 개발된 프로세스의 타당성을 확인하였다.

III. 결 론

본 연구에서는 정상상태 RANS 유동해석 결과를 난류 경계층 내부 압력섭동 준 경험식에서 이용하여 발사체 외부 음향하중을 예측하고, FE-SEA 하이브리드 음향-진동 연성해석을 통해 발사체 페어링 내부 음압레벨을 예측한 다음, 음향 블랭킷과 헬름홀츠 공명기와 같은 수동제어기구로 음향하중 저감설계를 구현하는 프로세스를 개발하였다. 개발된 프로세스를 해머헤드형 발사체에 적용하여 페어링 내부 음향진동환경 개선 효과를 살펴보고 이를 통해 본 연구에서 개발된 절차의 타당성을 검토하였다.

연구 대상으로 선정한 발사체의 천음속 비행 조건에서 복합재 페어링 스킨만으로는 음향 모드 주파수 부근에서 적정 내부 소음 레벨을 초과하는 주파수 대역들이 존재하는 것으로 나타났다. 해당 주파수 대역에서의 흡음을 위해 표면 음압이 크게 나타나는 위치의 쉘 요소에 헬름홀츠 공명기를 임피던스 값으로 부여하여 타깃 주파수에서의 소음저감 효과를 확인하였다. 헬름홀츠 공명기의 효용성이 낮은 고주파수 영역에 대해서는 멜라민 소재의 음향 블랭킷을 적용하여 음향 블랭킷의 두께와 질량판의 유무에 따른 흡음 특성을 파악하였다. 음향 블랭킷을 적용한 결과 모든 주파수 대역에서의 흡음 효과를 확인할 수 있었으며, 블랭킷 두께 증가에 따른 흡음 효과 증가의 폭은 점차 감소하였다. 블랭킷 내부에 질량판을 삽입함으로써 적은 무게로도 큰 음향하중 저감 효과를 얻을 수 있었으며, 질량판을 서로 다른 위치에 나누어 삽입하는 것이 더 효과적인 것으로 나타났다.

본 연구에서 개발된 페어링 내부 음향하중 저감 설계/해석 절차는 순수하게 해석적인 방법으로 타당한 정확도 수준의 페어링 내부 음향환경 예측과 음향하중 저감 설계를 빠른 시간 내에 가능하게 하여 개발비용 절감에 기여할 수 있으므로 발사체 개발 초기단계에 유용하게 쓰일 수 있을 것으로 판단된다.