I. 서 론
II. 이 론
2.1 PD(Product Directivity) 모델
2.2 비선형 음향 모델
2.3 KZK 방정식의 기존 수치 해석 방법
III. 전기적 빔 조향 특성 예측을 위한 수치 해석 알고리즘 구현
3.1 수치 해석 알고리즘 개선 방법
3.2 전기적 빔 조향 특성 예측을 위한 초기 음압 경계 조건
IV. 수치 해석 결과 및 고찰
4.1 초기 음압 경계 조건 입력 결과
4.2 차주파수음 빔 조향 특성 수치 해석 결과
V. 결 론
I. 서 론
파라메트릭 어레이 현상은 강하게 발생된 서로 다른 두 가지 고주파수음 f1, f2이 매질의 비선형성을 통해 차주파수음 |f1, - f2,|에 해당하는 고지향성 저주파음을 간접적으로 발생시키는 것을 뜻한다. 이를 이용하면 발생된 차주파수음의 파장보다 작은 크기의 방사판으로 고지향성 특성을 확보할 수 있다.[1] 파라메트릭 어레이 현상의 이론적 해석은 1963년 Westervelt[1]에 의해 최초로 발표 되었다. 그 후, 1975년 Bennet와 Blackstock[2]에 의해 공기 중에서도 파라메트릭 어레이 현상이 구현 가능함이 발표되었다. 이러한 이론적 연구를 바탕으로 파라메트릭 어레이를 수중 통신, 고해상도 능동 소나, 고지향성 초음파 거리센서, 고지향성 라우드 스피커에 적용하기 위한 다양한 연구가 수행되었다.[3], [4], [5]
여러 분야에서 특수한 목적을 위해 사용되는 파라메트릭 어레이가 좀 더 유용한 기술이 되기 위해서는 고지향성 차주파수음 발생 방향을 조절할 수 있는 빔 조향 기술 적용이 필요하다. 파라메트릭 어레이의 빔 조향 기술 구현을 위해 실험적으로 다양한 연구가 진행 되었으며, 가장 손쉬운 방법으로 기계적으로 음원 트랜스듀서의 방향을 변화시키는 시스템이 Olszewski et al.[6]에 의해 보고되었다. 그러나 기계적인 빔 조향 시스템은 크기가 크며, 사용자가 원하는 조향 방향을 즉각적으로 반영할 수 없다는 한계점을 가지고 있다. 따라서 디지털 신호 처리를 통한 전기적 빔 조향 방법이 Gan et al.[7]에 의해 보고되었다. Gan은 고주파수음인 1차 음파에 전기적 빔 조향 조건을 적용하여 방향성을 조절하였으며, 이를 바탕으로 차주파수음의 조향이 가능함을 보였다. 이외에도 다수의 연구진들에 의해 전기적 조향 시스템을 이용하여 차주파수음 조향을 위한 연구가 수행되었다.[8], [9], [10]
이와 더불어 차주파수음 조향 특성을 예측하기 위한 이론적 연구도 진행 되었으며, 준선형 근사 조건(약한 비선형성)하에 가우시안 음원으로부터 발생되는 차주파수음 빔 패턴을 계산하는 방법이 Darvennes et al.[11], [12]에 의해 발표 되었다. 해당 연구에 따르면 원거리에서 나타나는 차주파수음 빔 패턴은 1차 음파의 방향성 곱으로 결정되며, 이러한 음파의 방향성 관계를 PD(Product Directivity) 모델이라 칭하였다. 이와 같이 PD 모델은 쉽고, 간단하게 차주파수음의 조향 특성을 계산할 수 있으므로 차주파수음 빔 패턴, 조향 특성 예측을 위해 사용되고 있다. 그러나 PD 모델로 차주파수음의 빔 패턴을 계산해 보면 주엽의 반치 빔폭이 실험으로 측정된 반치 빔폭에 비해 50 % ~ 80 % 수준으로 좁게 나타나는 결과를 볼 수 있다.[13], [14] 또한 PD 모델은 기본적으로 준선형 근사 조건을 필요로 하므로 강한 1차 음파, 그리고 이를 통해 발생되는 강한 차주파수음이 필요한 파라메트릭 어레이 음원(ex. 라우드 스피커, 고지향성 초음파 거리센서)의 조향 특성 예측에 적합하지 않다.
파라메트릭 어레이 빔 조향 시스템을 구현할 때 가장 중요한 부분은 사용자가 원하는 방향과 범위(빔 폭)만큼 정확하게 고지향정 저주파음을 보낼 수 있도록 설계하는 것이다. 이를 위해서는 준선형 근사 조건에 해당되지 않는 파라메트릭 어레이 음원에서도 차주파수음 조향 특성, 특히 주엽의 빔 폭을 정확하게 예측할 수 있는 이론적 방법 도출이 필요하다. 본 논문에서는 PD 모델의 한계를 극복하고 차주파수음의 조향 특성을 예측하기 위해 KZK 방정식(Khokhlov – Zabolotskaya – Kuzentsov)을 적용하였다. KZK 방정식은 닫힌 형태의 해가 존재하지 않으므로 Lee와 Hamilton, 또는 Cleveland[15], [16], [17]가 발표한 수치 해석 알고리즘을 사용하여 해를 도출해야 한다. 다만 기존에 공개된 수치 해석 알고리즘은 기본적으로 단일 채널에 동일한 음압 조건만 초기 조건으로 다룰 수 있도록 정의 되어 있다. 즉, 전기적 조향 시스템과 같은 복잡한 음압 조건 적용이 불가능 하다.[15], [16], [17] 따라서 먼저 다양한 초기 음압 경계 조건을 다룰 수 있도록 기존 수치 해석 알고리즘 개선을 진행 하였다. 그리고 이를 바탕으로 파라메트릭 어레이의 차주파수음 조향 특성을 수치 해석을 통해 도출 하였으며, 실험을 통해 측정된 조향 특성과 비교해 보았다. 그 결과, 개선된 KZK 방정식 수치 해석 알고리즘을 이용하면 PD 모델 적용 조건을 벗어나는 파라메트릭 어레이 음원에서도 차주파수음 조향 특성, 특히 정확한 주엽의 빔 폭 예측이 가능함이 확인되었다.
II. 이 론
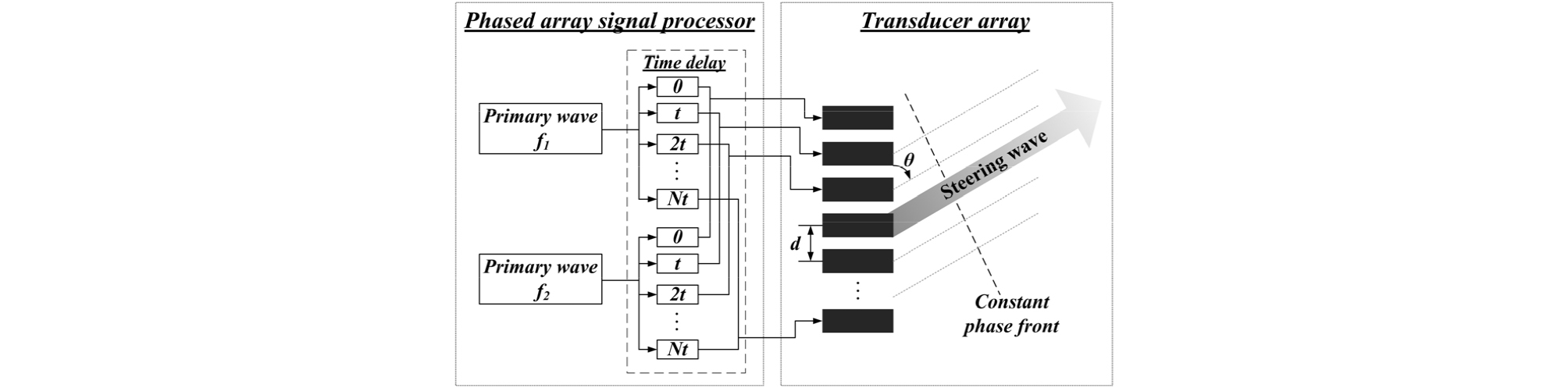
파라메트릭 어레이에 Fig. 1과 같은 전기적 조향 시스템을 적용하게 되면, 파라메트릭 어레이 라우드 스피커의 경우 고지향성 가청음 방향을 손쉽게 변경할 수 있으며, 파라메트릭 어레이 초음파 거리센서 시스템의 경우 기계적 움직임 없이도 원하는 방향의 거리를 측정하는 것이 가능하다. 따라서 파라메트릭 어레이가 적용된 응용 분야의 활용도를 확장시키기 위해서는 차주파수음 방향성을 조절하는 것이 필수적이다. 또한 파라메트릭 어레이 빔 조향 기술을 다양한 응용 분야에 적용, 직접적으로 사용하기 위해서는 차주파수음 빔 조향 특성을 이론적으로 예측하는 과정도 매우 중요하다.
2.1 PD(Product Directivity) 모델
서론에서 언급하였듯이, PD 모델은 준선형 조건하에 가우시안 음원에서 발생하는 차주파수음의 원 거리 빔 패턴을 1차 음파의 방향성 곱으로 계산하는 방법이다. 이를 식으로 표현하면 Eqs. (1)과 (2)와 같다.[10], [13]
| $$D_d=D_{f_1}(\theta)D_{f_2}(\theta),$$ | (1) |
| $$D_{f_n}(\theta)=\exp\lbrack-\frac14(ka)^2\tan^2\theta\rbrack,$$ | (2) |
여기서 θ는 음파의 진행 방향으로부터 떨어진 각도, k는 파수, a는 방사판의 반경이다. Eq. (1)에서 알 수 있듯이, PD 모델을 이용하면 비교적 간단하게 차주파수음의 빔 패턴, Dd을 계산해 낼 수 있다. 그러나 준선형 근사 조건하에 PD 모델을 적용하기 위해서는 큰 열점성 감쇠 효과로 비선형 상호 작용 영역이 1차 음파의 근거리 음장 영역 내에 존재해야 하며 (비선형 감쇠 계수, A ≥ 1), 유한 진폭 효과는 상대적으로 약해야한다(Gol'dberg number, Γ ≤ 1).[18] 또한 PD 모델은 1차 음파의 방향성 곱으로 차주파수음의 빔 패턴을 계산해 보면 주엽의 빔 폭이 측정 결과보다 다소 좁게 나타난다.[13], [14] 따라서 본 연구진은 PD 모델로 강한 차주파수음을 필요로 하는 다양한 응용 분야에서 빔 조향 특성을 정확히 예측하는데 한계가 있다고 판단하였다. 예를 들어 파라메트릭 어레이 초음파 거리센서의 빔 조향 현상을 실험적으로 구현한 논문의 경우, 강한 차주파수음을 발생시키기 위해 Table 1과 같은 음원 조건을 사용하였다.[19]
Table 1. Experimental condition.[19]
Table 1의 조건을 바탕으로 동일한 방사 영역을 가지는 음원을 가정하여[19] 비선형 감쇠 계수 (A) 와 Gol'dberg number(Γ)를 계산해 보았다. 각각의 값을 계산하는 수식은 Eqs. (3)과 (4)와 같다.
| $$A=\alpha_0z_0,$$ | (3) |
| $$\Gamma=(\alpha_0\overline z)^{-1},$$ | (4) |
여기서 는 열점성 감쇠 계수, 는 Rayleigh 거리, 는 평면 충격파 형성 거리를 뜻한다. 그리고 각 식에서 δ는 음 확산계수, c0는 매질 내 소리 속도, ρ0는 매질의 밀도, β는 비선형 계수 (공기 1.2)를 뜻한다.
계산 결과 1차 음파의 첫 번째 주파수 f1에서는 A = 0.046, Γ = 4.556, 두 번째 주파수 f2 에서는 A = 0.145, Γ = 7.811로 PD 모델 적용 조건인 준선형 근사에 부합하지 않는다. 즉 차주파수음의 빔 패턴 예측에 PD 모델은 적합하지 않다고 볼 수 있다. 따라서 본 논문에서는 이러한 한계점을 극복하기 위해 준선형 근사 조건이 포함되지 않는 비선형 음향 모델을 이용하여 차주파수음의 전기적 빔 조향 특성을 예측해 보았으며, 이를 실험 결과와 비교 검증하였다.
2.2 비선형 음향 모델
비선형 음향 모델의 경우, 그 식의 형태가 매우 복잡하여 특별한 경우를 제외하고는 정확한 이론적 해가 존재하지 않는다. 따라서 비선형 음향 현상을 예측하고 이해하기 위해서 수치 해석 방법이 사용 된다. 비선형 음향 현상을 예측하기 위해 사용되고 있는 수치 모델의 종류와 그 특징은 다음 표와 같다 .
Table 2에 정리 되어 있는 여러 모델 중, 파라메트릭 어레이 현상을 예측하기에 가장 적절하며, 널리 사용되고 있는 것은 KZK 방정식이다.[19] KZK 방정식은 포물형 근사로 유도된 식으로 비선형, 회절, 감쇠 효과를 고려하여 3차원 공간에서 진행하는 고지향성 음파에 대해 특징을 예측할 수 있다. 기본적인 KZK 방정식의 식 형태는 다음과 같다.
| $$\frac{\partial^2p}{\partial z\partial t'}=\frac{c_0}2\nabla_\perp^2p+\frac\delta{2c_0^3}\frac{\partial^3p}{\partial t'^3}+\frac\beta{2\rho_0c_0^3}\frac{\partial^2p^2}{\partial t'^2},$$ | (5) |
여기서 p는 음압, z는 음원으로부터 떨어진 거리, 그리고 t΄은 공간상에서 진행하는 음파를 따라가며 파형 변화를 관찰하는 시간 영역인 지연 시간을 의미하며, t – z/c0로 정의 된다.[15], [16], [21]
Table 2. Comparison of the nonlinear acoustic model.[21]
2.3 KZK 방정식의 기존 수치 해석 방법
KZK 방정식을 이용하여 파라메트릭 어레이 고지향성 음파의 특성을 예측하기 위해서 수치 해석 방법이 사용된다. KZK 방정식을 수치적으로 풀어내는 방법 중 가장 많이 사용되는 것은 ‘Texas Code’라고 불리는 Lee와 Hamilton[15], [16]에 의해 발표 및 배포된 알고리즘이다. 이 알고리즘을 이용하면 Eq. (6)와 같이 축 대칭 음원 조건을 바탕으로 비선형 고지향성 음파의 특성을 시간 영역에서 예측할 수 있다
Eq. (6)에서 알 수 있듯이 (r, z, t΄)라는 두 개의 공간과 하나의 시간 영역을 이용하므로, 짧은 시간에 특성 예측이 가능하다. 또한 KZK 방정식을 Eq. (7)와 같이 카테시안 좌표계에서 정의하여 축 대칭이 아닌 형상도 고려할 수 있는 알고리즘이 Yang과 Cleveland[17]에 의해 제안되었다.
공개된 두 수치 해석 알고리즘은 모두 유한차분법 기반으로 구성되어 있으며, 수치 해석이 진행되는 과정은 Fig. 2와 같다.
Fig. 2를 확인해보면 가장 먼저 초기 음압 경계 조건이 입력되면 이를 바탕으로 한 단계씩 음파의 진행 방향으로 나아가면서 3가지 효과(비선형, 회절, 감쇠)를 계산하게 된다. 두 가지 수치 해석 알고리즘의 초기 음압 경계 조건 설정 방식을 정리하면 Table 3과 같다. Table 3을 확인해 보면, 기존에 배포된 수치 해석 알고리즘의 경우 초기 음압 경계 조건에 하나의 동일한 음압 파형만 정의할 수 있다. 즉, 기존 수치 해석 알고리즘에 전기적 빔 조향 조건을 적용하기 위해서는 초기 조건 설정 알고리즘의 개선이 필요하다. 이에 대한 자세한 내용은 다음 장에서 설명하였다.
Table 3. Compare of the initial source boundary condition.
| Algorithm | Lee and Hamilton | Cleveland |
| Space coordinate | Axisymmetric | Cartesian |
| Pressure boundary shape | Single circular | Single circular and square |
| Pressure signal condition | Uniform pressure waveform | |
III. 전기적 빔 조향 특성 예측을 위한 수치 해석 알고리즘 구현
본 장에서는 KZK 방정식을 이용하여 차주파수음의 빔 조향 특성을 예측하기 위해 기존의 수치 해석 알고리즘을 어떻게 개선하였는지에 대해 설명하였다.
3.1 수치 해석 알고리즘 개선 방법
2.3절에서 언급하였듯이 KZK 방정식을 수치적으로 풀기 위해 축 대칭 음압 조건은 Lee의 알고리즘이, 축 대칭이 성립하지 않는 다양한 음압 조건에서는 Cleveland의 알고리즘이 사용될 수 있다. 그러나 Table 3에 정리된 바와 같이 두 알고리즘 모두 기본적으로 Fig. 3(a)와 같이 하나의 동일한 음압 파형에 대해서만 정의 되어 Fig. 1과 같은 전기적 빔 조향 경계 조건은 적용이 불가능 하였다. 따라서 기존 알고리즘을 Fig. 3(b)와 같이 배열 음원에서 발생되는 초기 음압 경계 조건도 구성할 수 있게 수정하였다.
각각 음원에 적용되는 초기 음압 경계 조건을 식으로 표현하면 Fig. 3(a)는 Eq. (8)으로, Fig. 3(b)는 Eq. (9)과 같다.
| $$\begin{array}{l}p=p_0f(t)g(x,\;y)\;at\;z=0\\g(x,y)=\left\{\begin{array}{l}1,\;x_1\leq x\leq x_n\;and\;y_1\leq y\leq y_n\\0,\;otherwise\end{array}\right..\end{array}$$ | (8) |
여기서 f(t)는 초기 음압 발생 파형, g(t)는 공간상에 정의된 진폭 쉐이딩 함수, 그리고 m 은 배열을 구성하는 음원의 채널 번호(1 to N)를 의미한다. Eq. (8)은 기존 알고리즘에 적용된 방법으로 하나의 동일한 음압 파형만 고려할 수 있다. 이와 비교하여 Eq. (9)의 fm(t)를 보면 배열을 구성하는 각각의 경계 조건에 서로 다른 초기 음압 경계 조건을 적용할 수 있다. 따라서 Fig. 3(b), Eq. (9)의 개선 알고리즘을 적용하면, 기존의 수치 해석 프로그램에서는 예측이 불가능 하였던 음원 배열에서 발생하는 비선형 음향 방사 특성 예측이 가능하다. 즉, Fig. 1의 전기적 빔 조향 특성을 예측할 수 있다.
3.2 전기적 빔 조향 특성 예측을 위한 초기 음압 경계 조건
전기적 빔 조향 시스템을 이용하여 차주파수음 발생 방향을 조절하기 위해서는 Fig. 1과 같이 배열을 구성하고 있는 음원에 가해지는 구동 신호, fm(t)를 각각의 채널별로 조절하는 것이 필수적이다.[13], [14], [19] 이를 수치 해석에 동일하게 적용하기 위해서 fm(t)는 다음 식과 같이 정의된다.
| $$\begin{array}{l}f_m(t)=p_1\sin\lbrack2\pi f_1(t-m\triangle t)\rbrack\\\;\;\;\;\;\;\;\;\;\;\;\;+p_2\sin\lbrack2\pi f_2(t-m\triangle t)\rbrack,\end{array}$$ | (10) |
여기서 f1, f2는 파라메트릭 어레이 음원에서 발생되는 1차 음파의 주파수, p1, p2는 각각 1차 음파 주파수가 구동되는 음압의 크기를 뜻한다. 그리고 Δt는 Eq. (11)와 같이 정의되며, 원하는 빔 조향 각도 θ 에 해당하는 시간 지연을 의미한다.
| $$\triangle t=\frac d{c_0}\sin\theta,$$ | (11) |
여기서 d는 Fig. 1의 배열을 구성하는 음원 채널 사이의 간격을 의미한다. 따라서 전기적 빔 조향 특성 예측을 위한 초기 음압 조건을 Eqs. (10)과 (11)을 바탕으로 결정하였다.
IV. 수치 해석 결과 및 고찰
개선된 알고리즘을 통해 계산된 차주파수음의 빔 조향 특성의 정확성을 검증하기 위해서 실제 실험 결과와 비교해 보았다. 이를 위해 수치 해석을 위한 초기 음압 조건도 Table 1에서 정리한 실험 조건과 동일하게 설정하였다. 다만 빔 조향 특성을 실험에서는 10°에서 40°까지 10° 간격으로 확인해 보았으나, 포물형 근사로 정의된 KZK 방정식은 음향 방사 방향에서 20° 내외의 범위에서만 높은 정확도로 음향 특성 예측이 가능하다고 알려져 있으므로[15], [21] 음향 방사 방향에서 최대 –30° ~ +30° 범위로만 공간 영역 그리드를 설정하고 해석을 진행하였다. 그리고 실험과 동일하게 음원으로부터 0.8 m 떨어진 거리에서 빔 조향 특성을 계산하였으며, 이를 실험 결과와 비교해 보았다.
4.1 초기 음압 경계 조건 입력 결과
빔 조향 각도 θ 조건을 Eqs. (10)과 (11)에 적용하면 빔 조향 각도에 따른 시간 지연 값과 무차원 지연 시간 (τ = ω0t΄) 값이 계산되며, 이를 정리하면 Table 4와 같다. 여기서 무차원 지연 시간은 KZK 방정식 수치 해석에서 사용되는 시간 영역으로 2.2장에서 언급한 지연 시간에 ω0 = 2πf 를 곱한 값으로, f = 100.8 kHz를 사용했다.
Table 4. Time delay and dimensionless retarded time delay corresponding to steering angle.
| Steering angle | Time delay | Dimensionless retarded time delay | |
| Ch1 - Ch2 | Ch1 - Ch16 | ||
| 10° | 1.52e-6 s | 0.962 | 14.429 |
| 20° | 2.99e-6 s | 1.895 | 28.419 |
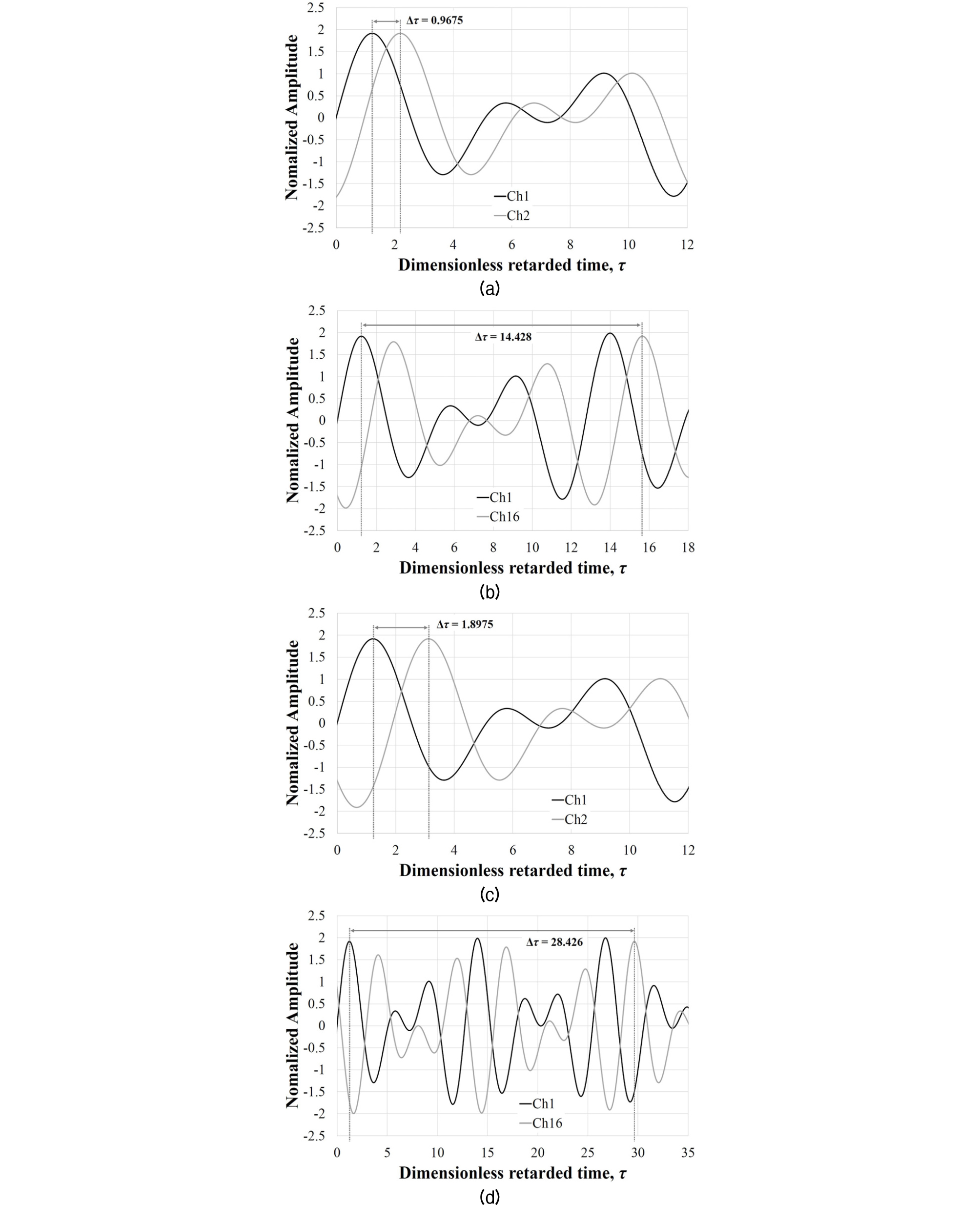
전기적 빔 조향 시스템 구현을 위해 Table 4의 결과 값을 Eqs. (9)와 (10)을 이용하여 16개 채널에 입력하였다. 이때 16개 채널로 구성된 배열을 Fig. 3(b)와 같은 형태로 수치 해석 알고리즘에 적용하기 위해서는 초기 음압 경계 조건 구현을 위한 공간 영역 그리드 간격을 적절히 설정해 주어야 한다. 본 논문에서는 Table 1에 정리된 채널 사이의 간격을 정확하게 표현하기 위해 그리드 간격을 0.5 mm로 설정하였다.
Fig. 4(a) ~ (d)을 확인해 보면 빔 조향 각도에 따라 채널 별 초기 음압 경계 조건, 무차원 지연 시간이 Table 4에 정리된 것과 매우 유사하게 잘 적용되어 있는 것을 볼 수 있다. Fig. 4의 결과와 Table 4가 정확하게 일치 하는 것이 아닌, 매우 유사하게 나타나는 이유는 KZK 방정식을 수치 해석 하기 위해 사용된 시간 영역 해상도의 한계 때문이다. 만일 시간 영역 해상도가 무한대로 크다면 Fig. 4의 결과와 Table 4가 정확하게 일치할 수 있을 것이다. 하지만 그렇게 된다면 계산 량이 무한대로 증가하여 실제 계산 결과를 얻기 힘들다. 따라서 본 연구에서는 시간 영역 해상도를 Table 4에서 정리된 무차원 지연 시간값과 수치 해석에서 구현된 값을 비교하여 상대오차 0.5 %내외의 수준이 되도록 설정하였다. 이를 통해 수치 해석에서 사용된 무차원 지연 시간 간격은 0.0251이다. 그리고 수치 해석 결과와 연속된 사인파 신호 입력으로 측정된 실험 결과를 비교하기 위해서 전체 시간 범위는 Eq. (10)이 20파장 포함 되도록 설정하였다.
4.2 차주파수음 빔 조향 특성 수치 해석 결과
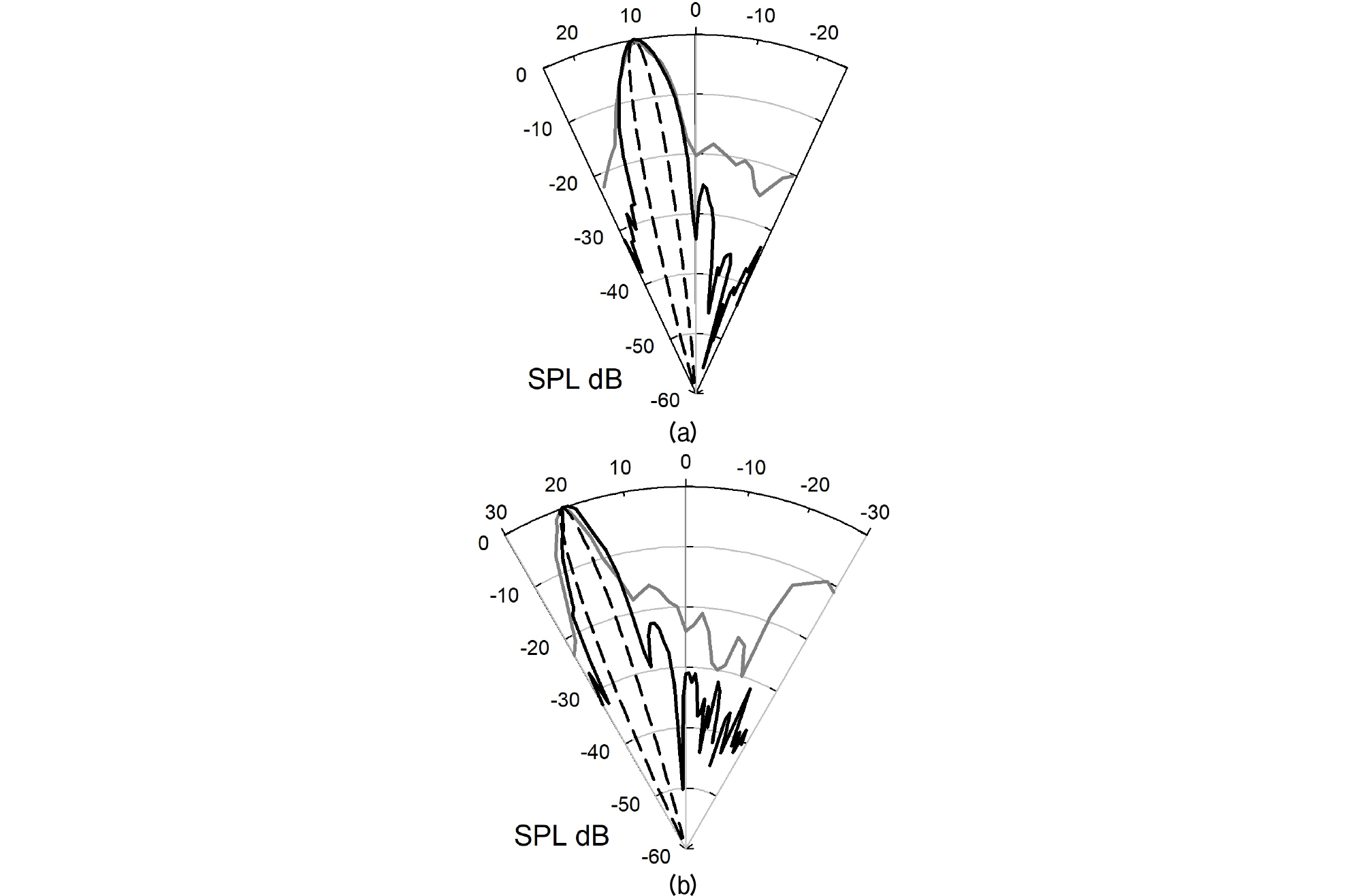
4.1절에서 언급한 초기 음압 경계 조건을 이용, 조향 각도 θ 만큼 시간 지연을 적용하여 KZK 방정식 수치 해석을 진행하였다. 그리고 음원으로부터 0.8 m 떨어진 거리에서 차주파수음 빔 패턴을 계산 하였으며, 이를 실험 결과[19] 및 PD 모델 결과와 비교 하였다. Fig. 5는 수치 해석 결과와 실험 결과를 비교한 그래프이다. Fig. 5(a)는 빔 조향 각도가 10°의 경우이며, Fig. 5(b)는 빔 조향 각도가 20°의 경우이다. 각 그래프에서 회색 선은 실험 결과, 검정색 선은 KZK 방정식 수치 해석 결과, 그리고 검정색 점선은 Eqs. (1)과 (2)를 이용하여 계산된 PD 모델 결과이다.[10] 이때 PD 모델 결과는 Table 1과 동일한 방사 영역을 가진 가우시안 음원 가정으로 도출되었다.
Fig. 5를 확인해 보면, 기본적으로 KZK 방정식 수치 해석 결과 주엽이 원하는 빔 조향 각도에 맞게 적절히 움직인 모습을 볼 수 있다. 이를 실험 결과와 비교해 보면, 빔 조향 각도가 10°인 Fig. 5(a)의 경우 실험 결과, KZK 방정식 해석 결과에서 주엽의 반치 빔폭이 5°로 이 매우 잘 일치하는 모습을 볼 수 있다. 빔 조향 각도가 20°인 Fig. 5(b)의 경우 주엽이 0.25° 어긋나는 형태를 볼 수 있는데, 이는 실험 결과가 20.25°만큼 조향되었기 때문이다. 그렇지만 주엽의 반치 빔폭이 5°로 잘 일치함을 볼 수 있다. 그러나 PD 모델 계산 결과 주엽의 반치 빔폭은 2.4°로 실험 결과 및 KZK 방정식 수치 해석 결과에 비해 48 % 수준으로 좁게 나타났다. 이와 같이 오차가 발생한 이유는 먼저 서론에서 언급하였듯이 PD 모델은 주엽의 반치 빔폭이 실험 결과에 비해 좁게 나타나기 때문이다. 또한 본 논문에서 사용한 파라메트릭 어레이 초음파 거리센서는 준선형 근사 조건과 가우시안 음원에 해당되지 않기 때문이다.
Fig. 5(a), (b)에서 KZK 방정식 해석 결과와 실험 결과의 주엽이 잘 일치하는 것과 달리 1차 음파의 부엽으로 인해 발생된 차주파수음 부엽[9], [19], [22]의 경우 차이가 발생하는 것을 볼 수 있다. 이는 수치 해석에서는 전기적 빔 조향 시스템을 구현하는 초기 음압 경계 조건이 음원에서 발생되는 이상적인 값으로 입력되었지만, 실험에서 사용된 초음파 음원인 pMUT은 MEMS 제작 방식의 한계로 인해 전기적 빔 조향 시스템을 구성하는 모든 음원이 동일하게 구동되지 못하였기 때문이다. 또한 실제 음원은 배열 구성을 위한 주변 구조물이 존재하며,[19] 이로 인해 표면 음압 조건이 수치 해석에 사용된 이상적인 초기 음압 경계 조건과 다소 차이가 발생하기 때문이다. 그렇지만 KZK 방정식 해석 결과에서 부엽의 발생 위치는 적절히 예측할 수 있음을 볼 수 있다. 예를 들어 빔 조향 각도 θ = 10°에서는 –2°, -15°, -25° 부근, 빔 조향 각도 θ = 20°에서는 10°, 5°, -15°, -20° 부근이 이에 해당한다.
V. 결 론
본 논문에서는 준선형 근사 조건에 해당되지 않는 파라메트릭 어레이 음원에서 발생하는 고지향성 차주파수음 조향 특성을 예측해 보았다. 이를 위해 파마레트릭 어레이 현상 예측에 널리 사용되는 KZK 방정식을 이용하였으며, 전기적 빔 조향 시스템 구현을 위해 기존 KZK 방정식 수치 해석 방법이 가지고 있던 알고리즘의 한계점을 개선하였다. 먼저 단일 채널의 음원만 고려가 가능했던 부분을 배열 음원도 고려가 가능하도록 수정 하였으며, 두 번째로 각 채널 별로 다양한 초기 음압 경계 조건이 입력 가능하도록 개선하였다. 개선된 수치 해석 알고리즘을 바탕으로 강한 차주파수음을 발생시키는 초음파 거리센서의 빔 조향 특성을 계산하고, 실험 결과와 비교해 보았다. 그 결과 주엽의 조향 각도, 빔 폭이 해석 결과와 실험 결과가 잘 일치함을 볼 수 있었다. 부엽의 경우 해석 결과와 실험 결과에 다소 많은 차이가 보였으나, 이는 실험 조건과 이상적인 해석 조건 사이의 차이로 인해 발생한 오차로 판단된다. 그럼에도 부엽이 발생되는 위치를 적절히 예측할 수 있음이 확인되었다. 종합해보면, 본 연구에서 사용한 KZK 방정식 수치 해석 알고리즘 개선 방법을 이용하면 준선형 근사 조건에 해당되지 않는, 다양한 파라메트릭 어레이 음원에 대해서 차주파수음의 빔 조향 특성이 예측 가능할 것으로 판단된다.