Submarine bistatic target strength analysis based on bistatic-to-monostatic conversion

Kookhyun Kim; Sung-Ju Park; Keunhwa Lee; Dae-Seung Cho

doi:10.7776/ASK.2024.43.1.138

Preview

Research Article

The Journal of the Acoustical Society of Korea. 31 January 2024. 138-144
https://doi.org/10.7776/ASK.2024.43.1.138

Submarine bistatic target strength analysis based on bistatic-to-monostatic conversion

양상태-단상태 변환 기반 잠수함 양상태 표적강도 해석

Kookhyun Kim¹

Sung-Ju Park¹

Keunhwa Lee²

Dae-Seung Cho³^*

김 국현¹

박 성주¹

이 근화²

조 대승³^*

¹동명대학교 해양모빌리티학과

²세종대학교 국방시스템공학과

³부산대학교 조선해양공학과

^{*Corresponding Author}

ABSTRACT

This paper presents a bistatic to monostatic conversion technique to analyze the bistatic target strength of submarines. The technique involves determining the transmission path length of acoustic waves, which are emitted from a source, scattered off an underwater target, and eventually received by a receiver. By generating a corresponding virtual scattering surface, this method effectively transforms the target strength analysis problem from bistatic to monostatic. The converted monostatic target strength problem can be assessed using a well-established monostatic numerical methods. The bistatic target strength analysis for Benchmark Target Strength Simulation (BeTTSi), a widely used target strength model were performed. The results were compared with those calculated by boundary element methods and Kirchhoff approximation, and confirmed the validity and the practical applicability of the proposed analysis technique for evaluating submarine target strength.

Keywords

Bistatic target strength

Bistatic to monostatic conversion

Equivalent transmission-path length

Equi-phase virtual scattering surface

본 논문에서는 잠수함 양상태 표적강도 해석을 위한 양상태-단상태 변환 기법을 제안하였다. 이 기법은 송신 음원이 수중 표적면에 의해 산란된 후 수신자에 도달하는 음파 전달 경로 길이를 산정하고, 이에 상응하는 가상 산란면을 생성함으로써, 수중 표적의 표적강도 문제를 양상태에서 단상태로 변환하는 방법이다. 변환된 단상태 표적강도 문제는 기 정립된 단상태 표적강도 수치 해석 기법을 활용하여 양상태 표적강도를 평가한다. 표적강도 표준 모델로 활용되고 있는 BeTTSi에 대한 양상태 표적강도 해석을 수행하였으며, 그 결과는 경계 요소법과 키르히호프 근사에 의한 해석 결과와 비교하여 제안된 해석 기법의 신뢰성과 잠수함 표적강도 평가 도구로서의 실무 활용성을 확인하였다.

키워드

양상태 표적강도

양상태-단상태 변환

등가 전달경로 길이

등위상 가상 산란면

MAIN

I. 서 론
II. 양상태 표적강도 해석
2.1 소나단면적과 표적강도
2.2 키르히호프-헬름홀츠 적분방정식
2.3 키르히호프 근사
2.4 양상태-단상태 변환 기반 표적강도 해석
III. 수치해석
3.1 수치해석 모델 및 해석조건
3.2 수치해석 결과
IV. 결 론

I. 서 론

표적강도는 잠수함의 능동소나 대응측면에서 중요한 성능지표이며, 이를 정량적으로 평가하기 위한 다양한 수치해석기법이 개발․적용되어 왔다.^[1,2]잠수함과 같은 대형 복합구조물의 표적강도는 주로 고주파수 해석이론에 기반해 평가되어 왔다. 특히, 송신소나와 수신소나가 동일한 위치에 있다고 가정하는 단상태에 대한 수치해석기법들이 잘 정립되어 실무에 활용되고 있다. Kim et al.^[3]은 물리광학법 즉, 키르히호프 근사에 기반한 고주파수 해석기법을 이용해 잠수함의 주파수 영역에서의 단상태 표적강도를 평가하였다. Kim et al.^[4]은 키르히호프 근사와 역푸리에변환 기법을 이용한 고주파수 시간영역에서의 단상태 표적강도 해석기법을 구현하고 잠수함모델에 대한 시간영역 후방산란파를 해석하였다. Choi et al.^[5]또한 키르히호프 근사에 기반한 단상태 표적강도 수치해석기법을 제안하고 정확도 검증을 위한 잠수함 모형 수조시험을 실시하였다. Gilroy et al.^[6]과 Nihof et al.^[7]은 수중표적의 표적강도 평가기법의 정확도 검증을 위한 표준 모델인 Benchmark Target Strength Simulation (BeTSSi)에 대해 세계 유수 기관이 개발․보유하고 있는 소프트웨어를 이용해 단상태 고주파수 표적강도 해석을 수행하고 그 결과를 상호 비교하였다.

소나 운용의 효율성 측면에서 양상태 표적강도의 중요성이 점차 증대되고 있다.^[8,9,10] 이에 양상태 표적강도의 정량 평가를 위한 수치해석기법들이 제안되었다. Choo et al.^[11]은 양상태 소나의 표적식별 정확도 비교를 위해 구와 원통에 대한 수치해석과 수조실험을 수행하고 그 결과를 수치해석결과와 비교하였다. Ji et al.^[12]은 잠수함 모형의 양상태 표적강도 수조시험을 수행하고 그 결과를 키르히호프 근사에 기반한 수치해석결과와 비교하였다.

한편, 수중표적에 대한 음향 산란 현상은 후방산란과 전방산란으로 구분해 설명할 수 있다. 단상태의 경우, 후방산란이 지배적으로 나타나는 반면, 양상태의 경우, 후방산란뿐 아니라 전방산란의 영향이 매우 크게 나타난다. 따라서 양상태 표적강도를 정도 높게 해석하기 위해서는 후방산란과 전방산란을 함께 해석할 수 있는 수치해석기법이 필요하다.

기존의 키르히호프 근사에 기반한 고주파수 표적강도 수치해석기법은 후방산란의 영향이 지배적인 단상태 표적강도 해석에는 매우 유용한 반면, 전방산란의 영향이 크게 나타나는 산란방향에 대한 양상태 표적강도 해석에는 적합하지 않다. 이에 Liu et al.^[13]은 입사 음영구역에 대한 음향학적 경계조건을 적용해 전방산란의 영향을 고려할 수 있는 수정된 키프히호프 근사식을 유도하고 구, 원통, 잠수함모델 등에 대한 수치해석을 통해 그 타당성을 확인하였다.

본 논문에서는 후방산란과 전방산란을 동시에 고려할 수 있는 양상태 표적강도 해석을 위한 새로운 고주파수 수치해석기법을 정립한다. 이는 송신소나로부터 출발해 수중표적에 산란되어 수신소나에 도달하는 음파의 전체 경로길이를 산정하고 이에 등가되는 가상 산란면을 생성함으로써 수중표적의 표적강도 문제를 양상태에서 단상태로 변환하는 방법이다. 변환된 단상태 표적강도 문제는 기 정립되어 있는 단상태 표적강도 수치해석기법을 적용할 수 있다. 제안된 해석기법의 신뢰성과 실무 활용성을 검증하기 위해 표준 잠수함 모델(BeTSSi)^[6,7]에 대한 양상태 표적강도 해석을 수행하고 그 결과를 상용 S/W의 경계요소법과 키르히호프 근사에 의한 해석결과와 비교한다.

II. 양상태 표적강도 해석

2.1 소나단면적과 표적강도

수중표적에 대한 음향산란 특성은 Eq. (1)의 소나단면적으로 정의되며, 표적강도는 Eq. (2)와 같이 소나단면적으로부터 환산할 수 있다.^[3]

(1)

σ = \lim_{R \to \infty} (4 π R^{2} \frac{| p_{s} |^{2}}{| p_{i} |^{2}}),

(2)

T S = 10 \log_{10} (\frac{σ}{4 π}),

여기서 𝜎는 소나단면적( $m^{2}$ )이며, $T S$ 는 표적강도(dB)이다. $R$ 은 표적 기준점으로부터 소나까지의 거리(m), $p_{i}$ 와 $p_{s}$ 는 음원와 수신자 각각 위치에서의 입사음압과 산란음압(Pa)이다.

2.2 키르히호프-헬름홀츠 적분방정식

Fig. 1과 같이 3차원 공간에서 입사파에 의해 형성되는 산란음장은 Eq. (3)의 키르히호프-헬름홀츠 적분방정식으로부터 산정할 수 있다.

https://static.apub.kr/journalsite/sites/ask/2024-043-01/N0660430116/images/ASK_43_01_16_F1.jpg

Fig. 1.

(Color available online) Cartesian coordinates for acoustic wave scattering problem of underwater target.

(3)

p_{s} ({\vec{r}}_{r}) = \int_{S} [p (\vec{r}) \frac{\partial G (\vec{r}, {\vec{r}}_{r})}{\partial n} - G (\vec{r}, {\vec{r}}_{r}) \frac{\partial p (\vec{r})}{\partial n}] d S,

여기서 $p_{s} ({\vec{r}}_{r})$ 은 수신자 위치벡터 ${\vec{r}}_{r}$ 에서의 산란음압(Pa)을 나타내며, $p (\vec{r})$ 은 표적면 임의 위치벡터 $\vec{r}$ 에서 입사음장과 표적면의 산란특성에 의해 유기되는 음압(Pa)이다. $G (\vec{r}, {\vec{r}}_{r})$ 는 Eq. (4)와 같이 정의되는 그린함수이며, $\partial (\cdot) / \partial n$ 은 단위법선방향 편미분을 의미한다.

(4)

G (\vec{r}, {\vec{r}}_{r}) = \frac{e^{j k r_{r}}}{4 π r_{r}},

여기서 $j$ 는 단위허수( $= \sqrt{(- 1)}$ )이며, $k$ 는 파수( $= 2 π f / c$ ), $f$ 와 $c$ 는 주파수(Hz)와 음속(m/s)를 나타낸다. 또한, $r_{r}$ 은 표적면과 수신자 간의 거리(= $| {\vec{r}}_{r} - \vec{r} |$ , m)이다.

2.3 키르히호프 근사

음향산란문제에서 키르히호프 근사를 적용하면 Eq. (3)에서 표적면에 유기되는 음장 $p (\vec{r})$ 은 Eq. (5)와 같이 입사음장 $p_{i} (\vec{r})$ 과 산란음장 $p_{s} (\vec{r})$ 의 합으로 가정할 수 있다.

(5)

p (\vec{r}) = p_{i} (\vec{r}) + p_{s} (\vec{r}) .

한편, 음원이 점 음원일 경우, 표적면임의 위치벡터 $\vec{r}$ 에서의 입사음압 $p_{i} (\vec{r})$ 은 Eq. (6)과 같다.

(6)

p_{i} (\vec{r}) = \frac{P_{0}}{r_{s}} e^{j k r_{s}},

여기서 $P_{0}$ 는 음원의 진폭이며, $r_{s}$ 은 표적면 임의 위치 $\vec{r}$ 와 음원 간의 거리(= $| {\vec{r}}_{s} - \vec{r} |$ , m)이다.

Fig. 2는 양상태에서의 음원과 수신자의 방향에 따른 기하학적인 가시면과 비가시면을 도시한 것이다. $S_{1}$ 은 음원에 대해서는 가시면이지만, 수신자에 대해서는 비가시면이 된다. $S_{2}$ 는 음원과 수신자 모두에 대해 가시면이 되며, $S_{3}$ 는 음원에 대해서는 비가시면, 수신자에 대해서는 가시면, $S_{4}$ 는 음원과 수신자 모두에 대해 비가시면이 된다.

https://static.apub.kr/journalsite/sites/ask/2024-043-01/N0660430116/images/ASK_43_01_16_F2.jpg

Fig. 2.

(Color available online) Visible and invisible surfaces from source and receiver.

기존 키르히호프 근사에서는 $S_{2}$ 에 유기되는 후방산란 음장만을 고려하였으며, 이로 인해 $S_{3}$ 에 의한 전방산란 음장은 무시되었다.^[12] 본 연구에서는 양상태 표적강도 해석에서 전방산란음장을 고려하기 위해 Eq. (7)과 같이 수신자에 대한 가시면인 $S_{2}$ 과 $S_{3}$ 에 대해 강체경계조건과 음영경계조건을 각각 적용하였다.

(7)

\{\begin{cases} \frac{\partial (p_{s} + p_{i})}{\partial n} = 0, o n S_{2} \\ p_{s} + p_{i} = 0 o n S_{3} \end{cases} .

Eqs. (4), (5), (6)을 Eq. (3)에 대입하고 Eq. (7)의 경계조건을 적용하여 정리하면 Eq. (8)과 같은 후방산란음장 성분[Eq. (9)]과 전방산란음장 성분[Eq. (10)]의 합으로 구성된 양상태 음향산란 산정식을 얻을 수 있다. 이는 Liu et al.^[13]이 유도한 식과 동일한 결과이며, 이를 이용해 수중표적에 대한 고주파수 양상태 표적강도 해석이 가능하다.

(8)

p_{s} = - \frac{i k P_{0}}{4 π} (I_{2} + I_{3}),

(9)

I_{2} = \int_{S_{2}} \frac{e^{i k (r_{s} + r_{r})}}{r_{s} r_{r}} \{\hat{n} \cdot ({\hat{r}}_{s} + {\hat{r}}_{r})\} d S,

(10)

I_{3} = \int_{S_{3}} \frac{e^{i k (r_{s} + r_{r})}}{r_{s} r_{r}} \{\hat{n} \cdot ({\hat{r}}_{s} - {\hat{r}}_{r})\} d S,

여기서 ${\hat{r}}_{s}$ 와 ${\hat{r}}_{r}$ 은 Fig. 1에 도시한 바와 같이 표적 기준점으로부터 음원과 수신자까지의 단위방향벡터를 각각 의미한다. 또한, $\hat{n}$ 은 표적면 상의 단위법선벡터이다.

2.4 양상태-단상태 변환 기반 표적강도 해석

본 연구에서는 Eq. (8)의 양상태 산란음장을 효율적으로 산정하기 위해 양상태-단상태 변환을 기반으로 한 새로운 표적강도 해석기법을 제안하였다. 이는 양상태 문제에 대한 기하학적 변환을 통해 상대적으로 알고리즘 구현이 간단한 단상태 문제로 해석할 수 있다는 장점이 있다.

제안된 해석기법은 Fig. 3에 보인 바와 같이 ①양상태 표적강도 수치해석모델을 ②가상산란면 기반의 등위상변환을 통해 ③단상태 수치해석모델로 변환하고, ④이에 대한 단상태 고주파수 해석을 수행하여, 최종적으로 ⑤대상표적에 대한 양상태 고주파수 표적강도를 산정하는 절차를 따른다.

https://static.apub.kr/journalsite/sites/ask/2024-043-01/N0660430116/images/ASK_43_01_16_F3.jpg

Fig. 3.

(Color available online) Bistatic target strength analysis procedure based on bistatic to monostatic conversion using equivalent-path length based virtual scattering surface.

본 연구에서 제안한 양상태-단상태 변환기법을 수치해석적으로 구현하기 위해 단상태 표적강도 해석에서 다중반사 효과를 고려하기 위해 적용되는 가상면개념^[3,14]을 도입하면, Fig. 4에 도시한 바와 같이 평면파가 표적면에 입사할 때, 음원으로부터 출발한 평면파가 표적면에 산란되어 수신자로 돌아가는 전체 전달경로를 산정하고 이에 등가되는 위치 즉, 전체 전달경로의 1/2에 해당하는 위치에 등 위상 가상 산란면을 형성할 수 있다.

https://static.apub.kr/journalsite/sites/ask/2024-043-01/N0660430116/images/ASK_43_01_16_F4.jpg

Fig. 4.

(Color available online) Virtual scattering surface concept.

일반적으로 표적강도 수치해석 모델은 유한개의 정점들과 이를 연결하는 요소들로 구성된다. 본 연구에서는 잠수함을 삼각형 평면요소로 모델링하고 원 정점에 대한 가상 정점을 산정(Fig. 5)하여 가상 산란면으로 구성된 단상태 수치해석모델을 생성한다. 이때, 원 정점으로부터 가상 정점으로의 이동벡터 $\vec{Δ}$ 는 Eq. (11)으로부터 산정한다.

https://static.apub.kr/journalsite/sites/ask/2024-043-01/N0660430116/images/ASK_43_01_16_F5.jpg

Fig. 5.

(Color available online) Moving vector calculation of scatter on target surface.

(11)

\vec{Δ} = - (\vec{r} \cdot - \frac{(\hat{r_{s}} - \hat{r_{r}})}{2}) \hat{r_{r}} .

양상태에서 단상태로 변환된 수치해석모델을 이용해 Eq. (12)에 의거 양상태 표적강도 해석을 수행한다.

(12)

T S = 10 \log_{10} [\frac{k^{2}}{4 π^{2}} {|\int_{S_{v}} e^{2 i k r_{r}} ({\hat{n}}_{v} \cdot {\hat{r}}_{r}) d S|}^{2}] .

III. 수치해석

3.1 수치해석 모델 및 해석조건

본 연구에서 제안한 수치해석기법의 신뢰성과 실무적용성을 검증하기 위해 60 m급 가상 잠수함에 대한 수치해석을 수행하고 그 결과를 상용 S/W인 COMSOL Physics^[15] 해석결과와 비교하였다.

수치해석모델은 표적강도 표준 모델인 BeTSSi^[6,7]로써, 그 크기는 62 m × 7 m × 11 m이다. 대상모델은 함수방향, 좌현방향, 높이방향을 각각 x-y-z 직교좌표계의 양의 방향으로 정의하고 원점에 주선체 중앙부가 위치하도록 하였다. 대상 모델의 외부 면은 총 59,618개의 평면삼각형 요소로 모델링하였으며(Fig. 6), 이때, 평면삼각형 요소의 한변의 길이는 해석주파수 상한에 대응하는 파장의 약 1/10의 범위에 있도록 하였다.

https://static.apub.kr/journalsite/sites/ask/2024-043-01/N0660430116/images/ASK_43_01_16_F6.jpg

Fig. 6.

(Color available online) Numerical analysis model : BeTSSi.

수치해석 조건은 Table 1에 정리한 바와 같다. 매질의 음속은 1,500 m/s이며, 음원 주파수는 100 Hz, 500 Hz, 1 kHz, 1.5 kHz, 2 kHz 등 총 5개로 설정하였다. 해당 주파수는 파장으로 환산하면, 각각 15 m, 3 m, 1.5 m, 1 m, 0.75 m이며, 이는 제안된 기법의 저주파수영역부터 중주파수영역까지의 검증을 위함이다. 음원 입사벡터와 수신자 산란벡터는 $x - y$ 평면 상(고각 0°)에서 $x$ -축으로부터의 방위각으로 정의할 때, 음원 입사 방위각은 240°이며, 수신자 산란 방위각은 0° 에서 360°까지 0.2° 간격으로 설정하였다.

Table 1.

Numerical analysis condition.

Sound speed (m/s)		1,500
Frequency (Hz)		100, 500, 1,000, 1,500, 2,000
Source	Elevation angle (o)	0
Source	Azimuth angle (o)	240
Receiver	Elevation angle (o)	0
Receiver	Azimuth angle (o)	0 ~ 360, 0.2 step

3.2 수치해석 결과

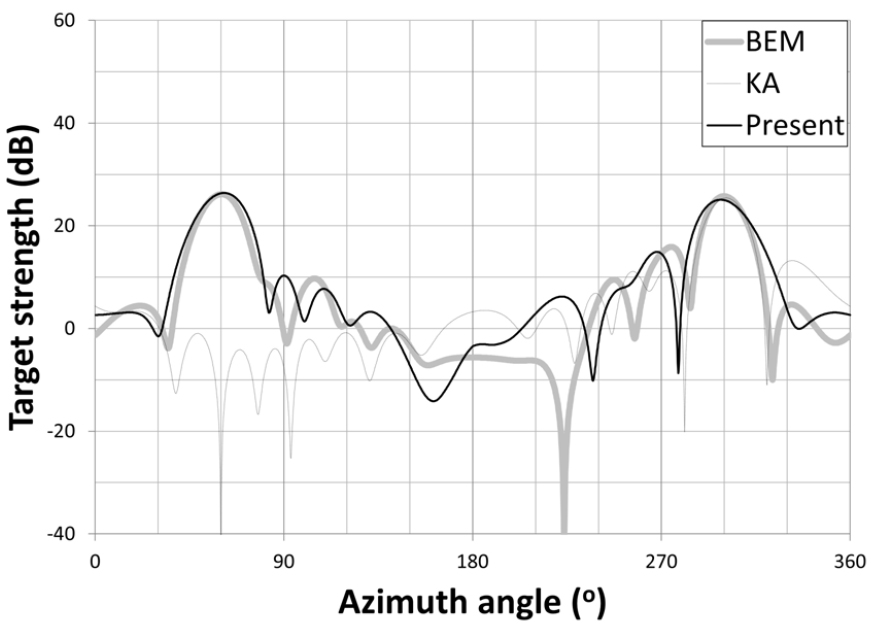
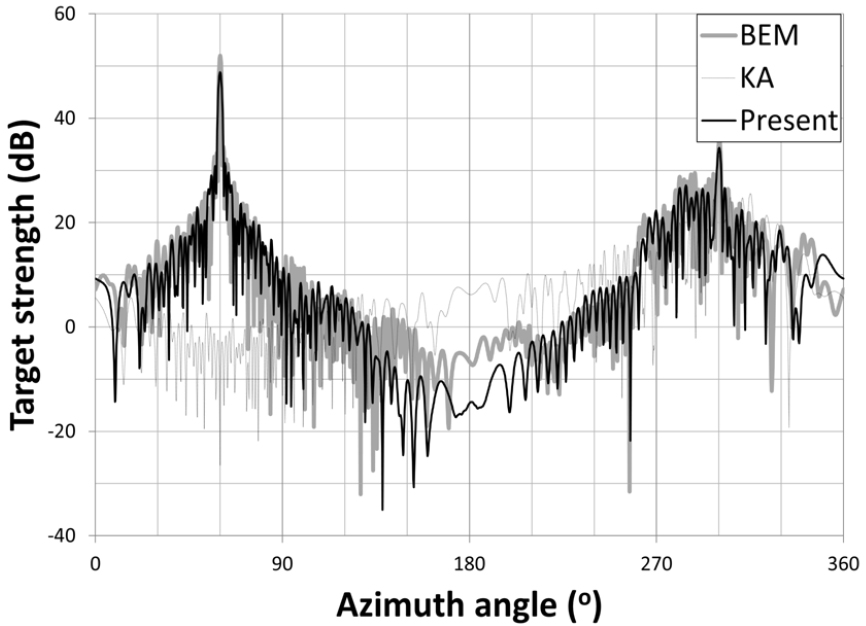
수치해석모델에 대한 양상태 표적강도 해석결과는 Fig. 7에서 Fig. 11까지 주파수별로 나타내었다. 이때, 제안된 해석기법(Present)의 신뢰성과 주파수 영역에 따른 실무 적용성을 검토하기 위해 COMSOL physics의 저주파수 해석모듈인 경계요소법(Boundary Element Method, BEM)과 고주파수 해석모듈인 키르히호프 근사(Kirchhoff Approximate, KA)에 의한 수치해석결과를 비교하여 도시하였다.

https://static.apub.kr/journalsite/sites/ask/2024-043-01/N0660430116/images/ASK_43_01_16_F7.jpg

Fig. 7.

Bistatic target strength of BeTSSi (@100 Hz).

https://static.apub.kr/journalsite/sites/ask/2024-043-01/N0660430116/images/ASK_43_01_16_F8.jpg

Fig. 8.

Bistatic target strength of BeTSSi (@500 Hz).

https://static.apub.kr/journalsite/sites/ask/2024-043-01/N0660430116/images/ASK_43_01_16_F9.jpg

Fig. 9.

Bistatic target strength of BeTSSi (@1,000 Hz).

https://static.apub.kr/journalsite/sites/ask/2024-043-01/N0660430116/images/ASK_43_01_16_F10.jpg

Fig. 10.

Bistatic target strength of BeTSSi (@1,500 Hz).

https://static.apub.kr/journalsite/sites/ask/2024-043-01/N0660430116/images/ASK_43_01_16_F11.jpg

Fig. 11.

Bistatic target strength of BeTSSi (@2,000 Hz).

BEM 해석결과와 비교할 때, 주파수와 상관 없이 표면적이 넓은 잠수함 측면에 의한 거울반사에 해당하는 수신 방위각 300°와 완전 전방산란에 해당하는 수신 방위각 60°에서 부합성이 매우 높게 나타나고 있다. 반면, 그 외의 방위각에 대해서는 상대적으로 부합성이 낮게 나타나고 있으며, 이는 BEM에서 고려 가능한 다중반사효과, 모서리에 의한 회절 등의 고차 항에 의한 영향이 포함되지 않았기 때문인 것으로 사료된다. 일반적으로 이러한 고차 항에 의한 영향은 주파수가 낮을수록 크게 나타난다. 따라서 본 수치해석결과에서도 높아질수록 효과가 그 차이가 작아지며, 1,500 Hz와 2,000 Hz에서는 그 차이가 더욱 작게 나타난다.

한편, KA 해석결과와 비교할 때, 제안된 해석기법(Present)이 KA이 포함하지 못하는 전방산란 성분을 잘 모의하고 있으며, 고주파수로 갈수록 정도 높은 결과를 보임을 알 수 있다. 이상의 결과로부터, 본 연구에서 제안한 양상태 표적강도 해석기법이 성공적으로 정립되었으며, 잠수함과 같은 대형 수중표적에 대한 표적강도 평가에 실무적으로 신뢰성 있게 활용될 수 있음을 알 수 있다.

IV. 결 론

본 논문에서는 양상태-단상태 변환에 기반한 양상태 표적강도 해석기법을 새롭게 제안하였다. 제안된 양상태-단상태 변환기법은 음원과 표적면, 수신자의 등가 전달경로를 기하학적 변환으로 정식화되었다. 잠수함 표준 모델인 BeTSSi에 대한 양상태 표적강도 해석을 수행하였다. 해석결과는 상용 S/W의 저주파수 및 고주파수 해석모듈에 의한 결과와 비교하여 제안된 해석기법의 신뢰성과 실무적용성을 확인하였다.

본 연구는 단일반사가 지배적으로 나타나는 잠수함의 외부형상에 한정되어 있다. 따라서 향후 잠수함 내부구조 및 외부 부가형상에 의한 다중반사효과, 음향타일에 의한 흡음효과, 모서리에 의한 회절효과 등을 고려할 수 있는 고도화 연구가 요구된다. 또한, 본 연구결과의 실무 적용성을 높이기 위해 제안된 해석기법과 기존 해석기법 간의 연산속도 비교 및 그에 따른 연산 고속화 연구도 함께 요구된다.

Acknowledgements

이 과제는 부산대학교 기본연구지원사업(2년)에 의하여 연구되었음.

References

R. J. Urick, Principles of Underwater Sound (Peninsular Publishing, Los Altos Hills, 1983), pp. 331-341.

G. D. Tyler, "The emergency of low-frequency active acoustics for as a critical antisubmarine warfare technology," John Hopkins APL Technical Digest, 13, 145-159 (1992).

K.-H. Kim, D.-S. Cho, and J.-C. Kim, "High frequency acoustic scattering analysis of underwater target" (in Korean), J. Soc. Nav. Archit. Korea, 42, 528-533 (2005).

10.3744/SNAK.2005.42.5.528

K. Kim, D. Cho, and W. Seong, "Simulation of time-domain acoustic wave signals backscattered from underwater targets" (in Korean), J. Acoust. Soc. of Korea, 27, 140-148 (2008).

Y.-H. Choi, K.-C. Shin, J.-S. You, J.-S. Kim, W.-H. Joo, Y.-H. Kim, J.-H. Park, S.-M. Choi, and W.-S. Kim, "Numerical modeling and experimental verification for target strength of submerged objects" (in Korean), J. Ocean Eng. Technol. 19, 64-70 (2005).

H. G. Schneider, R. Berg, and L. Gilroy, "Acoustic scattering by a submarine: results from a benchmark target strength simulation workshop," Proc. 10th Int. Congr. Sound Vib, 1-8 (2003).

M. Nihof, L Fillinger, L. Gilroy, J. Ehrlich, and I. Schafer, "BeTSSi II : submarine target strength modelin workshop," Proc. 4th UACE, 377-384 (2017).

H. Cox, Fundamentals of bistatic active sonar. Underwater acoustic data processing, Springer Sci. Rev. 161, 3-24 (1989).

10.1007/978-94-009-2289-1_1

D. M. Fromm, J. P. Crocket, and L. B. Palmer, "BiRASP - The bistatic range-dependent active system performance prediction model," NRL, 1996.

M. Swift, J. L. Riley, S. Lourey, and L. Booth, "An review of the multistatic sonar program in australia," Proc. 5th ISSPA, 1 (1999).

Y.-S. Choo, S.-H. Byun, Y. Choo, and G. Choi, "Comparison of target classification accuracy according to the aspect angle and the bistatic angle in bistatic sonar" (in Korean), J. Acoust. Soc. Kr. 38, 511-521 (2011).

Y. H. Ji, H. S. Bae, G.-H. Byun, J. S. Kim, W.-S. Kim, and S. Park, "Investigation of target echoes in multi-static SONAR system - part II : numerical modeling with experimental verification" (in Korean), J. of Ocean Eng. & Tech. 28, 440-451(2014).

10.5574/KSOE.2014.28.5.440

C. Liu, M. Zhang, and W. Lin, "Calculation of bistatic scattering from underwater target with physical acoustic method," Procedia Eng. 15, 2561-2565 (2011).

10.1016/j.proeng.2011.08.481

D. Klement, J. Preissner, and V. Stein, "Special problems in applying the physical optics method for backscatter computation of complicated objects," IEEE Trans. Ant. Prop. 36, 228-237(1988).

10.1109/8.1100

Acoustics Module User's Guide, COMSOL Multiphysics v. 6.1 COMSOL AB, Stockholm, Sweden (2022).

The Journal of the Acoustical Society of KoreaISSN:1225-4428(Print) 2287-3775(Online)한국음향학회

Preview

Submarine bistatic target strength analysis based on bistatic-to-monostatic conversion

ABSTRACT

MAIN

(1)

(2)

Fig. 1.

(Color available online) Cartesian coordinates for acoustic wave scattering problem of underwater target.

(3)

(4)

(5)

(6)

Fig. 2.

(Color available online) Visible and invisible surfaces from source and receiver.

(7)

(8)

(9)

(10)

Fig. 3.

(Color available online) Bistatic target strength analysis procedure based on bistatic to monostatic conversion using equivalent-path length based virtual scattering surface.

Fig. 4.

(Color available online) Virtual scattering surface concept.

Fig. 5.

(Color available online) Moving vector calculation of scatter on target surface.

(11)

(12)

Fig. 6.

(Color available online) Numerical analysis model : BeTSSi.

Table 1.

Numerical analysis condition.

Fig. 7.

Bistatic target strength of BeTSSi (@100 Hz).

Fig. 8.

Bistatic target strength of BeTSSi (@500 Hz).

Fig. 9.

Bistatic target strength of BeTSSi (@1,000 Hz).

Fig. 10.

Bistatic target strength of BeTSSi (@1,500 Hz).

Fig. 11.

Bistatic target strength of BeTSSi (@2,000 Hz).

Acknowledgements

References