I. 서 론
II. 제안하는 시스템 구조
2.1 전체 시스템 구조
2.2 요소 신경망 구조
2.3 음향 구간 검출 신경망 구조
2.4 요소 신경망 결합 및 후처리
III. 학습 과정
3.1 전체 학습 과정
3.2 비표기 데이터의 학습: 평균-교사 모델
IV. 성능 평가
V. 결 론
I. 서 론
최근 기계 학습 기법이 크게 발전함에 따라, 이를 이용하여 인간의 일상 생활에 도움을 줄 수 있는 방법에 대해 여러 연구가 진행되고 있다. 이를 위하여 기계가 여러 종류의 입력 신호들을 이용하여 현재의 상황을 인식하거나 특정 이벤트를 검출하는 등의 연구가 진행되고 있으며, 특히 입력 신호가 음향 신호인 경우 위의 과업을 수행하도록 기계를 학습시키는 문제들이 음향 환경 인식[1] 혹은 음향 이벤트 검출[2]과 같은 문제로 정의되어 연구되고 있다. 음향 환경 인식 문제의 경우 상대적으로 긴 특정 음향 신호를 특정 환경으로 분류하는 문제를 주로 다루고 있으며, 음향 이벤트 검출 문제의 경우 음향 신호 내에서 상대적으로 짧은 음향 이벤트를 검출하는 문제로서, 이벤트의 종류 뿐 아니라 시작 혹은 종료 시점까지 함께 검출하는 특징을 가지고 있다. 따라서 음향 이벤트 검출 문제의 학습 데이터는 각 이벤트의 종류, 시작 시점, 종료 시점이 정답으로 제공된다.
여러 분야에서 기계학습 알고리즘이 좋은 성능을 보이고 있는 것이 사실이나, 다양한 환경에서 실용적인 성능을 얻기 위해서는 학습 데이터를 충분히 확보해야하며, 이는 기계학습 문제에서 풀기 어려운 숙제로 남아있다. 이러한 단점을 해결하기 위한 방법 중 하나로, 최근에는 정보의 일부만이 제공되는 학습 데이터를 이용하는 약지도 문제에 대한 연구가 이루어지고 있다.
특히 음향 이벤트 검출 문제에 대해서는 Detection and Classification of Acoustic Scenes and Events(DCASE) 2019에서 다음과 같은 약지도 문제가 제시된 바 있다.[3] 제공되는 학습데이터는 크게 3 종류이며, 첫 번째 데이터셋은 강하게 표기된 합성 데이터로, 이벤트의 종류, 시작, 종료 시점이 모두 제공되지만 실제 녹음된 데이터가 아니라 인위적으로 합성된 데이터이고 데이터의 수도 제한적이다. 두 번째 데이터 셋은 약하게 표기된 데이터로, 실제 환경에서 녹음된 데이터이지만 각 오디오 클립에 포함된 이벤트의 종류만 제공되고 시작, 종료 시점이 제공되지 않는다. 세 번째 데이터셋은 표기되지 않은 데이터로, 녹음된 데이터 및 인터넷 상의 여러 데이터를 포함하고 있으며, 데이터의 양은 많으나 아무런 정보가 표기되어 있지 않다. 이와 같이 제한된 정보를 가지고 검출 시스템을 구축하는 것이 약지도 음향 이벤트 검출 문제로 다루어지고 있다.
한편, 전통적으로 기계학습 시스템은 각 데이터의 특성을 잘 나타낼 수 있는 특징 값을 수동으로 추출한 후, 특징 벡터를 기반으로 원하는 결과를 만들어내는 네트워크를 학습시키는 단계로 구성되어 있다. 그러나 최근에는 특징을 수동으로 추출하지 않고 입력 신호로부터 원하는 결과까지의 과정을 모두 기계 학습에 의존하는 종단간(end-to-end) 학습 또한 연구가 진행되고 있다. 종단간 학습은 영상 처리 분야에서 더욱 활발히 연구되고 있지만, 음악 정보 처리[4] 혹은 환경음 학습[5] 등의 음향 신호 처리 관련 주제에 대해서도 최근 연구된 바 있다.
종단간 학습의 경우 특징을 추출하는 과정에서 발생되는 여러 요인들이 성능에 부정적인 영향을 미치는 것을 방지할 수 있는 장점이 있다. 전통적으로 음향 신호를 이용하여 기계 학습을 이용하는 경우 멜주파수 켑스트럼 계수 혹은 멜주파수 스펙트럼,[6],[7] 로그-멜주파수 에너지,[8] 혹은 일정 Q 변환(constant-Q transform)[9] 등의 특징 값들을 사용해온 바 있다. 이러한 경우 주파수 빈(bin)의 개수 및 프레임의 길이 등 적절한 특징 값을 추출하는 데에 영향을 주는 여러 요인들이 존재하게 된다. 시간 축의 음향 파형을 입력으로 받는 종단간 신경망을 구성할 경우 이러한 요인들을 배제할 수 있다.
위의 상황을 고려하여, 본 연구에서는 “약지도 음향 이벤트 검출” 문제를 “종단간 학습” 형태로 다루는 신경망 구조에 대해 연구하고자 하였다. 본 연구에서 도출한 시스템은 SampleCNN[4] 구조를 기반으로 하고 있으며, 이를 음향 이벤트 검출 문제에 적용하도록 짧은 길이의 여러 시간축 프레임을 파이프라인 형태로 적용할 수 있도록 변형하였다. 또한, 약지도 환경에 적합하도록 약하게 표기된 데이터 및 표기되지 않은 데이터를 처리하는 단계를 구성하고, 최근의 딥러닝 구조를 참고하여 도약 연결(skip connection) 및 게이팅(gating) 메커니즘 등의 추가적인 모듈을 이용하여 구조를 변형하였다. 그리고 음향 구간 검출(Sound Activity Detection, SAD) 및 기타 후처리를 이용하여 성능을 향상시키고자 하였다.
II. 제안하는 시스템 구조
2.1 전체 시스템 구조
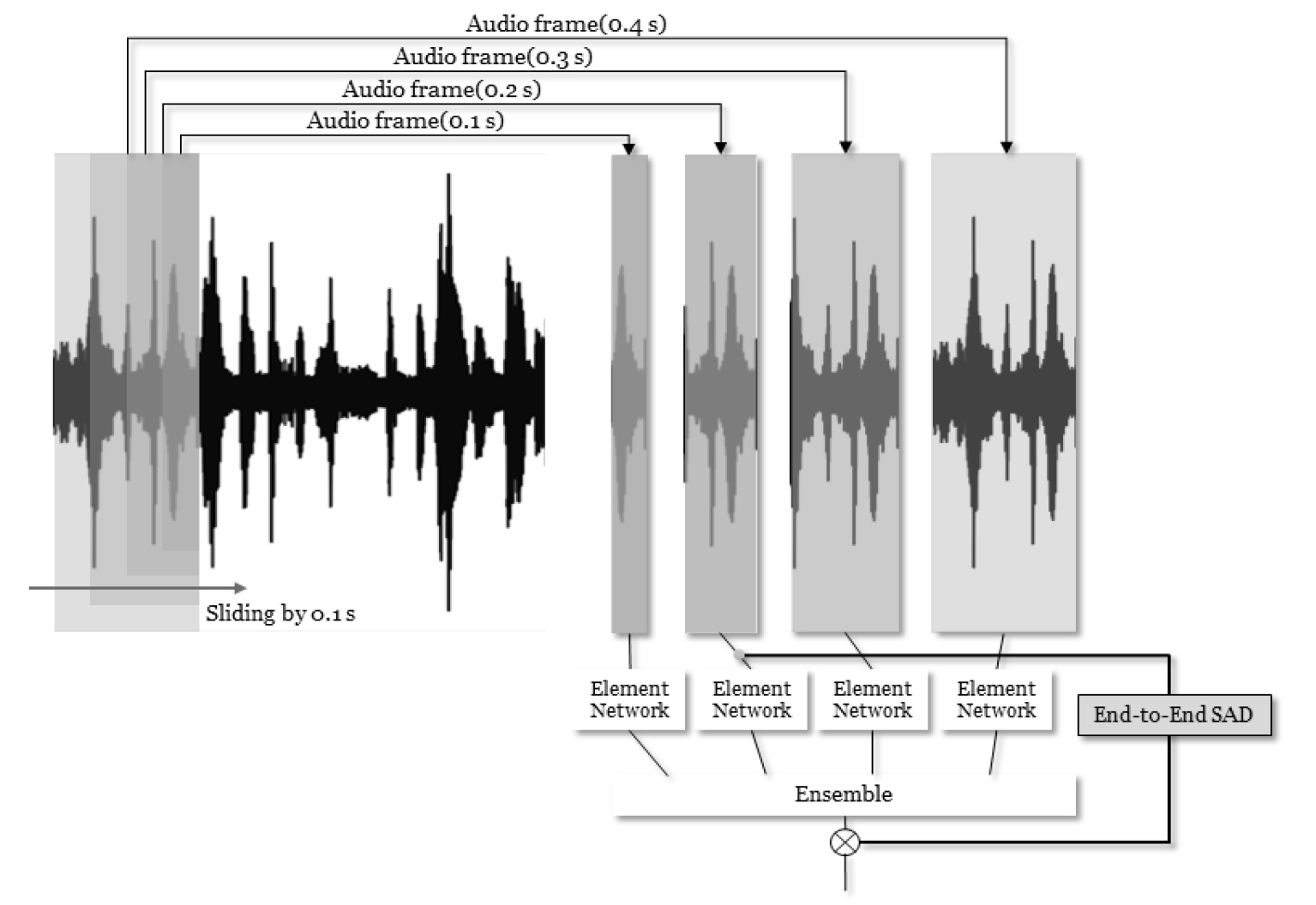
전체 신경망 구조는 Fig. 1과 같다. 기존의 sample CNN[4] 연구에서 보는 바와 같이 신호를 효과적으로 분류하기 위해서는 일정 길이 이상의 신호가 입력되어야 한다. 그러나 음향 이벤트 검출 문제에서는 신호의 시작 및 종료 시점을 검출해야 하고, 이를 위해 충분한 분해능이 요구된다. 이를 만족시키기 위하여 본 논문에서 제안하는 시스템은 여러 길이의 프레임을 사용하되, 이를 짧은 시간 단위로 슬라이딩함으로써 분해능을 확보하고자 하였다. 본 논문에서 제안하는 시스템에서는 4 종류의 프레임(0.1 s, 0.2 s, 0.3 s, 0.4 s)을 사용하였으며, 이를 0.1 s 단위로 슬라이딩하여 적용하였다(Fig. 1 참조).
각 프레임의 신호들은 요소 신경망(Fig. 1의 element network)의 입력 신호로 사용되며, 각 요소 신경망은 각 프레임의 입력 신호를 처리하여 각 음향 이벤트 종류의 활성화 확률을 출력 값으로 반환하게 된다.
각 음향 이벤트 별 확률 값은 각 요소 신경망의 출력 값을 이벤트 종류 별로 평균값을 계산하여 얻어지며, 이 결과에 음향 구간 검출 모듈의 출력을 곱한 후 후처리를 통해 음향 이벤트 검출을 수행하게 된다.
2.2 요소 신경망 구조
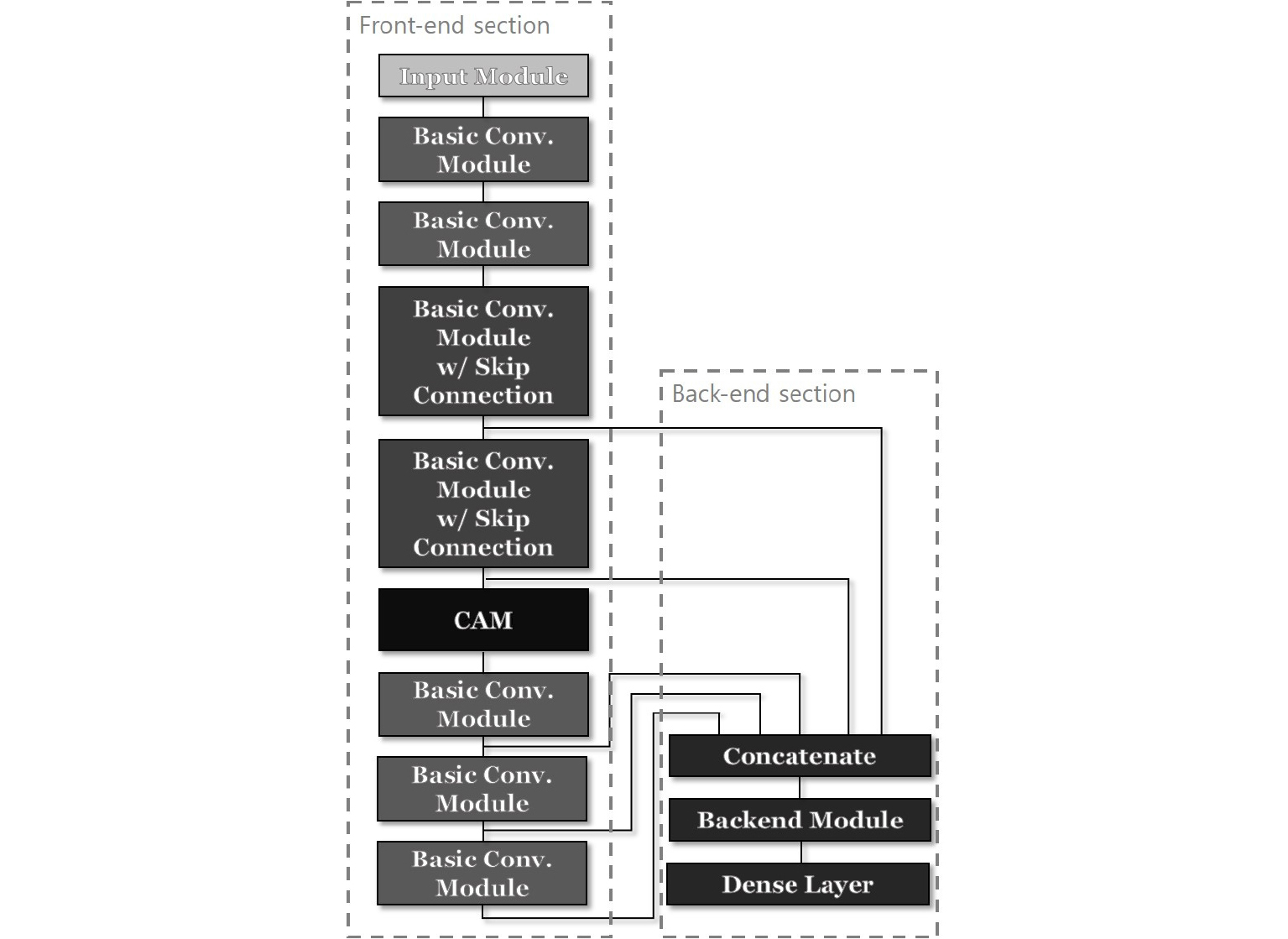
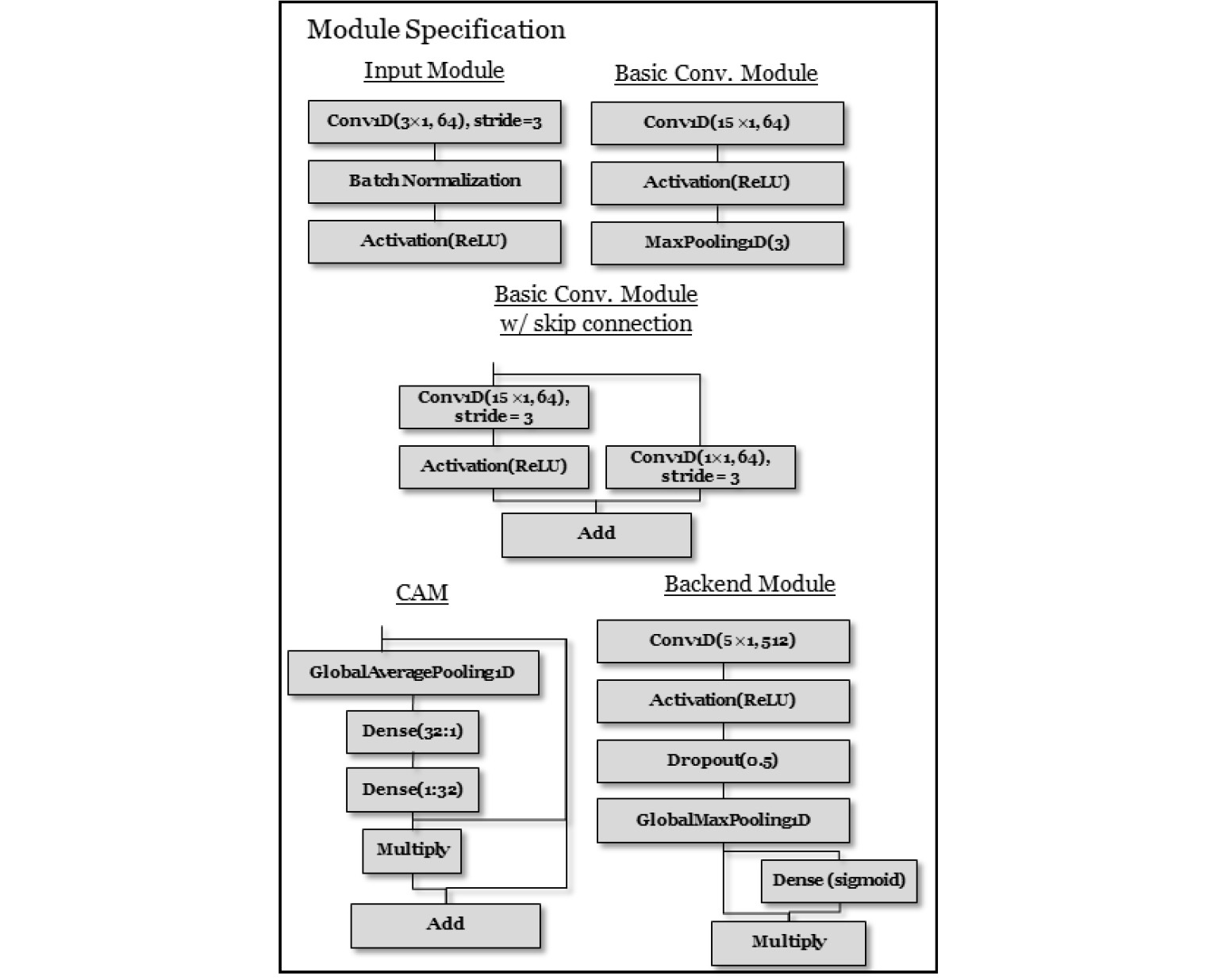
각 요소 신경망은 Fig. 2와 같은 구조로 구성되었으며, 요소 신경망 내 각 모듈의 세부 형태는 Fig. 3에서 확인할 수 있다. 요소 신경망은 음향 이벤트의 특징을 학습하는 전단부(front-end)와 이벤트를 분류하는 후단부(back-end) 구조로 이루어져 있다.
요소 신경망에서 가장 많은 부분을 차지하는 기본 콘볼루션 모듈은 1D-CNN과 최댓값 풀링 모듈로 이루어져있다. 이는 sampleCNN[4]의 구조를 기반으로 하여 구성되었으나, Reference [4]의 구조는 각 1D-CNN 사이에 모두 배치 정규화(batch normalization) 모듈이 존재하는 것과 달리, 본 논문의 구조에서는 입력 레이어를 제외한 모든 구간에서 정규화 모듈이 제거되었다. 이는 실험 결과 배치 정규화 모듈을 제거하였을 때 성능이 더욱 향상되는 경향을 보임에 따른 것이다.
또한, 3, 4번째 1D-CNN 레이어에는 Figs. 2와 3에서 보는 바와 같이 도약 연결(skip connection)이 추가로 구성되었으며, 이는 최근의 ResNet[10] 등의 구조에서 신경망이 깊게 형성된 경우 도약 연결이 성능 향상에 기여할 수 있다는 연구 결과에 착안하여 구성되었다.
4번째와 5번째 1D-CNN 모듈 사이에는 콘볼루션 어텐션 모듈(Convolutional Attention Module, CAM)이 자리잡고 있으며, 이는 기존의 이미지 처리에서 사용된 바 있는 콘볼루션 블록 어텐션 모듈[11]의 채널 어텐션 부분을 기반으로 하여 고안되었다. 해당 모듈은 병목 구조와 sigmoid 함수 기반의 활성화 함수를 통해 파라미터의 차원을 줄이는 역할을 한다.
후단부 구조는 3 ~ 7번째 1D-CNN의 출력을 결합한 후, 이를 특징값으로 삼아서 각 오디오 프레임의 클래스 확률 값을 출력하는 구조로 되어 있다. Figs. 2와 3에서 볼 수 있는 바와 같이, 후단 모듈은 1D-CNN과 최댓값 풀링으로 이루어져 있으며, 최대값 풀링은 각 채널 별 대푯값을 추출하는 역할을 한다. 풀링 모듈을 통해 선정된 값은 sigmoid 활성화 함수를 가지는 밀집 레이어의 결과에 의해 곱해지며, 이는 풀링 모듈의 결과 값을 중요도에 따라 가중치를 부여하는 게이팅 메커니즘의 역할을 한다.
후단부 구조의 결과 값은 하나의 밀집 레이어와 sigmoid 활성화 함수로 구성된 출력 레이어로 입력되며, 출력 레이어의 결과 값의 개수는 이벤트 종류의 개수와 동일하다.
2.3 음향 구간 검출 신경망 구조
본 논문에서 제안하는 시스템은 주파수 변환 등을 사용하지 않는 종단간 구조를 구축하는 것을 목표로 하고 있으므로, 음향 구간 검출 신경망 또한 입력 오디오 파형을 그대로 사용하는 신경망을 구축하는 것이 바람직하다. 본 시스템에서는 이러한 목적에 적합한 vadnet[12]의 구조를 적용하여 음향 구간 검출 신경망을 구성하였으며, 세부적인 구조는 Fig. 4에서 보는 바와 같다.
2.4 요소 신경망 결합 및 후처리
Fig. 1에서 볼 수 있는 바와 같이, 각 요소 신경망의 이벤트 종류 별 출력 값들은 하나의 값으로 결합되는 과정을 거치게 된다. 결합의 방법으로 투표 혹은 평균값 방법 등을 적용해 보았으나, 실험 결과 평균값의 성능이 더 좋은 경향을 보임에 따라 평균을 계산하여 취하는 방법으로 결정하였다.
각 요소 네트워크의 결합된 출력은 음향 구간 검출 신경망에 의해 통과 혹은 차단된다. 음향 구간 검출 신경망의 출력은 2 × 1 크기의 벡터로 구성되어 있으며, 첫 번째 원소는 신호가 없을 확률, 두 번째 원소는 신호가 있을 확률을 나타낸다. 즉, 각 출력 값을 특정 문턱값을 이용하여 이진화할 경우 신호가 없는 경우 [1 0], 신호가 있는 경우 [0 1]과 같이 원-핫 인코딩(one-hot encoding) 형태를 가진다. 따라서, 각 요소 신경망의 출력 평균을 이라 할 때, 전체 신경망의 출력 는 다음과 같이 계산된다.
여기서 는 음향 구간 검출 신경망 출력의 2번째 요소를 나타내며, 는 음향 구간 검출 문턱값을 나타낸다. Sigmoid 함수의 특성을 고려할 때 문턱 값으로는 중간 값인 0.5를 사용하는 것이 보편적이나, 본 실험에서는 0.4의 문턱값을 사용하였을 때 성능이 보다 좋아지는 결과를 얻어서, 여기서는 0.4의 값을 사용하였다.
위와 같이 계산된 각 이벤트 종류 별 확률 값을 이용하여 존재 여부를 판별하는 단계에서는 이중 문턱값 방법을 이용하였다. 이는 기존의 음향 이벤트 검출 기법에서 종종 사용되는 방법으로,[13] 먼저 높은 문턱값으로 음향 이벤트의 존재 유무를 판별한 뒤, 각 이벤트 별 존재 구간의 전/후에 낮은 문턱값을 적용하여 이를 확장하는 방법이다.
또한, 진공 청소기 소리 등과 같이 평균적으로 긴 길이를 가지는 이벤트 종류에 대해서는 추가적으로 최소 구간 / 간격 보상을 수행하였다. 이는 미리 설정된 최소 구간 / 간격 문턱 값과 각 신호 존재 구간 및 간격을 비교하여 문턱 값보다 작은 경우 이를 제거하는 방법으로, 기존의 음향 이벤트 검출 기법에 일부 적용된 바 있다.[14]
III. 학습 과정
3.1 전체 학습 과정
강하게 표기된 데이터, 약하게 표기된 데이터, 그리고 미표기 데이터를 모두 포함하는 약지도 학습 데이터에 대하여, 제안된 시스템은 다음과 같은 학습 과정을 거친다.
1) 강하게 표기된 데이터를 이용하여 음향 구간 검출 신경망을 학습시킨다. 이 때, 음향 구간 검출 신경망의 정답 레이블은 다음과 같이 설정된다.
여기서 와 는 각각 번째 프레임의 음향 구간 검출 신경망 및 강하게 표기된 데이터의 레이블을 의미한다.
2) 강하게 표기된 데이터와 약하게 표기된 데이터를 이용하여 각 요소 네트워크를 학습시킨다. 이 때, 약하게 표기된 데이터의 레이블은 음향 이벤트의 종류만 표기되어 있고 구간은 표기되어 있지 않으므로, 1)에서 학습시킨 음향 구간 검출 신경망을 이용하여 구간을 미리 추정한다.
3) 위에서 학습된 신경망을 이용하여 평균-교사 모델[15]을 구성한 후 비표기 데이터를 학습시킨다.
3.2 비표기 데이터의 학습: 평균-교사 모델
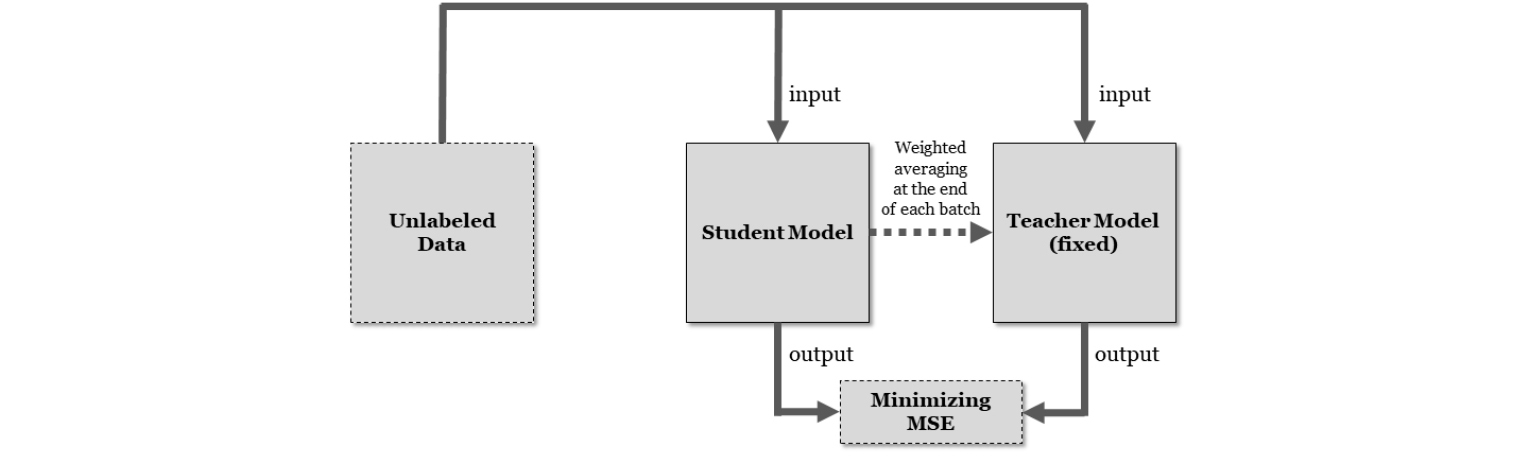
본 연구에서 비표기 데이터를 이용하여 모델을 학습시키기 위하여, Fig. 5와 같은 평균-교사 모델을 구성하였다. 학생 모델과 교사 모델 모두 2)의 학습 단계에서 학습된 모델로 초기화 되며, Fig. 5에서 보는 바와 같이 학생 모델은 일반적인 기계학습 과정과 같이 파라미터가 학습되고, 교사 모델의 파라미터는 고정되어 학습되지 않는다. 교사 모델의 파라미터는 각 배치의 학습이 끝나는 경우 다음과 같이 갱신된다.
| $$\theta_{teacher}\leftarrow\alpha\theta_{teacher}+(1-\alpha)\theta_{student},$$ | (3) |
여기서 및 는 각각 교사 모델 및 학생 모델의 신경망 파라미터를 나타내며, 는 누적 계수로 0과 1 사이의 값을 가진다.
IV. 성능 평가
제안하는 알고리즘의 성능을 평가하기 위하여, DCASE 2019 Task 4[3]의 개발 데이터셋을 이용하여 시뮬레이션을 진행하였다. 해당 데이터셋의 훈련 데이터는 2,045개의 강하게 표기된 데이터 파일, 1,578개의 약하게 표기된 데이터 파일, 그리고 14,412개의 비표기 데이터 파일로 구성되어 있다. 각 오디오 파일은 44,100 Hz의 샘플링 주파수를 가지는 10 s 길이의 오디오 파일이다. 해당 데이터 셋은 10 종류의 오디오 이벤트(음성, 강아지 소리, 고양이 소리, 알람/벨, 설거지, 튀기거나 굽는 소리, 블렌더, 물 소리, 진공청소기, 전기면도기/칫솔)로 구성되어 있다. 평가 데이터 셋은 1168개의 오디오 파일로, 훈련 데이터 셋과 중복되지 않는다.
후처리 단에서의 이중문턱값 중 낮은 문턱 값은 평가 데이터 셋의 이벤트 종류 별 확률 값의 평균과 표준편차를 더한 값으로 설정하였으며, 높은 문턱 값은 모든 클래스에 동일 수치를 적용하는 경우 0.55, 클래스 별로 독립적인 수치를 적용하는 경우 0.5 ~ 0.7 사이에서 성능이 좋게 나오는 수치를 적용하였다(Table 1 참조). 모델을 학습할 때에는 10-4의 학습율을 가지는 Adam[16]기법을 사용하였으며, 평균-교사 모델의 누적 계수 는 0.9999의 값을 사용하였다. 최소 구간 / 간격 보상은 이벤트 길이가 긴 이벤트 종류(Table 1의 Frying ~ Electric_Shaver의 5개 종류)에 대해 1초 미만의 구간 / 간격 보상을 수행하도록 설정하였다.
Table 1. Class-wise threshold values.
| Speech | Dog | Cat | Alarm bell |
| 0.65 | 0.55 | 0.5 | 0.6 |
| Dishes | Frying | Blender | Running water |
| 0.5 | 0.7 | 0.65 | 0.6 |
| Vacuum | Electric shaver | ||
| 0.7 | 0.7 |
의 값이 성능에 크게 영향을 미치지는 않았으나, 이 값이 큰 경우 평균-교사 모델에 의한 성능 향상이 줄어드는 경향을 보였고, 반대로 값이 작은 경우 성능이 저하되는 경향을 보였다. 이는 의 값이 큰 경우 평균-교사 모델에 의한 학습이 잘 일어나지 않아서 이득이 작아지는 것으로 추정되며, 반대로 의 값이 작은 경우 정답이 제대로 주어지지 않아 발생하는 오류에 의한 영향이 커지는 것으로 판단된다.
성능을 평가하기 위한 지표로는 F1-score를 사용하였다. F1-score는 다음과 같이 검출된 이벤트 중 정답에 해당하는 정확도 와 전체 정답 중 검출된 이벤트에 해당하는 재현율 의 조합으로 계산된다.
| $$P=\frac{n_{TP}}{n_{TP}+n_{FP}}.$$ | (4) |
| $$R=\frac{n_{TP}}{n_{TP}+n_{FN}}.$$ | (5) |
| $$F_1=\frac{2RP}{R+P},$$ | (6) |
여기서 는 검출된 정답, 는 검출된 오답, 는 검출되지 않은 정답의 개수를 의미한다. F1-score는 구간 단위 및 이벤트 단위로 분석되었으며, 구간 단위 F1-score는 1 s 단위의 구간 별로 검출 및 정답 여부를 검사하였다. 이벤트 단위 F1-score는 각 이벤트 별로 시작과 끝 지점을 정확히 맞추었는지 여부를 검사하되 0.2 s 범위 내(끝 지점의 경우 0.2 s 혹은 신호 길이의 20 % 이내) 에서 정답과 일치해야 정답을 맞힌 것으로 간주하였다. 위 결과 분석 조건은 DCASE 2019 Task 4의 조건과 동일하다.
Table 2 에는 요소 신경망 및 결합된 신경망, 그리고 평균-교사 모델을 적용하여 미표기 데이터를 학습시킨 후의 성능이 표시되어 있다. 여기서 SAD thresholding은 Eq. (1)에서 기술한 바와 같이 SAD 문턱 값으로 출력을 이진화 한 것을 의미한다. 요소 신경망의 성능에 비해 결합된 신경망 및 평균-교사 모델의 성능이 향상된 것을 확인할 수 있으며, 특히 이벤트 기반의 성능 지표의 경우 요소 신경망 대비 결합된 신경망의 성능이 크게 향상된 것을 확인할 수 있다. 이는 음향 구간 검출 신경망에서 아무런 이벤트가 없는 부분의 확률 값을 제거함으로써 이중 문턱값 후처리의 성능을 높여준 것이라고 생각된다.
Table 2. Simulation results of the element network, ensemble of 4 element networks and applying the SAD thresholding, and the improved network by training the unlabeled data with mean-teacher model.
| Segment-based (F1-score) | Event-based (F1-score) | |
| Element network with 0.2 s frames | 49.8 | 17.7 |
| Ensembled network w/ SAD thresholding | 52.4 | 30.7 |
| Applying the mean-teacher model | 54.3 | 31.8 |
Table 3은 각 후처리 방법에 따른 성능을 비교하여 보여주고 있다. 모든 클래스에 동일한 문턱값을 적용한 경우의 성능에 비해 클래스 별로 독립적인 문턱값을 적용한 경우의 성능이 더 향상된 것을 확인할 수 있다. 문턱 값이 특정 데이터 셋에 특화된 성능을 보이는지 여부를 확인하기 위하여, DCASE 2019 Task 4의 개발 데이터에 적용된 클래스 별 문턱값을 DCASE 2018 Task 4의 평가 데이터에도 적용해 보았으며, 그 결과 DCASE 2018 Task 4의 데이터에서도 유사한 성능 개선을 확인할 수 있었다. 또한, 최소 구간 / 간격 보상의 경우 성능에 긍정적인 영향을 주었음을 확인할 수 있으며, 특히 이벤트 단위의 성능을 크게 향상시킨 것을 확인할 수 있다.
Table 3. Performance comparisons of the various post processings (DCASE 2019 Dev. / DCASE 2018 Eval.).
V. 결 론
본 논문에서는 심층 콘볼루션 신경망을 기반으로 하는 약지도 음향 이벤트 검출 시스템을 구축하고 이에 대한 성능 평가를 진행하였다. 특히, 본 논문에서는 시간 축 파형을 입력으로 하여 최종 결과를 도출하는 종단간 구조를 가지는 시스템을 구축하고자 하였다. 구축된 시스템은 sampleCNN의 구조를 기반으로 하여 도약 연결, 어텐션 메커니즘 등을 추가로 구축하였으며, 평균-교사 모델을 적용하여 미표기 데이터를 학습에 활용하도록 하였다.
또한, DCASE 2019 Task 4의 개발 데이터 셋을 이용하여 성능 평가를 위한 시뮬레이션을 진행하였다. 그 결과 고안된 시스템이 약 54.3 %의 구간 단위 F1- score와 31.8 %의 이벤트 단위 F1-score의 성능을 보임을 확인할 수 있었다.