I. Introduction
II. Proposed Approaches
2.1 Combining MTAE-WGAN-GP
2.2 Initialization of weights for leaky and parametric rectified linear unit
III. Experimental Setup
3.1 Dataset
3.2 Preprocessing
IV. Results
4.1 Experiment 1
4.2 Experiment 2
V. Conclusions
I. Introduction
With rapid advancement of deep learning, acoustic event recognition and Automatic Speech Recognition (ASR) technologies have been widely used in our daily lives such as in intelligent virtual assistants, mobile devices and other electronic devices. However, presence of various types of noise in speech or intended acoustic signal degrades the performance of such recognition systems. Speech enhancement is considered a very crucial technique because it can reduce the impact of noise and improve recognition accuracy. There have been many approaches such as traditional speech enhancement approaches include Wiener filter,[1] Short Time Spectral Amplitude-Minimum Mean Square Error (STSA-MMSE)[2] and nonnegative matrix factorization.[3] Deep learning approaches include Deep Denoising AutoEncoder (DDAE), Deep Neural Network (DNN),[4] Convolutional Neural Network (CNN),[5] or Recurrent Neural Network (RNN)[6] have been applied for speech enhancement in past few years, and they can be divided into a regression method (mapping-based targets)[1], [5], [7] and a classification method (masking-based targets).[8], [9] Although these methods have attained an acceptable level for speech enhancement, there is still room for improvement.
In recent years, Generative Adversarial Network (GAN) has been widely used across many applications of deep learning, from image generation[10] to video and sequence generation,[11], [12] and has achieved better performance. Speech Enhancement GAN (SEGAN) is the first GAN- based model used for speech enhancement.[13] GAN is considered hard to train and sensitive to hyper-parameters. Also, the training loss type (L1 or L2) affects the enhancement performance as it has been noticed by Pandey and Wang, where the adversarial loss training in SEGAN does not achieve better performance than L1 loss training.[14] In addition, Donahue, et al. proposed Frequency-domain SEGAN (FSEGAN)[15] for robust attention-based ASR system,[16] and achieved lower Word Error Rate (WER) than WaveNet[17] based SEGAN. Afterward, Michelsanti proposed a state-of-the-art CNN based Pix2Pix framework[18] and Mimura et al. proposed a Cycle-GAN-based acoustic feature transformation[19] for robust ASR model.
These studies using many kinds of GAN framework demonstrated improved performances for speech enhancement tasks. Nonetheless,[13], [15], [19] compared their methods with conventional methods. Therefore, it is hard to demonstrate the advantage of adversarial loss training over L1 loss training for speech enhancement. In this work, we illustrate the effectiveness of the adversarial loss training by comparing our proposed Multi-Task AutoEncoder- Wasserstein Generative Adversarial Network-Gradient Penalty (MATAE-WGAN-GP) and a single generator based on MTAE.[20] To summarize, our contribution is to propose an architecture that combines MTAE and Wasserstein GAN for separating speech and noise signals into one network. This structure combines the advantages of multi-tasking learning and GAN, and result in improving PER performance. We also propose a weights initialization method based on He[21] for Leaky Rectified Linear Unit (LReLU) and Parametric ReLU (PReLU). As a result, loss becomes more stable during learning process, thereby avoiding possible exploding gradients problem in a deep network.
In summary, by adopting GP loss function, our proposed integrated model (MTAE-WGAN-GP) achieves lower PER over other state-of-the-art CNN and RNN for robust ASR system. This paper is organized as follows. In Section II, we present the proposed model structure and weights initialization. We then describe the experimental settings in Section III. The results are discussed and evaluated in Section IV and finally, conclusions are provided in Section V.
II. Proposed Approaches
2.1 Combining MTAE-WGAN-GP
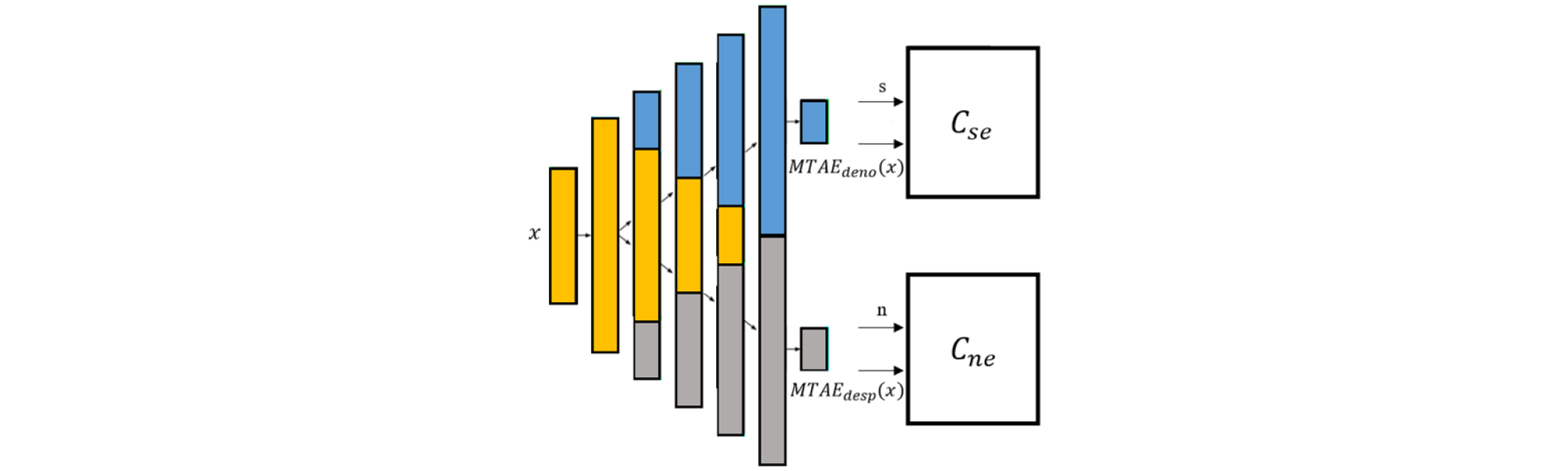
Our proposed MTAE-WGAN-GP is composed of one generator and two critics as shown in Fig. 1. The generator is a fully connected MTAE and is intended to produce estimates of not only speech but also noise from noisy speech input. Speech estimate critic () and noise estimate critic () are both fully connected DNNs, tasked with determining if a given sample is real ( and ) or fake [ and ]. After training, we use a single MTAE based generator for our speech enhancement task. The loss function for generator composed of adversarial loss and L1 loss is represented by
where and are the estimated speech and the target clean speech respectively. and are the estimated noise and the target noise respectively. , and are hyper-parameters. By experiment, we set = 0.5, = 100 and = 0.5 for the best performance in our system. Our model adopts Wasserstein distance as a continuous and almost differentiable function within the range restricted by 1-Lipschitz constraint. The loss function for the critics are represented by
The generator consists of 5 hidden layers and 1024 units were set in the first layer. Then, as described in[20] the denoising exclusive units, the shared units and the despeeching exclusive units for each layer from the 1st to the 5th are (0, 1024, 0), (256, 768, 256), (512, 512, 512), (768, 256, 768) and (1024, 0, 1024), respectively. Additionally, in[18] we modify term in Eq. (9) to with LReLU activation function as our weight initialization (subsection 2.2).
The critics feed as not only real and fake data but also the input data . The pairs are (, ) and (, ) for speech estimate critic, and (, ) and (, ) for noise estimate critic. The speech estimate critic network is composed of 4-layers with 1024, 768, 512, and 256 units, while the noise estimate critic is composed of 3-layers with 512 units per layer where both models use LReLU as activation function.
2.2 Initialization of weights for leaky and parametric rectified linear unit
Network parameter initialization plays a considerably significant part in the network training where inappropriate initialization could lead to poor results.[22] We briefly describe the initialization methods proposed by Xavier[23] and He,[21] and propose a modified initialization approach for LReLU and PReLU based activation. The method has been shown to be particularly effective when the number of network layers becomes large.
The response representation for DNN is:
| $$Y_l=W_lX_l+B_l.$$ | (4) |
| $$X_l=f(Y_{l-1}),$$ | (5) |
where and are weight and bias matrix. f is the activation and we use l to index a layer.
The idea of He initialization[21] is based on Xavier initialization[23] in that it preserves the same variance of the response input throughout the layers. As in,[23] by initializing the elements of to be independent and identically distributed (i.i.d.), we assume that elements are i.i.d. and both and are independent from each other. Then we can obtain:
| $$Var\lbrack y_l\rbrack=n_lVar\lbrack w_lx_l\rbrack,$$ | (6) |
where, , , and are random variables of elements in , , and , respectively. is the number of nodes. By setting to have zero mean, variance of the product of independent variables can be written as:
| $$Var\lbrack y_l\rbrack=n_lVar\lbrack w_l\rbrack E\lbrack x_l^2\rbrack.$$ | (7) |
Since ReLU function is not linear and does not have a zero mean, by initializing to have a symmetric distribution around zero and setting to zero, will also have a symmetric distribution with zero mean.[21] Thus, the expectation of xl can be written as: , when ReLU is used as an activation function.[21] However, in the case of LReLU or PReLU being used as an activation function, should be considered when is less than zero.
Suppose the activation function is a linear transformation with slope and zero intercept. Standard deviation () and variance of will become and respectively.
In the case of two different alphas from zero mean, such as LReLU, we can calculate the mean defined as:
| $$\begin{array}{l}E\lbrack x_l^2\rbrack=\frac{\alpha_{Positive}^2+\alpha_{Negative}^2}2Var\lbrack y_{l-1}\rbrack,\\,\;for\;all\;x_l\end{array}$$ | (8) |
where is the slope for , and is the slope for of LReLU or PReLU.
For LReLU or PReLU, is equal to 1. Thus, we can rewrite it as:
| $$E\lbrack x_l^2\rbrack=\frac{1+\alpha_{Negative}^2}2Var\lbrack y_{l-1}\rbrack,\;for\;all\;x_l.$$ | (9) |
By substituting Eq. (9) into Eq. (7), we obtain:
| $$Var\lbrack y_l\rbrack=\frac{1+\alpha_{Negative}^2}2n_lVar\lbrack w_l\rbrack Var\lbrack y_{l-1}\rbrack.$$ | (10) |
And with L layers, we get:
| $$Var[y _{L} ]=Var[y _{l} ]( \prod _{l=2}^{L} \frac{1+ \alpha _{Negative}^{2}} {2} n _{l} Var[w _{l} ]).$$ | (11) |
Finally, a sufficient condition is:
| $$\frac{1+ \alpha _{Negative}^{2}} {2} n _{l} Var[w _{l} ]=1, \forall l.$$ | (12) |
Therefore, the proposed initialization method in Eq. (12) leads to zero-mean Gaussian distribution and equal to where, b is initialized as zero. For the first layer ( = 1), the sufficient condition will be , since there is no activation function applied to the input. The initial value of for LReLU is set to 0.5 in this paper.
III. Experimental Setup
Two sets of experiments are conducted to evaluate our proposed model and initialization method. Firstly, we evaluate the effectiveness of proposed MTAE-WGAN- GP against state-of-the-art methods. Secondly, we compare the initial output variance and convergence of our proposed initialization against Xavier and He initialization.
3.1 Dataset
For training the proposed model, we used the Texas Instruments/Massachusetts Institute of Technology (TIMIT) training dataset which contains 3696 utterances from 462 speakers. The training utterance is augmented by 10 types of noise (2 artificial and 8 from YouTube.com: pink noise, red noise, classroom, laundry room, lobby, playground, rain, restaurant, river, and street). Each signal and background noise added together with three Signal to Noise Ratio (SNR) levels (5 dB, 15 dB, and 20 dB). The obtained dataset for training the proposed model contains 9 % of clean speech to ensure the effectiveness of the model even in clean environment. Wen has shown the effectiveness of using synthetic noise during training for speech enhancement task.[24]
TIMIT testing set that contains 192 utterances from 24 speakers is corrupted by 3 types of unseen noise (café, pub, and schoolyard), collected from ETSI EG 202 396-1 V1.2.2 (2008-09) with three different SNR levels (5 dB, 15 dB, and 20 dB). The augmentation for the dataset is conducted using ADDNOISE MATLAB.[25]
3.2 Preprocessing
Kaldi toolkit is used for training the ASR model using a Hybrid System (Karel’s DNN) on a clean TIMIT Acoustic- Phonetic Continuous Speech Corpus training data. The sampling rate for the audio signals was at 16 kHz and features are extracted by means of short-time Fourier transform with window size of 25 ms and 10 ms window step. Here, we applied 23 Mel-filter banks, with Mel-scale from 20 Hz to 7800 Hz.
The proposed model (MTAE-WGAN-GP) and MTAE were trained by setting the data with concatenated 16 contiguous frames of 13-dimensional MFCCs (13x16). The same data format was used to conduct both experiments. All features are normalized per utterance within the range of [-1, 1]. All networks are trained using Root Mean Square Propagation (RMSprop) optimizer with a batch size of 100. For DDAE and MTAE architecture LReLU activation function is used except in the output layer which has no activation function.
IV. Results
4.1 Experiment 1
DDAE vs. MTAE vs. RNN vs. CNN vs. MTAE- WGAN-GP
We adopt L1 loss for all used training models. DDAE,[26] MTAE,[20] Recurrent MTAE (RMTAE) and Redundant Convolutional Encoder-Decoder (R-CED)[5] are used as baseline models to compare performance of the proposed model in terms of PER. Hence, by incorporating a typical ASR model, performance is evaluated by measuring how well the system recognizes noisy speech after the speech enhancement. The RMTAE model consists of 3 LSTM layers followed by 2 fully-connected layers with 256 units and LReLU as activation function except for the output layer. To avoid exploding gradients problem, we use a gradient clipping from -1 to 1.[27] The results are reported in Table 1.
Table 1. Performance comparison between non-enhanced features (None), DDAE, RMTAE (RNN), CNN (R-CED) and MTAE-WGAN-GP on 3 types of unseen noise with three SNR conditions.
Table 1 reports the performance of these models. It can be observed that over three SNR conditions and three unseen noise, the proposed method consistently improved the recognition accuracy by 19.6 %, 8.1 %, 6.9 %, 3.6 %, and 1.8 % relative to non-enhanced features (None), DDAE, MTAE, R-CED (CNN) and RMTAE (RNN). Especially at low SNR scenarios, the improvement becomes more apparent. Additionally, we observe that at high SNR condition (20 dB) the RMTAE (RNN) has a competitive performance compare to our proposed method. However, performance is degraded obviously when SNR becomes lower (15 dB and 5 dB).
MTAE-WGAN-GP achieves lower PER compare to a single generator MTAE. This demonstrates the effectiveness of adversarial loss training is better than using L1 loss alone.
4.2 Experiment 2
Xavier initialization vs. He initialization vs. Our initialization
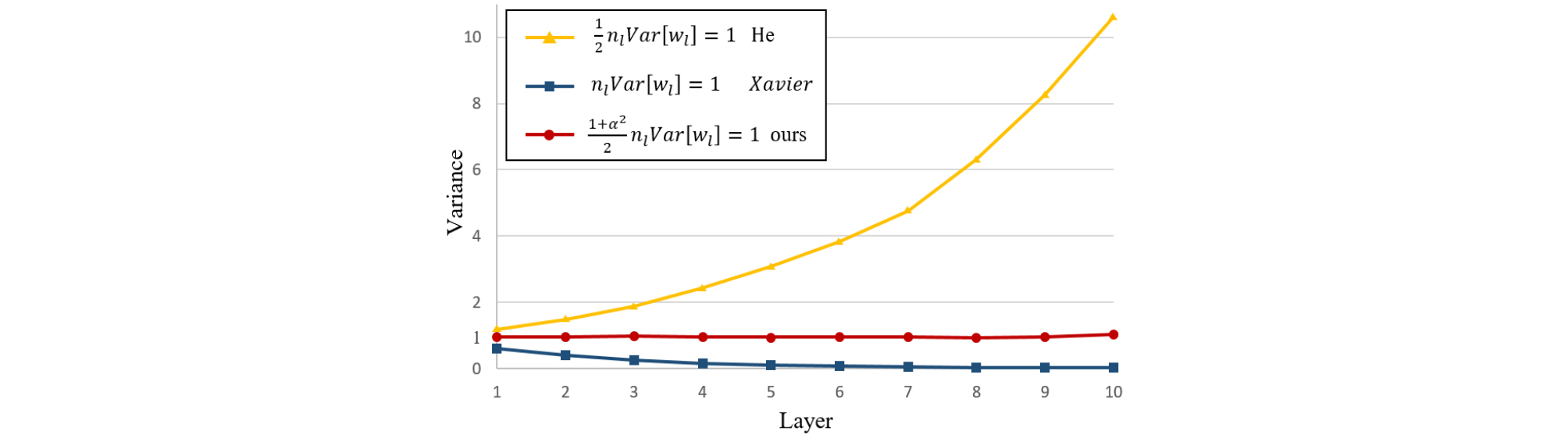
We adopt a 10 layer-MTAE to compare with Xavier[23] and He initialization.[21] By increasing units linearly, the denoising exclusive units, the shared units, and the de- speeching exclusive units are (0, 1200, 0) and (1200, 0, 1200) for 1st and 10th layers, respectively. Fig. 2 shows the histograms of the output distribution in each layer before training. We can observe that as the number of layers increases, the variance in He initialization increases dramatically while the variance in Xavier initialization gradually decreases toward zero. However, our proposed initialization keeps the output distribution and variance steady through each layer, as shown in Fig. 3.
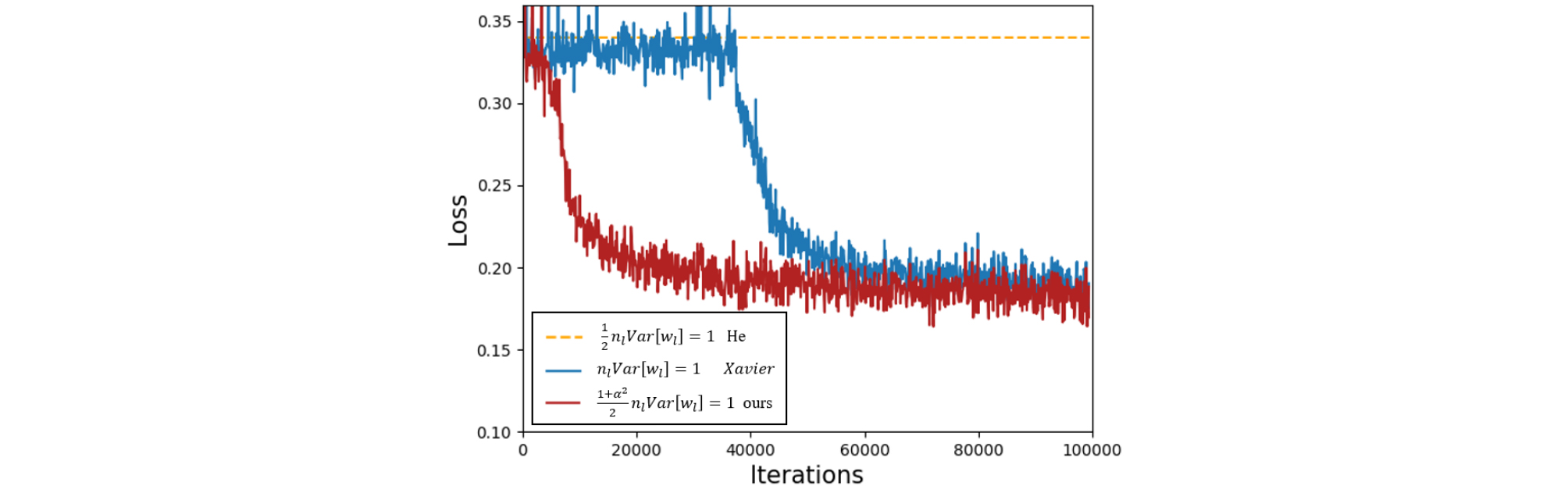
Next, we compare our proposed initialization with He and Xavier on a 25 layers MTAE using the obtained loss of the model. Fig. 4 shows the loss of convergence during training. We can observe that in training our proposed initialization converges faster and more stable than Xavier initialization, while He initialization cannot converge and can easily suffer from exploding gradient problem during training with deep network. This illustrates the advantage of using the proposed initialization when training a deep network with LReLU and PReLU.
V. Conclusions
We proposed MTAE-WGAN combination as an architecture that integrates MTAE with WGAN and demonstrated improvement in ASR performance. Additionally, we proposed an initialization of weights for LReLU and PReLU and demonstrated that it converges faster with more stable than Xavier and He initialization. The results show that MTAE-WGAN-GP achieves 8.1 %, 6.9 %, 3.6 %, and 1.8 % PERs improvement relative to DDAE, MTAE, R-CED (CNN) and RMTAE (RNN) model, respectively.