I. 서 론

능동형 소나 탐지 분야에서 사용되는 신호들 가운데 하나인 Linear Frequency Modulation(LFM) 신호는 주파수가 시간에 따라 선형적으로 변화하는 신호로 다른 신호나 잡음으로 인해 발생하는 간섭에 대해 내성을 갖는 장점이 있으며, 이는 주로 정합 필터에 의한 펄스 압축 효과 때문이다. 이로 인하여 이 신호는 소나 시스템뿐만 아니라 초음파 영상 취득 등과 같은 다양한 분야에서 사용되고 있으며, 특히 수중 이동체에 대한 시험평가 과정에서 거리 추정을 위해서도 적용될 수 있다.^[1]

소나나 레이더에서 거리 추정을 위해 도달 시간차(Time Difference-Of-Arrival, TDOA) 나 도플러 천이 주파수 추정 등에 기반한 방법들이 있으며,^[2,3,4] 이 가운데 송수신기 사이에 시간 동기화가 이루어져야 한다는 조건이 있기는 하지만 도달 시간(Time-Of-Arrival, TOA) 측정에 기반한 방법은 비교적 높은 정확도를 나타내는 것으로 알려져 있다.^[5] 이러한 도달 시간 측정을 위하여 LFM 신호를 사용할 수 있지만 송수신기 사이에 상대적인 이동성이 있는 환경에서는 신호의 주파수가 변화하는 도플러 효과도 고려해야 한다. 특히, 큰 도플러 주파수 변화는 정합필터 출력에서 첨두치 위치의 불일치를 유발하는데 이는 도플러 효과로 인한 주파수 변화와 거리 추정 사이에 상호 의존성이 발생하는 것으로써 거리-도플러 커플링 효과라고 한다.^[6,7] 따라서 LFM 신호를 사용하여 거리를 추정하는 경우 측정된 도달 시간 값에 편향이 발생하므로 거리 추정 오차를 유발하는 거리-도플러 커플링 효과를 고려하여야 한다. 실제로 거리 또는 위치와 속도의 조합에 따라 편향이 발생하는데 이러한 편향을 고려하여 적절한 보정이 필요하다.

이를 위해 Wang et al.^[8]은 수중 이동체의 속도에 의한 도플러 변이에 둔감하면서 하나의 주파수 대역에서 광대역 신호인 Hyperbolic Frequency Modulation(HFM) 펄스 두 개를 상반된 스윕 방향으로 연속적으로 연결하여 송신한 뒤 이 두 펄스 사이의 송신 시간 간격과 탐지시간 차이의 변화를 통하여 수중 이동체의 속도와 거리를 추정하였다. 또한 LFM 신호와 LFM 신호 또는 HFM 신호를 연접하여 적용하는 방안이 제시되기도 하였다.^[9,10] 최근에는 동일 주파수 대역에 있는 HFM 신호 사이의 상호상관성에 의한 탐지 성능저하를 방지하기 위하여 대역이 분리되어 있으면서 상반된 스윕 방향의 두 HFM 펄스를 이용하는 방법이 제안되었다.^[11] 하지만 이러한 기존의 방법들 대부분은 2종류의 주파수 변조 신호를 연접하여 구성한 형태로 상대적으로 긴 송신 시간을 가지며, 대역을 분리하는 경우 그만큼 대역폭이 좁아져서 수신단 처리 과정에서 상관 이득이 감소하는 문제점이 있다.

본 논문에서는 LFM 신호를 사용하는 거리 추정 문제에서 거리-도플러 커플링 효과로 인해 첨두치 위치가 변경되는 오차가 발생할 수 있는데 이러한 오차를 상쇄하고 편향이 없는 값을 찾을 수 있는 신호 형태를 제시한다. 제안된 신호는 상반된 스윕 방향을 갖는 2종류의 LFM 신호를 중첩하여 구성된다.

본 논문의 구성은 다음과 같다. 제 2장에서는 거리 추정 과정에서 LFM 신호 적용의 문제점을 제시하고, 제3장에서는 제안하는 방법을 서술한다. 제4장에서는 시뮬레이션을 위한 파라메타와 결과를 제시하며, 마지막으로 결론은 제5장에서 서술한다.

II. 거리 추정을 위한 LFM 신호

수중 이동체의 시험평가를 위해 고정된 수신기 사이의 거리를 추정하기 위해 처음에 수중 이동체에 장착된 송신기는 수신기와 동기화되고 이후 신호를 주기적으로 송신한다고 할 때 적용되는 LFM 신호는 다음과 같다.

여기서 f0는 시작주파수를 의미한다. T는 신호의 길이, B는 대역폭으로써 f0-f1과 같이 표현된다. 여기서 f1은 끝 주파수를 의미한다. 만약 f0-f1<0 인 상황에서는 시간-주파수 기울기가 상승 스윕인 +LFM 신호가 생성되며, f0-f1>0 이라면 하강 스윕인 –LFM 신호가 생성된다.

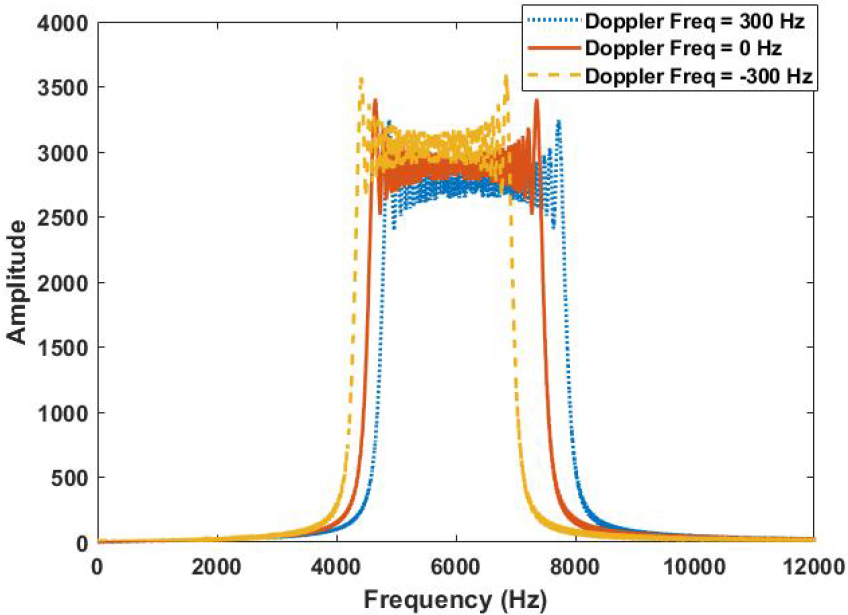
수중 이동체의 이동 속도가 증가하면 수신된 LFM 신호는 도플러 효과에 의해 영향을 받는다. 도플러 천이는 이동하는 대상에 의해 발생하는 주파수 변화를 의미하며, 이는 수신된 신호의 주파수에 영향을 준다. Fig. 1의 예시와 같이 도플러 천이는 주로 대상의 이동 속도에 비례하여 증가하며, 이는 수신된 LFM 신호의 주파수에 변화를 발생시킨다.

Fig. 1.

(Color available online) The effect of Doppler shift on the LFM spectrum.

c는 수중에서의 음속, v는 이동하는 송신기와 고정되어 있는 수신기 사이의 상대 속도로 가정한다면 도플러 스케일은 ∆=v/c로 정의되며, 스케일 팽창계수는 D=1+∆로 나타낼 수 있다. 도플러 주파수 천이가 더해져 수신된 신호는 다음과 같이 표현된다.

여기서 𝜏는 송신기와 수신기 사이의 거리에 따른 도달 시간차를 나타낸다.

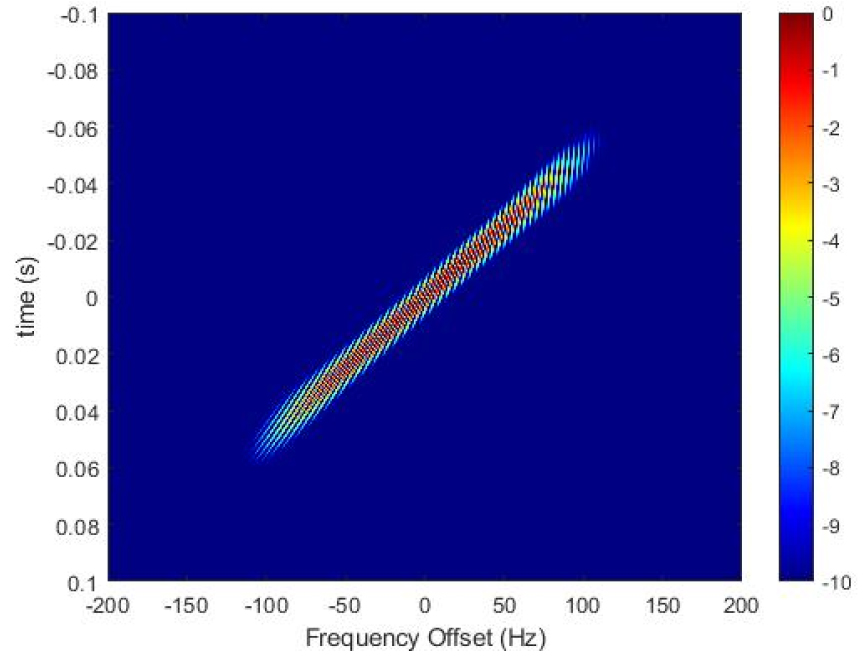
수신된 신호는 정합 필터링 과정을 거치는데 정합 필터링은 수신된 신호와 송신된 신호 사이의 정합을 통해 신호 처리 이득을 얻는 다. 하지만 Fig. 2에 나타낸 LFM 신호의 모호도의 예를 보면 시간-주파수 영역에서 기울어진 형태임을 볼 수 있으며, 이는 거리-도플러 커플링 효과가 발생한다는 것을 알려준다. 즉, 도플러 주파수 천이가 포함된 LFM 신호의 정합필터 출력은 천이된 주파수에 비례하여 시간 천이도 발생한다는 것이다.

Fig. 2.

(Color available online) Delay-Doppler ambiguity function of LFM signal.

수중 이동체와 수신기 사이에 상대적인 움직임이 있으면, 수신된 신호의 주파수는 상대적으로 높아지거나 낮아진다. 동시에 시간 영역에서는 신호가 압축 또는 팽창되는데 수중 이동체의 이동 속도가 증가할수록 LFM 신호의 정합 필터 출력에서 도플러 효과에 의한 시간 지연도 점차 증가한다. 이러한 현상을 Fig. 3의 예시에서 확인할 수 있다.

Fig. 3.

(Color available online) The correlation output of LFM signal.

따라서 LFM 신호를 수신할 때, 시간에 따라 주파수가 변화하므로, 신호의 주파수와 시간 지연을 함께 고려해야 한다. 정합 필터링을 사용하여 피크를 탐지하지만 그 피크 위치는 거리에 따른 도달 시간 차이뿐만 아니라 도플러 주파수 천이에 의한 시간적인 변화도 포함된다. 따라서 정합 필터링을 통해 얻은 첨두치의 위치로부터 도달 시간 정보만을 추출하기 위해서는 도플러 효과로 인한 변화를 고려하여 보정해야 한다. 정합필터링 후에 도플러 주파수 천이에 의해 발생하는 시간 지연 오차 t0는 다음과 같이 표현할 수 있다.^[12]

여기서 fd는 도플러 천이 주파수를 의미하며, 결국 이 도플러 천이 주파수를 알아야 정확한 도달 시간을 추정할 수 있다.

송신된 LFM 신호의 도달 시간을 유도하기 위해 기존의 방법처럼 +LFM 신호를 전송하고, 그 다음에 시간에 따라 주파수가 감소하는 –LFM 신호를 전송한다고 가정하자. 이러한 상황에서 두 신호를 수신하고, 각 신호에 대한 정합 필터링을 수행한다. 각 신호에 대한 정합 필터의 출력 값이 최대가 되는 시점을 구하면, 해당 시간은 각각 +LFM과 –LFM의 도착 시간을 다음과 같이 유도할 수 있다.

여기서 t-LFM은 –LFM 신호에 의해 정합 필터 출력의 최대값이 나타나는 시간을 나타내며, t+LFM 은 +LFM 신호에 의해 정합 필터 출력의 최대값이 나타나는 시간이다. 이때 T/D+2t0 은 +LFM과 –LFM 신호의 도착 시간 간격을 나타낸다. 이를 통해 +LFM과 –LFM 신호의 도착 시간을 상대적으로 유도할 수 있다. 도플러 효과에 의해 송신된 신호는 압축되거나 팽창되어 시간영역과 주파수 영역에서 변화하며 Fig. 4의 예시와 같이 나타난다. Fig. 4는 도플러 주파수 천이가 없을 때의 스펙트로그램과 +LFM과 –LFM 신호가 양(+)의 도플러로 인하여 신호가 압축되어 도플러 천이가 발생하였을 때의 스펙트로그램을 정합 필터 출력 값과 함께 비교한 결과의 예이다. 상단의 스펙트로그램을 보면 양(+)의 도플러 주파수 천이로 인하여 LFM 신호가 위쪽으로 이동하였고, LFM의 기울기도 변화하여 신호의 길이도 변화한 것을 볼 수 있다. 기울기의 변화는 B×D/T 와 같이 표현할 수 있다. 이러한 변화로 인하여 정합필터의 출력 값이 정답의 위치보다 시간 지연 오차가 발생하는 것을 볼 수 있으며, 첨두치의 위치 차이의 비율도 도플러 주파수 천이에 따라 변화하는 것을 볼 수 있다. 이러한 오차를 고려하여 적절한 보정이 필요하며, 보다 정확한 도달 시간 값을 추정하기 위하여 스케일 팽창계수 D의 변화를 추정하는 과정이 필요하다.

Fig. 4.

(Color available online) An illustration of the Doppler effect for up-and down-sweep LFM signal.

III. 제안한 방법

동기화된 송신기가 장착된 수중 이동체와 수신기 사이의 거리 추정을 위해 본 연구에서 제안하는 중첩된 LFM 신호의 구성 방법은 다음 Fig. 5의 스펙트로그램과 같다. 중첩된 LFM 신호는 +LFM과 –LFM 신호로 구성되며, +LFM과 –LFM의 주파수 대역은 겹치도록 설정된다. 즉, 두 신호의 주파수 대역이 서로 겹치도록 하며, 이렇게 중첩된 신호를 송신한다.

Fig. 5.

(Color available online) Spectrogram of a superimposed LFM signal.

수신단에서는 replica 신호로 사용하여 상관관계를 구하는데 replica 신호는 송신한 신호와 동일한 특성을 가지는 신호이다. 이러한 방법을 통해 도플러 효과로 인한 거리-도플러 커플링 현상이 발생하면, Fig. 6과 같이 두 개의 첨두치가 생성된다. 예를 들어 Fig. 4에서처럼, 양(+)의 도플러 주파수에 의해 주파수가 변화한 경우, +LFM 신호는 올바른 첨두치의 위치보다 더 왼쪽에 나타나게 된다. 반대로, 음(-)의 도플러 주파수가 신호에 더해진 경우, –LFM 신호는 올바른 첨두치의 위치보다 더 오른쪽에 나타나게 된다.

Fig. 6.

(Color available online) Correlation results for a superimposed LFM signal in Doppler environment.

두 첨두치는 모두 도플러 천이 주파수로 인하여 올바른 위치에 나타나지 않지만 두 첨두치 위치에 대한 중점값은 거리-도플러 커플링 효과에 의한 오차가 상쇄된 위치가 된다. 즉, 두 첨두치의 위치를 평균하면, 도플러 효과로 인한 오차가 없는 도달 시간 값을 얻을 수 있다. 이러한 관계는 다음의 식으로부터 확인할 수 있다. 우선 +LFM 신호에서 정합 필터 출력의 최대값이 나타나는 시간을 t+LFM , –LFM 신호에서 정합 필터 출력의 최대값이 나타나는 시간을 t-LFM라고 하고, 하나의 펄스 길이가 상대적으로 짧아 펄스 내에서의 도플러 천이는 거의 일정하다고 하면 이들은 다음과 같이 나타낼 수 있다.

여기서 R은 수신기와 수중 이동체 사이의 거리이며, t0 은 거리-도플러 커플링 효과에 의한 시간 지연으로써 도플러 천이 주파수에 의하여 t0의 부호는 바뀔 수 있다. 위 식들을 더하면 t0는 상쇄되어 결국 거리 R을 추정할 수 있게 되는데 다음과 같이 나타낼 수 있다.

제안한 방법에서 두 신호의 중첩으로 인하여 송신출력이 3 dB 감소하게 되며, 이로 인해 탐지거리가 감소한다. 하지만 제안하는 중첩된 신호를 송신하는 방법을 사용하면 도플러 효과로 인한 신호의 변화와 무관하게 도달 시간을 추정할 수 있다.

IV. 시뮬레이션 및 결과

4.1 시뮬레이션 구성

제한한 방법의 성능을 분석하기 위하여 시뮬레이션을 수행하였다. 이를 위하여 수중 이동체의 궤적을 선형과 비선형 2가지 형태로 구성하였으며, Fig. 7에서 확인할 수 있다.

Fig. 7.

(Color available online) Trajectory for simulation, (a) linear trajectory, (b) non-linear trajectory.

Fig. 7에서 수신기의 좌표는 (0, 500)에 고정되어 있다고 가정하였다. Fig. 7(a)는 송신기가 (-4,000, -1)에서 시작하여 등속(20 m/s)의 직선 궤적으로 이동하는 상황을 가정한다. 또한, Fig. 7(b)는 궤적이 비선형적으로 움직이며, 속도 변화는 Fig. 8과 같이 설계되었다. 이 때, 송신기의 궤적은 Lemniscate 궤적에 따라 조절되며 다음과 같은 식으로 나타내어진다.^[13]

시뮬레이션에서 a = 2,500 m로 설정하였고, fw = 10^-7 Hz로, 그리고 신호 전체 지속시간은 600 s로 설정하였다. 이 경우 최고 속도는 약 25 m/s이며, 평균 속도는 21 m/s로 설정된다. 즉, 송신기는 비선형적인 궤적을 따라 움직이며, 속도도 시간에 따라 변화한다. 이렇게 설계된 궤적과 속도 변화를 가진 환경에서 도달 시간을 계산하기 위해 해당 경로들이 사용되었다.

Fig. 8.

(Color available online) Change of a vehicle velocity in the non-linear case.

4.2 시뮬레이션 결과

앞서 설명한 것과 같은 환경에서 시뮬레이션을 진행하였다. 수중 이동체는 (-4,000, -1)에서 시작하여 Fig. 5와 같은 신호를 주기적으로 송신하며 Pulse Repetition Interval(PRI) 1 s로 하였다. 수중 이동체가 선형적으로 이동하는 경우에는 8,000 m을 이동하며, 수신기에는 전체 구간 길이 8,000 m를 20 m/s의 속도로 이동하였으므로 400개의 펄스가 도달하게 된다. 수신기에 도달된 신호는 +LFM에서 정합 필터 출력의 최대값이 나타나는 시간과 –LFM에서 정합 필터 출력의 최대값이 나타나는 시간을 Eqs. (5)와 (6)을 통하여 구하였다. 즉 거리는 측정된 2개의 첨두치 사이의 중간값에 해당하며, 이를 통해 수중 이동체와 수신기 사이의 거리를 추정한 결과를 Fig. 9에 나타내었다.

Fig. 9.

(Color available online) Ranging results, (a) linear trajectory, (b) non-linear trajectory.

거리 추정의 정확성을 평가하기 위해 추정된 거리와 실제 송신기와 수신기 사이의 거리 차이를 평균 제곱근 오차(Root Mean Squared Error, RMSE)로 계산 하여 Table 1에 나타내었다. 도플러 편이에 의하여 발생되는 오류를 확인하기 위하여 20 m/s 속력으로 이동한 결과와 25 m/s로 이동한 결과에 대하여 분석하였다. 선형 궤적의 예에서 속도가 20 m/s에서의 +LFM과 –LFM 신호의 정합 필터 출력의 첨두치 값을 이용하여 추정했을 때의 평균 제곱근 오차는 각각 22.6 m와 25.8 m로 나타났다. 이에 반해 제안한 방법의 결과는 19.6 m로, 보다 낮은 오차를 보였다. 속도가 25 m/s에서의 LFM과 –LFM 신호의 평균 제곱근 오차는 각각 28.8 m와 32.1 m로 나타났으며, 제안한 방법의 결과는 24.8 m로 더 나은 결과를 보였다. 또한 송신기가 비선형적인 Lemniscate 궤적을 따라 이동하는 상황에서의 결과에서도 거리-도플러 커플링에 의한 영향을 최소화한 신호의 도달 시간이 보다 정확하게 나타나는 것을 확인할 수 있다. 평균 속도 약 20 m/s일 때의 +LFM의 정합 필터 출력의 첨두치 값을 이용하여 추정한 도착 거리의 평균 제곱근 오차 값은 13.7 m이고, –LFM일 때의 값은 11.8 m였다. 평균 속도 약 25 m/s일 때의 +LFM의 도착 거리의 평균 제곱근 오차 값은 16.5 m이고, –LFM일 때의 값은 13.6 m로 나타났다. 하지만 제안한 방법으로 두 첨두치의 평균값을 이용하여 TOA를 추정한 결과의 평균 제곱근 오차는 평균 속도 약 20 m/s일 때의 평균 제곱근 오차 값은 10.5 m, 25 m/s일 때의 평균 제곱근 오차 값은 10.9 m의 결과를 보였다. 이를 통해 제안한 방법이 도달 시간 추정에서 상대적으로 더 정확한 결과를 도출한다는 것을 확인할 수 있다. 또한 +LFM과 –LFM 신호의 결과와 제안한 방법의 상대오차를 구하여 Fig. 10(a)와 (b)에 나타내었다. 이 때 상대오차 Er은 다음과 같이 계산하였다.

여기서 x는 실제 시뮬레이션에서 설정한 TOA 값이며, x^은 추정된 TOA 값이다. 추정된 TOA 값과 실제 TOA 값 사이 차이의 절대값을 실제 TOA 값으로 나누어 상대 오차를 구하였다.

Fig. 10.

(Color available online) Relative error at v = 20 m/s(a) linear trajectory, (b) non-linear trajectory.

V. 결 론

본 논문에서는 수중 이동체의 시험평가 과정으로의 적용을 위하여 동기화된 송신기가 장착된 수중이동체와 수신기 사이의 거리 추정의 정확성을 향상시키기 위한 중첩된 LFM 신호를 제안하였다. 제안한 방법은 +LFM 신호와 –LFM 신호를 중첩시켜 구성하고, 두 신호의 정합 필터 출력의 첨두치 값을 이용하여 도달 시간을 추정한다. 즉, 서로 직교성을 갖는 2개의 LFM 신호를 사용함으로써 거리-도플러 커플링 효과에 의한 오차를 보정하였다.

제안한 방법은 2종류의 신호를 중첩하였기에 송신 전력은 3 dB 감소하지만 보다 정확한 거리 추정을 위해 추가적인 도플러 천이 주파수 추정이 필요하지 않다. 시뮬레이션을 통해 수중 이동체의 선형 및 비선형 이동 궤적에서의 거리 추정 성능을 비교 분석하였으며, 그 결과 제안한 방법은 +LFM 또는 –LFM 신호만을 사용한 경우보다 평균 제곱근 오차가 감소하는 것을 확인하였다.

향후 알고리즘의 성능을 더욱 개선하고 다중경로효과 등 여러 간섭이 있는 환경에서의 시뮬레이션과 실험을 통해 실제 환경에서의 적용 가능성을 검토하는 추가 연구가 필요하다.