I. 서 론
수중감시시스템은 수상 혹은 수중의 음향표적을 탐지하여 추적하는 시스템이다. 수중의 경우 해양 매질의 특성으로 인하여 전자파의 손실이 큼에 따라 사용이 불가피 하며, 손실이 적은 음파를 사용한 소나의 기술이 활용된다.[1], [2]
수중감시시스템의 탐지기술은 음파 송신 후 표적에 반사된 신호를 수신하여 정보를 얻는 능동소나와 표적에서 방사되는 소리를 수신하여 정보를 얻는 수동소나로 분류된다. 수동측거소나(Passive Ranging Sonar, PRS)는 수동소나의 한 종류로서 표적을 탐지하고, 표적의 방위와 거리를 산출하는 특성을 갖는다.
수동측거 기술은 최소 3개 수신기 배열을 필요로 하며, 표적으로부터 방사된 음파면의 곡률로 인한 수신기 간의 도달시간 차를 이용한 시간지연 기법과 2개의 방위선을 이용한 삼각측량기법이 사용된다.[3], [4] 이러한 기술에는 수신기의 정확한 위치정보가 요구되며, 수신기의 부정확한 위치정보가 발생할 경우 방위와 거리 정확도 성능이 저하되는 한계가 있다.[5]
설계된 수신기의 배열은 함정에 설치 시 또는 운용 환경에서 함의 외형적 형상 변화 등 기타 여건으로 인하여 위치오차가 발생할 수 있다.이는 방위와 거리 정확도 성능 저하에 영향을 주므로 수신기 배열의 위치오차를 추정하고 보상할 필요가 있다. 본 논문에서는 수신기 배열의 위치오차를 추정하기 위하여 최적화 탐색 기법인 유전자 알고리즘을 사용하며, 산출된 위치오차 값을 이용하여 수신기 배열간의 시간지연 값을 보상하여 거리 정확도 성능이 개선됨을 보이고자 한다.
제 1장에서는 PRS의 기술동향과 연구 필요성을 언급하였으며, 제 2장에서는 PRS의 측거 기술과 수신기 배열의 위치 오차에 따른 거리 정확도 성능에 대한 영향성을 언급하고자 한다. 또 제 3장에서는 유전자 알고리즘 기반의 수신기배열 위치오차 추정기술 소개 및 해상데이터를 통한 실험적 검증을 보이고자 한다. 마지막으로 제 4장에서는 연구에 대한 결론을 맺는다.
II. 측거 기술
2.1 PRS의 측거 기술
PRS는 잠수함 플랫폼의 좌/우현에 각각 3개의 부배열로 구성되었으며, 함에 설치된 부배열 위치에 따라 함수(FWD), 중앙(MID), 함미(AFT)로 분류된다. 부배열은 제 1장에서 언급한 수신기 배열과 같은 개념으로 정의한다.
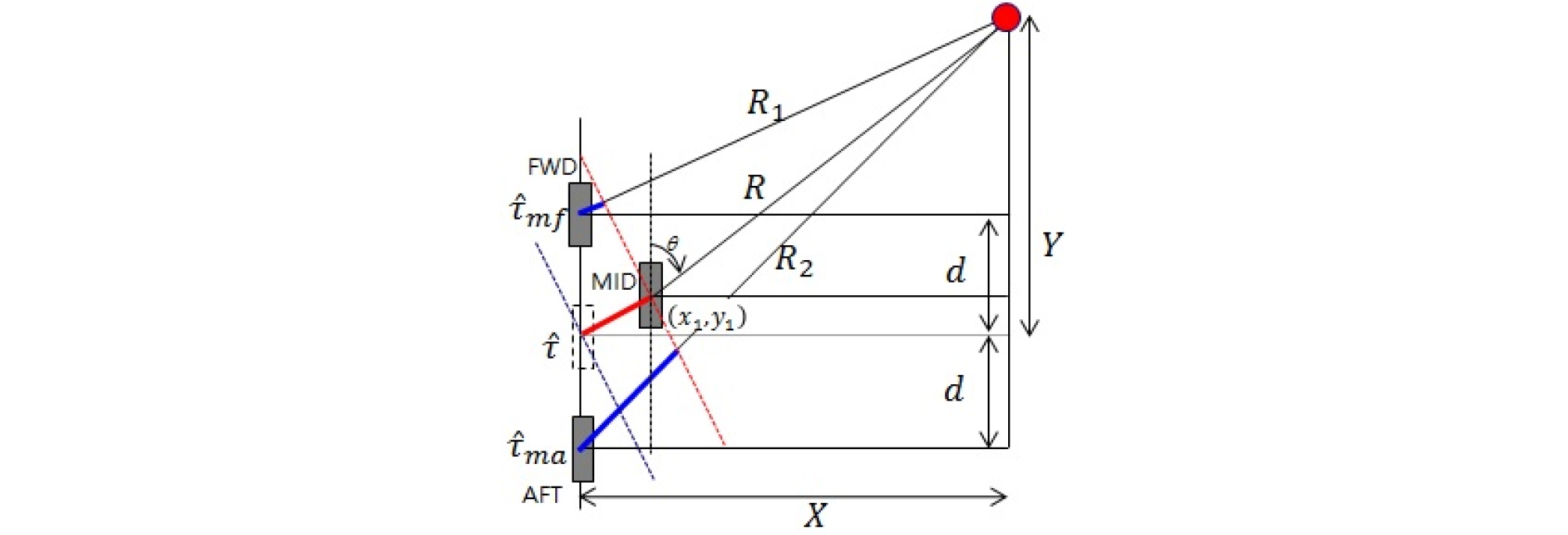
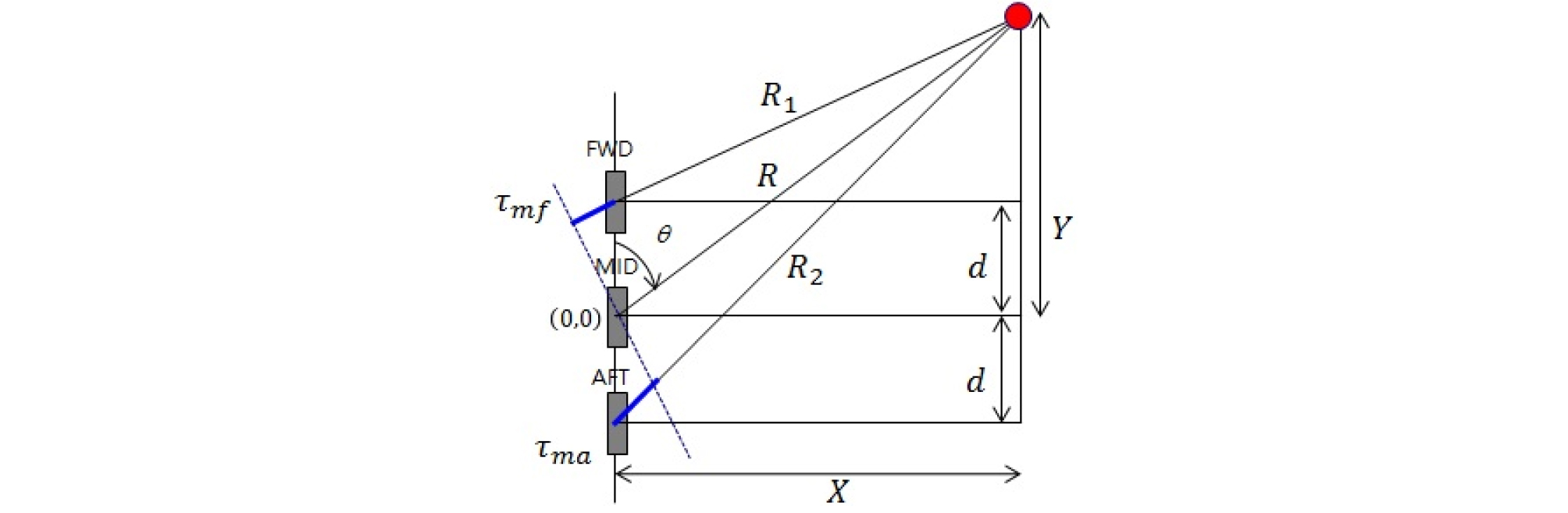
잠수함 플랫폼의 측면에 설치된 3개의 부배열은 일직선상에 균등한 간격으로 구성되었으며, Fig. 1.과 같다. 부배열의 위치정보는 중앙 부배열을 기준으로 부배열 간격 값을 통하여 위치정보를 얻을 수 있다.
표적으로부터 방사된 음파를 수신할 때 물리적인 부배열 위치로 인하여 시간지연이 발생된다.[6] 방위와 거리 산출에 사용되는 시간지연은 중앙 부배열을 기준으로 중앙-함수 시간지연과 중앙-함미 시간지연이 된다. 시간지연과 삼각측량기법을 이용한 방위와 거리 관계식은 다음과 같다.
| $$\theta=cos^{-1}(\frac{c(\tau_{mf}-\tau_{ma})}{2d}).$$ | (1) |
| $$R=\frac{d^2\sin^2(\theta)}{c\vert\tau_{mf}+\tau_{ma}\vert},$$ | (2) |
여기서 는 부배열 간격이고 는 음속, 는 중앙-함수 부배열 간의 시간지연, 는 중앙-함미 부배열 간의 시간지연을 뜻한다.
방위는 두 개 벡터의 사이 각을 도출하는 개념으로 중앙-함수 시간지연과 중앙-함미 시간지연을 각각 이용하여 두 개의 방위 산출이 가능하다. Eq. (1)에서는 중앙-함수 시간지연과 중앙-함미 시간지연의 평균값을 이용하여 하나의 방위를 산출한다. 반면, 거리는 두 개의 방위선을 이용하여 표적의 거리를 도출하는 개념으로 Eq. (2)가 사용된다.
방위와 거리 관계식은 부배열의 위치정보인 부배열 간격 인자를 사용하게 된다. 따라서 실제 설치된 함에서의 부배열 위치정보가 상이할 경우 정확도 성능이 저하된다.[4]
부배열의 위치오차 형상은 대표적으로 Fig. 2와 같다. Fig. 2의 (a)는 부배열 축이 회전된 것으로 부배열 간격은 균등한 선형 상태를 유지한다. 반면, (b)와 (c)는 비선형 상에 3개의 부배열이 놓여있으며 (b)는 전체 배열 길이에 변화가 없고, (c)는 전체 배열 길이가 변화된 형상이다. (a)의 경우 축이 회전되었으나 선형 상에 부배열이 존재함에 따라 전체 부배열 길이 증감에 영향 없이 거리보다 방위 정확도에 영향을 미친다. (b)와 (c)는 비선형으로 구성되어 방위보다 거리 정확도에 영향을 미치며, 전체 배열 길이에 따른 영향도 존재한다.[4], [5]
임의로 표적을 진북기준 방위 60도, 거리 9144 m, 음속 1500 m/s로 모의하여 부배열 형상에 따른 오차 영향성을 분석하였다. 중앙 부배열을 기준으로 부배열 간의 시간지연을 산출하였으며 Eqs. (1)과 (2)를 이용해서 방위와 거리를 산출하였다. 산출된 방위와 거리는 Table 1과 같다.
Table 1. Analysis of bearing and distance according to the type of position uncertainty.
| (a) | (b) | (c) | |
| Bearing / Difference (unit :degree) | 65.0 / 5.0 | 60.0 / 0.0 | 59.9 / 0.1 |
| Range / Difference (unit :m) | 9227.0 / 83.2 | 7604.2 / 1539.8 | 5439.8 / 3704.2 |
3개의 부배열이 동일한 직선상에 존재하며 축만 회전된 (a)의 경우에는 거리보다 방위 정확도에 민감함을 알 수 있다. 반면, 비선형상 (b)와 (c)는 방위보다 거리 정확도에 영향을 줌을 알 수 있다. 또한 전체 배열 길이에 대한 거리 오차 영향성이 나타나며, 이는 전체 배열 길이 증감에 따른 영향성 분석이 필요해 보인다.
본 논문에서는 거리정확도에 영향을 주는 비선형 형상에 대하여 연구하였으며, 전체 배열 길이의 영향성을 배제한 Fig. 2(b)를 고려하여 진행하였다.
방위와 거리 산출에 중요한 요소인 시간지연의 산출은 중앙 부배열을 기준으로 수행되므로, 기준점인 중앙 부배열의 위치오차를 추정하고자 한다. 중앙 부배열 위치오차로 인한 시간지연 오차 개념도는 Fig. 3과 같다.
시간지연 값은 중앙 부배열의 수신신호를 기준으로 함수와 함미 부배열에 수신된 신호의 상호상관을 통하여 산출된다. 이에 본 논문에서는 상대적인 중앙 부배열의 위치오차만을 고려하며 중앙 부배열의 위치오차에 대한 시간지연 보상 값은 아래와 같다.
| $$\widehat\tau=\frac{x_1\sin(\theta)+y_1\cos(\theta)}c,$$ | (3) |
여기서 와 은 중앙 부배열 위치오차를 뜻한다. 기준점으로부터 벗어난 벡터를 통하여 시간지연 오차 값이 산출되며, 중앙 부배열 위치오차에 따른 시간지연 보상 식은 아래와 같다.
| $$\tau _{mf} = {\hat{\tau}} _{mf} - {\hat{\tau }}.$$ | (4) |
| $$\tau _{ma} = {\hat{\tau }} _{ma} - {\hat{\tau }}.$$ | (5) |
중앙 부배열 위치오차에 대한 시간지연 오차를 보상함에 따라 중앙 부배열의 위치가 기준점에 놓여진 Fig. 2 개념과 동일하게 중앙-함수 시간지연과 중앙-함미 시간지연이 산출된다. 따라서 기존 방위와 거리 산출식의 사용이 가능하다.
III. 유전자 알고리즘
PRS 거리정확도 성능은 부배열의 위치오차와 밀접한 관계를 갖는다. 이에 본 장에서는 유전자 알고리즘을 통하여 PRS 부배열의 위치오차를 추정하고 PRS 거리정확도 성능이 개선됨을 보이고자 한다.
본 논문에서는 거리정확도의 성능이 개선됨을 확인하기 위하여 부배열 위치오차 보상 전/후의 거리오차율을 산출하여 비교하고자 한다. 보상 전 거리오차율은 위성항법장치(Global Positioning System, GPS)를 통해 측정된 표적과의 거리(GPS 거리정보)와 PRS를 통해 측정된 표적과의 거리(PRS 거리정보)를 비교한 것이다. 보상 후 거리오차율은 GPS 거리정보를 바탕으로 중앙 부배열 위치오차 값을 적용하여 재 산출된 거리와 PRS 거리정보와의 거리를 비교한 것이다. 이는 유전자 알고리즘을 통해 선택된 부배열의 위치오차 값을 GPS 거리정보에 적용하여 기존 PRS 거리정보와 유사한지 탐색하는 역산기법이다.
3.1 유전자 알고리즘 기반의 위치오차 추정
유전자 알고리즘은 생물학적 진화 과정에 기초하 여 최적화 탐색 기법으로 널리 사용된다. 유전자 알 고리즘의 특징으로는 진화 과정이 수행될 때마다 적 합성 판별을 수행하여 우수한 유전자를 생존, 증식 함에 따라 최적화된 해를 도출하는 것에 있다. [7], [8]
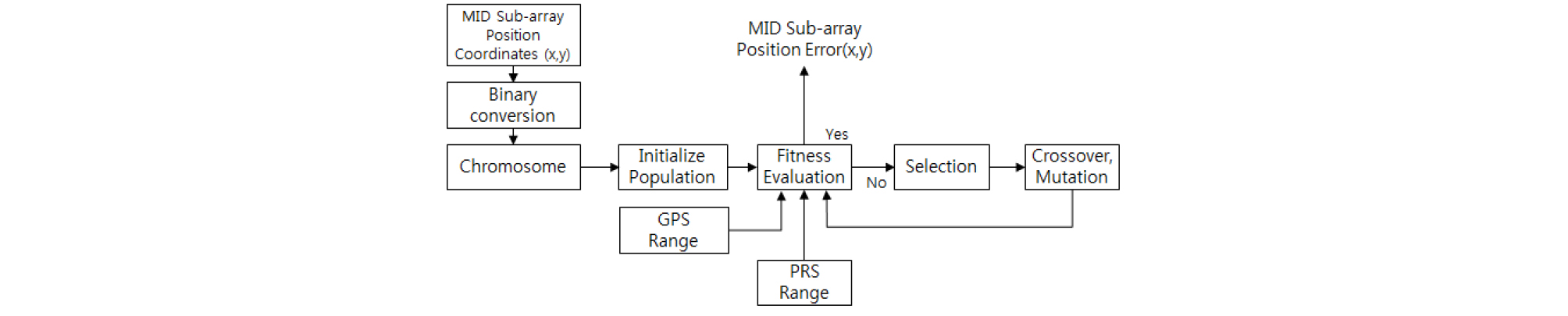
본 논문에서 제시하는 유전자 알고리즘의 구조도는 Fig. 4와 같다.
기준점이 되는 중앙 부배열의 위치좌표는 (0, 0)으로 설정하고, 부배열 간격 정보를 이용하여 함수와 함미의 위치좌표도 결정한다. 앞서 언급한 바와 같이 본 논문에서는 Fig. 2(b)와 같은 형상을 추정함에 따라 중앙 부배열의 위치오차만을 고려한다. 중앙 부배열의 위치좌표 를 각각 이진수로 변환하고 유전자형을 결정한다.
초기 유전자 결정 단계에서는 결정된 유전자형과 같은 형태로 임의의 후보군의 유전자를 생성하고 결정하는 것으로 최초 1회만 수행된다. 본 단계에서는 중앙 부배열 위치좌표를 중점으로 바둑판 모양으로 유전자 후보군을 배치하였다. 이는 유전자 알고리즘의 특성인 모집단 상호작용을 고려한 것으로 특정 위치에 유전자 후보군이 밀집되어 지역 최적화에 빠지는 위험을 방지하기 위함이다.[7], [8]
결정된 초기 유전자들은 적합성 판별 단계를 거쳐 우수한 유전자가 선정되며, 이를 바탕으로 유전자 간의 교배와 돌연변이가 수행되어 유전자 증식, 도태로 차세대를 생성한다. 차세대 유전자들은 다시 적합성 판별 단계로 돌아가 반복 수행된다.
유전자 알고리즘은 우수한 유전자만을 활용하는 것이 특징으로 적합성 판별 단계가 중요하다. 본 알고리즘에서는 유전자 알고리즘을 통해 선택된 중앙 부배열 위치오차 후보군을 GPS 거리정보에 적용하여 재 산출된 거리정보와 기존 함정에 설치된 PRS 거리정보의 오차율이 0 %인가로 적합성 판별을 수행한다. 이는 PRS 중앙 부배열의 위치를 변경해가며 재 산출된 거리정보가 기존 PRS 거리정보와 일치하는지 탐색하는 과정으로 함에 설치된 PRS 부배열 형상을 추정하는 것과 동일한 개념이다.
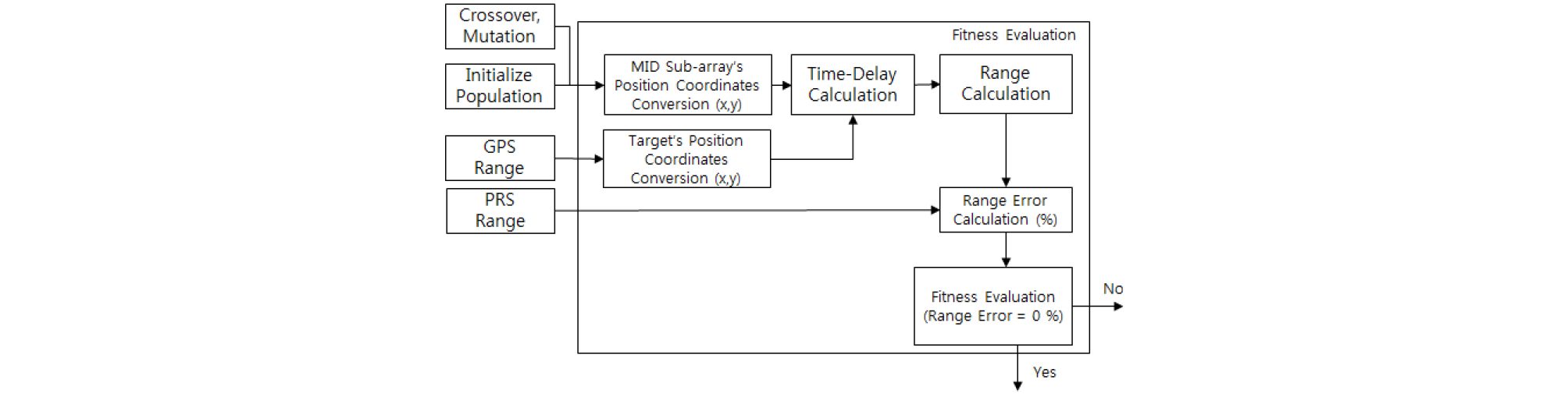
적합성 판별 단계의 상세 구조도는 Fig. 5와 같다.
최초 1회는 초기유전자가 입력되며 이후에는 도태, 증식 단계에서 결정된 차세대 유전자가 입력된다. 입력된 유전자는 중앙 부배열의 위치좌표 로 재 변환되어 임의의 PRS 부배열 형상이 결정된다. 또한 GPS를 통해 획득된 거리정보는 기준점(0, 0)과 표적간의 거리로 간주하여 표적의 위치좌표 값으로 역산하여 사용한다. GPS 거리정보를 이용하여 표적의 위치좌표를 산출하는 것은 PRS 신호처리 과정에서 발생하는 거리오차요소를 배제하기 위함이다.
임의로 추정된 PRS 부배열의 위치좌표와 표적의 위치좌표를 이용하여 부배열 간의 시간지연을 산출하고, 이를 Eq. (2)에 대입하여 거리를 재 산출한다. 재 산출된 거리는 기존 PRS 거리정보와 비교하여 거리오차율이 산출되며 관계식은 다음과 같다.
| $$R_{err}(\%)=\sqrt{\frac1N\sum_{n=1}^N(\frac{R(n)-\widehat R(n)}{R_{upper}})^2}\times100\%,$$ | (6) |
여기서 은 PRS를 통하여 측정된 거리이며 은 유전자 알고리즘을 통해 재 산출된 거리, 는 측정된 거리의 상한 값, 은 측정된 샘플수를 뜻한다.
거리오차율이 0 %인 경우 적합성 판별에 만족하여 유전자 알고리즘은 종료되고 중앙 부배열 위치오차 값이 출력된다. 반면 적합성 판별에 만족하지 않은 경우 거리오차율이 낮은 순으로 정렬하여 우수한 유전자가 결정되며 유전자 알고리즘이 반복 수행된다. 특정 세대수가 생성된 이후에는 거리오차율이 가장 낮은 중앙 부배열의 위치오차 값을 출력하여 최적의 해를 도출한다.
3.2 해상데이터를 통한 실험적 검증
본 절에서는 해상데이터를 이용하여 제시한 알고리즘에 대한 실험적 검증을 하고자 한다. PRS와 표적 간의 시험 거리는 1828.8 m ~ 7315.2 m이며 약 50 min간의 GPS와 PRS 거리정보를 수집하였다.
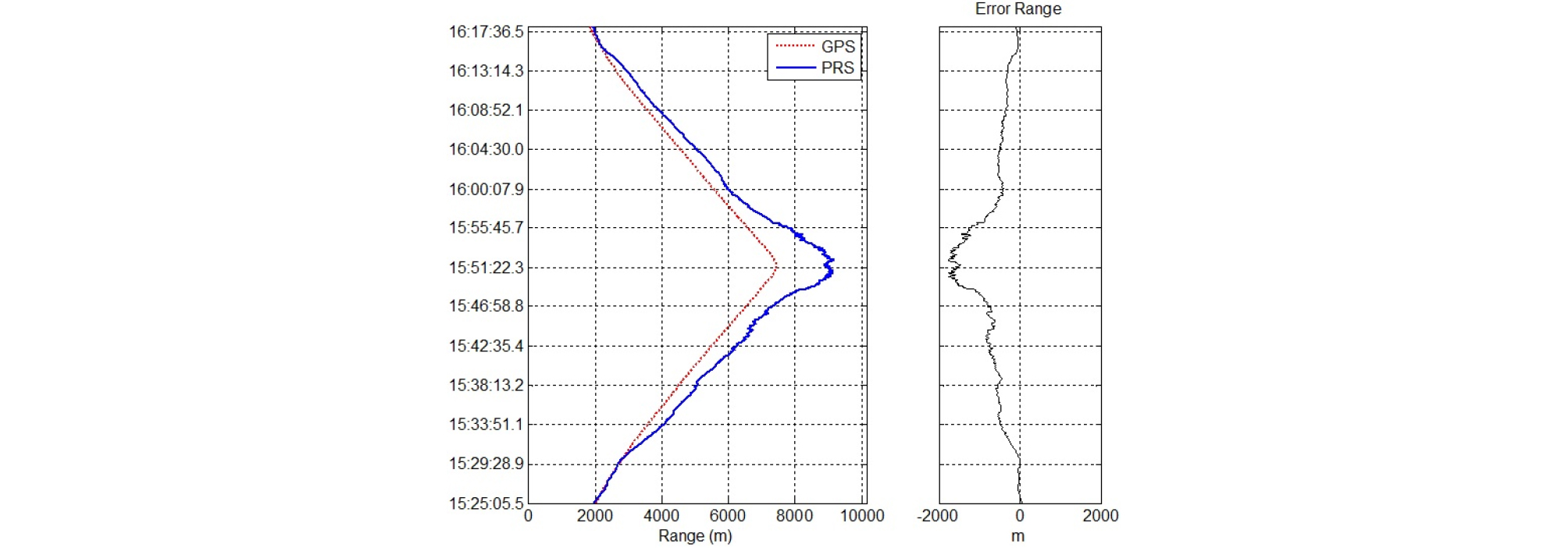
GPS 거리정보와 부배열 위치오차 보상 전의 PRS 거리정보는 Fig. 6과 같다. PRS 거리정보는 일직선상에 3개의 부배열이 존재하며 동일한 간격으로 배치되었다고 가정하였으며 위치오차에 대한 보상 전의 Eq. (2)를 근거로 산출된 값이다. GPS와 PRS 거리의 오차율은 약 9.8 %로 나타나며 최대오차 거리는 약 1772.3. m로 분석되었다.
거리 오차율을 감소시켜 거리정확도 성능을 개선하고자 본 논문에서 제시한 유전자 알고리즘 기반의 부배열 위치오차를 추정하였다.
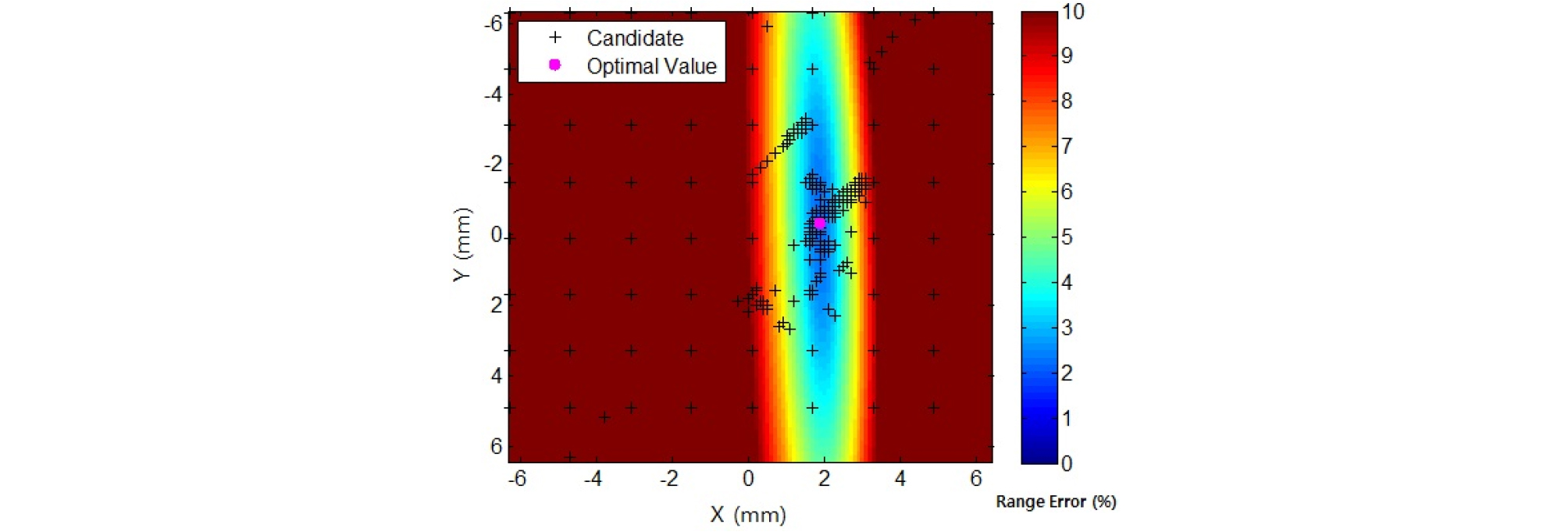
Fig. 7은 이해를 돕기 위해 기준점 (0,0)에 설계된 중앙 부배열을 위치오차를 x, y 축으로 ± 6 mm로 고려하여 전역조사를 수행한 거리오차율 결과를 배경으로 유전자 알고리즘에서 추출된 우수한 유전자의 위치좌표를 중첩하여 표현하였다.
GPS 거리정보를 역산하여 부배열의 위치좌표를 산출하고, 바둑판 형태의 초기 유전자를 바탕으로 유전자 알고리즘을 수행하였다. 적합성 판별에서 선정된 유전자를 후보군(+)으로 표기하였으며, 100세대가 생성 될 때 까지 반복 수행하였다. 유전자 알고리즘이 종료된 후 최적의 유전자(●)로 선정된 중앙 부배열의 위치정보는 x축 1.9 mm, y축 –0.3 mm이다.
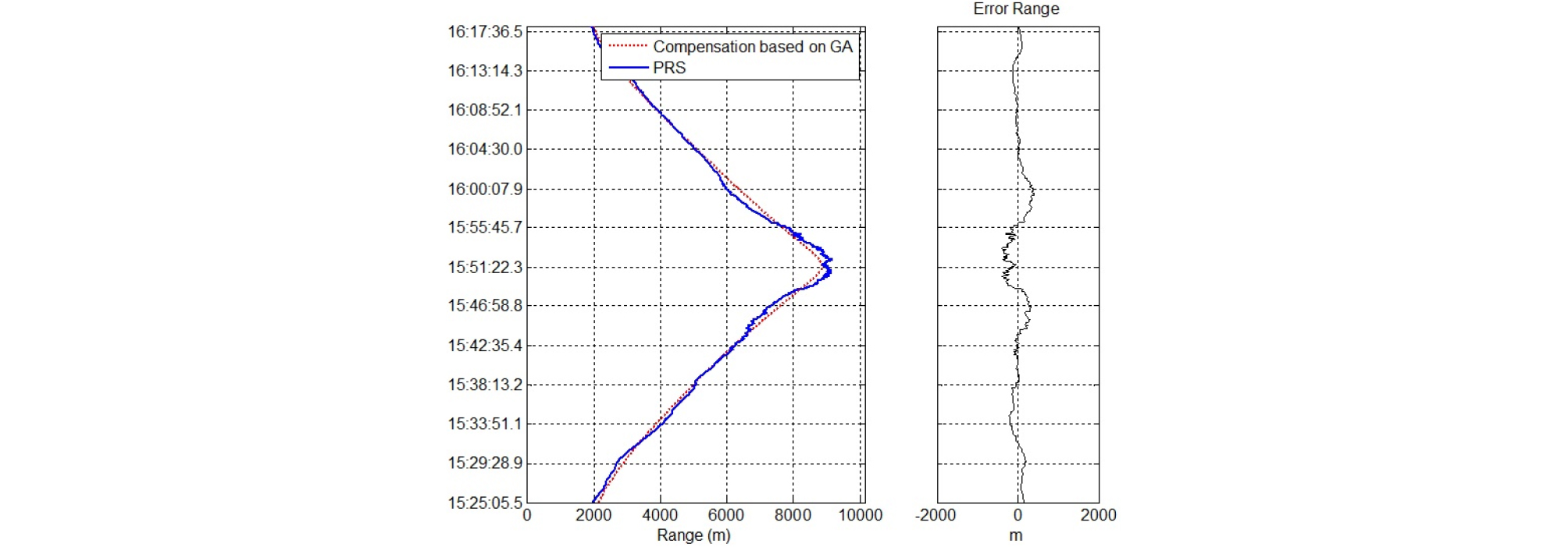
추정된 중앙 부배열 위치정보를 근거로 시간지연 보상 값을 Eq. (3)을 통하여 산출하고, Eqs. (4)와 (5)를 근거로 보상하였다. 이후에 기존 거리산출 식인 Eq. (2)를 통하여 거리를 재산출하였으며, 재 산출된 거리와 보상 전의 PRS 거리정보는 Fig. 8과 같다.
유전자 알고리즘을 기반으로 부배열 위치오차를 추정하고 보상된 거리정보와 PRS 거리정보의 거리오차율은 약 2.2 %이며, 최대오차 거리는 약 406.6 m로 분석되며 거리오차율이 감소되었다.
IV. 결 론
PRS는 3개의 부배열로 구성되었으며 부배열 간의 시간지연과 삼각측량기법을 이용하여 방위와 거리를 산출하는 특징을 갖는다. 이러한 측거 기술은 부배열의 위치정보가 부정확할 경우 방위와 거리 정확도의 성능이 저하되는 한계가 있다. 이를 개선하기 위하여 본 논문에서는 부배열의 위치오차 추정 및 보상에 대한 연구 필요성을 언급하였다.
본 논문에서는 최적화 탐색기법인 유전자 알고리즘을 기반으로 PRS의 중앙 부배열 위치오차 추정 및 보상 방법을 소개하였으며, 해상데이터를 이용하여 실험적 검증을 수행하였다. 또한 GPS 거리정보를 역산하여 표적과 부배열의 위치좌표를 결정하고, 중앙 부배열의 위치오차에 대한 후보군을 생성하였다. 후보군을 바탕으로 중앙 부배열 위치오차를 보상하여 재 산출된 거리는 PRS 거리정보와 비교하였으며, 거리오차율이 낮은 후보군을 탐색하여 위치오차를 추정하는 역산 기법으로 접근하였다. 이는 PRS 거리 산출 시 사용되는 신호처리 알고리즘에서 거리 오차의 요소들을 배제하고 부배열의 위치오차만을 고려하기 위함이다.
해상에서 획득한 GPS 거리정보와 PRS 거리정보의 거리오차율은 부배열 위치오차를 보상하기 전에 약 9.8 %로 나타났다. 유전자 알고리즘 기반으로 기준점이 되는 중앙 부배열의 위치오차를 추정한 결과 x축 1.9 mm, y축 –0.3 mm로 분석되었다. 추정된 중앙 부배열 위치오차를 보상하여 재 산출된 거리정보와 PRS 거리정보의 거리오차율은 약 2.2 %로 분석되었다. 이는 부배열 위치오차를 보상하기 전과 비교하여 약 4.5배 거리오차율이 감소됨을 알 수 있다.



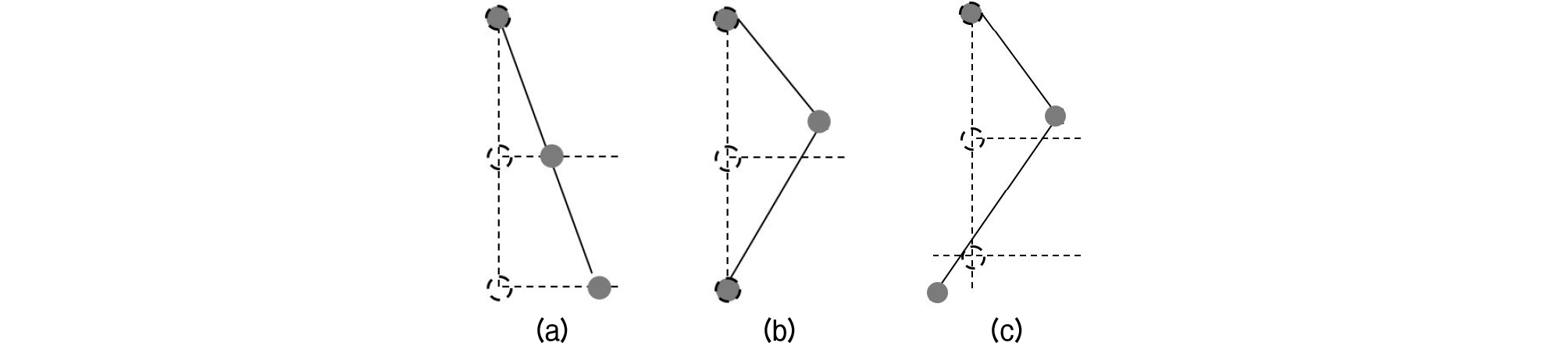
 : true position,
: true position,  : assumed position).
: assumed position).