I. 서 론

천해에서 해양환경의 시변동성에 의해 발생되는 해수면 거칠기는 음파의 산란을 발생시킨다. 해수면 거칠기가 증가할수록 해수면 경로에서 산란되어 수신되는 음파들의 지연시간과 에너지 차이가 증가하여 더 큰 도플러 확산이 발생한다.^[1] 또한 해수면 거칠기에 의해 발생하는 음파 산란은 주파수가 증가할수록 해수면 산란의 영향이 증가한다.^[2,3] 수중음향 통신채널에서 해수면 거칠기에 의한 도플러 확산은 채널의 상관시간(Tc)을 감소시키고, 고속 페이딩 채널을 야기하여 통신성능을 악화시킨다.^[4,5] 통신 대역폭 확보를 위하여 고주파수 반송 주파수를 사용할수록 채널의 시변동성이 증가하며, 통신신호 복조 과정에서 짧은 상관시간으로 인하여 주기적인 채널 업데이트가 필요하게 되어 신호처리 과정에서 낮은 효율을 보인다. 임의의 해역에서 해수면 거칠기에 따른 채널의 시변특성을 파악 할 수 있다면, 사전에 통신신호의 길이를 조절할 수 있기 때문에 신호처리 관점에서 효율적으로 통신신호를 설계할 수 있다. 이러한 이유로 해수면 거칠기에 따른 해수면 경로의 시변 특성을 분석하는 연구가 중요하다. 해수면 거칠기에 따른 채널의 시변동성 특성을 분석하고 시변 채널 모델을 개발하기 위한 연구가 수행되어 왔다.^[6,7,8,9] Qarabaqi와 Stojanovic^[6]은 시변 환경을 대규모 변동성과 소규모 변동성으로 구분하여 이에 따른 통계적 특성 분석 연구를 수행하였으며, Siderius와 Porter^[7]은 시간에 따른 해수면 변동과 송수신기 이동에 의해 발생하는 도플러 효과를 반영한 채널 모델인 VirTEX를 개발하였다. 위의 시변 채널 모의 연구들은 수면 거칠기 변화에 따라 발생하는 채널의 통계적 특성이 반영되지 못한 한계점을 가진다.

본 논문에서는 해양에서 발생될 수 있는 수면 거칠기와 채널 시변 파라미터의 통계적 특성과의 상관관계 분석을 위하여 수조 실험을 수행하였다. 수조실험은 해양에서 발생되는 해수면 거칠기와 발생 기작 차이가 존재하지만, 외부 환경조건을 제어하면서 수면 거칠기를 발생하는 등 통제 가능한 환경에서 음향실험을 할 수 있다는 장점이 있다. 수면 거칠기는 레일리 파라미터로 변환하여 사용하였으며, 수면 경로의 시변 채널 파라미터는 통신신호의 반송 주파수와 대역폭에 의한 주파수 의존성을 반영한 가중 유효 도플러 확산[Weighted Root Mean Square(RMS) Doppler spread, wσν]과 상관시간(Tc)을 이용하여 분석하였다.

II. 이 론

2.1 수면 경로의 시변 채널특성 추출

수면 거칠기와 시변 채널특성의 상관관계를 파악하기 위해 유효 도플러 확산과 상관시간을 시변 채널 파라미터로 사용하여 분석하였다. 유효 도플러 확산은 추정된 채널의 도플러 효과를 나타내는 산란 함수[Scattering function, P(τ,v)]로부터 계산이 가능하다. 여기서 𝜏는 지연시간, 𝜐는 주파수 천이를 나타낸다. 산란함수는 Eq. (1)과 같이 확산함수[Spreading function, S(v,τ)]의 기댓값(E[])으로 표현된다.^[10]

확산함수는 시변 채널 임펄스 응답(h(τ,t))의 푸리에 변환이며, Eq. (2)와 같이 표현 가능하다.^[10]

본 논문에서 h(τ,t)는 최소 자승법(Least square)을 사용하여 추정된 통신신호의 기저대역(Baseband) 시변 채널 임펄스 응답을 사용하였다.^[11] 산란 함수를 지연시간(𝜏)에 대하여 적분하면 주파수 천이에 따른 에너지 변화를 나타내는 도플러 전력 스펙트럼[Doppler power spectrum, Pd(v)]을 도출할 수 있다.

유효 도플러 확산은 도플러 전력 스펙트럼의 에너지(Pd(νk))와 도플러 천이(νk)의 함수로 Eq. (4)와 같이 표현 가능하다.^[12]

본 논문에서는 수면 경로의 시변 채널특성을 분석 및 비교하기 위하여 전체 다중경로 중 수면 경로에 해당하는 값을 이용하였고, 수면 거칠기에 의해 발생하는 도플러 전력 스펙트럼 에너지의 차이를 충분히 반영할 수 있도록 –40 dB의 경계값(Threshold)을 선정하여 유효 도플러 확산을 계산하였다.

시변 채널에서 시간에 따른 채널 유사성을 평가하기 위하여 채널이 일정하게 유지되는 시간인 상관시간을 사용하였다.^[13,14] 본 연구에서는 추정된 수면 경로 에너지의 자기상관함수를 이용하여 상관도 값이 0.8 이하로 감소하지 않는 시간을 상관시간으로 정의하고 분석에 사용하였다.

2.2 실효치 파고를 이용한 레일리 파라미터 변환

수조에서 측정된 파고 데이터를 파워 스펙트럼 밀도 분석을 통해, 수면 스펙트럼(S(f))을 도출하였다. 수면 스펙트럼을 주파수에 대하여 적분하여 수면 스펙트럼의 0차 모멘트(m0)를 계산하였다[Eq. (5)]. Eq. (6)를 이용하여 0차 모멘트로부터 0차 모멘트 파고(Hm0)를 계산하고, Eq. (7)를 이용하여 실효치 파고(RMS wave height, h)를 계산하였다.^[15,16]

레일리 파라미터는 실효치 파고와 음향학적 파수(Acoustic wavenumber, k)의 관계를 나타내는 파라미터로써, 본 연구에서는 측정된 수면 거칠기에 대한 지표로 사용하였다.^[17,18] 레일리 파라미터(𝜒)는 Eq. (8)로 표현할 수 있다.

여기서 k는 음향학적 파수이며 [, f는 중심 주파수, c는 음속임], h는 실효치 파고, θi는 입사각이다. 일정한 주파수, 음속을 가지는 경우 레일리 파라미터는 수면 거칠기에 의한 함수로 표현 가능하다. 레일리 파라미터가 작을수록 수면 거칠기의 변화가 긴 주기를 갖는 큰 거칠기 특성을 보이며, 레일리 파라미터가 커질수록 수면 거칠기의 변화 짧은 주기를 갖는 작은 거칠기 특성을 보인다(Fig. 1).^[17]

Fig. 1.

(Color available online) Sea surface roughness characteristic by Rayleigh parameter. (a) Small Rayleigh parameter, (b) Large Rayleigh parameter.

본 논문에서는 인위적으로 발생시킨 수면 거칠기를 정량적으로 측정 후 실효치 파고를 계산하였으며, 실험에 사용된 주파수와 수조환경 내부의 일정한 음속을 이용하여 음향학적 파수를 계산하고 송수신기의 수심에 따른 반사각을 이용하여 레일리 파라미터를 도출하였다.

III. 수조실험 및 환경

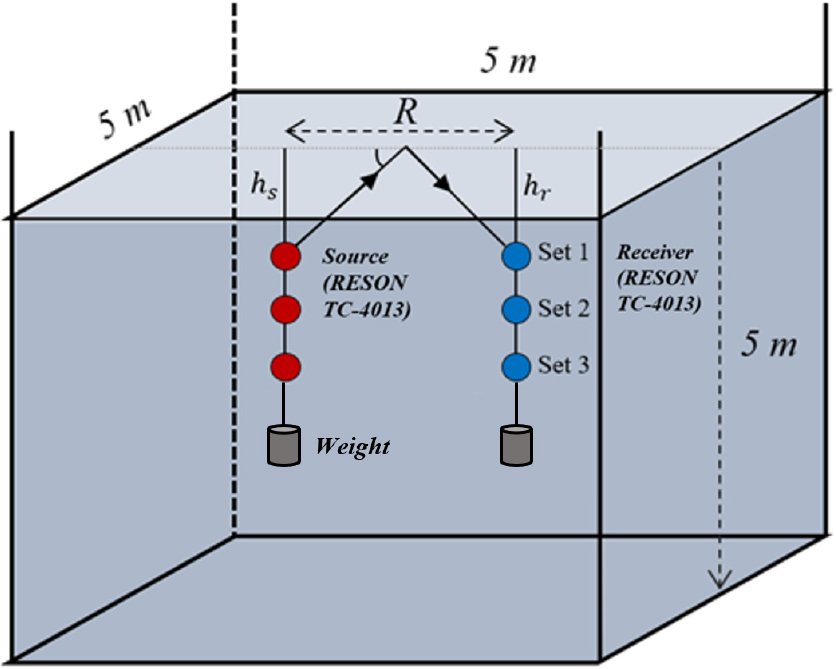
수면 거칠기에 의한 수면 경로 채널 파라미터의 통계적 특성을 비교하기 위하여 한양대학교 내 5 × 5 × 5 m³ 크기의 수조에서 실험을 수행하였다(Fig. 2). 송․수신기는 무지향성 센서(TC-4013, RESON)을 사용하였으며, Conductivity Temperature Density(CTD)를 이용하여 측정한 음속은 1,480 m/s로 모든 수심에서 일정하였다. 송․수신기는 수면 경로가 직접경로를 비롯한 벽, 바닥 경계면 반사파와 분리되도록 위치하였다. 송신기의 수심(hs)과 수신기의 수심(hr)이 동일하도록 설정하여 3개의 수심(Set1: 0.6 m, Set2: 0.7 m, Set3: 1.0 m)에서 실험을 수행하였고, 수면 경로의 수평입사각은 각각 30°, 35°, 40°이었다. 송․수신기 거리(R)는 2 m로 모든 Set에서 동일하였다. 송․수신기 하단에 10 kg의 무게추를 설치하여 송수신기 움직임에 의한 영향을 최소화 시킨 후 도플러 확산에 대해서만 분석을 수행하였다. 실험 간 수면 거칠기는 인위적으로 발생시켜 시간에 따라 거칠기는 감소하였으며, 용량식 파고계[DWG-1000L, ㈜이엔씨시스템]를 사용하여 수면 움직임을 정량적으로 측정하였다.

Fig. 2.

(Color available online) Experimental configuration (Set 1 : hs, hr = 0.6 m, Set 2 : hs, hr = 0.7 m, Set 3 : hs, hr = 1.0 m).

본 논문에서는 고주파수에서 수면 거칠기에 따른 음파 산란과 시변 채널 파라미터의 차이를 비교하기 위하여 128 kHz의 중심주파수를 사용하였으며, 대역폭에 의한 시변 채널 파라미터의 변화를 확인하기 위하여 3가지 대역폭의 통신신호를 설계하였다(Table 1).

통신신호는 탐침신호(Probe signal)와 통신 시퀀스(Communication sequence)로 구성하였다. 탐침신호는 신호 길이 0.05 s의 선형 주파수 변조 신호(Linear Frequency Modulation, LFM) 신호로 통신 시퀀스의 대역폭과 동일한 주파수 범위로 설정하였고, 탐침신호의 정합필터링결과를 이용하여 통신시퀀스의 시작 위치를 동기화하였다. 통신시퀀스는 정보전달을 위한 3.6 s의 정보 시퀀스(Information sequence)와 잔여 인접 심볼 간 간섭(Inter-Symbol Interference, ISI) 제거와 기저대역 채널 추정을 위한 0.4 s의 훈련 시퀀스(Training sequence)로 구성되었다(Fig. 3).

Fig. 3.

(Color available online) Communication signal frame in one bandwidth.

실험이 수행되기 전 4개의 용량식 파고계를 수조의 다른 위치에 설치하여 각 위치에서 수면 거칠기에 따른 해수면 스펙트럼 에너지 변화가 유사한 것을 확인하였다. 실험은 인위적으로 수면 거칠기를 발생 시킨 후 잔잔해질 때까지 약 20 min 동안 40패킷의 송신신호를 송․수신하였으며, 통계 분석에 충분한 데이터를 확보하기 위하여 3회 반복하였다.

해수면 거칠기가 존재하지 않는 Mirror surface에서 추정된 채널을 이용하여 수면 경로가 수신되는 심볼 시간을 추정한 후 수면 거칠기에 따른 시변 채널 파라미터의 통계적 특성을 추출하였다. Fig. 4는 Mirror surface에서 통신신호의 기저대역 채널 추정 결과이다. 추정된 채널은 직접경로가 강하게 수신된 후 수면 경로가 수신되며, 수면 경로 수신 후 수조 벽, 바닥 등에 의한 반사 신호가 수신되었다. 통신신호의 대역폭 증가에 따라 심볼 간격이 감소하여 수면 경로의 에너지가 여러 심볼 시간에 걸쳐 수신되었다. 본 연구에서 수면 경로의 시변 채널특성 분석은 수면 경로가 수신된 심볼 시간 중 에너지가 가장 강한 심볼 시간의 값을 이용하였다.

Fig. 4.

(Color available online) Baseband channel estimates of communication sequence for each bandwidth. (a) 8 kHz, (b) 16 kHz, (c) 32 kHz.

IV. 실험결과

본 연구에서 측정된 파고 데이터를 수신신호와 시간 동기화를 통해 신호가 송수신 되는 5 s 동안 변동하는 수면 움직임을 측정하였고 측정된 파고 데이터를 기반으로 해수면 스펙트럼을 도출하였다. Fig. 5(a)는 인위적 파도를 생성한 후 20 min 동안 측정된 파고 스펙트럼으로 실험 시작 후 200 s까지는 상대적으로 거친 해수면 특성으로 인하여 넓은 주파수 범위의 에너지를 갖으며 1Hz 부근에서 강한 에너지가 발생하였다. Fig. 5(b)는 통신신호가 송․수신 되는 5 s 동안 측정된 파고를 이용하여 실효치 파고를 계산한 결과이다.

Fig. 5.

(Color available online) (a) Changes in wave spectrum energy with time, (b) changes in RMS wave height with time.

Fig. 6은 8 kHz 대역폭의 통신신호에서 실효치 파고에 따른 수면 경로의 유효 도플러 확산을 비교한 그림이다. 실효치 파고가 1.1 cm인 경우의 채널의 유효 도플러 확산은 ± 0.8 Hz로 측정되었으며, 실효치 파고 5.4 cm 인 경우 유효 도플러 확산은 ± 3.5 Hz로 측정되었다. 해수면 거칠기가 증가하면 수면에서 음파산란의 영향이 증가하고 수신되는 해수면 경로의 에너지와 지연시간의 차이를 발생시킨다. 이러한 영향으로 인해 실효치 파고가 증가함에 따라 유효 도플러 확산이 증가한 것으로 추정된다.

Fig. 6.

(Color available online) Results of RMS Doppler spread by RMS wave height (8 kHz bandwidth). (a) h : 1.1 cm, σν : ± 0.8 Hz (b) h : 5.4 cm, σν : ± 3.5 Hz.

Fig. 7은 3가지 대역폭에서 로그 스케일로 표현된 레일리 파라미터와 유효 도플러 확산의 상관관계를 나타낸다. 모든 대역폭에서 수면 거칠기와 유효 도플러 확산은 양의 상관관계를 갖는 것을 확인하였으며, 선형회귀 분석을 통해 기울기(회귀계수)는 대역폭 8 kHz의 경우 0.12였으며, 대역폭 16 kHz과 32 kHz의 경우는 0.13으로 동일하였다. 16 kHz와 32 kHz는 대역폭이 증가할수록 해수면 산란의 영향이 증가하여 도플러 확산의 영향이 증가하여야 하지만, 유사한 유효 도플러 확산 분포와 동일한 회귀계수 값을 보였다. 이러한 경향이 발생한 이유는 수면 경로의 에너지가 대역폭이 증가함에 따라 여러 지연시간에 걸쳐 수신되나, 본 연구에서는 가장 강한 에너지만을 이용하여 대역폭이 증가할수록 수면 경로의 에너지가 충분히 반영되지 않았기 때문으로 추정된다. 대역폭에 따른 도플러 확산의 영향을 충분히 반영하기 위하여 수면 경로의 유효 도플러 확산에 반송 주파수와 대역폭의 비율(Fc/Bw)을 곱한 가중 유효 도플러 확산(wfσν)을 사용하여 분석을 수행하였다.

Fig. 7.

(Color available online) RMS Doppler spread as a function of Rayleigh parameter in 3 types of bandwidth. (a) 8 kHz, (b) 16 kHz, (c) 32 kHz.

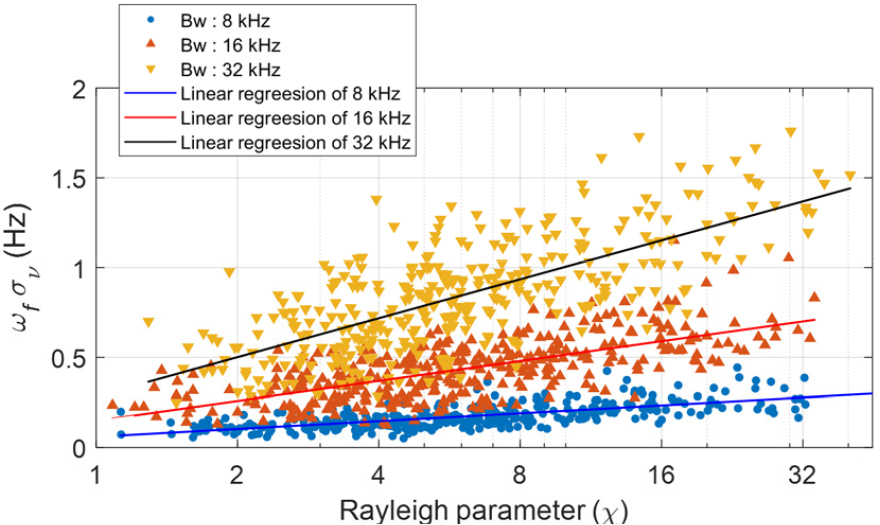
Fig. 8은 3가지 대역폭에서 레일리 파라미터와 wfσν의 상관관계 및 회귀분석 결과이다. 해수면 거칠기와 wfσν은 양의 상관관계를 갖는 것을 확인하였다. 회귀계수 추출결과 8 kHz의 경우 0.007, 16 kHz의 경우 0.018, 32 kHz의 경우 0.026으로 대역폭이 증가함에 따라 wfσν변화량도 증가하는 것을 확인하였다. 수면 거칠기에 의한 도플러 확산의 통계적 특성을 분석하기 위하여 레일리 파라미터 구간을 선정하였다. 레일리 파라미터를 1 ~ 2, 2 ~ 4, 4 ~ 8, 8 ~ 16, 16 ~ 32의 구간으로 나누었으며 각 구간별 30개 이상의 표본을 확보하였다. 각 구간에서의 wfσν의 통계적 특성(평균, 표준편차)을 추출하였다.

Fig. 8.

(Color available online) BCRσν as a function of Rayleigh parameter in 3 types of bandwidth. (a) 8 kHz, (b) 16 kHz, (c) 32 kHz.

Fig. 9는 레일리 파라미터에 따른 수면 경로의 시변 채널 파라미터의 통계적 특성 비교 결과이다. Fig. 9(a)에서는 레일리 파라미터가 증가함에 따라 모든 대역폭에서 도플러 확산의 영향은 증가하였다. 각 구간별 wfσν변화량은 32 kHz에서 가장 높았으며, 레일리 파라미터 4이후에서 대역폭에 따른 wfσν의 차이가 더욱 증가하였다. Fig. 9(b)는 레일리 파라미터에 따른 수면 경로의 상관시간(Tc)이다. 레일리 파라미터가 증가함에 따라 도플러 확산이 증가하고, 고속 페이딩이 발생하여 채널의 시간 상관성이 낮아진다. 따라서, 레일리 파라미터가 증가함에 따라 해수면 산란 영향의 증가로 Tc가 감소하였으며, 대역폭이 작을수록 높은 Tc 를 보였다. 레일리 파라미터가 8이상인 경우 상대적으로 매우 거친 거칠기로 인하여 모든 대역폭에서 낮은 Tc를 보였다.

Fig. 9.

(Color available online) (a) Average of weighted RMS Doppler spread by range of Rayleigh parameter in 3 types of bandwidth, (b) Average of coherence time by range of Rayleigh parameter in 3 types of bandwidth.

V. 결론 및 토의

본 논문에서는 수면 거칠기에 따른 해수면 경로의 시변 채널의 통계적 특성을 비교하기 위하여 수조실험을 수행하였다. 수조에서 인위적으로 발생시킨 거칠기를 용량식 파고계를 이용하여 정량적으로 측정하였으며, 128 kHz의 중심 주파수와 3가지 대역폭을 가진 통신신호(8 kHz, 16 kHz, 32 kHz)를 이용하였다. 통신신호의 반송 주파수와 대역폭에 따른 영향을 보정한 도플러 확산과 상관시간을 수면 경로의 시변 채널 파라미터로써 사용하였고, 해수면 거칠기는 실효치 파고, 주파수, 음속과 수평입사각을 반영한 레일리 파라미터를 사용하였다. 수면 거칠기에 따른 수면 경로의 시변 채널특성의 상관관계 분석을 위해 레일리 파라미터 구간을 나눈 후 wfσν와 Tc의 통계적 특성을 이용하여 분석하였다. 통계적 특성 중 평균값을 사용하여 수면 거칠기에 따른 wfσν의 상관관계를 분석한 결과 양의 상관관계를 보였다. 또한 대역폭이 증가함에 따라 도플러 확산의 영향이 증가하였으며, 레일리 파라미터 4이상에서는 대역폭 별 도플러 확산의 영향이 더 크게 증가하였다. Tc의 경우 수면 거칠기가 증가함에 따라 감소하였으며, 레일리 파라미터 8이상인 경우 Tc가 급격하게 감소하였다.

수면 거칠기는 음파의 산란을 발생시켜 통신신호에 도플러 확산, 고속 페이딩 특성을 야기한다. 따라서 수면 거칠기가 증가할수록 통신채널의 시간 상관성을 저해하여 통신신호의 길이가 채널의 변동주기보다 길어지게 되어 통신성능을 악화시킨다. 따라서 수면 경로의 상관시간을 이용하여 전체 채널의 상관시간을 모의할 수 있다면 사전에 해상상태를 고려하여 정보신호의 길이 및 채널 업데이트 주기를 선정하여 효율적으로 통신신호를 설계할 수 있을 것으로 기대된다.

본 연구에서는 수면 경로의 상관시간과 직접경로와 수면 경로 에너지의 비율(wt)을 이용하여 전체 채널의 상관시간을 모의하고 실제 측정된 전체 상관시간을 비교하였다(Fig. 10). 레일리 파라미터 1 ~ 4인 구간에서는 모의결과와 실측값의 차이가 발생하였지만, 레일리 파라미터 4이상인 경우에는 두 결과 모두 0.05 s 이하의 낮은 상관시간을 보였다. 레일리 파라미터 1 ~ 4인 구간에서 모의결과와 실측값의 차이가 발생한 이유는 실측된 전체 채널의 상관시간은 직접경로와 수면경로뿐만 아니라 수신된 모든 다중경로를 고려하여 시간 상관성을 도출하였으며, 수조의 경우 다중경로에 의한 영향이 크기 때문이다. 추후 다중경로의 영향이 적은 해상에서 실험을 수행하여 본 연구에서 제안한 방법의 타당성을 검증할 예정이다.

Fig. 10.

(Color available online) (a) Average of Weighted coherence time by range of Rayleigh parameter in 3 types of bandwidth, (b) average of coherence time of total channel by range of Rayleigh parameter in 3 types of bandwidth.

Fig. 11은 수조에서 측정된 실효치 파고에 따른 해수면 스펙트럼 에너지와 Pierson-moskowitz 모델^[19,20]을 이용하여 모의한 실효치 파고에 따른 해수면 스펙트럼 에너지를 비교한 결과이다. Fig. 11(a)는 신호가 송수신되는 5 s 동안 생성된 파고를 이용하여 해수면 스펙트럼을 계산하였기 때문에 상대적으로 고주파 성분의 에너지가 우세하게 관측되었지만, Fig. 11(b)를 통해 실제 대양에서는 1 Hz 이하의 저주파 성분의 에너지도 발생하는 것을 확인하였다. 또한 해상실험의 경우 200 s 이상의 파고 데이터를 이용^[21]하여 해수면 스펙트럼을 계산하기 때문에 저주파 성분의 에너지도 강하게 발생하지만, 본 연구에서는 수면 거칠기에 따른 고주파수 산란에 의한 영향을 비교하기 위해 저주파 성분에 의한 영향은 고려하지 않았다. 추후 해상실험을 통해 다양한 해수면 거칠기에 따른 해수면 경로 시변 채널특성의 통계적 분석을 수행하고 수조 실험 결과와 비교를 수행할 예정이다. 또한 본 연구에서 제시한 시변 채널 파라미터(wfσν,wtTc)를 실제 해양에 적용하기 위한 추가 연구를 수행할 예정이다.

Fig. 11.

(Color available online) Wave spectrum change in relation to RMS wave height. (a) tank experiment, (b) Pierson-moskowitz model.