I. 서 론

수중음향통신 시스템은 수중통신 네트워크나 자율잠수정 등의 다양한 응용분야에서 사용된다. 그러나 시스템의 모뎀이나 채널 코딩의 설계와 성능은 주어진 해양환경의 음향채널 매개변수에 의해 결정된다. 음향채널매개변수의 특징을 결정하는 채널 페이딩은 국소 채널 페이딩(small scale channel fading)과 광역 채널 페이딩(large scale channel fading)으로 구분된다. 전자는 다중경로 지연 확산에 의한 신호의 간섭, 송수신기 상대운동이나 경계면 산란 등에 의한 페이딩으로 수중음향통신 모뎀이나 채널 코딩의 기술적 설계 방법과 성능을 결정하는 페이딩이다. 후자는 송수신기 이격 거리에 따른 확산 손실과 흡수 손실에 의한 페이딩으로 수신 신호의 SNR(Signal to Noise Ratio)을 결정하므로 통신 거리를 결정하는 페이딩이다.

본 연구에서 대상으로 하는 국소 채널 페이딩은 Table 1과 같이 다중경로 지연 확산에 의해 지배되는 주파수 비 선택적 페이딩과 주파수 선택적 페이딩 및 채널의 시변(time variant due to physical changes of medium/platform)에 의해 지배되는 빠른 페이딩(fast fading; high Doppler fading)과 느린 페이딩(slow fading; low Doppler fading)으로 구분되고 실제 환경에서는 이들 4가지 페이딩의 조합으로 관측된다.^[1] 따라서 시스템을 설계하거나 성능을 평가하기 위해서는 국소 채널 페이딩에 의한 채널 매개변수를 특정하여야 한다.

Table 1. Fading mechanisms and their effects on underwater acoustic communication.

Table 1에서 지연 확산은 시간 영역에서 심벌 시간이나 등화기의 탭 수 등을 결정하고 주파수 영역에서 심벌율이나 확산 스펙트럼 방식 등화 기법 등에 관계된다.

다음으로 송수신기의 상대 운동이나 매질의 시변에 의한 채널 시변은 시간 영역에서 심벌/패킷 시간 등을 결정하고 주파수 영역에서 반송 주파수의 도플러 편이 및 심벌율을 결정하며 시변 진폭의 통계적 특성은 시간 영역 채널 코딩 기법에 관계된다.

실제 해양환경에서는 다중경로의 지연 확산과 채널시변이 결합되어 있어 상기의 다양한 채널 매개변수는 상호 독립적이지 않다. 따라서 특정의 매개변수가 실제 시스템의 설계나 성능 평가에 미치는 영향을 해석하는 것은 쉽지 않다.

국소 채널 페이딩의 채널 매개변수에 대한 연구로는 주파수에 따른 천해 수중음향채널의 통계적 특성,^[2] 채널 전파모델과 통계적 특성,^[3] 수중음향채널의 고주파수 영역 페이딩의 통계적 특성,^[4] 극천해 수중음향통신채널 특성,^[5] 천해 수중음향 채널 환경,^[6] 노르웨이 피요르드 및 발틱해 수중음향 채널 환경,^[6] 호수의 음향채널 환경^[8] 등의 연구가 있다. 기존의 천해 수평채널 연구에 의하면 2회 이상 경계면에서 반사되는 경로는 상대적으로 신호 세기가 약하게 되어 다중경로는 직접파, 해면 반사파, 해저 반사파 및 해면-해저 반사파의 4개 이하로 구성되어 있다.^{[2], [4], [5], [6], [9], [10], [11]}

채널 매개변수가 시스템의 설계 및 성능에 미치는 영향에 대한 연구로는 수중음향통신 기술 현황,^[12] 수온변화가 비코히어런트 수중통신 시스템에 미치는 영향,^[13] 다중경로 페이딩에 따른 컨벌류션 및 리드-솔로몬(Reed-Solomon, RS) 코드의 성능,^[9] 해면 산란이 직교 위상 편이 변조(Quadrature Phase Shift Keying, QPSK) 성능에 미치는 영향,^[10] 주파수 종속 다중경로 페이딩이 비코히런트 수중 통신시스템에 미치는 영향^[11]등 다양한 연구가 있다. 그러나 이들 기존 연구들은 해양환경을 단순화하거나 시스템의 성능을 제한한 것으로 다양한 수중음향통신 환경에 적응적으로 강인한 시스템에 대한 연구는 여전히 진행 중이다.

본 연구에서는 천해 송수신기 고정 시스템을 가정하여 수중음향통신 채널 모델, 채널 매개변수 수식 표현 및 측정을 위한 실험 방법을 제시한다. 아울러 실 해역 의 채널 매개변수 특성과 및 이들 매개변수가 음향통신 시스템의 설계 및 성능에 미치는 영향을 기술한다.

II. 수중음향통신 채널 모델

2.1 천해 수중음향통신 채널 모델

수중음향통신 채널의 다중 경로 파는 해면과 해저를 평면으로 가정한 평면 반사파와 경계면 거칠기에 의한 산란파로 관측된다. 해면과 같이 경계면 거칠기가 시변인 경우 산란파는 시변으로 관측된다.

본 연구에서 대상으로 하는 송수신기가 고정되어 있는 경우 파장에 비해 상대적으로 작은 매질내의 플랑크톤 등의 미세 부유물질에 의한 산란을 무시하면 수신 신호의 세기와 위상은 해면 거칠기의 시변에 동조하여 변한다.^[14]

송수신기가 상대 운동을 하면 각각의 다중경로는 서로 다른 상대속도를 갖고 각각은 서로 다른 도플러 효과에 의한 위상변화를 갖는다.

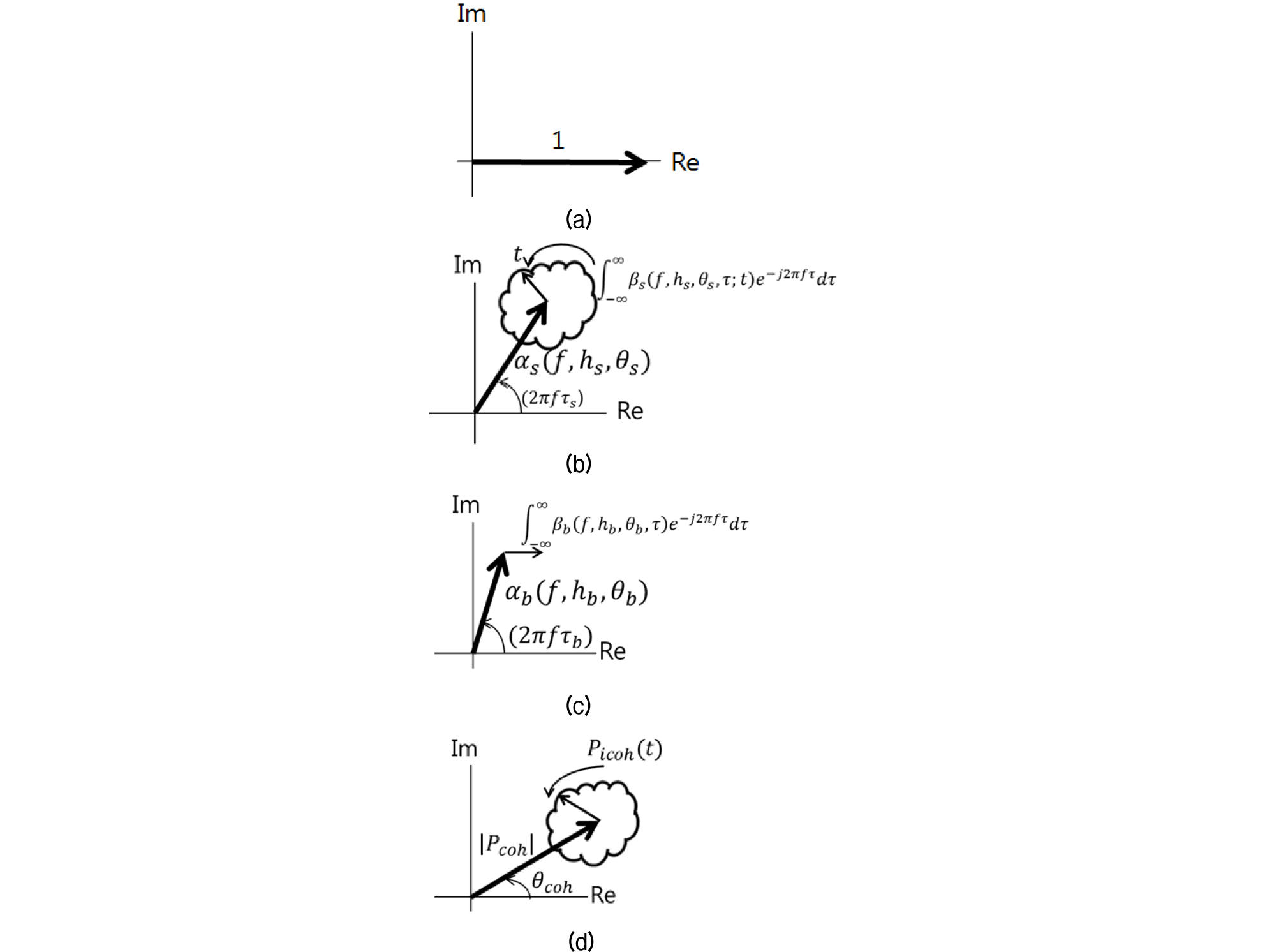
송수신기 고정의 경우 직접파, 해면 반사파 및 해저 반사파를 반송 주파수 $f$인 직접파 페이저(phasor; 복소수 진폭)로 정규화하면 각각의 페이저 $P_d,P_s\left(t\right)$ 및 $P_b$는 다음의 Eqs. (1) ~ (3)으로 주어진다. Eq. (4)는 이들 3개의 경로를 더한 신호 페이저이다.

여기서 직접파의 크기로 정규화한 Eqs. (2)와 (3)의 ${\alpha }_s(f,h_s,{\theta }_s)$와 ${\alpha }_b(f,h_b,{\theta }_b,{\rho }_b)$는 각각 해면 및 해저 반사파의 시 불변 코히어런트 평면 반사 신호 크기이며 전자의 크기는 반송 주파수($f$), 해면 거칠기 유효 높이($h_s$)와 해면 입사각(${\theta }_s$)의 함수로 ${\alpha }_s(f,h_s,{\theta }_s)=-exp[-2(k{h}_{s}sin\theta {)}^2]$이며 $k{h}_{s}sin\theta$는 Rayleigh 거칠기 매개변수 $R_{rgh}$로 정의되며 $R_{rgh}$가 작아지면 ${\alpha }_s$$(f,h_s,{\theta }_s)$는 -1에 가까워지고 커지면 0에 가까워져 산란 성분만이 존재하게 된다. 후자는 반송 주파수($f$), 해저 거칠기의 유효 높이($h_b$), 해저 입사각(${\theta }_b$) 및 저질 밀도(${\rho }_b$) 의 함수이다. ${\tau }_s$와 ${\tau }_b$는 해면과 해저 평면 반사 경로의 직접파에 대한 시간차이다. Eqs. (2)와 (3)의 ${\beta }_s(f,h_s,{\theta }_s,\tau ;t)$와 ${\beta }_b(f,h_b,{\theta }_b,{\rho }_b,\tau )$는 각각 해면과 해저 경계면 중심과 $\tau$ 지연 시간을 갖는 산란파의 크기이다.

해면 거칠기는 시변으로 해면 산란파의 적분의 크기는 시변이며 해저 거칠기는 송수신기가 고정되어 있는 경우 시 불변으로 해저 산란파 적분의 크기는 시 불변이다. 해면과 해저 거칠기에 따른 평면 반사 신호와 산란 신호의 크기는 헬름홀츠-키르히호프-프레즈넬(Helmholtz-Kirchhoff-Fresnel, HKF) 이론으로 해석할 수 있다.^[14]

Eq. (4)에서 대괄호 [ ] 성분은 $P_{coh}$성분으로 직접파, 해면과 해저면의 평면 반사 및 해저의 산란 성분이 합성된 시 불변 코히어런트 신호이고 $P_{icoh}\left(t\right)$는 해면 산란파 성분으로 시변 비코히어런트 신호이다.

Table 1의 페이딩 분류 기준과 비교하면 $P_{coh}$는 다중 경로에 의한 지연 확산 성분이고 $P_{icoh}\left(t\right)$는 매질의 시변에 의한 채널 시변 성분 이다.

동일한 다중경로 지연 ${\tau }_b$와 ${\tau }_s$에서도 반송 주파수에 따라 각각의 위상 $2\pi f{\tau }_s$와 $2\pi f{\tau }_b$가 변하므로 시 불변 코히어런트 신호의 크기 $\left|P_{coh}\right|$와 위상 ${\theta }_{coh}$는 주파수에 따라 변한다.

시변 비코히런트 신호 $P_{icoh}\left(t\right)$의 시변 위상은 반송 주파수의 도플러 확산, 시변 포락 진폭은 반송 신호의 진폭 페이딩의 통계적 분포 함수로 해석된다. Fig. 1(a) ~ 1(d)는 Eqs. (1) ~ (4)의 페이저도이다.

Fig. 1.

Phasor diagrams of multipath: (a) direct path, (b) surface bounce path, (c) bottom bounce path, (d) sum of three paths.

Fig. 1(b)에서 보는 바와 같이 해면 산란 성분은 해면의 거칠기 시변에 동조되어 변화하므로 직접파와 해면 및 해저 반사파가 합성된 Fig. 1(d)는 반송 주파수의 위상과 크기가 해면의 거칠기 시변에 동조되어 변화하며 반송 신호의 시변 포락 진폭 $\left|P\right(t\left)\right|$도 해면의 거칠기 시변에 동조되어 변한다. 페이저 $P\left(t\right)$를 실수 및 허수 성분으로 나누어 $\left|P\right(t\left)\right|$를 표현하면 다음의 Eqs. (5)와 (6)으로 표현된다.

Eq. (4)와 비교하면, $P_{coh}$와 $P(t{)}_{icoh}$는 Eq. (7)과 같다.

$m_X$와 $m_Y$가 0이면 직접파, 해면 및 해저면의 평면 반사파의 세기가 0인 상태로 우세한 다중 경로파가 없고 해면 산란파만 존재하는 경우이다. 이때 산란에 의한 실수 성분 $X1\left(t\right)$와 허수 성분 $Y1\left(t\right)$가 평균이 0인 무 상관 동일한 정규분포(complex uncorrelated Gaussian distribution)로 가정하면 $\left|P\right(t\left)\right|=X$, 즉 신호의 포락선 진폭은 Eq. (8)과 같이 Rayleigh 페이딩이 된다. $m_X$와 $m_Y$중 하나라도 0이 아니면 즉 직접파, 해면 및 해저면의 경계면 반사파의 세기가 어느 하나라도 0이 아닌 상태이면 우세한 다중경로파가 하나 이상 존재하므로 Eq. (9)와 같이 Rice 페이딩이 된다.

여기서 $I_0(sx/{\sigma }^2)$은 제1종 0차 변형 베셀함수이며 비코히어런트 산란파 전력에 대한 코히어런트 반사파 전력비를 뜻하는 Rice 인수 $K=s^2/2{\sigma }^2$에 따라 특성이 변하며 $K=0$인 상태는 산란파만 존재하는 경우로 Rayleigh 페이딩이 된다.

2.2 해면 산란 신호 모의실험

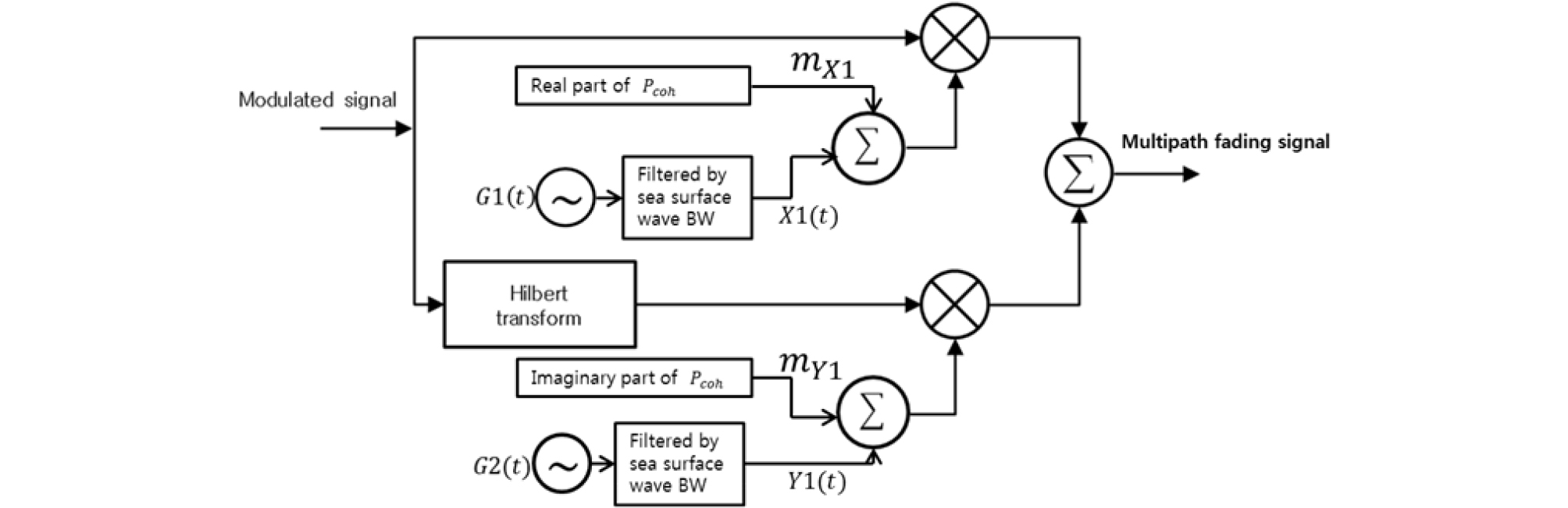
Fig. 2는 시 불변 코히어런트 평면 반사 성분과 해면 산란에 의한 시변 비코히런트 성분이 합성된 신호의 모의실험도이다.

Fig. 2.

Block diagrams of channel fading simulator of surface scattering.

Fig. 2에서 $G1\left(t\right)$와 $G2\left(t\right)$는 무 상관 가우시안 잡음이며 가우시안 잡음은 파도의 우세 주파수를 차단주파수로 하는 버터워스 저역통과 필터를 통과한다. 저역통과 된 각각의 신호가 Eq. (5)의 $X1\left(t\right)$와 $Y1\left(t\right)$에 대응되는 시변 해면 산란파 성분이다. 낮은 샘플링 주파수로 발생된 저주파수 영역 해면산란 성분은 선형보간법으로 업-샘플링 된 후 높은 샘플링 주파수로 발생된 디지털 변조 신호의 진폭이 되도록 하였다. $m_{X1}$과 $m_{Y1}$은 Eq. (5)의 다중 경로의 시불변 코히어런트 성분이다.

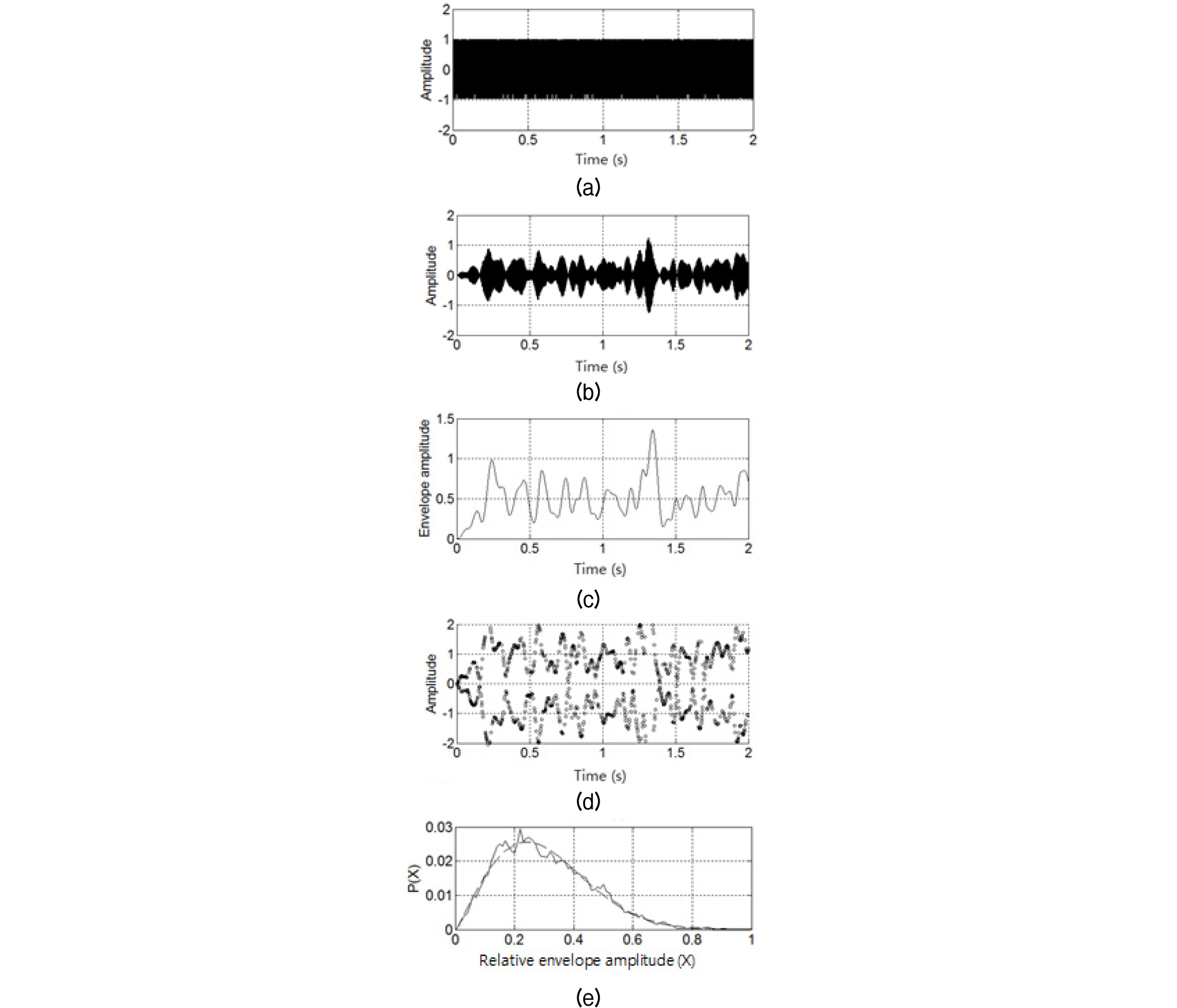
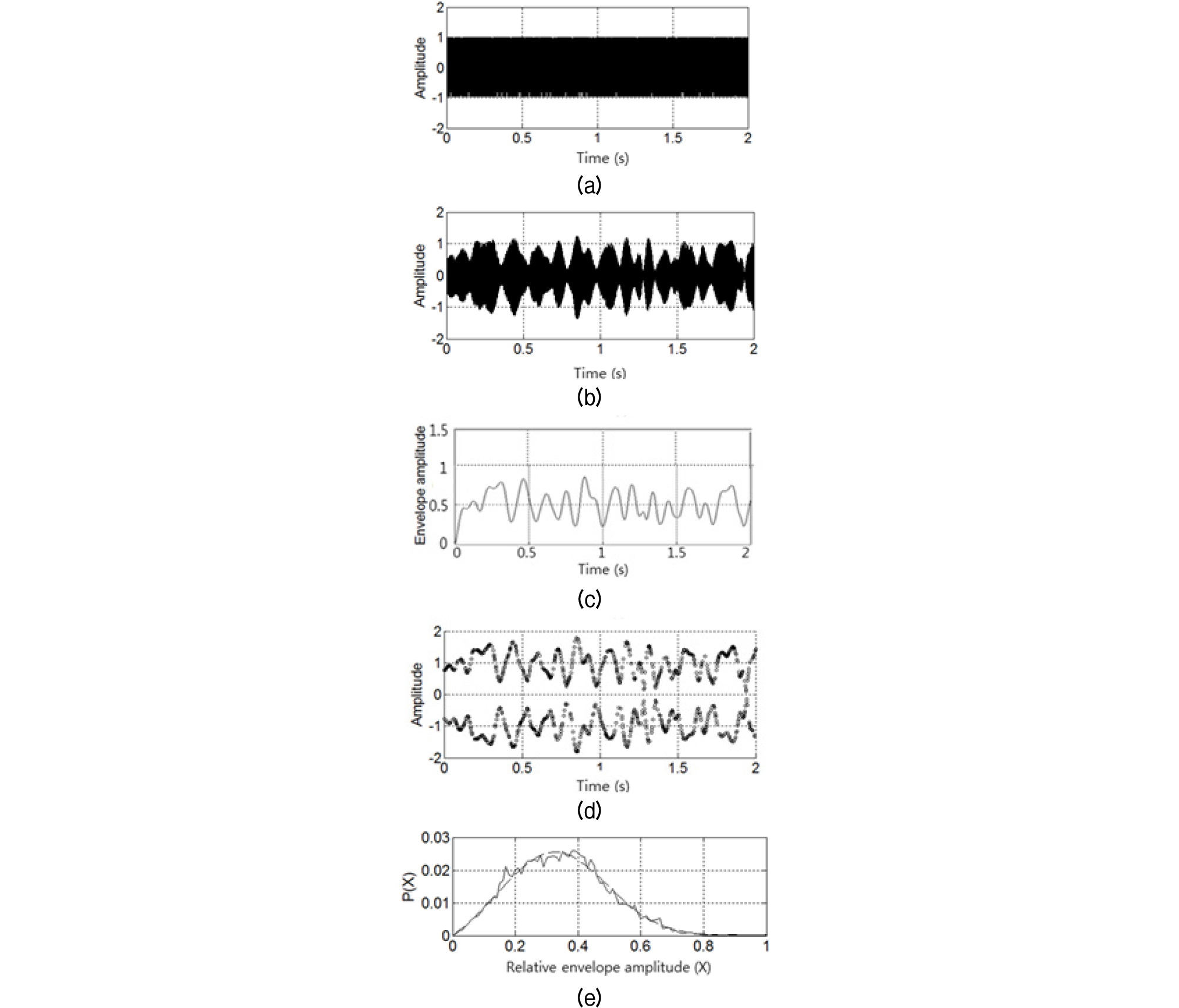
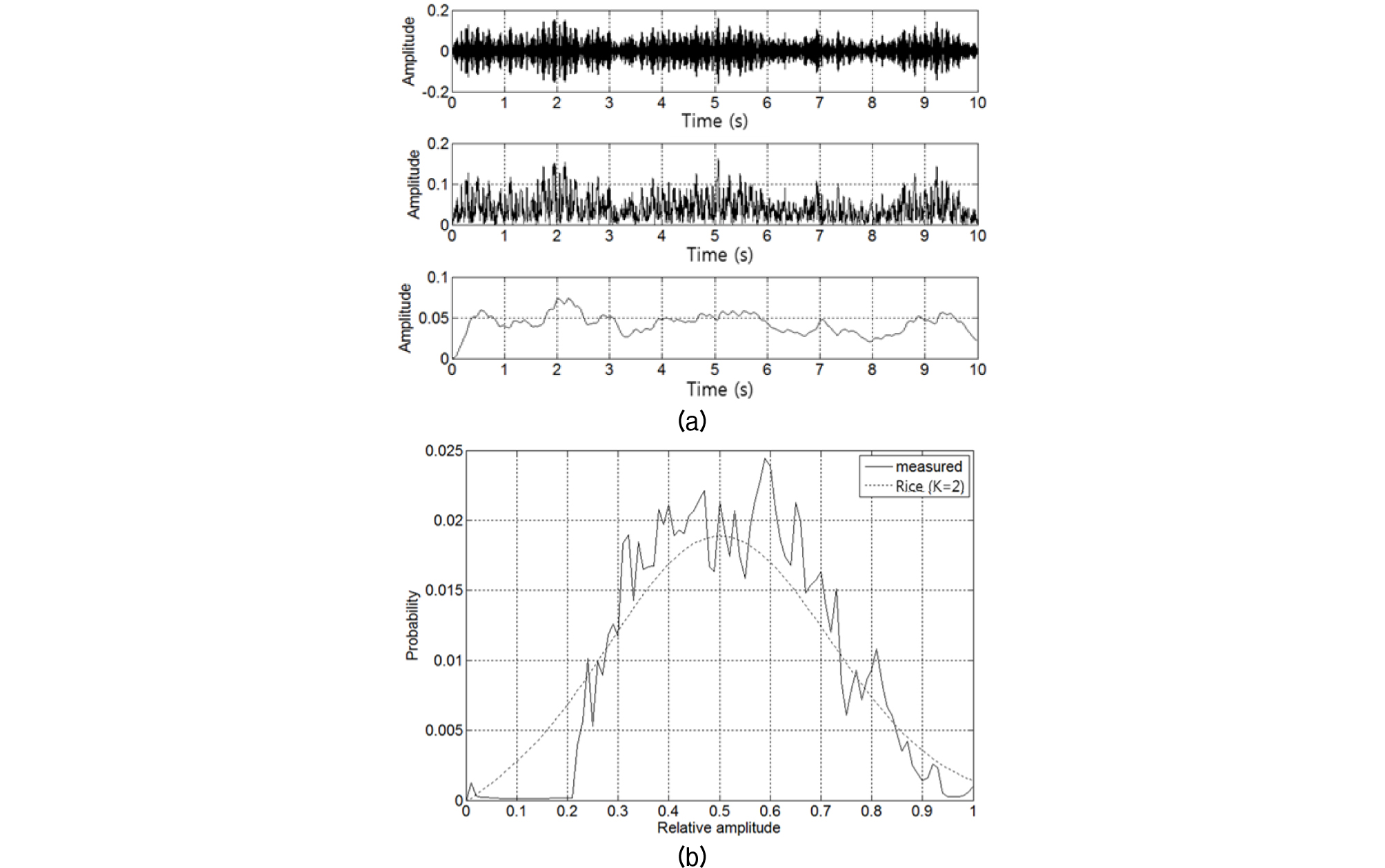
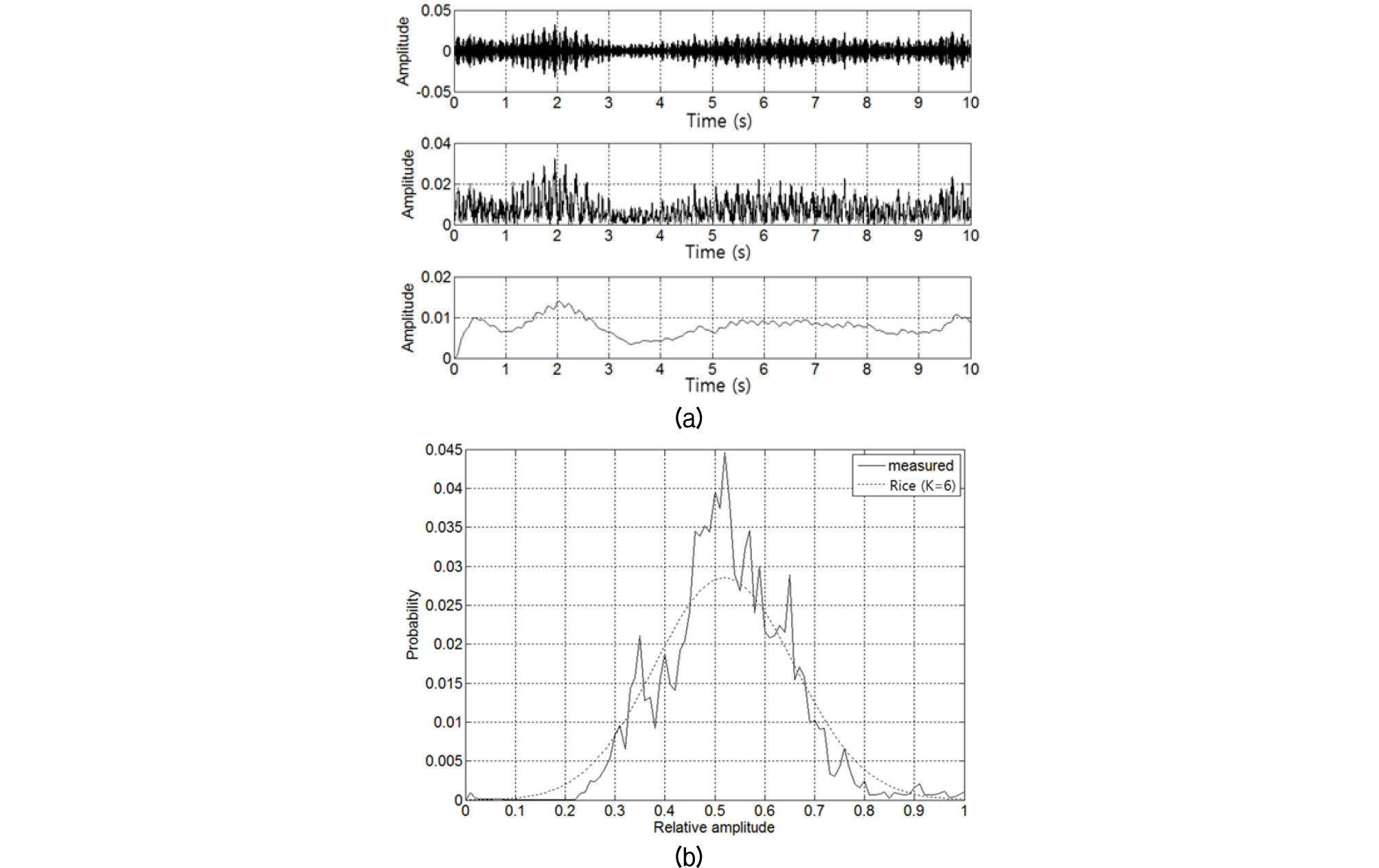
Figs. 3과 4는 반송 주파수 10 kHz인 BPSK(Binary Phase Shift Keying)신호가 파도의 우세 주파수 범위가 0 Hz ~ 3 Hz인 해면에서 산란되는 경우의 Rayleigh 페이딩과 Rice 페이딩을 모의한 시간 파형 및 포락 진폭 페이딩의 통계적 분포 함수이다.

Fig. 3.

Rayleigh fading signal and its statistics (from the top): (a) BPSK transmitting signal, (b) Rayleigh fading receiver signal, (c) its envelope, (d) demodulated signal and (e) Rayleigh probability density function of the envelope.

Fig. 4.

Rice fading signal and its statistics (from the top): (a) BPSK transmitting signal, (b) Rayleigh fading receiver signal, (c) its envelope, (d) demodulated signal and (e) Rice probability density function of the envelope.

각 그림의 위로부터 BPSK 전송신호, 해면 산란에 의한 페이딩 신호, 해면 산란 시변 포락 진폭, 페이딩 신호를 복조한 파형 및 포락 진폭의 분포함수이다. Rice 페이딩의 분포함수는 K = 1로 하여 모의하였다. 포락 진폭과 복조 파형이 잘 일치함을 알 수 있다.

따라서 페이딩은 해면 산란 파형과 같이 동조하여 변하는 특성을 보일 것이다. 실제 해상의 해면 거칠기는 Pierson-Moskowitz 파도 스펙트럼에 따라 변하며 파도 스펙트럼의 우세 주파수는 약 5 Hz 이하이며 일반적으로 풍속이 낮아질수록 우세 주파수는 커지고 대역은 넓어지므로 해면 산란시변 포락 진폭도 해면파도에 따라 동조하게 된다.^{[14], [15]} 해상 실험 자료에 대한 분포함수는 5.6절에서 제시한다.

III. 천해 수중음향통신 채널 매개변수

송수신기가 고정된 천해 수중음향통신 채널에서 Eq. (4)와 Fig. 1(d)로 표현되는 수신 신호의 페이저는 주파수, 해면과 해저 거칠기, 해저 물성이나 다중경로의 간섭 등의 음향 채널 환경에 따라 변한다. 따라서 모뎀이나 채널 코딩 설계를 위해서는 이들과 관련되는 채널 매개변수 해석이 요구된다.

본 연구에서는 1 s 주기(T = 1 s)로 60개의 시험 신호 펄스 $p\left(t\right)$를 전송하여 각 펄스 전송시각 $t$에 대한 임펄스 응답 추정치 $\hat{h}(t,\tau )$를 구하여 채널 매개변수들을 해석하였다.

임펄스 응답 $\hat{h}(t,\tau )$을 구하기 위해 자기 상관 함수가 Dirac 델타 함수와 유사한 특성을 갖는 LFM(Linear Frequency Modulation) 혹은 PN(Pseudo Noise) 신호를 사용하였다.

LFM 신호 단위 길이는 500 ms이고 500 ms의 휴지기가 부가하였고 주파수 대역은 13 kHz에서 23 kHz까지의 10 kHz이다. PN 신호 단위 길이는 비트 시간 0.1 ms인 1023비트 8개 코드 그룹을 반송파 18 kHz의 BPSK로 변조한 신호로 PN 신호 길이는 약 818 ms이며 182 ms의 휴지기가 부가되어 있고 주파수 대역은 LFM 신호와 동일하다.

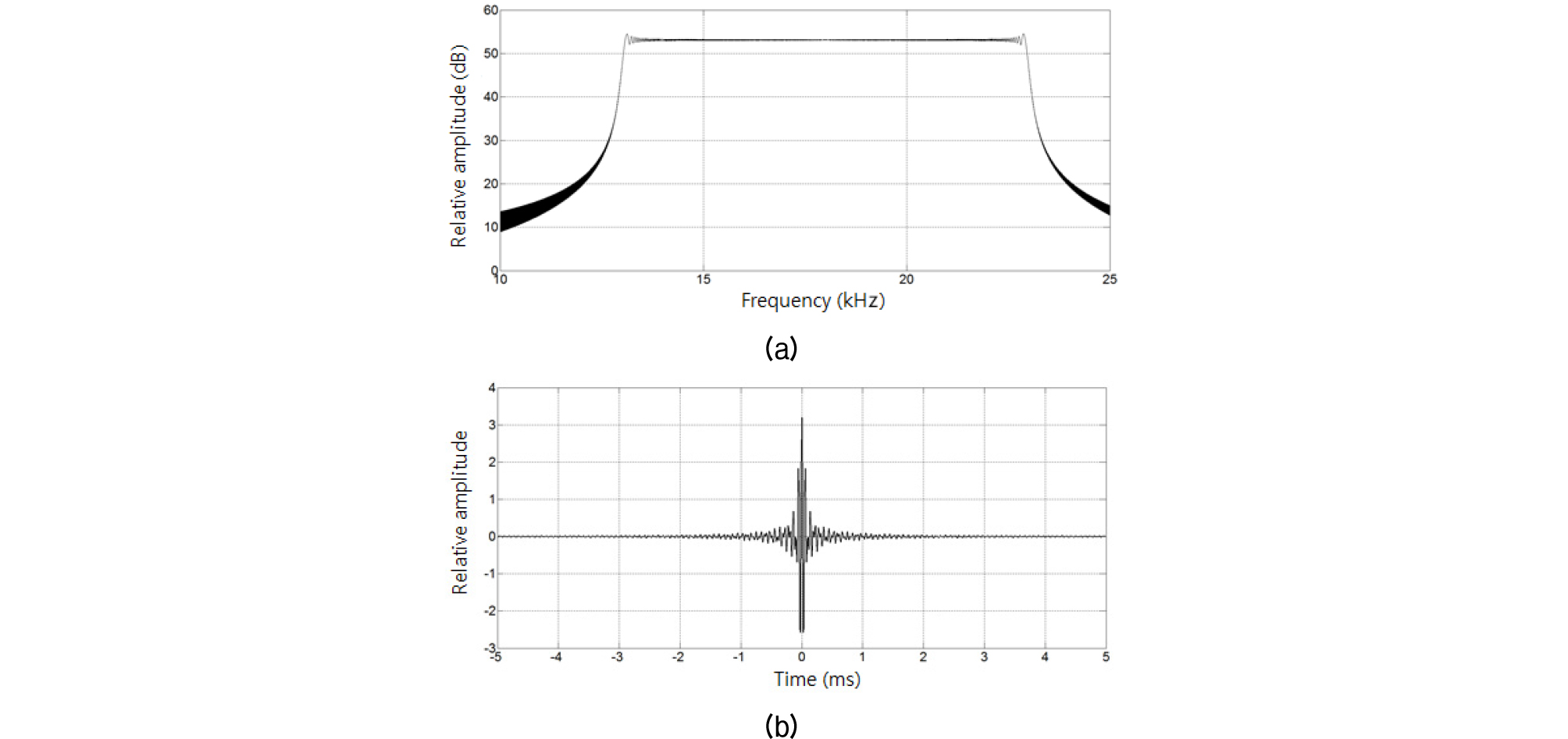
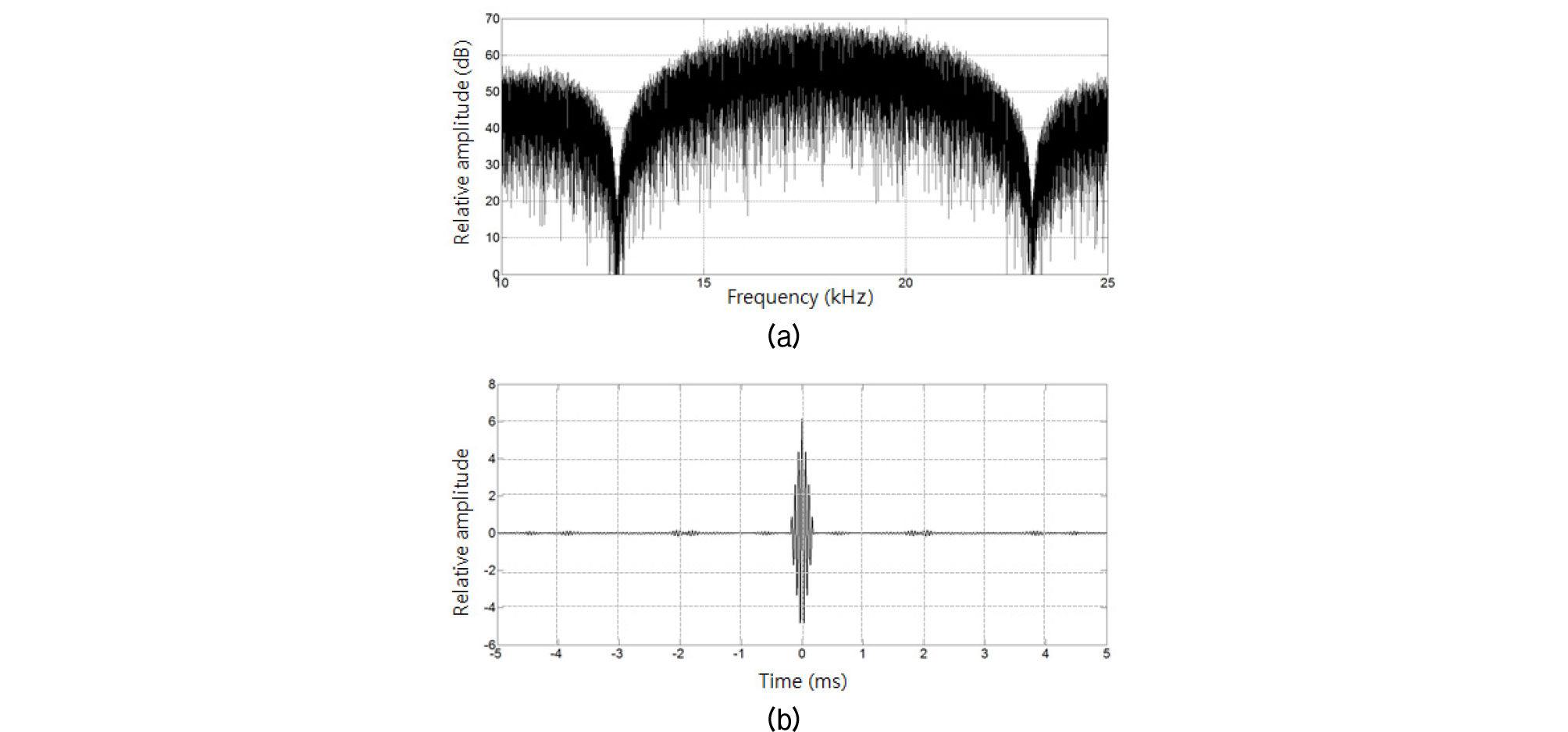
Figs. 5과 6은 각각 사용한 LFM과 PN 신호의 주파수 대역 및 자기상관 함수 특성이다.

Fig. 5.

LFM probe signal characteristics: (a) spectrum and (b) autocorrelation function.

Fig. 6.

PN probe signal characteristics: (a) spectrum and (b) autocorrelation function.

Figs. 5과 6에서 보는 바와 같이 LFM이 상대적으로 평탄한 대역 특성을 갖고 상관시간이 짧다. 각각의 자기상관 함수의 반 전력 폭은 약 0.2 ms 이내로 0.2 ms 이상의 시간차를 갖는 다중경로는 해석할 수 있을 것으로 판단된다. 그러나 반 전력 폭 특성과 음의 상관 값에 의해 델타함수 특성과는 달라 해상 실험 자료 분석 결과도 실제 임펄스 응답과는 차이를 보일 것으로 판단된다.

3.1 임펄스 응답과 자기상관 함수

수신된 LFM 혹은 PN 신호를 각각의 전송된 신호와 정합 필터 처리한 다음의 Eq. (10)은 각 전송 시각 $t$의 임펄스 응답 $\hat{h}(t,\tau )$이다.

여기서 $r\left(t\right)$는 수신 신호이다. 임펄스 응답 $\hat{h}(t,\tau )$가 전송시각 $t$에 대해 WSS(Wide Sense Stationary)하고 수신기에 도달하는 산란 성분이 무상관 US(Uncorrelated Scattering) 조건이면 임펄스 응답의 자기상관 함수의 기대 값 $E\left[\hat{h}\right(t,{\tau }_1\left)\widehat{h^{*}}\right(t+\Delta t,{\tau }_2]$는 다음 식으로 주어진다.^[16]

여기서 $\Delta t$는 각 임펄스 응답 시각 차이이다.

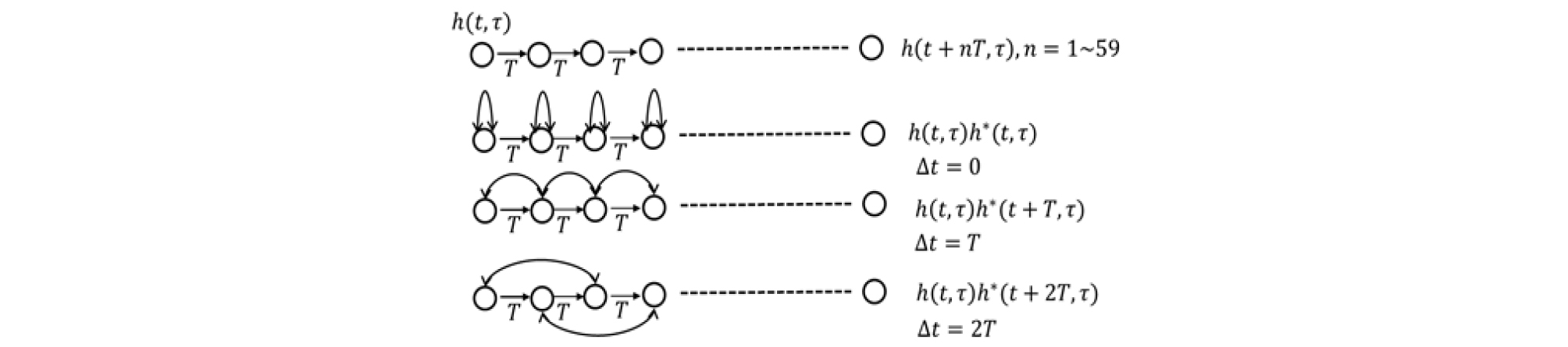
Fig. 7은 임펄스 응답 측정 시각과 이들의 시각차에 대한 Eq. (11)의 자기상관 함수를 구하는 과정이다. 시험 신호 전송시각에 따른 임펄스 응답 및 각 임펄스 응답간의 시각 차이에 대한 자기상관 함수 표본들을 나타내었다.

Fig. 7.

Impulse response measurement time and autocorrelation sample function as a function of probe signal transmission time difference.

$\Delta t=0$인 조건의 각 임펄스 응답의 지연시간 $\tau$에 대한 세기의 조화평균은 다중경로 지연 확산 $\hat{I}\left(\tau \right)$로 Eq. (12)와 같다.

3.2 채널 산란 함수

각 시험신호의 전송지연 $\tau$에 대한 임펄스 응답의 자기상관 함수 $R_{hh}(\Delta t,\tau )$에 대한 푸리에 변환은 채널의 산란 함수 $\hat{S}(\lambda ,\tau )$로 Eq. (13)로 정의된다.^{[5], [7], [16]}

본 연구에서는 T = 1 s로 하여 60개의 시험 신호 펄스 $p\left(t\right)$를 전송하여 $\Delta t$는 59 T까지로 가능하다. 그러나 Fig. 7에서 보는 바와 같이 $\Delta t$가 증가하면 표본수가 감소한다. 실험 자료의 분석은 $\Delta t$를 24 T까지로 하여 표본 수는 35개 ~ 60개의 범위를 갖도록 하였다.

산란 함수 $\hat{S}(\tau ,\lambda )$의 전송지연 $\tau$에 대한 적분은 도플러 확산 스펙트럼 $\hat{D}\left(\lambda \right)$로 Eq. (14)와 같고 채널의 최대 도플러 주파수 및 상관 시간 해석 함수이다.

Eq. (15)는 산란 함수 $\hat{S}(\tau ,\lambda )$의 확산 주파수 $\lambda$에 대한 적분으로 Eq. (12)의 다중경로 지연 확산 $\tilde{I}\left(\tau \right)$와 같게 된다.

Eqs. (10) ~ (15)의 시간 및 주파수 영역 채널 페이딩의 기준식으로부터 모뎀이나 채널 코딩 설계를 위한 다양한 채널 매개변수 해석이 이루어진다.

3.3 도플러 확산 스펙트럼과 상관시간

채널의 상관 시간은 Table 1에서 보는 바와 같이 심벌 시간을 결정하는 매개변수이다. 도플러 확산 스펙트럼 $\hat{D}\left(\lambda \right)$, 도플러 확산 평균치 $\overline{\lambda }$와 유효치 ${\lambda }_{eff}$ 및 상관 시간 $T_{coh}$과의 관계는 Eqs. (16) ~ (18)과 같다.^{[1], [5]}

도플러 확산 주파수가 커지면 상관 시간이 짧아진다.

3.4 상관 대역폭

3.4.1 지연 확산 시간 영역 특성과 상관 대역폭

채널의 상관 대역폭은 Table 1에서 보는 바와 같이 심벌율을 결정하는 매개변수이다. 채널의 상관 대역폭 $B_c\left(\Delta f\right)$는 서로 다른 주파수 성분이 동일한 진폭과 선형적인 위상 변화를 갖는 대역폭으로 심벌율이 $B_c\left(\Delta f\right)$보다 크게 되면 주파수 선택적 페이딩 채널로 정의된다.

지연 확산 $\hat{I}\left(\tau \right)$, 지연 확산 평균치 $\overline{\tau }$와 유효치 ${\tau }_{eff}$ 및 상관 대역폭 $B_c\left(\Delta f\right)$과의 관계는 Eqs. (19) ~ (22)와 같다.^{[1], [5]}

지연 확산 유효치 ${\tau }_{eff}$와 상관 대역폭 $B_c\left(\Delta f\right)$와의 관계는 서로 다른 정현파의 주파수 전달함수의 상관 계수가 0.5일 때는 Eq. (22), 상관 계수가 0.9일 때는 Eq. (23)이 적용된다.^[1]

지연 확산이 커지게 되면 주파수 영역의 동일한 진폭과 선형 위상 주파수 폭이 작아져 $B_c\left(\Delta f\right)$는 작아지게 된다.

3.4.2 지연 확산 주파수 영역 특성과 상관 대역폭

지연 확산 $\hat{I}\left(\tau \right)$의 스펙트럼 Eq. (23)은 채널의 주파수 상관 함수 $B\left(\Delta f\right)$로 정의되며 서로 다른 주파수 성분과의 진폭과 위상 변화 특성이다.^[16]

상관 대역폭 $B_c\left(\Delta f\right)$는 $B\left(\Delta f\right)$에서 진폭 변화가 -3 dB 혹은 -6 dB를 갖는 대역폭으로 정의된다.

3.5 진폭 포락 페이딩 통계적 분포 함수

채널 페이딩 통계적 특성은 Eq. (6)의 시변 포락 진폭 $\left|P\right(t\left)\right|$에 대한 통계적 특성으로 시변 포락 진폭은 수신 신호의 힐버트 변환으로 구한다. Figs. 3과 4에서 보는 바와 같이 BPSK 복조 파형으로부터 시변 포락 진폭을 구할 수도 있으나 이 경우 주파수 비 선택적인 조건으로 전송해야하며 아울러 반송주파수가 보상 간섭 혹은 상쇄 간섭 주파수 등 주파수 변화에 따른 분포함수 해석에 제한점이 따른다.

본 연구에서는 앞서 기술한 10 kHz 대역(13 kHz ~ 23 kHz)의 1 s PN 단위 시험 신호 60개를 전송하고 수신 신호를 힐버트 변환하여 구한 진폭 포락의 통계적 분포 함수를 해석하였다. LFM 신호는 시간에 따라 주파수가 변하므로 시변 채널 페이딩 해석에는 부적합하다.

시 불변 성분의 크기($s=\sqrt{m_{X1}^2+m_{Y1}^2}$)는 다중경로 간섭에 의해 변하고 시변 산란 성분 크기($\sigma =\sqrt{X1(t{)}^2+Y1(t{)}^2}$) 역시 주파수에 따라 변하므로 통계적 분포 함수는 주파수에 따라 변할 것이다.

IV. 해상 실험

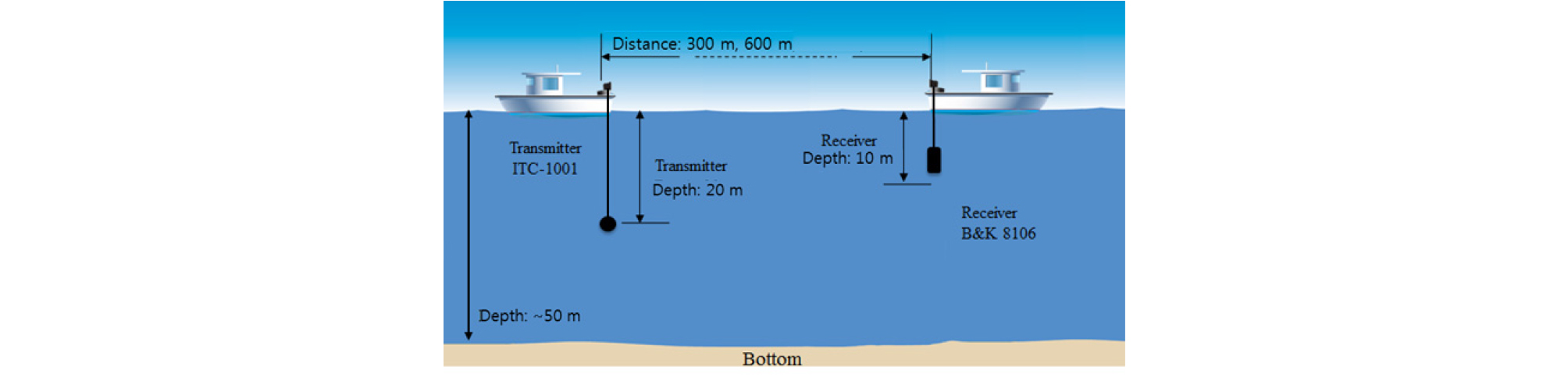
Fig. 8은 2016년 9월 25일 부산 해운대 앞 바다에서 수행한 해상 실험도이다. 실험 해역의 수심은 약 50 m 이고 해저 저질은 사니질이다. 해양기상청이 실험 해역에 설치한 해양 자료 수집용 부이 자료에 의하면 실험 당시 유효파고는 0.5 m이며 우세파의 주기는 약 4 s로 주파수는 0.25 Hz 이다. 송수신기의 거리는 300 m와 600 m로 하였다. 송신기와 수신기의 깊이는 각각 20 m와 10 m로 수심에 대해 비대칭적으로 하여 다중 경로 각각의 경로 길이가 다르게 하였다.

Fig. 8.

Experimental configuration.

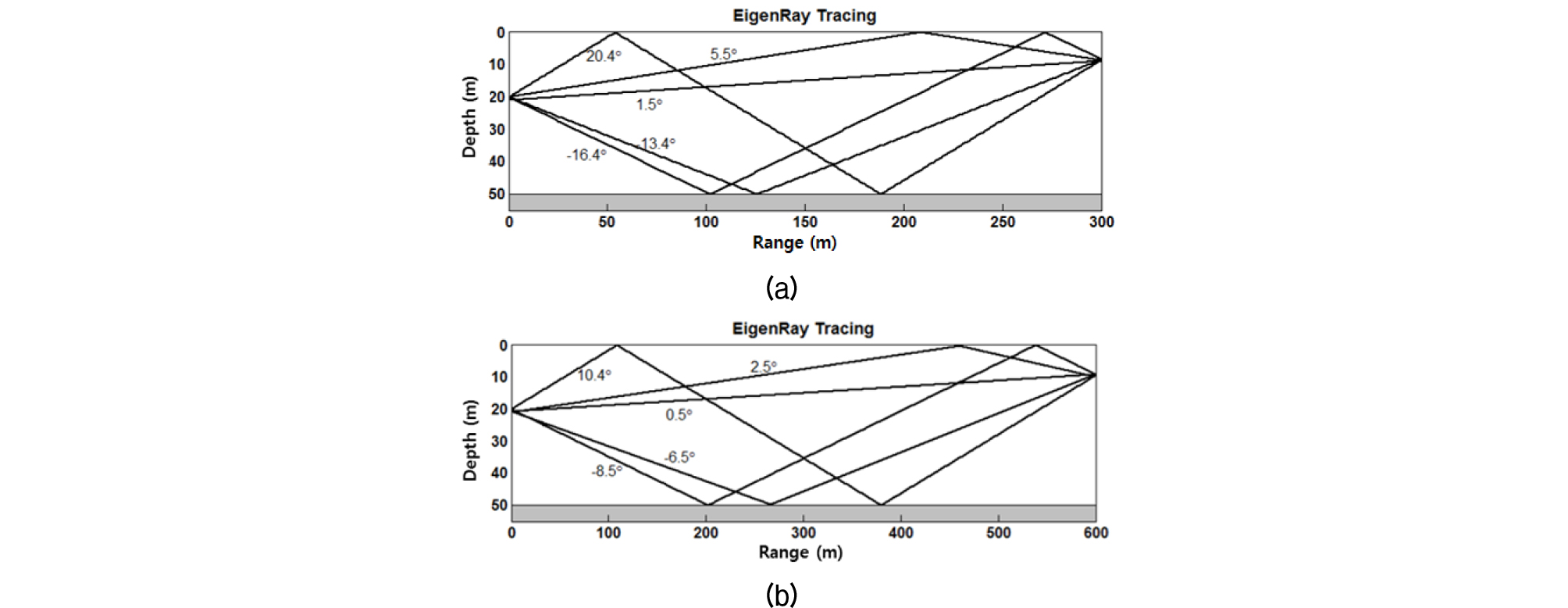
Fig. 9는 송수신기 거리가 300 m와 600 m의 5개 다중경로의 고유음선으로 현장에서 측정한 수심별 음속 자료를 이용하여 구하였다. 각 고유음선에 표시된 수치는 각 음선의 경계면 입사각이며 직접파는 수평면에 대한 각도이다. Table 2는 반사 경로에 따라 각각의 고유음선을 구분한 직접파 기준의 각각의 지연시간과 경계면 입사각이다.

Fig. 9.

Eigenray trace results in source-to-receiver ranges; (a) 300 m and (b) 600 m.

Table 2. Relative time delay and first bounce grazing angle of each eigenray in 300 m and 600 m source- to-receiver ranges (D: direct, B: bottom bounce, S: surface bounce).

V. 해상 실험 결과

5.1 임펄스 응답과 지연 확산

Figs. 10과 11은 각각 LFM 시험 신호를 이용한 수신 신호에 Eq. (10)을 적용하여 구한 송수신기 거리 300 m와 600 m의 시험 신호 전송 시각에 대한 임펄스 응답 추정치 $\hat{h}(t,\tau )$와 Eq. (11)을 적용한 지연확산이다.

Fig. 10.

Impulse response delay spreading using LFM signal at 300 m source-to-receiver range (from the top): (a) sample impulse response, (b) absolute impulse responses as a function of transmission, and (c) delay spreading.

Fig. 11.

Impulse response delay spreading using LFM signal at 600 m source-to-receiver range (from the top): (a) sample impulse response, (b) absolute impulse responses as a function of transmission, and (c) delay spreading.

임펄스 응답은 가장 먼저 수신되는 직접파의 전송 경로 시변은 없다고 가정하고 직접파의 수신 시각을 1 ms로 조정하여 제시하였다. ITC-1001 송신기의 주파수 응답은 약 18 kHz에서 최대 응답을 보이며 수직 방향 지향성을 갖는다.

따라서 송신기의 주파수 응답, 측정선의 운동에 의한 송신기의 상하 운동 및 Fig. 5에서 보이는 LFM 신호의 자기 상관함수 특성에 의해 실제의 채널 임펄스 응답과 일치하지는 않을 것이다.

Fig. 10의 300 m의 임펄스 응답을 Table 2와 비교하면 직접파와 해면 반사파가 상대적으로 강하게 수신됨을 알 수 있고 그 이외의 해저 반사파와 2회 이상 해면 혹은 해저에서 반사되는 음선은 해저 경계면 입사각이 커서 해저 손실이 크게 되어 관측되지 않는다. Fig. 11의 600 m의 임펄스 응답을 Table 2와 비교하면 직접파와 해면 반사파 및 해저 반사파가 상대적으로 강하게 수신됨을 알 수 있고 그 이외의 2회 이상 해면 혹은 해저에서 반사되는 음선은 경계면 입사각이 커서 관측되지 않는다. 해저 경계면 입사각이 10^o이고 사니질인 경우 24 kHz의 반사손실은 약 6 dB ~ 10 dB로 알려져 있다.^[17]

전체적으로 직접파의 세기는 시 불변특성으로, 해면 반사파는 시변 특성으로 관측되며 Table 2의 고유음선 지연시간 예측 치와 실측치와의 오차는 고유음선 예측을 위한 음속 자료 및 수심 오차에 의한 것으로 판단된다

1 s 주기의 단위 시험 신호는 LFM 500 ms에 휴지기 500 ms가 부가되어 있다. 그러나 최대 지연 확산은 10 ms의 수배 이하에 불과하므로 시간 분해능을 높이기 위해 주기를 짧게 하는 것도 가능하다. 예를 들면 LFM 신호 100 ms에 휴지기 100 ms로 하여 200 ms의 단위 신호를 전송하는 것이다. LFM 신호의 최소 길이는 LFM 신호의 최소 주파수와 최대 지연 확산에 의해 결정된다.

5.2 채널 산란 함수

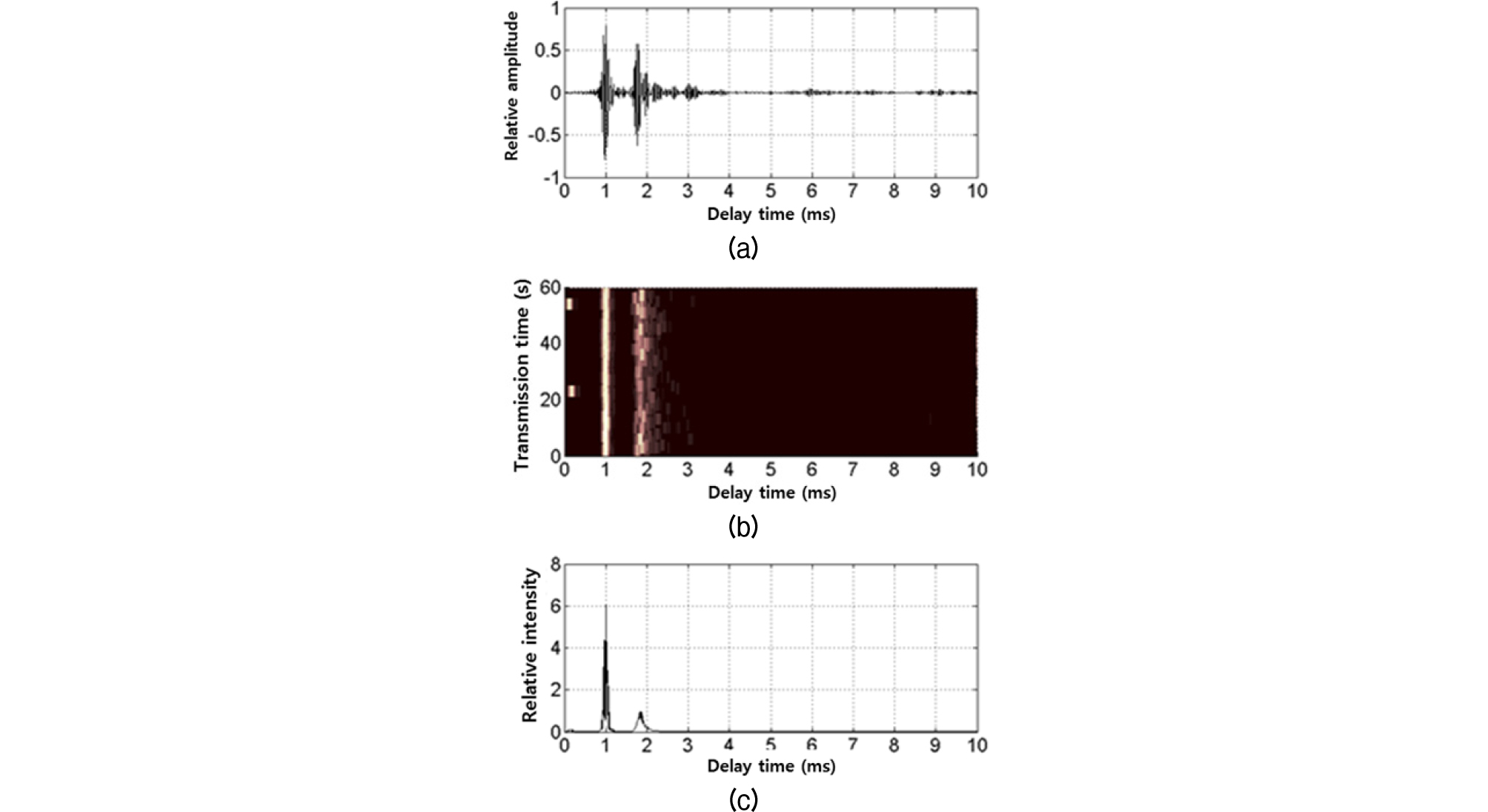
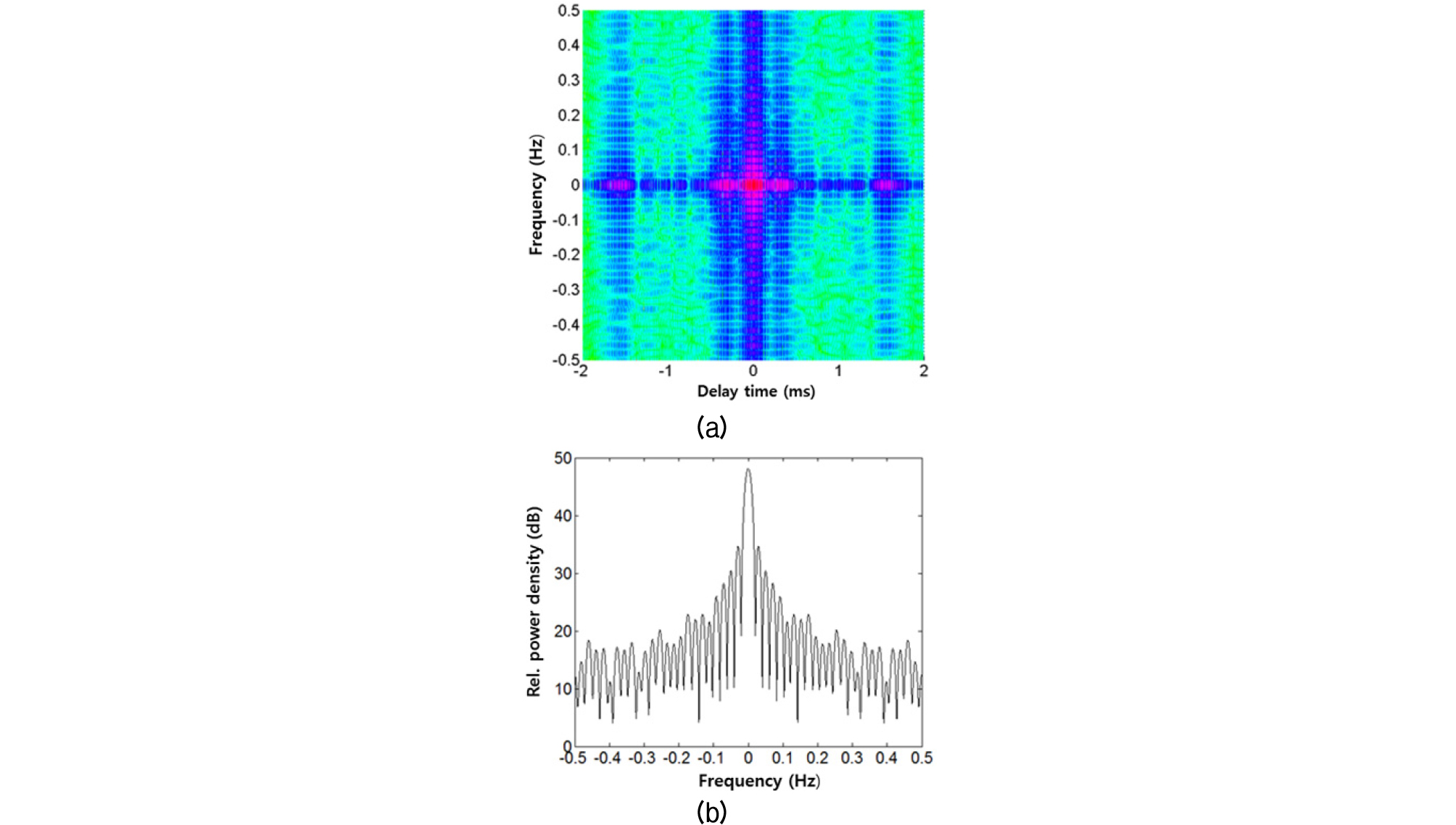
Figs. 12와 13은 각각 Eq. (11)을 이용한 송수신기 거리 300 m와 600 m의 자기 상관함수이다. $\Delta t$의 범위는 -24 T ~ 24 T이다.

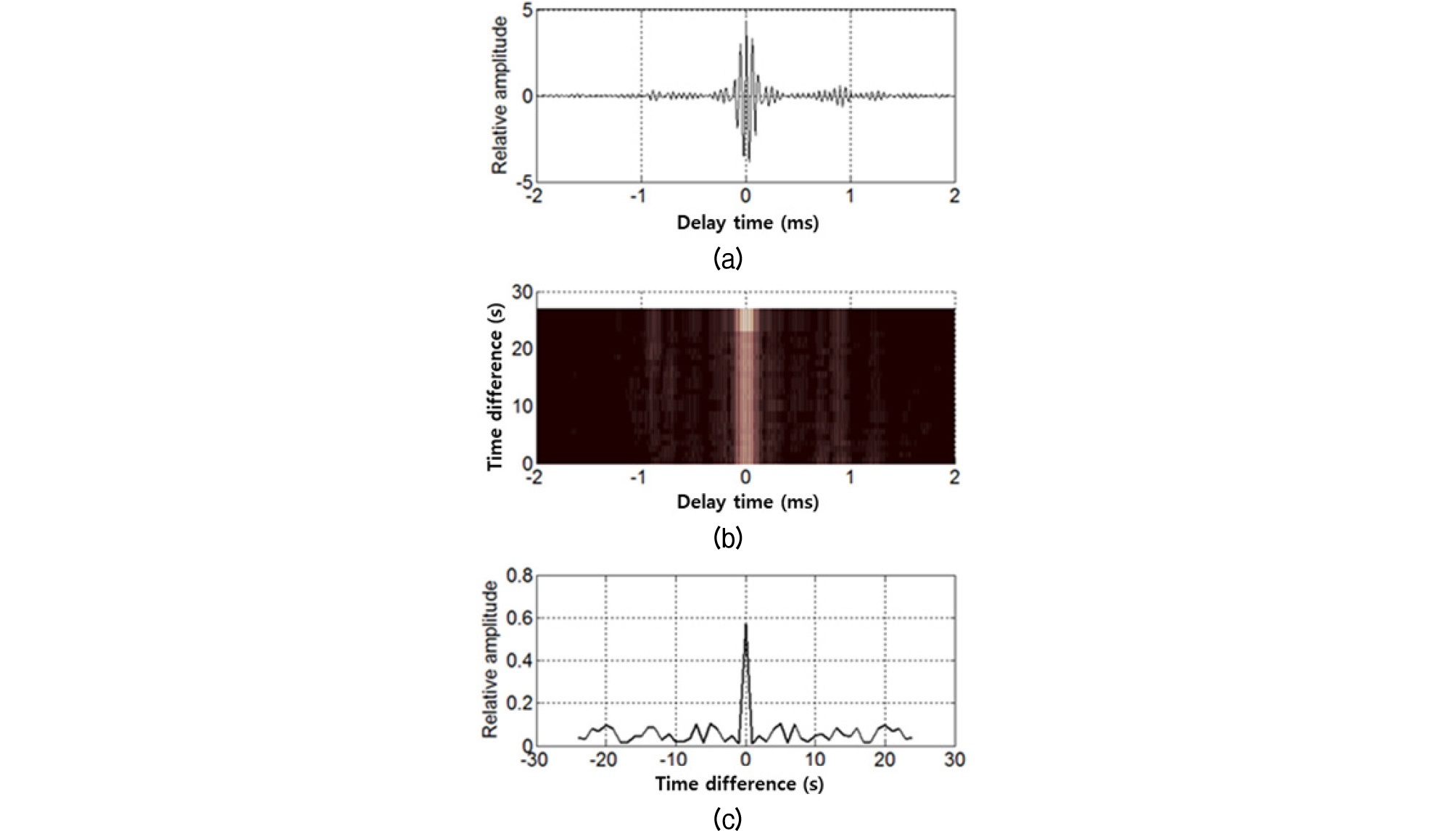
Fig. 12.

Autocorrelation function of impulse response at 300 m source-to-receiver range (from the top): (a) sample autocorrelation function of a given time difference, (b) absolute value of autocorrelation function as a function of time delay and time difference, and (c) autocorrelation function as a function of time difference.

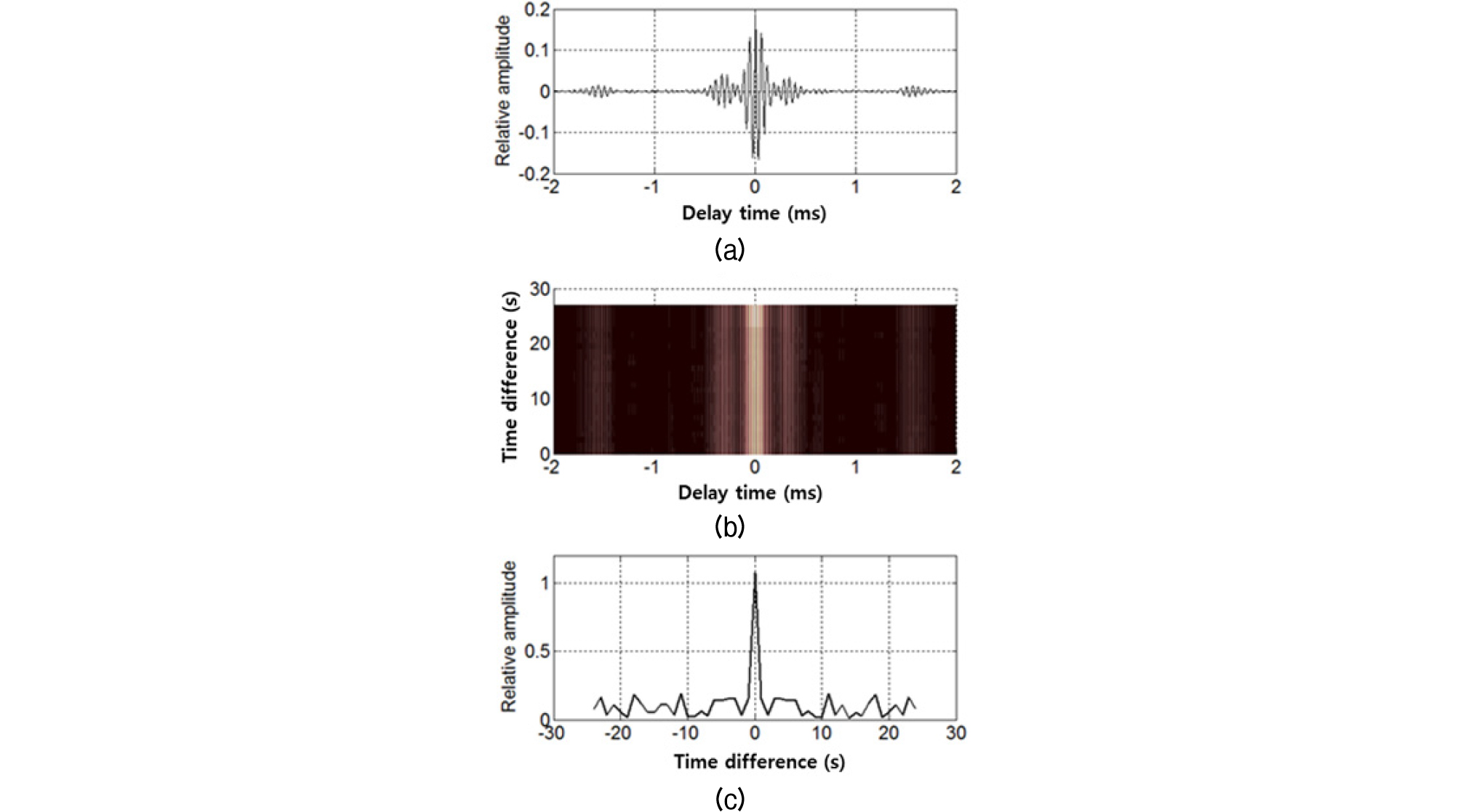
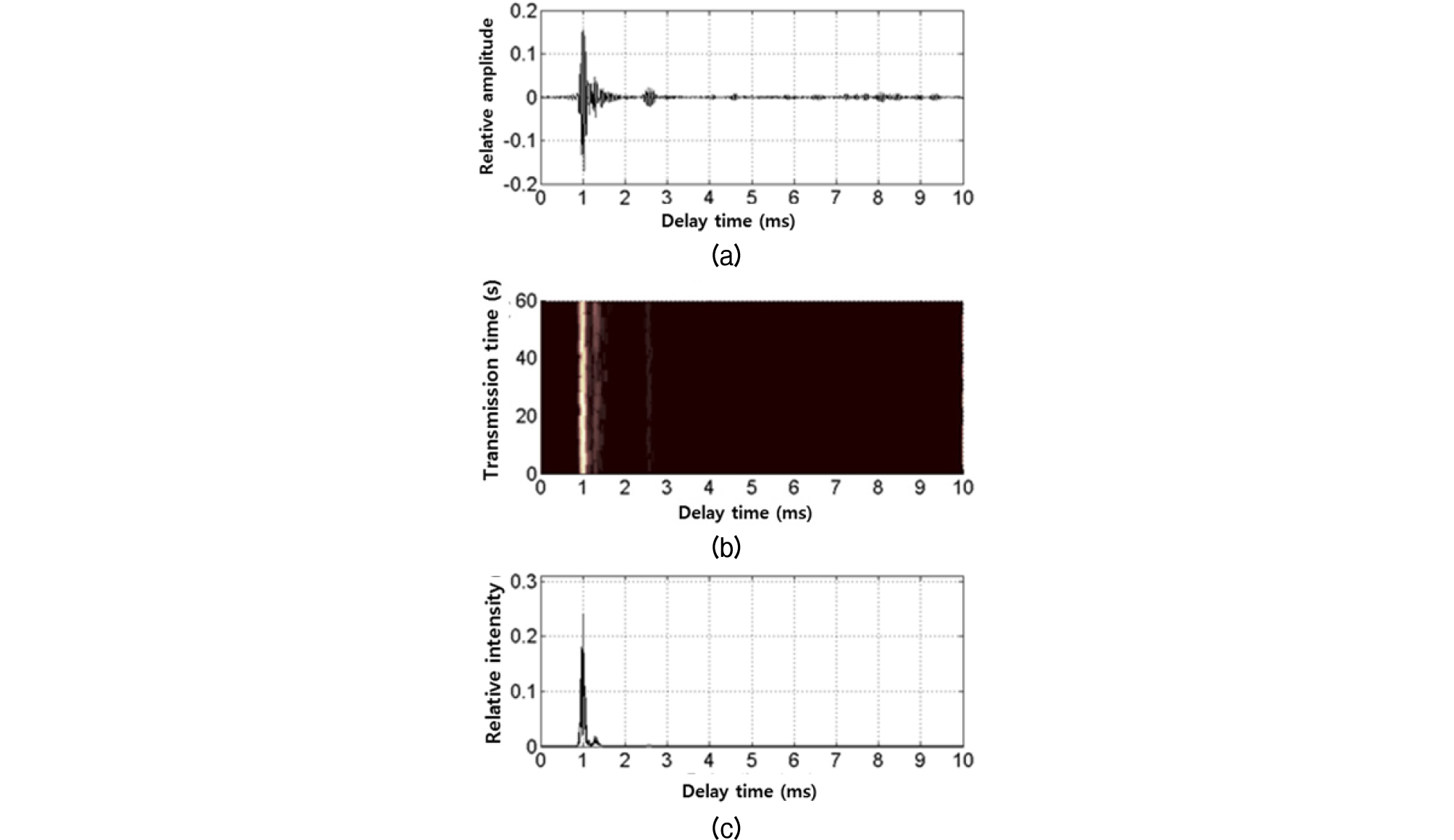
Fig. 13.

Autocorrelation function of impulse response at 600 m source-to-receiver range (from the top): (a) sample autocorrelation function of a given time difference, (b) absolute value of autocorrelation function as a function of time delay and time difference, and (c) autocorrelation function as a function of time difference.

직접파의 세기가 강하여 각각의 상관 함수는 지연시간 $\tau =0$에서 최대치를 보이고 아울러 시간차 $\Delta t=0$인 경우 상관 함수는 최대치를 보이며 시간차 증가에 따라 일정한 수준으로 변동하는 특성을 보인다. 이러한 특성은 해면의 산란에 의한 것으로 해석된다.

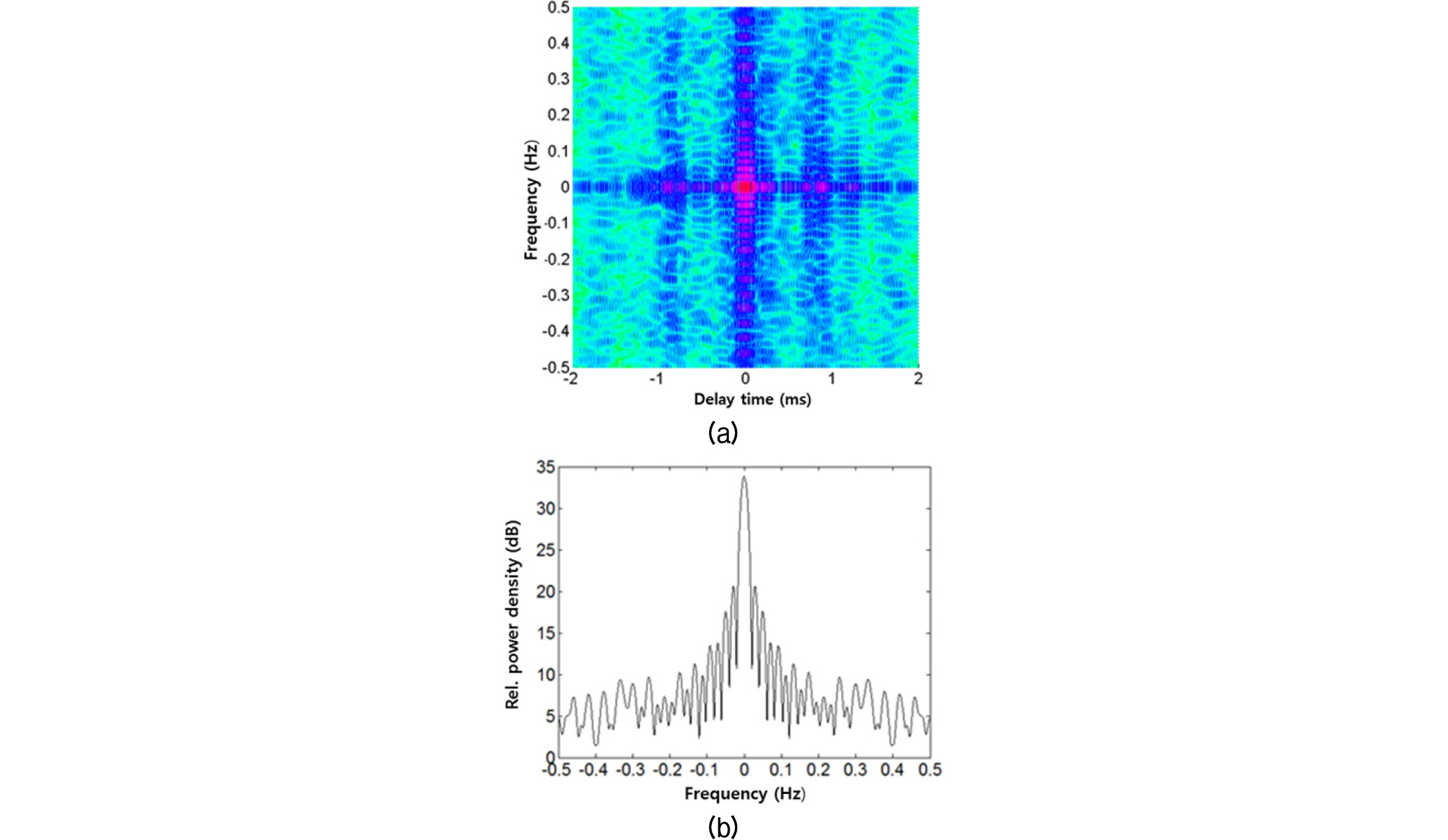
Figs. 14와 15는 Eqs. (13)과 (14)를 적용한 거리 300 m와 600 m의 채널 산란함수와 도플러확산 스펙트럼이다. 각각의 채널 산란함수에서 해면 산란이 있는 해면 반사파의 확산이 상대적으로 크게 관측된다. 직접파의 시변은 없을 것으로 예상하였으나 확산 성분이 크게 관측된다.

Fig. 14.

Channel scattering function and Doppler power spectrum at 300 m source-to-receiver range: (a) channel scattering function, (b) Doppler power spectrum.

Fig. 15.

Channel scattering function and Doppler power spectrum at 600 m source-to-receiver range: (a) channel scattering function, (b) Doppler power spectrum.

임펄스 응답의 측정 주기 T = 1로 샘플링 주파수가 1 s이므로 채널 산란 함수 분석 주파수 범위는 0.5 Hz 이다.

5.3 도플러 확산 스펙트럼과 상관시간

300 m와 600 m 에 대한 Figs. 13(b)와 14(b) 도플러 주파수 확산에 Eq. (17)을 적용하면 각각의 주파수 확산 유효치 ${\lambda }_{eff}$는 각각 0.153 Hz와 0.136 Hz이다. Eq. (18)을 적용하면 각각의 상관 시간은 약 2.76 s와 3.11 s이다.

5.4 상관 대역폭

5.4.1 지연 확산 시간 영역 특성과 상관 대역폭

Figs. 10과 11의 300 m와 600 m의 지연 확산 $\hat{I}\left(\tau \right)$에 Eqs. (21)과 (22)를 적용하여 상관 대역폭을 구하였다. 300 m의 경우 Eqs. (21)과 (22)의 결과는 각각 670 Hz와 67 Hz이고 600 m의 경우 각각 770 Hz와 77 Hz이다.

5.4.2 지연 확산 주파수 영역 특성과 상관 대역폭

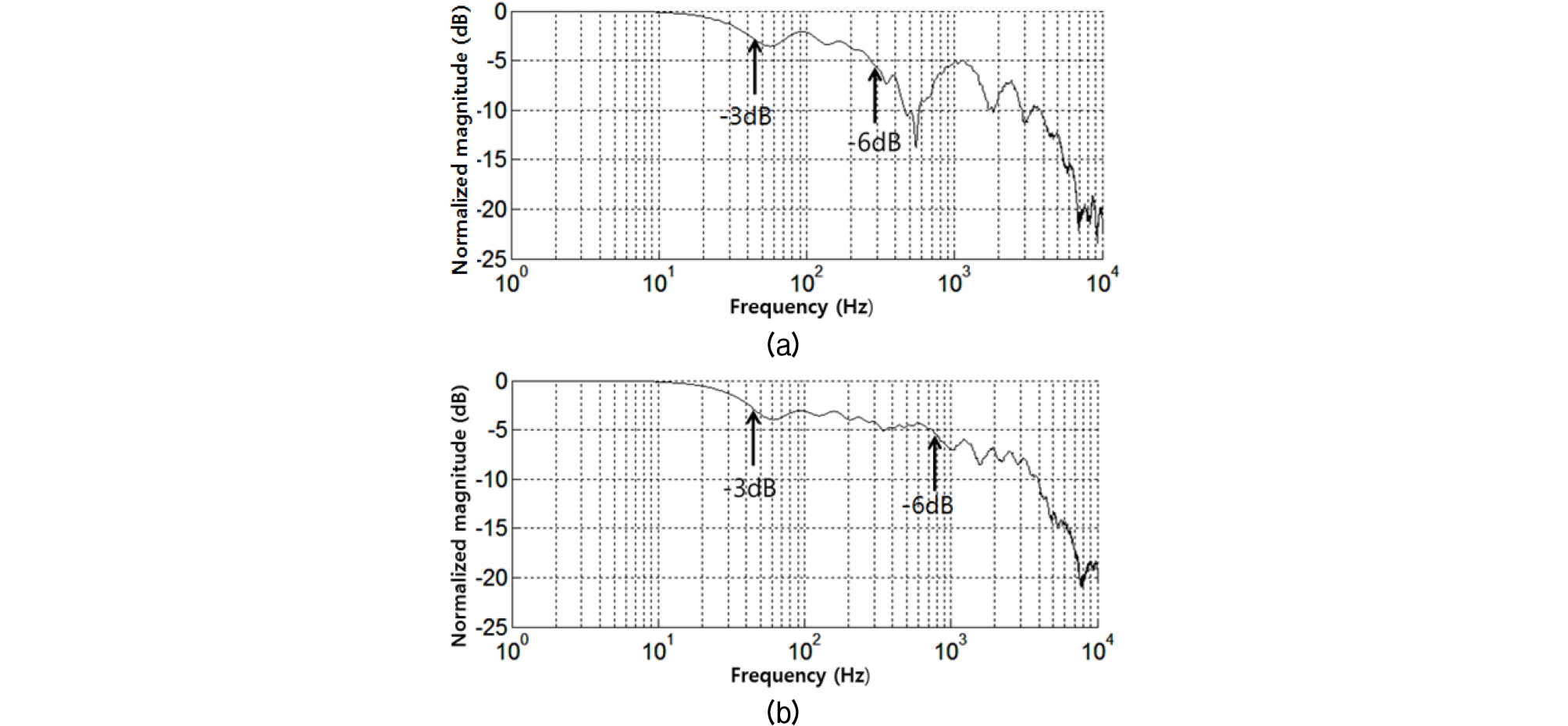
Fig. 16은 Eq. (23)을 적용한 300 m와 600 m의 채널의 주파수 상관 함수 $B\left(\Delta f\right)$이다.

Fig. 16.

Channel coherence bandwidth using LFM (from the top): (a) 300 m and (b) 600 m source- to-receiver range.

300 m의 -6 dB 대역폭과 -3 dB은 각각 약 600 Hz와 80 Hz이고 600 m의 경우 1400 Hz와 80 Hz이다.

5.4.1절의 시간 영역에서 구한 상관 대역폭과 비교하면 Eq. (21)은 주파수 상관 함수 $B\left(\Delta f\right)$의 -6 dB 기준의 상관 대역폭, Eq. (22)은 -3 dB 기준의 상관 대역폭과 유사한 결과라 판단된다.

5.5 상쇄 간섭과 보강 간섭

2.1절에서 기술한 바와 같이 동일한 다중경로 지연에서도 반송 주파수에 따라 해면 반사 경로와 해저 반사 경로의 위상 $2\pi f{\tau }_s$와 $2\pi f{\tau }_b$가 변하므로 시 불변 코히어런트 신호의 크기 $\left|P_{coh}\right|$와 위상 ${\theta }_{coh}$는 주파수에 따라 변하여 상쇄 간섭 및 보강 간섭을 갖는 주파수가 관측된다.

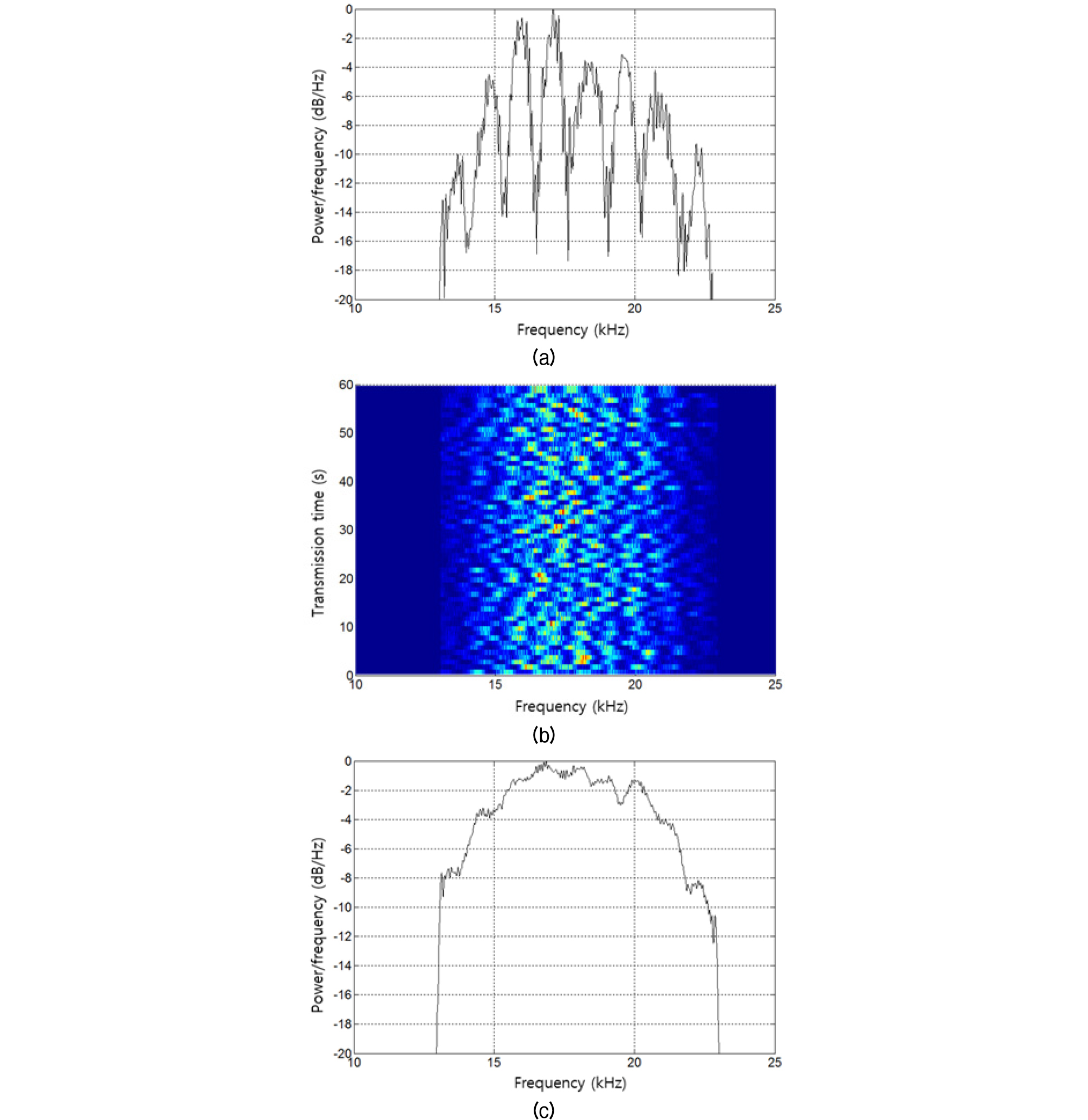
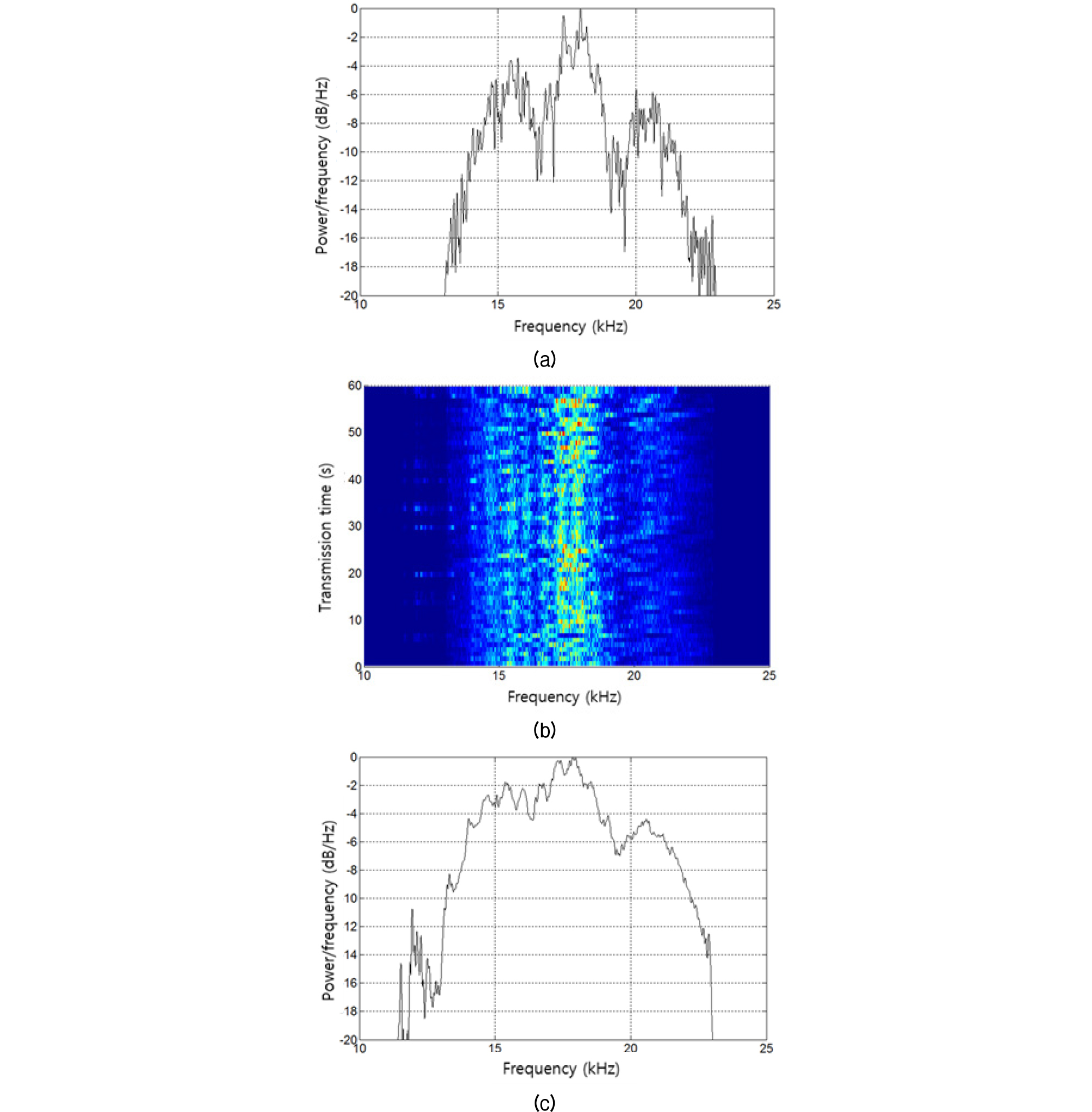
Figs. 17과 18은 각각 300 m와 600 m의 LFM 수신 신호의 스펙트럼이다.

Fig. 17.

LFM signal spectrum at 300 m source-to- receiver range: (a) spectrum of a single LFM signal, (b) spectra of 60 LFM signals versus transmission time, and (c) averaged spectrum of 60 LFM signals.

Fig. 18.

LFM signal spectrum at 600 m source-to- receiver range: (a) spectrum of a single LFM signal, (b) spectra of 60 LFM signals versus transmission time, and (c) averaged spectrum of 60 LFM signals.

Figs. 17(a)와 18(a)에서 보는 바와 같이 상쇄 간섭 및 보강 간섭을 보인다. 따라서 반송 주파수가 상쇄간섭 주파수가 되면 상관 대역폭이 심벌율보다 큰 주파수 비 선택적 페이딩 조건에서도 신호 대 잡음비가 작아질 것이다. Figs. 17(b)와 18(b)는 단위 전송 신호의 전송시간에 따른 상쇄 간섭 및 보강 간섭의 시변 특성이다. 해면 입사각이 상대적으로 큰 300 m는 해면 거칠기가 커지게 되어 해면 반사파의 시변이 상대적으로 크게 관측된다. Figs. 17(c)와 18(c)는 60개 수신 신호의 평균 스펙트럼으로 600 m에 비해 300 m 거리의 간섭 패턴은 시변 영향으로 상대적으로 뚜렷하게 관측되지는 않는다.

5.6 진폭 포락 페이딩의 통계적 분포 함수

60 s의 PN 수신 신호에 Eqs. (5) ~ (9)를 적용하여 시간 영역 페이딩의 통계적 분포 함수를 구하였다. 5.4.2절에서 구한 -3 dB 기준의 상관 대역폭 약 80 Hz를 진폭 포락 페이딩 해석의 기준 대역으로 설정하였다.

5.6.1 거리에 따른 분포 함수

Figs. 19과 20은 송수신기 거리 300 m와 600 m에 대한 페이딩 분포함수이다.

Fig. 19.

Receiver signals and fading statistics of 80 Hz bandwidth in 300 m source-to-receiver range: (a) receiver signal of 0 s ~ 10 s, $\left|P\right(t\left)\right|$ and low pass filtered $\left|P\right(t\left)\right|$ (from the top) and (b) fading statistics.

Fig. 20.

Receiver signals and fading statistics of 80 Hz bandwidth in 600 m source-to-receiver range: (a) receiver signal of 0 s ~ 10 s, $\left|P\right(t\left)\right|$ and low pass filtered $\left|P\right(t\left)\right|$ (from the top) and (b) fading statistics.

중심 주파수는 18 kHz로 하고 분석 대역은 상관 대역폭 80 Hz이다. 진폭 포락 $\left|P\right(t\left)\right|$는 분석 대역으로 필터링한 PN 신호의 힐버트 변환으로 해면 산란에 의한 시간 영역 페이딩을 추출하기 위해 힐버트 변환한 $\left|P\right(t\left)\right|$신호를 해면 우세파의 주파수로 저역 통과한 후 해면 산란에 의한 시간 영역 페이딩의 통계적 분포 함수를 구하였다. 해면 우세파의 주파수는 실험 당시 해면파 주파수의 2배인 0.5 Hz로 하였다.

거리 300 m의 Fig. 19에서 보는 바와 같이 Rice 인수 K = 2의 Rice 분포이며 시간 영역 페이딩은 해면 거칠기 주파수에 동조함을 보인다.

600 m 거리의 Fig. 20의 결과는 Rice 인수 K = 6의 Rice 분포로 해면 산란의 영향이 300 m에 비해 상대적으로 작아 K가 커진다. 해면 거칠기 주파수에 동조하는 포락선의 파형은 300 m보다 낮은 주파수를 보이는데 이는 약 2시간 이후에 행한 600 m 실험 당시에 풍속 증가로 인한 해면 파도 주파수가 낮아진 결과이다.

채널 페이딩의 통계적 분포 함수 추정에 적용한 PN 신호의 전체 길이는 60 s로 300 m 실험 당시의 해면파의 주기 4 s와 비교하면 15배에 불과하여 통계적 표본 길이는 절대적으로 부족하다. 이러한 이유로 이론적인 분포와 비교하면 편차가 크게 나타난다.

5.6.2 주파수에 따른 분포 함수

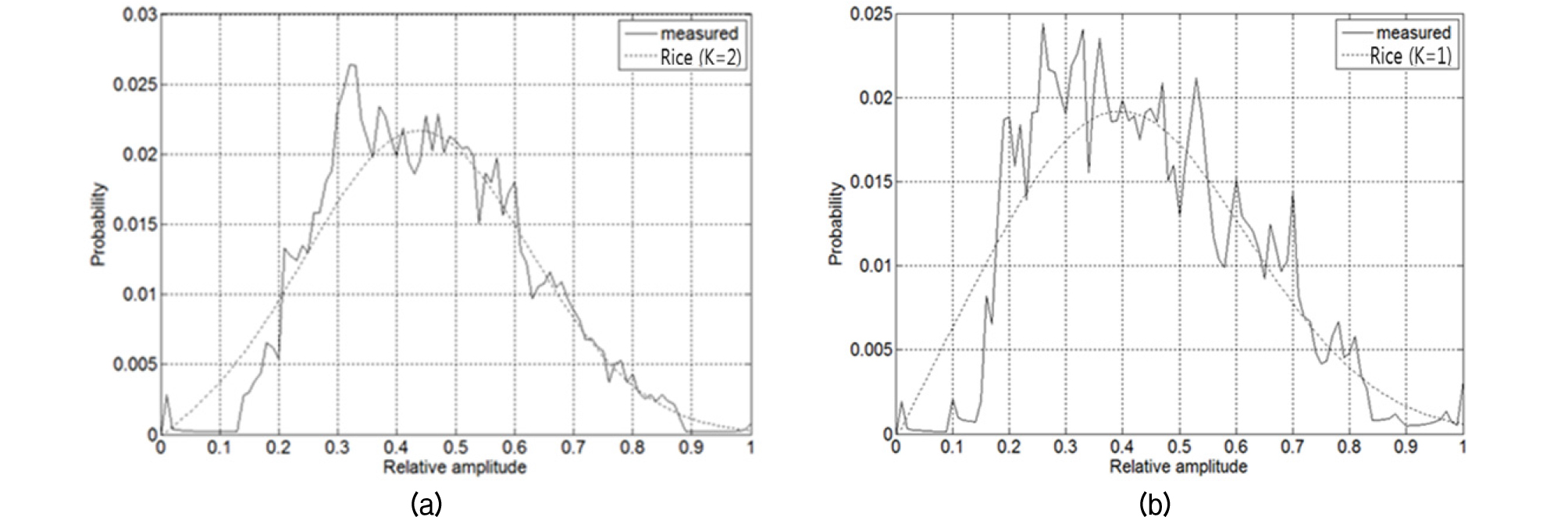
다중경로의 보강 간섭과 상쇄 간섭은 주파수에 좌우된다. 보강 간섭일 경우 2.1절에서 기술한 바와 같이 시 불변 코히어런트 성분이 커져 Rice 인수 K가 커진다. Fig. 21은 송수신기 거리가 300 m인 경우 보강 간섭을 보이는 18.0 kHz와 상쇄 간섭을 보이는 16.2 kHz의 페이딩 분포 특성으로 각각 Rice 인수 K가 2와 1로 예상한 바와 같이 상쇄 간섭 주파수에서 K가 작아진다.

Fig. 21.

Dependency of Rice factor K on constructive and destructive frequencies at source-to-receiver range 300 m: (a) constructive frequency 18.0 kHz, and (b) destructive frequency 16.2 kHz.

5.7 결과 요약 및 고찰

수심 50 m, 사니질 저질, 유효 파고 0.5 m 및 해면파 우세 주파수 0.25 Hz를 갖는 천해 환경에서 송수신기의 거리가 300 m와 600 m인 음향 채널의 채널 매개변수 특징은 Table 3와 같다. 채널 매개변수의 특징과 이들이 모뎀과 채널 코딩에 미치는 영향은 다음과 같다.

Table 3. Shallow water acoustic channel parameters in two different fixed source-to-receiver range.

최대 크기를 보이는 직접파보다 약 20 dB 낮은 다중경로를 고려하지 않을 경우 300 m와 600 m의 우세한 다중경로는 전자는 2개(직접파와 해면 반사파)이며 최대 지연 확산은 약 0.9 ms, 후자는 3개(직접파, 해면 반사파 및 해저 반사파)이며 최대 지연 확산은 약 1.6 ms이다. 600 m의 경우 해저 입사각이 작아져 해저 반사파가 추가되며 해면 반사파는 시변으로 관측된다. 300 m와 600 m의 지연 확산 유효치는 각각 약 0.3 ms와 0.26 ms로 상관 대역폭을 결정하는 이격 주파수의 상관 계수를 0.9로 하는 경우 상관 대역폭은 각각 67 Hz와 77 Hz이며 주파수 상관 함수에서 약 -3 dB의 상관 대역폭에 상당한다.

최대 지연 확산은 심벌율이 상관 대역폭 보다 큰 경우 인접 심벌간의 간섭 ISI(Iinter-Symbol Interference)을 제거하기 위한 등화기 탭 수, 확산 스펙트럼 방식의 칩 시간이나 Rake 수신기의 설계 기초 자료가 된다.

상관 대역폭은 모뎀의 심벌율과 OFDM(Orthogonal Frequency Division Multiplexing)의 부대역 기준이다.

다중경로의 보상간섭과 상쇄간섭으로 뚜렷한 간섭 페이딩 주파수가 존재한다. 따라서 상관 대역폭보다 낮은 심벌율로 전송하더라도 반송 주파수가 상쇄 간섭 주파수와 일치하면 신호대 잡음비가 낮아져 오류율이 커지게 된다. 주파수 확산 기법이 요구되는 결과이다.

300 m와 600 m의 도플러 주파수 확산 유효치는 각각 0.153 Hz와 0.136 Hz로 각각의 상관시간은 2.76 s와 3.11 s이다. 단위 전송 프레임의 시간이나 단위 심벌 시간의 기준이다.

해면 산란에 의한 시변 진폭 포락에 대한 통계적인 특성은 Rice 분포이며 상관 대역폭 이내에서 300 m와 600 m의 Rice 인수 K는 각각 2와 6으로 600 m의 경우 해면 거칠기가 작아져 K가 크다. 아울러 코히어런트 성분이 작아지는 상쇄 간섭 주파수에서는 K가 작아진다. 시변 진폭 포락은 시간에 따른 신호대 잡음비의 시변을 야기하므로 시간 확산 기법인 인터리빙 오류정정코드가 요구된다. 시변 진폭 포락은 해면파의 시변에 동조한다.

VI. 결 론

본 연구에서는 천해 환경에서 송수신기의 거리가 300 m와 600 m로 고정된 음향 채널에서 국소 채널 페이딩을 결정하는 임펄스 응답, 산란함수, 도플러 확산, 상관 대역폭, 주파수 선택적 페이딩, 상관 시간 및 시변 진폭 포락 페이딩의 통계적 분포 함수 등의 채널 매개변수들을 해석하고 이들이 모뎀이나 채널 코딩에 미치는 영향을 기술하였다.

채널의 시변 요인으로는 해변 산란파를 가정하고 페이저 기반의 다중 경로 채널 모델을 제시하였다. 아울러 해면 산란에 대한 채널 모델 모의실험 결과를 제시하였다.

페이저 기반의 채널 모델에서 제시하는 우세한 다중경로에 의한 채널 산란 함수, 주파수 선택적 페이딩과 진폭 포락 페이딩의 통계적 분포 함수에 대한 해상 실험 결과는 제안한 채널 모델이 채널 매개변수들의 측정이나 분석에 적용 가능함을 보였고 채널 매개변수들은 해면 산란의 시변에 동조하여 변하는 특징을 보였다.

Table 3에서 보는 바와 같이 천해 해양 음향 환경에서 채널 매개변수들은 직접파, 산란 성분을 갖는 해면 반사파 및 해저 반사파로 구성되는 3개 다중 경로에 의해 그 특징이 결정되고 이들 매개변수들의 주파수 및 시간 영역 페이딩은 수중음향 통신 시스템의 모뎀이나 채널 코딩이 주파수와 시간 영역에서 확산 기법을 적용해야함을 보인다.

다양한 음향 환경에 대응하는 모뎀이나 채널 코딩을 설계하기 위해서는 거울 해면에서 송수신기 상대거리 변화에 의한 채널 산란 함수, 심해 굴절파 혹은 내부파에 의한 다중 경로 지연 확산 등의 연구와 이들 개별 환경이 결합된 환경의 채널 페이딩 연구가 요구된다.

Fig. 5에서 보는 바와 같이 임펄스 응답 측정치의 정확도는 시험 신호의 특징에 좌우된다. 아울러 시험 신호의 단위 길이는 채널의 상관 시간 보다 짧아야 하며 다중 경로 지연 확산을 해석하기 위해서는 다중 경로 최대 지연 확산 시간 보다 긴 휴지기가 부가되어야 하며 시변 산란 함수를 평가하기 위해서는 가능한 빠른 주기로 단위 시험 신호를 전송해야 하므로 실 해역 실험 이전에 시험 신호의 선정과 평가가 선행되어야 할 것이다.

본 연구에서 제시하는 천해 고정 시스템의 페이저 기반 채널 모델 및 채널 매개변수들의 측정과 해석 방법은 수중통신 시스템 설계와 성능평가에 대한 기초자료가 될 것이다.