I. 서 론

로켓 발사 시 발생하는 고온, 초음속 유동은 고강도 소음원을 생성한다. 발생된 소음은 전파하여 탑재된 위성 또는 발사체 내부의 전장품에 고강도 음향하중으로 작용하여 최악의 경우 발사 임무 실패를 유발한다. 또한 로켓 소음, 넓은 의미에서 초음속 제트 소음의 크기는 인간의 청력 한계를 상회하기 때문에 관련 종사자들의 영구적 청력 손상의 주요 원인으로 보고되고 있다.^[1] 이러한 이유로 제트소음의 모델링, 예측 및 저감 기법 개발과 같은 기초연구가 국내외에서 활발히 진행되고 있다.

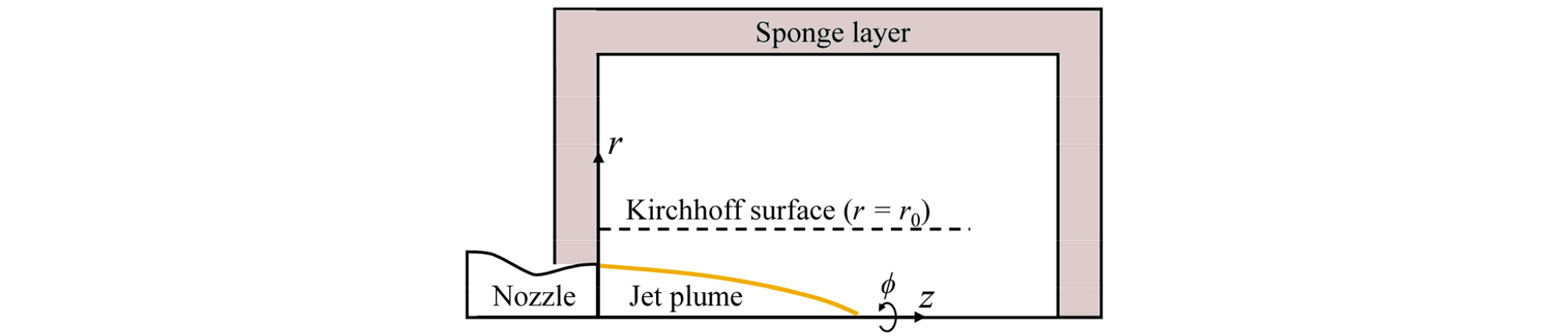
제트소음의 예측은 대표적으로 NASA SP-8072^[2]와 같은 준실험식 기반의 방법과, 전산유체해석과 같은 수치적 방법이 존재한다. 수치적 방법의 경우 초음속 유동 및 음향전파 모사를 대와류모사(Large Eddy Simulation, 이하 LES)와 같은 3차원 비정상 유동해석모델을 사용하면 수개월 이상의 긴 해석 시간이 소요된다. 이에 계산 효율이 뛰어난 음향전파 해석과 유동해석을 결합한 소음 예측기법이 개발되었다. 유동장 영역(초음속 플룸 및 인접 영역)과 그 외의 음향장 영역(파동 방정식으로 기술 가능한 영역)을 구분하여, 두 장의 경계면의 해석결과를 음향학적 수송 기법으로 원거리장 소음을 계산하는 방법이다.^[3] 만약, 수송 기법 중 하나인 Helmholtz-Kirchhoff 적분식(이하 HK 적분식)을 사용할 경우 Fig. 1과 같이 유동장과 음향장을 구분 짓는 가상의 경계면(Kirchhoff surface, 이하 K 표면)에서 유동해석으로 구한 압력(유동이 미미한 지역이므로 음압에 해당)을 적분식에 대입하여 원거리장 소음을 예측할 수 있다.^[3,4,5] 최근 일본 우주항공연구개발기구(JAXA)에서 수행된 NAL-735 모터의 원거리장 소음 예측 및 축소 모형 실험과의 상사성 연구가 이에 해당한다.^[5,6]

Fig. 1.

(Color available online) Schematic design of computational domain for supersonic jet noise and Kirchhoff surface.

초음속 유동해석 시 계산영역은 유한하기 때문에, 생성된 음파가 계산 경계면에서 반사되지 않도록 경계조건의 설정은 필수적이다. 주로 특성치 경계 조건(characteristic boundary condition)이 사용된다.^[4,7] 하지만, 경계면으로의 입사각이 클수록 성능이 저하되며 유동이 존재할 경우에는 음향 임피던스의 부정합(계산영역과 경계면 사이의)으로 인해 반사파 아티팩트가 발생한다. 이를 보완하기 위해 추가적으로 흡수층(sponge layer) 기법이 주로 사용된다.^[4,8,9] 흡수층은 Fig. 1과 같이 경계면 인근 영역에 인위적으로 감쇠 메커니즘을 추가하는 기법으로, 투과하는 음파 성분이 감쇠되어 결과적으로 무반사 조건을 모사한다. 흡수층은 수치적 안정성 측면에서 우수한 장점이 있다. 하지만, 충분한 감쇠성능을 위해서는 두께가 확보되어야 하므로 계산영역의 증가를 야기하며, 기존해석 자료 또는 초도해석으로 흡수층의 두께, 감쇠크기와 같은 파라미터의 최적화가 선행되어야 한다.^[9] 또한, 지배방정식에 감쇠식을 임의로 추가하기 때문에 사용자 설정에 제약이 있는 상용 해석 소프트웨어의 경우에는 일반적으로 적용이 불가능하다.

본 논문에서는 제트소음 해석의 계산 효율을 증대시키기 위해, 흡수층을 배제한 유동해석 결과에서 K 표면 밖의 음향장에 존재하는 반사파 아티팩트를 두 개의 마이크로폰 기법을 적용하여 제거하는 방법에 대해 논한다. 음향해석 기법으로는 Fig. 1과 같이 플룸을 감싸는 K 표면의 유동해석 결과(압력)로 원거리 소음을 예측하는 HK 적분식을 사용한다고 가정한다. 즉, K 표면에서의 초음속 유동해석 결과(흡수층 미적용)에서 관찰되는 반사파 아티팩트(이하 반사파)를 제거하였다.

II. 반사파 제거 기법

2.1 두 개의 마이크로폰 기법

본 논문에서 제안하는 반사파 제거 기법은 두 개의 마이크로폰 기법에 기반 하므로 이에 대해 간략히 기술하겠다. 도파관과 같이 단순한 1차원 음향 전파를 가정할 경우 음압 성분은 다음과 같이 기술된다.

우변의 첫 번째 항은 $-x$, 두 번째 항은 $+x$ 방향의 음압 성분을 의미하며, $A$와 $B$는 각 성분의 크기인 계수, $k$는 파수이다. 서로 다른 두 지점의 마이크로폰 신호, 즉, 음압 $p\left(x_0\right)$와 $p\left(x_1\right)$을 알 경우 두 식의 연립으로 각 방향 성분을 분리할 수 있다.

2.2 Kirchhoff 표면의 반사파 아티팩트 제거

Fig. 1에 도시한 원통형 K 표면에 두 개의 마이크로폰 기법을 적용하여 반사파 아티팩트를 제거하는 방법에 대해 기술한다. 이론적으로는 K 표면 형태의 제약은 없지만, 원통형 같이 단순한 형상일수록 계산 편의성을 확보할 수 있다. 원통좌표계를 도입하면 3차원 음향 전파는 다음과 같이 기술할 수 있다.

$H_m^{\left(1\right)}$과 $H_m^{\left(2\right)}$은 반경방향 $r$에 대하여 각각 수렴파(converging wave, $-r$ 방향)와 발산파(diverging wave, $r$ 방향)를 구성하는 제 1, 2종 Hankel 함수, $m$은 방위각 $\varphi$에 대한 음향모드의 차수, $z$는 축방향 좌표를 의미한다. $k_r$과 $k_z$는 반경방향 및 축방향 파수이며, 식 $k_r^2={\omega }^2/c_0^2-k_z^2$ 를 만족한다. Eq. (2)를 주파수영역에서 수렴파와 발산파의 선형중첩으로 기술하면 다음과 같다.^[10]

where ${\hat{\tilde{p}}}_m(r,k_z)=A_m{H}_m^{\left(1\right)}\left(k_{r}r\right)+B_m{H}_m^{\left(2\right)}\left(k_{r}r\right)$.

$\tilde{p}$는 음압 $p$의 시간영역에 대한 푸리에 변환을 의미하며, 피적분식 $\hat{\tilde{p}}$는 2차원 좌표계 ($z,\varphi$)에 대한 k-space인 ($k_z,m$)좌표계에서의 음압을 의미한다. 계수 $A_m$과 $B_m$은 각각 수렴파와 발산파의 크기를 나타내는 계수이다. 수렴파를 기술하는 $A_m{H}_m^{\left(1\right)}\left(k_{r}r\right)$항이 유동해석 결과에서 제거되어야 할 반사파 아티팩트에 해당하므로, 두 원통($r=r_0,r_1$)에서의 음압 $\hat{\tilde{p}}\left(r_0\right)$와 $\hat{\tilde{p}}\left(r_1\right)$의 연립으로 계수 $A_m$을 구하여 제거할 수 있다. 실제 측정 실험과 같이 마이크로폰을 사용하는 경우에는 두 지점의 음압을 사용하는 것이 일반적이다. 하지만, 본 연구에서는 유동해석 결과를 사용하기 때문에, $\hat{\tilde{p}}\left(r_1\right)$ 대신 다음 식과 같이 $r=r_0$에서 음압의 반경방향 차분 값을 사용하여도 동일한 결과를 얻을 수 있다.

반사파 제거 기법의 과정을 요약하면 다음과 같다.

1. 복합 파형의 획득: 흡수층을 고려하지 않은 유동해석 결과로부터 K 표면($r=r_0$)의 음압($p$)과 반경방향 차분($\partial p/\partial r$) 데이터를 추출

2. 발산파 및 수렴파 분리: 시간 및 공간에 대해 푸리에 변환하여 얻은 ${\hat{\tilde{p}}}_m$, $\partial {\hat{\tilde{p}}}_m/\partial r$ 두 데이터를 연립하여 $A_m$과 $B_m$ 을 계산

3. 반사파 제거: Eq. (3)에서 $A_m$을 대입한 뒤 역 푸리에 변환하여 반사파 성분이 제거된 음압을 최종적으로 도출

반사파 제거 코드 구성은 수치계산 소프트웨어인 MATLAB을 이용하였다. 단순한 푸리에 변환 연산이기 때문에 수분 이내로 계산이 완료된다.

III. 기법의 검증 및 적용

3.1 기법의 수치적 검증

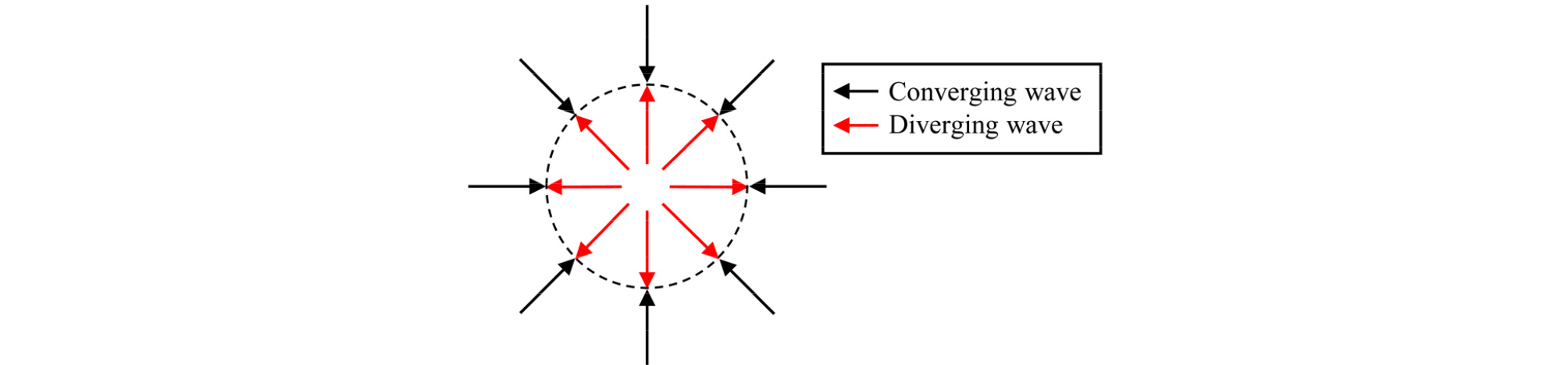
유동해석 결과에 적용하기 전, 반사파 제거 기법의 수치적 검증을 위한 과정으로써 Fig. 2와 같이 축대칭이고 원통형 발산파와 수렴파가 동일한 크기를 갖는 단순한 문제를 고려하였다. 이 경우, 반지름 r인 표면에서의 복합 파형은 다음과 같이 해석적으로 기술된다.

두 파형의 크기는 동일하게 $A$로 설정하였다.

Fig. 2.

(Color available online) Compound acoustic field for a numerical verification.

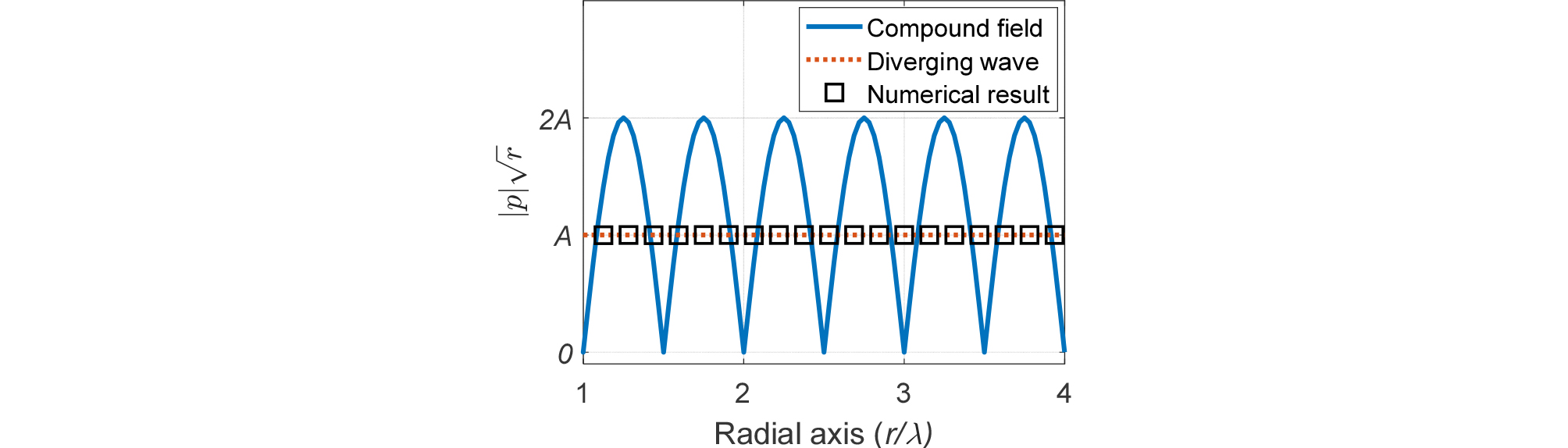
Fig. 3은 파장($\lambda$)으로 무차원화한 반경방향에 따른 수렴파 분리 결과를 나타낸 것이다. 두 반대방향 성분으로 인해 상쇄 및 보강 간섭 패턴이 관찰되며, 수렴파 분리 결과와 발산파 성분[Eq. (5)의 두 번째 항]이 정확히 일치하는 것을 확인할 수 있다.

Fig. 3.

(Color available online) Calculation result of separation of incoming wave field.

3.2 초음속 유동해석 적용

3.2.1 마하수 1.8 초음속 노즐 유동해석

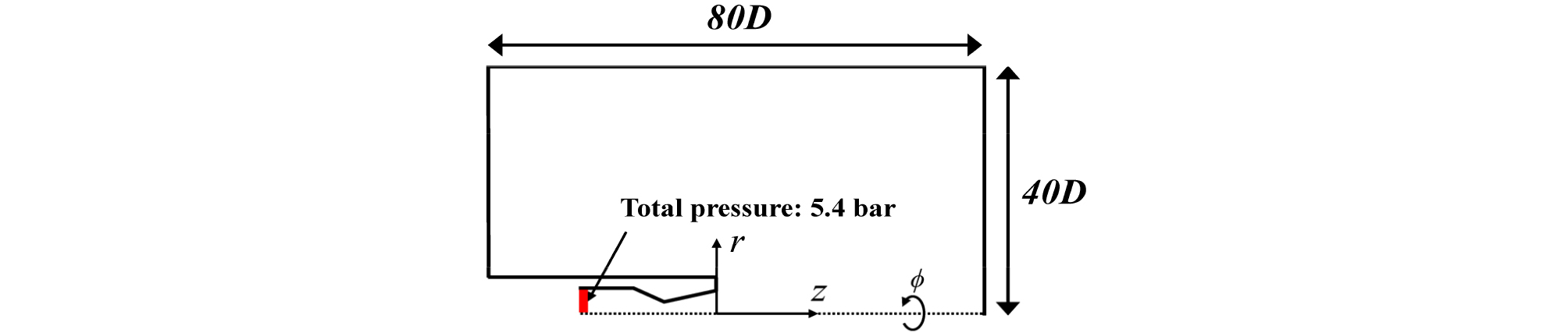
본 연구에서는 최적팽창 기준 마하수 1.8, 출구지름(D)이 20 mm인 초음속 소형 노즐을 고려하였다. 매질은 상온 1기압의 공기이며 노즐 입구에서의 전압은 5.4 bar로 선정하였다. 최적팽창 조건을 만족하는 입구 전압은 5.8 bar이기 때문에, 고려한 노즐은 과팽창 조건에 해당한다. Table 1은 노즐의 유동 조건을 정리한 것이다.

전산유체해석 기법으로는 제트소음 연구에 적용된 바 있는 Detached-Eddy Simulation(DES)을 사용하였다.^[11] DES는 노즐 벽면의 경계층과 같이 과도한 격자가 필요한 지역에서는 Reynolds averaged Navier Stokes(RANS), 그 외의 영역에서는 LES가 적용되어 단순히 LES만을 사용한 경우 대비 효율적인 해석이 가능하다는 장점이 있다. 수행한 DES 해석 조건은 Reference [12]에 자세하게 명시하였고, 본 논문에서는 반사파 제거와 관련한 주요 사항만 기술하였다. 상용 전산유체해석 소프트웨어 ANSYS FLUENT를 사용하였고, 2차 공간 차분법을 적용하였다. 플룸에서의 최대 격자 크기는 0.0018 m[스트로우홀 수(Strouhal number) 기반 최대 신뢰주파수 9.1 kHz]로써, 총 4천만 개의 격자를 구성하였다. 해석 시간 간격은 10^-6 s이고, 0.02 s 해석까지 120일이 소요되었다. Fig. 4에 유동해석을 위한 전체 계산 영역의 축대칭 단면을 도시하였다. 반사파 저감을 위한 흡수층은 적용하지 않았다.

Fig. 4.

(Color available online) DES domain for supersonic nozzle-flow analysis.

3.2.2 반사파 제거 결과

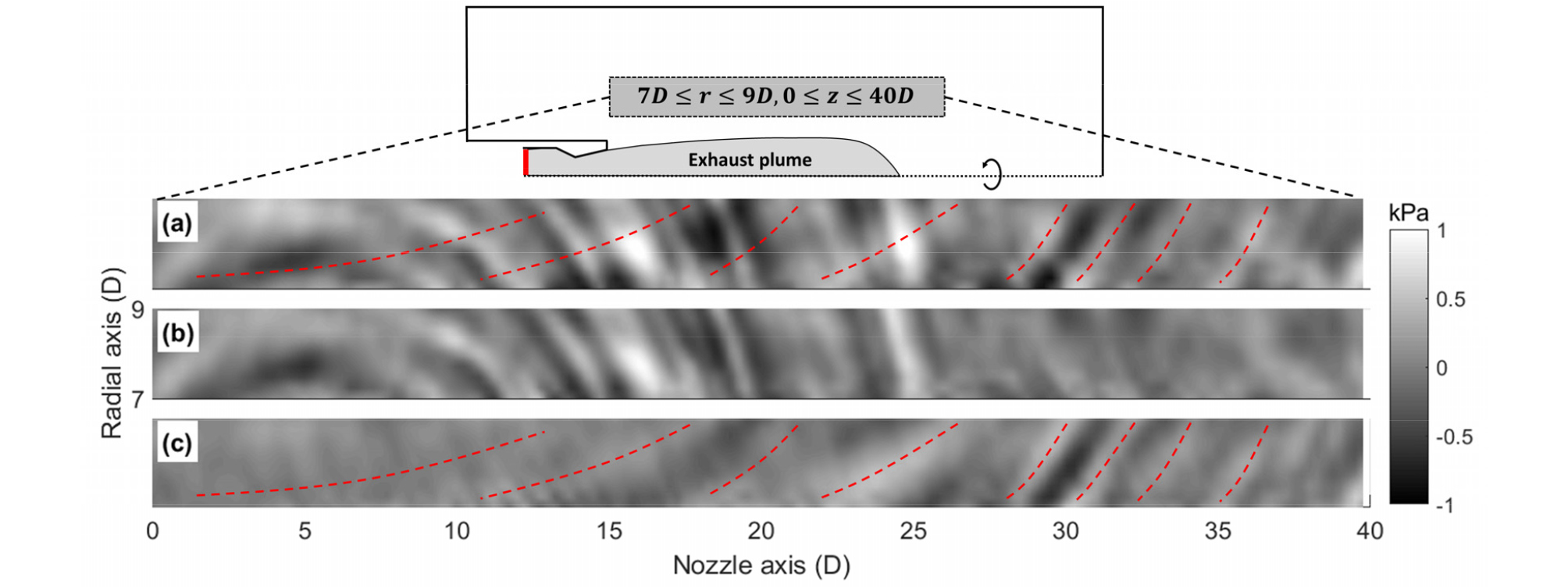
비교 연구를 위한 반사파가 제거된 유동해석 결과가 존재하지 않으므로, 발산파와 수렴파(이하 반사파) 성분을 가시화하여 제거 여부를 확인한다. 이를 위해 K 표면을 내부 벽면으로 하는 원통관($7D\le r\le 9D$, $0\le z\le 40D$ )을 설정하여 반사파 제거 기법을 적용하였다. 계산결과는 Fig. 5에 나타내었다. $t=0.013s$일 때의 축대칭 단면의 2차원 압력분포를 도시하였고, 계산 격자 간격은 $r$, $z$ 방향 모두 $0.25D$이다. 유동해석 결과인 Fig. 5(a)에서는 $z=15D$ 인근에서 주요 소음 성분이 관찰된다. 이는 제트소음 종류 중 하나인 후류 방향의 소음 지향성을 결정하는 large-scale structure의 초음속 대류에 의한 Mach wave radiation 성분으로 추정된다.^[13] 흡수층을 고려하지 않았기 때문에 ± r 방향 성분을 갖는 파면 다수가 동시에 관찰된다. 가시성을 위해 반사파($-r$ 방향)의 파면은 적색 점선으로 표시하였다. 분리 후 결과인 Fig. 5(b)에는 Mach wave radiation 성분이 온전히 유지되면서 반사파가 제거된 것을 확인할 수 있다. 반사파만 취한 결과인 Fig. 5(c)에서는 해당 성분이 뚜렷하게 관찰된다.

Fig. 5.

(Color available online) Calculation result of the separation of reflected waves from the DES result. Pressure contour $(r,z)$ when $t=0.013s$: (a) the DES result, (b) after the separation, and (c) collection of reflected waves.

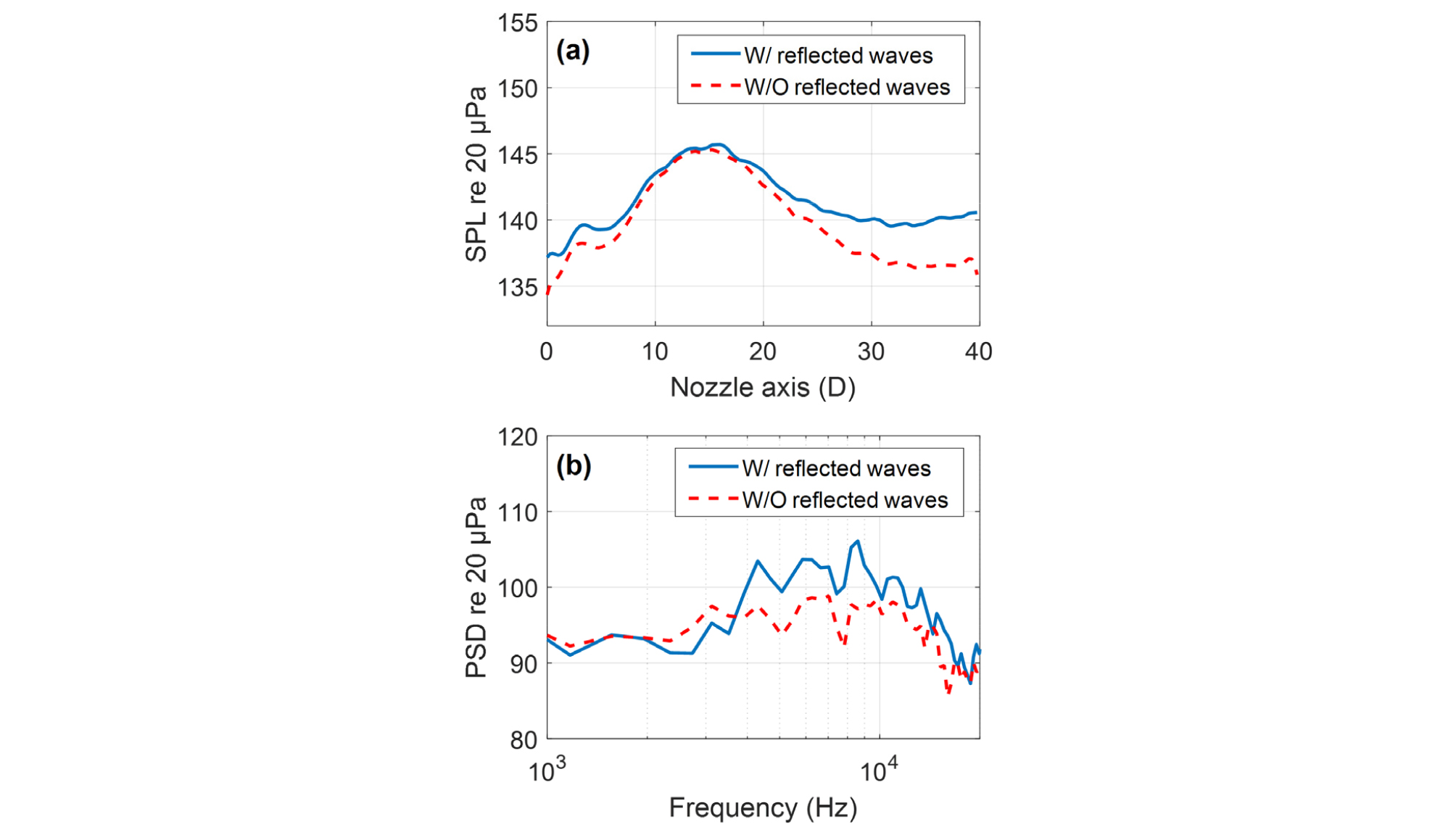
Fig. 6은 K 표면인 $r=7D$에서 분리 전과 후의 위치별 OASPL과, 전후 레벨 변화가 큰 $z=35D$에서의 스펙트럼을 비교한 것이다. 반사파가 제거되었기 때문에 Overall Sound Pressure Level(OASPL) 모두 전체적으로 감소한 것을 확인할 수 있다. 스펙트럼 또한 마찬가지로 감소하였지만, 3 kHz 대역에서는 소폭 증가하였다. 이는 진행파와 반사파의 상쇄 간섭이 없어졌기 때문으로 추측된다. 소음 크기가 작은 지역($z\le 10D$ 와 $z\ge 30D$)에서 감소폭이 더 크게 관찰되는데, 이는 Mach wave radiation 성분이 계산경계면에서 반사되어 돌아온 아티팩트가 제거되었기 때문으로 추측된다.

Fig. 6.

(Color available online) Calculation result of the separation of reflected waves from the DES result : (a) OASPL along the nozzle axis at $r=7D$ and (b) power spectral densities at $r=7D$, $z=35D$.

IV. 고찰 및 결론

두 개의 마이크로폰 기법을 초음속 제트 유동해석 결과에 적용하여 Fig. 5와 같이 반사파 아티팩트를 제거할 수 있었다. 반사파 제거 기법은 계산효율 측면에서 흡수층 대비 큰 장점을 갖는다. MATLAB 코드 기준으로 단순히 시공간 푸리에 변환 후 연립 연산이 전부이기 때문에 수 분 이내에 계산이 완료된다. 반면에 전산유체해석 단계에서 흡수층을 추가하기 위해서는 기본적으로 계산 도메인의 크기가 증가해야 한다. Mani^[9]에 따르면 흡수층의 두께($L$)는 주파수($f$)와 음속($c_0$)으로 무차원화된 스트로우홀 수($fL/c_0$) 기준으로 0.5에서 2 사이가 적절하다. Fig. 6(b)에서 관찰되는 피크 대역폭 내인 4 kHz를 기준으로 스트로우홀 수 2 를 가정한다면 Fig. 4에 도시한 계산영역의 체적은 흡수층의 추가로 인해 약 35 %, 격자수는 14 %가 증가하게 된다. 0.02 s까지 소요된 계산시간이 120일이기 때문에, 단순히 격자수 증가 기준으로 보면 최소 17일의 계산시간이 추가된다.

유동/음향해석 결합기법은 전산유체해석만을 사용할 경우 요구되는 과도한 연산량으로 인한 대안으로서 탄생한 것이다. 플룸에서 충분히 멀어지면 Navier-Stokes 방정식이 아닌 단순한 파동 방정식을 기반으로 하는 음향 수송 기법으로 소음 예측이 가능하기 때문이다.^[3,4] 본 논문에서 제안한 반사파 제거 기법도 이와 유사하다. 유동해석 단계에서 발생하는 반사파를 흡수층이 아니라, 제트 소음 예측 분야에서는 시도된 적이 없는 음향학적인 방법을 도입하여 반사파 아티팩트를 제거할 수 있었고, 예측의 정확도는 유지하면서 계산시간을 대폭 단축할 수 있었다.

반사파 제거기법은 유동해석이 완료된 뒤에 적용되기 때문에 반사파의 존재로 인한 유동해석 결과의 영향 연구가 필수적이다. 반사파 성분이 제트 플룸으로 전파하여 소음원 형성에 영향을 미칠 가능성이 있기 때문이다. 이는 향후 흡수층이 고려된 유동해석 결과와의 비교로 반사파 제거 기법의 정합성 검증연구와 함께 수행할 계획이다.