I. 서 론

해수면의 쇄파에 의해 자연적으로 발생한 기포는 자체가 해양 배경소음의 원인이 되는 동시에 수중 음전달에 영향을 미치는 주요 인자가 된다.^[1] 또한, 기포의 음향 감쇠특성을 이용하여 해양구조물 작업 시 수중 파일링 충격소음 저감,^[2] 선박소음 저감^[3] 및 지구물리탐사 시 해수면 반사 저감^[4] 등 다양한 분야에서 ‘에어버블커튼’ 개념^[5]이 활용되고 있다.

기포의 공진, 산란, 감쇠 등 음향 특성은 기포의 크기에 따라 달라지므로, 해양에서 자연적으로 존재하는 기포의 양과 크기 분포는 많은 연구의 대상이 되어왔다.^[6,7] 해양에서 기포의 분포는 직접적인 관측이 용이하지 않으므로 주로 음향계측에 의해 역으로 추정하는 역산 방식을 취해왔다.^[1,8] 초기의 역산은 기포의 공진 성분만을 고려하였으나, 음향학적으로 정확한 기포의 크기 스펙트럼을 구하기 위해서는 비공진(off-resonance) 기포의 영향까지 고려되어야 하며, 이를 위해 제 1종 Fredholm 적분방정식 형태의 역산란 문제를 풀어야 한다는 점이 지적되었다.^[9]

기포 역산란 문제를 풀기 위해 Commander와 McDonald^[10]는 기저함수로써 선형 B-스플라인과 가중 잔차 방법을 적용한 유한요소 해석법을 제안하였다. 본 기법은 크기가 작은 기포 영역까지 정밀한 역산이 가능하나, 격자수가 증가할수록 행렬의 조건수가 커져서 해가 불안정해지는 단점이 있다. Caruthers et al.^[11]은 복잡한 적분방정식을 푸는 대신에 2단계 반복법(two-step iterative method)을 제안하였고 모의 데이터와 계측 데이터에 적용하여 기포의 분포를 추정하였다. Caruthers et al.^[11]은 제안된 기법이 적분방정식의 직접적인 역산에 비해 비교적 간단히 해를 추정할 수 있으나, 해의 정밀도는 계측 데이터의 정확성에 따라 달라진다고 기술하였다.

기포 역산란과 유사한 문제로서 지음향 역산 문제를 들 수 있다. Rajan^[12]은 Born 근사를 통해 평면파의 반사계수에 대한 선형 적분 방정식을 유도하였고 해저면의 물성치(음속, 감쇠계수, 밀도)를 역산하였다. Gerstoft^[13]는 지음향 역산 문제를 최적화 문제로 정의한 후 유전 알고리즘 최적화를 통해 역산을 수행하였고 해를 확률적으로 제시하였다.

본 연구에서는 기포 역 산란 문제를 최적화 문제로 정의한 후 최적화를 통해 기포의 크기 분포를 역산하는 기법을 제시하였다. 제안된 기법을 시뮬레이션을 통해 검증하였으며, 기포 음향실험을 통해 획득된 감쇠 데이터로부터 기포의 크기 분포를 역산하였다.

본 논문의 구성은 다음과 같다. 제 II장에서는 역산이론을 기술하였고, 시뮬레이션 검증 결과를 제시하였다. 제 III장에서는 기포 실험에 관해 설명하였고 실험 및 역산 결과를 제 IV장에서 논의하였다. 끝으로 제 V장에서 요약 및 결론을 맺었다.

II. 역산 기법

2.1 역산 이론

수중에서 기포가 확률 분포함수 $n\left(a\right)$에 따른 군집을 이룰 때, 주파수 $f$에서의 매질의 평균 감쇠 계수(attenuation coefficient) $a\left(f\right)$는 다음과 같이 적분방정식으로 표현된다.^[11]

Eq. (1)에서 $k_0$는 기포가 없을 때 매질의 파수(wavenumber)를 의미하며, $n\left(a\right)da$는 단위 체적당 반지름이 $a$와 $a+da$ 사이에 속하는 기포의 개수에 해당한다. 또한 $f_r\left(a\right)$와 $\delta (a,f)$는 반지름이 $a$인 기포의 공진 주파수와 댐핑상수를 각각 나타낸다. 공진주파수는 기포의 크기에 따라 달라지며 댐핑상수는 기포의 크기와 주파수에 따라 달라진다. Clay와 Medwin^[1]이 제안한 공진 주파수와 댐핑상수의 계산 방법을 부록에 수록하였다. Eq. (1)은 제1종 Fredholm 적분방정식에 해당하며, 기포의 분포 $n\left(a\right)$를 구하는 역산문제는 대표적인 ‘ill-posed’ 문제에 해당한다.^[9,11]

최적화 기법의 적용을 위해 기포의 분포와 감쇠 계수를 이산화 한 후, 각각 벡터 $\overrightarrow{n}=[n_1,n_2,...,n_{N_a}{]}^T$ 와 $\overrightarrow{\alpha }=[a_1,{\alpha }_2,...,{\alpha }_{N_f}{]}^T$로 표현한다. 이 때, $N_f$는 주파수 영역에서 이산화 된 감쇠 계수의 수이고 $N_a$는 기포의 반지름 영역에서 이산화 된 기포의 개수를 의미한다. 또한 ${\left(A\right)}^T$는 행렬$A$의 전치행렬이다. 감쇠 계수의 계측값을 $\overrightarrow{\alpha }\text{'}$라 할 때, 기포 분포의 최적 추정값 $\hat{n}$은 다음과 같이 계측값과 모델[Eq. (1)]과의 오차 제곱합이 최소가 될 때 인자로 정의한다.

Eq. (2)와 같은 최소 제곱 문제(least square problem)의 해를 구하기 위해 다양한 알고리즘이 개발되어 왔다. 본 연구에서는 안정적으로 해를 찾을 수 있으며 비교적 빠르게 해에 수렴하는 Levenberg-Marquardt (LM) 기법^[14]을 적용하였다. LM기법의 반복 계산식은 다음과 같다.

이 때, 연산자 $diag\left(A\right)$는 행렬 $A$의 대각성분을 제외한 항이 0이 되도록 대각행렬을 구성하는 연산자이고, ${\overrightarrow{r}}^k$는 $k$번째 반복계산 단계에서의 오차, 즉 ${\overrightarrow{r}}^k=$$\overrightarrow{\alpha \text{'}}-{\overrightarrow{\alpha }}^k$이다. Jacobian 행렬$J$는 $J_{i,j}=\frac{\partial r_i^k}{\partial n_j^k}$로 정의된다. Eq. (3)에서 ${\mu }_k$는 해에 수렴하는 속도를 제어하는 인자로서 각 단계별로 그 값이 다르다. 본 연구에서는 Cui et al.^[15]이 제안한 방법을 따라 다음과 같이 정의하였다.

LM기법을 포함한 대부분의 최적화 알고리즘에서 초기해를 추정하는 것은 중요한 문제이다. 초기해의 추정이 잘못되는 경우 전역 최적해가 아닌 국소 최적해로 수렴할 우려가 있기 때문이다. Eq. (1)은 주파수 $f$에서 감쇠 현상은 해당 주파수에서 공진을 일으키는 크기의 기포뿐만 아니라 다른 크기의 기포의 영향을 모두 포함한 것이다. 그런데 (i) 주파수 별 공진 상태의 기포의 영향만을 고려하고, (ii) 기포의 표면장력을 무시하며, (iii) 댐핑상수($\delta$)는 상수라 가정할 때 Eq. (1)로부터 기포 분포는 다음과 같이 추정될 수 있다.^[1,11]

비록 여러 가정이 포함되었지만, Eq. (5)는 초기해 추정에 타당할 것으로 판단된다. Eq. (5)에 의하면 감쇠 계수의 주파수 범위 $\left[f_{\min ,}{f}_{\max }\right]$에 대응되는 기포의 공진 반지름 범위 $\left[a_{\min ,}{a}_{\max }\right]$안에서만 초기해가 정의된다. 따라서 Eq. (1)의 우항에서 적분영역은 $\left[a_{\min ,}{a}_{\max }\right]$에 국한되며, 적분영역 밖의 기포의 영향은 고려되지 않는다. 이러한 제한된 적분영역의 영향은 끝단 주파수, 즉, $f_{\min }$과 $f_{\max }$ 근처에서 크게 되며, 영향의 정도는 기포 분포함수[$n\left(a\right)$]의 형태에 따라 달라질 것이다.

한편, Eqs. (3)과 (4)의 ${\alpha }_i$[Eq. (1)의 $\alpha \left(f_i\right)$]는 수치적분을 통해 구할 수 있다. 데이터의 개수($N_a$)가 충분하지 않을 경우 수치적분의 정도를 높이기 위해 데이터 보간(interpolation)이 필요하다.

2.2 역산 시뮬레이션

역산 기법의 검증을 위해 시뮬레이션을 수행하였다. 시뮬레이션에 사용된 기포의 분포는 Caruthers et al.^[11]의 Cases I과 II의 정보를 사용하였다. 각 시뮬레이션의 기포분포는 Table 1과 같다.

시뮬레이션의 과정은 다음과 같다. 우선, Table 1의 기포분포를 이용하여 감쇠 계수를 Eq. (1)로부터 구한 후 이를 계측값(참값)으로 가정하였다. Eq. (5)로부터 초기해를 추정한 후, Eq. (3)의 반복계산을 수행하였다. 이 때, 각 단계에서 오차의 크기(${ϵ}^k=||{\overrightarrow{r}}^k||$)를 평가한 후, 오차의 크기가 ${10}^{-6}$ 보다 작거나 이전 단계 대비 오차 크기의 감소율이 1 % 이내인 경우를 수렴조건으로 설정하였다. 시뮬레이션에서 주파수의 범위는 30 kHz ~ 276 kHz이고, 데이터의 개수($N_f$)는 150이다. 또한 기포의 반지름은 14 μm ~ 128 μm의 범위에서 75개의 데이터 개수($N_a$)로 이산화 하였으며, 적분 시에는 150개의 데이터로 선형보간을 수행하였다.

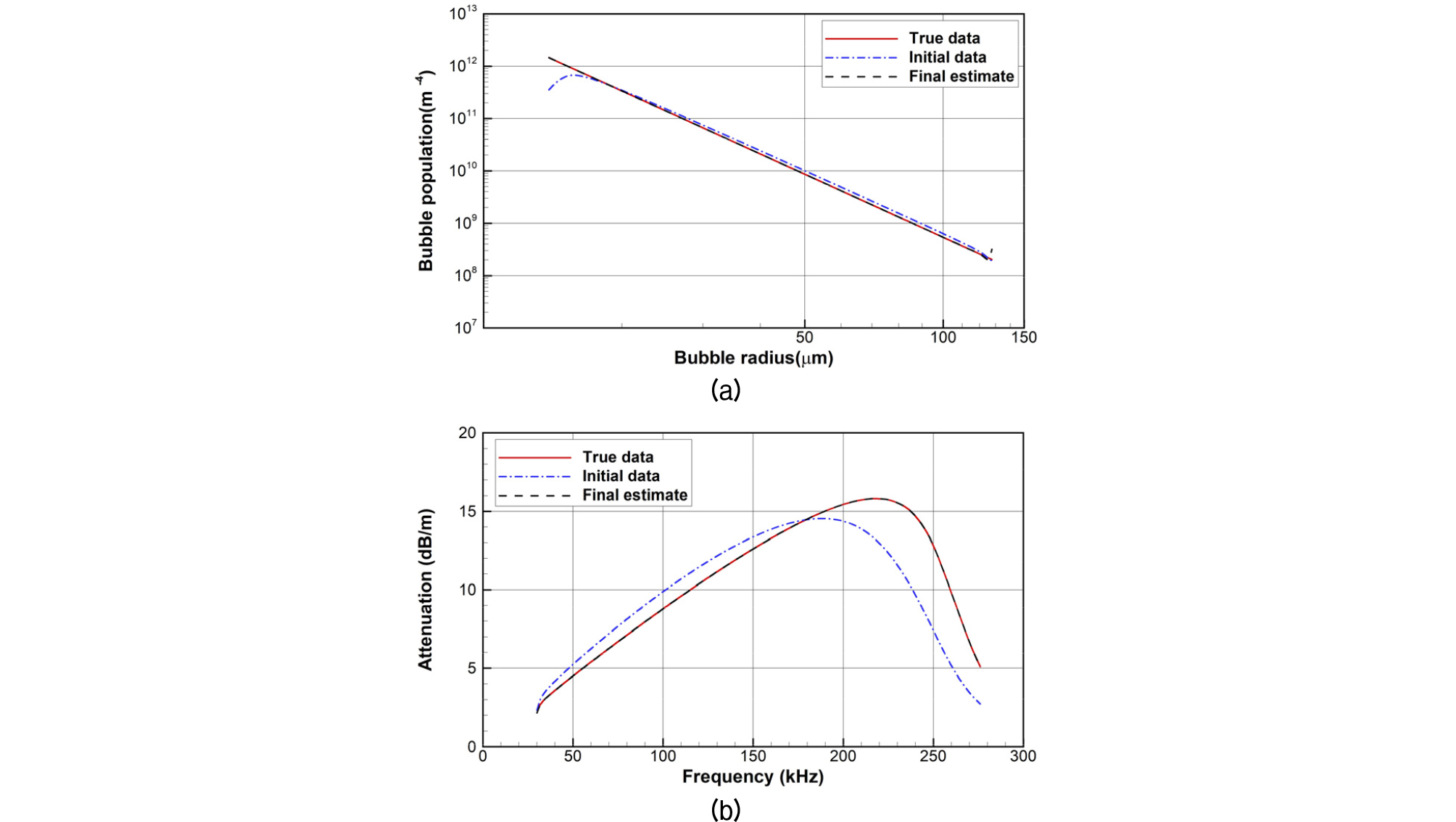
Fig. 1은 Case I의 시뮬레이션 결과를 보여준다. Fig. 1(a)에는 실제 기포분포(적색 실선), Eq. (5)에 의해 추정된 초기해(청색 일점쇄선) 그리고 최적 기포분포(흑색 점선)를 나타내었다. Fig. 1(a)의 세가지 기포분포에 대응하는 감쇠 계수는 Fig. 1(b)와 같다. Eq. (1)에서 감쇠 계수의 단위는 [nepers/m]이나 Fig. 1(b)에서는 [dB/m]의 단위로 환산되었다. 1 dB/m는 약 8.686 nepers/m에 해당한다. Fig. 1(b)에서 실제 감쇠 계수(적색 실선)와 초기해에 해당하는 감쇠 계수(청색 일점쇄선)와의 비교적 큰 차이는 비공진 기포의 포함여부, 표면장력의 고려여부, 그리고 댐핑상수의 크기 의존성 고려여부 등에 기인한다. Case I은 5회의 반복계산을 통해 수렴조건에 도달하였고, 각 계산단계에서 오차는 Table 2와 같다. Fig. 1(a)의 기포분포에서 참값(적색 실선)과 최종 추정값(흑색 점선)을 비교할 때, $a_{\max }$근처에서 근소한 차이를 제외하면 추정 정도가 매우 높음을 확인할 수 있다. 특히, 감쇠 계수의 경우는 참값과 추정값이 거의 일치하는 결과를 얻었다.

Fig. 1.

(Color available online) Simulation results for Case I: (a) bubble population density, (b) attenuation.

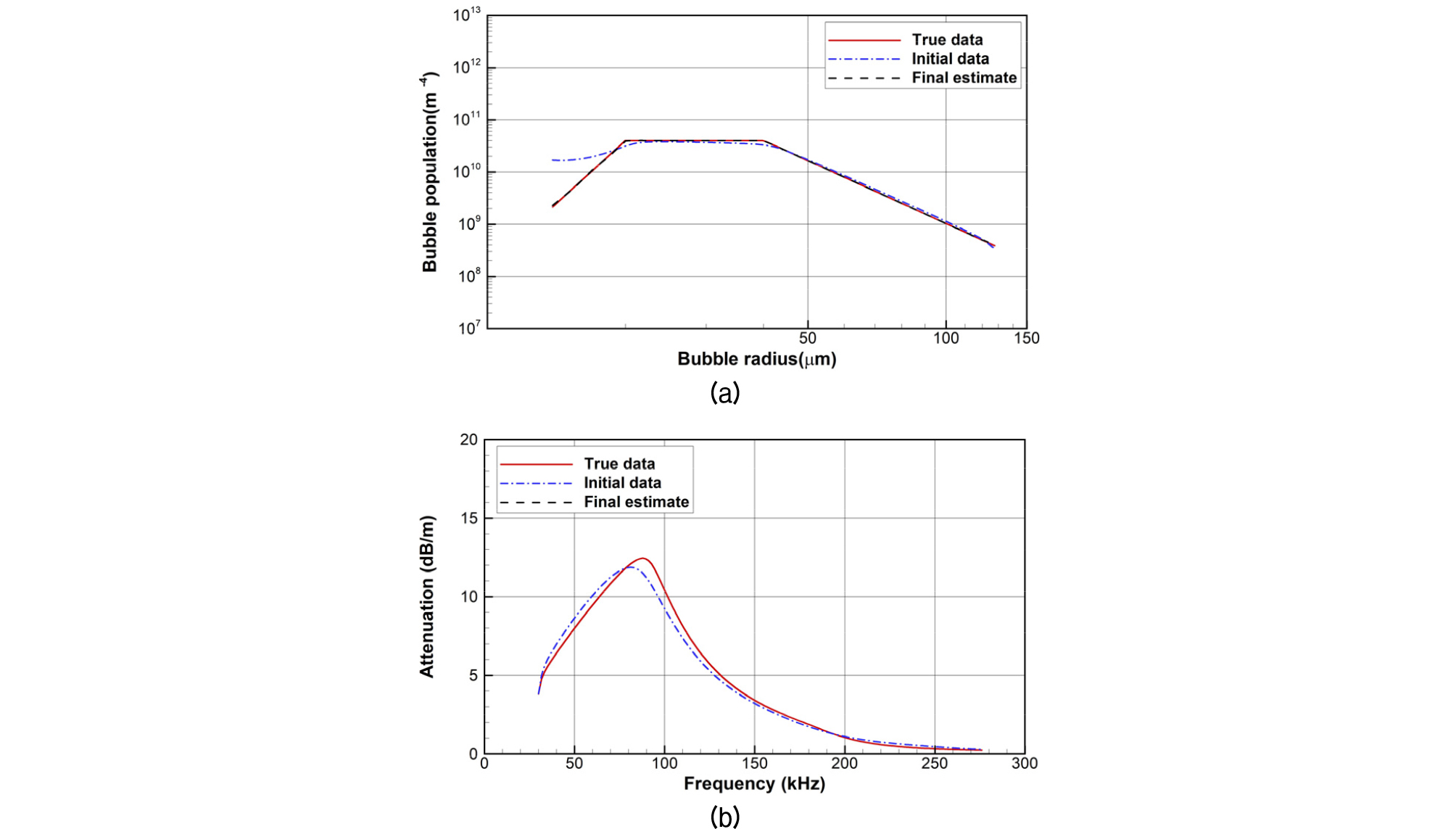
Fig. 2는 Case II의 시뮬레이션 결과를 보여준다. Fig. 2(a)에서 특히 작은 크기의 기포영역에서 초기해(청색 일점쇄선)와 참값(적색 실선)과의 큰 차이는 본 영역에서 표면장력의 영향이 특히 큰 점에 따르는 것으로 판단된다. Case II는 6회의 반복계산을 통해 수렴조건에 도달했으며, 각 계산단계에서 오차는 Table 2와 같다. Fig. 2의 결과로부터 Case I에 비해 Case II는 기포의 분포 형태가 복잡함에도 불구하고 최적화 과정을 통해 기포 분포를 잘 추정함을 확인하였다.

Fig. 2.

(Color available online) Simulation results for Case II : (a) bubble population density, (b) attenuation.

III. 기포 실험

기포 실험은 1.0 m × 0.54 m × 0.6 m(L × H × B)의 크기를 갖는 사각수조에서 수행하였으며, 기포 발생기의 종류 및 분사하는 공기 유량의 변화에 따른 음향 특성 변화를 확인하였다. 공기 공급은 외부의 에어 펌프를 사용해서 수조 내부의 기포 발생장치로 주입하였으며, 주입하는 공기의 양은 공기 유량계(TSI MODEL 4040)를 사용해서 계측하였다. 실험에 사용한 기포 발생장치는 총 3종(Fig. 3의 아래에서부터 Bubbler I, II, III)이고 각각의 기포 발생장치의 제원은 아래 Table 3과 같다.

Fig. 3.

(Color available online) Air bubble generator (bubbler I, II, III from the bottom).

기포 발생기 및 공기 유량 변화에 따른 음향 특성 변화를 확인하기에 앞서 조건별 기포의 발생 특성을 확인하기 위해 음향 계측과 별도로 3종의 기포 발생장치에서 발생하는 기포를 촬영하였다. 기포 촬영은 발생하는 기포의 크기 및 군집도를 보다 명확히 확인하기 위해 초고속 카메라(Photron FASTCAM Mini AX50)를 사용하였으며, 초당 6,000 frame으로 촬영하였다. 특히 기포 이미지 촬영 시 기포의 형태를 비교적 명확히 구분하기 위해 Fig. 4와 같이 카메라 반대편에 조명을 설치하여 발생하는 기포의 그림자를 촬영하였다.

Fig. 4.

(Color available online) Test set-up of high- speed camera experiment.

음향 실험은 영상 촬영과 별도로 진행하였다. 음원과 수중 청음기는 수조 길이 방향의 중심에 설치한 기포 발생기를 기준으로 양쪽으로 각각 100 mm, 폭 방향은 간이수조의 중심, 높이 방향은 수조 바닥으로부터 250 mm 떨어진 지점에 위치시켰으며, 음원으로는 ITC 1032, 수중청음기는 Reson TC 4033을 사용하여 계측하였다. 수중청음기의 신호는 아날로그 필터(Krohn-Hite model 3364)와 DAQ(NI PXI 6115)를 거쳐 컴퓨터에 저장되었다. 음원 신호는 주파수 1, 3, 5, 10, 20, 30, 40, 50, 60, 70, 80, 90, 그리고 100 kHz의 사인파 펄스(Continuous Waveform pulse, CW pulse)가 사용되었다. 이는 공진주파수 기준으로 38 μm에서 3.8 μm 사이 반지름의 기포에 해당한다.

본 실험구성에서 바닥면에 의한 첫 번째 반사파는 직접파의 도달 후 약 0.23 msec. 후에 도달한다. 이는 20 kHz 사인파를 기준으로 할 때, 파장의 4.5배에 해당한다. 따라서 20 kHz 이하의 주파수에서는 펄스폭은 파장의 4배가 되도록 설정 하였고, 다른 주파수에서도 펄스폭이 0.23 msec. 이내가 되도록 설정하였다. 각 주파수에서 음향 계측은 기포가 없는 경우 100회, 기포 발생 시 6,000회 반복 수행하였다.

IV. 실험 결과

4.1 영상 분석 결과

초고속 카메라로 촬영한 이미지를 사용하여 기포 특성(크기, 군집도)를 파악하기 위해 Fig. 5의 절차에 따라 별도의 해석을 수행하였다. 우선 촬영 영역(해상도)과 실제 영역 간의 크기 보정을 위해 이미지 교정 작업을 별도로 수행하였다. 보정 후 실제 이미지의 크기는 193.94 mm × 145.45 mm(L × H)이다. 이후 촬영한 이미지의 밝기와 명암을 조절하는 작업을 통해 기포의 크기 및 이미지 내 기포 개수를 추정하였다.

Fig. 5.

(Color available online) Bubble shadow image analysis process.

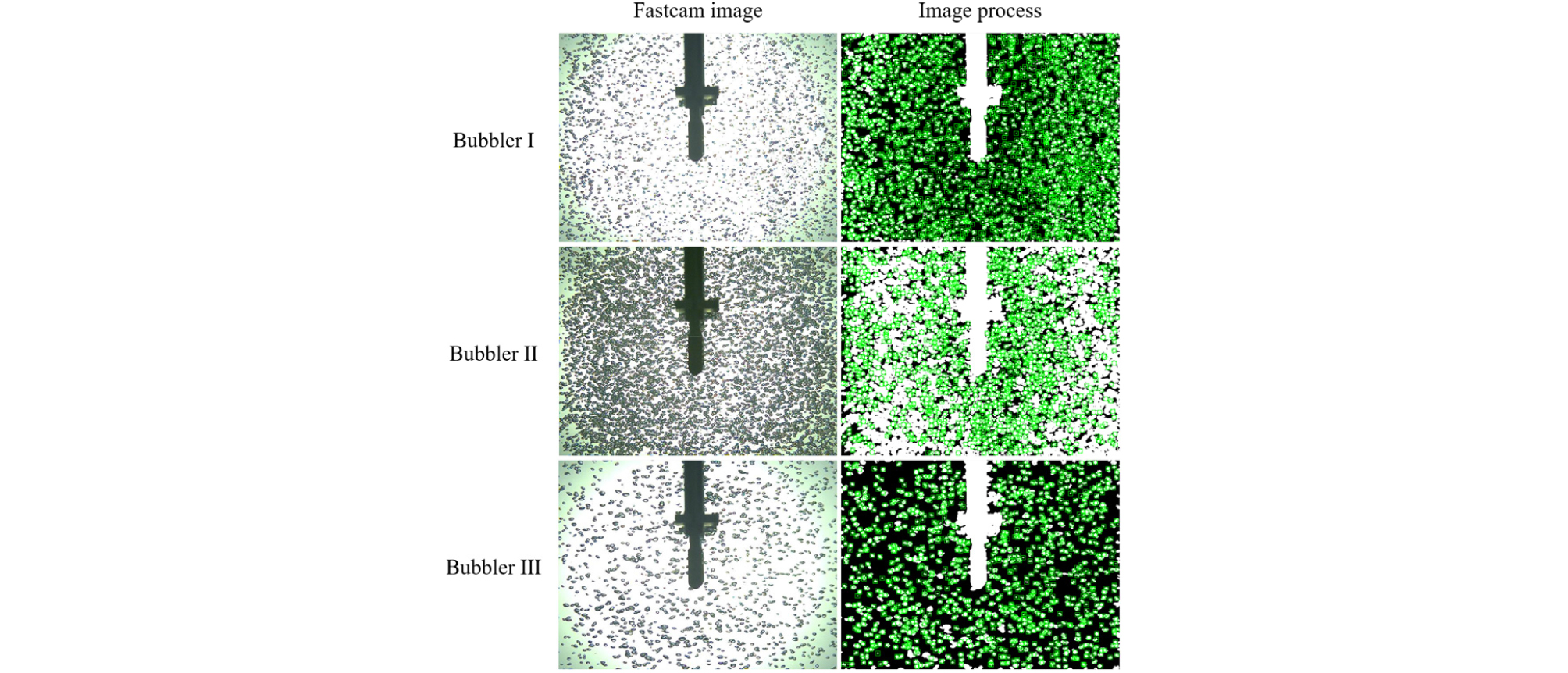
Fig. 6은 동일한 유량(Q = 10 l/min)에 대해 기포 발생기 차이에 따라 발생하는 기포 이미지와 이를 해석한 결과를 보여준다. 우선 고속 카메라 이미지에서의 기포 발생 특성을 비교해보면 Bubbler I과 Bubbler II의 경우 발생하는 기포의 크기는 유사하지만 개수 차이가 나는 것을 확인할 수 있다. 반면, Bubbler III은 Bubbler I, II에 비해 상대적으로 기포의 크기가 크고 기포의 개수가 작은 것을 알 수 있다. 고속 카메라 이미지를 해석한 결과를 보면 이러한 차이를 보다 분명히 확인할 수 있으며, Bubbler II의 경우 기포의 높은 밀도로 인해 발생하는 기포가 과도하게 겹쳐 해석이 부정확하여 본 이미지 해석 결과에서는 Bubbler I과 Bubbler III의 결과를 서로 비교하였다.

Fig. 6.

(Color available online) Comparison of bubble characteristics according to bubble generator.

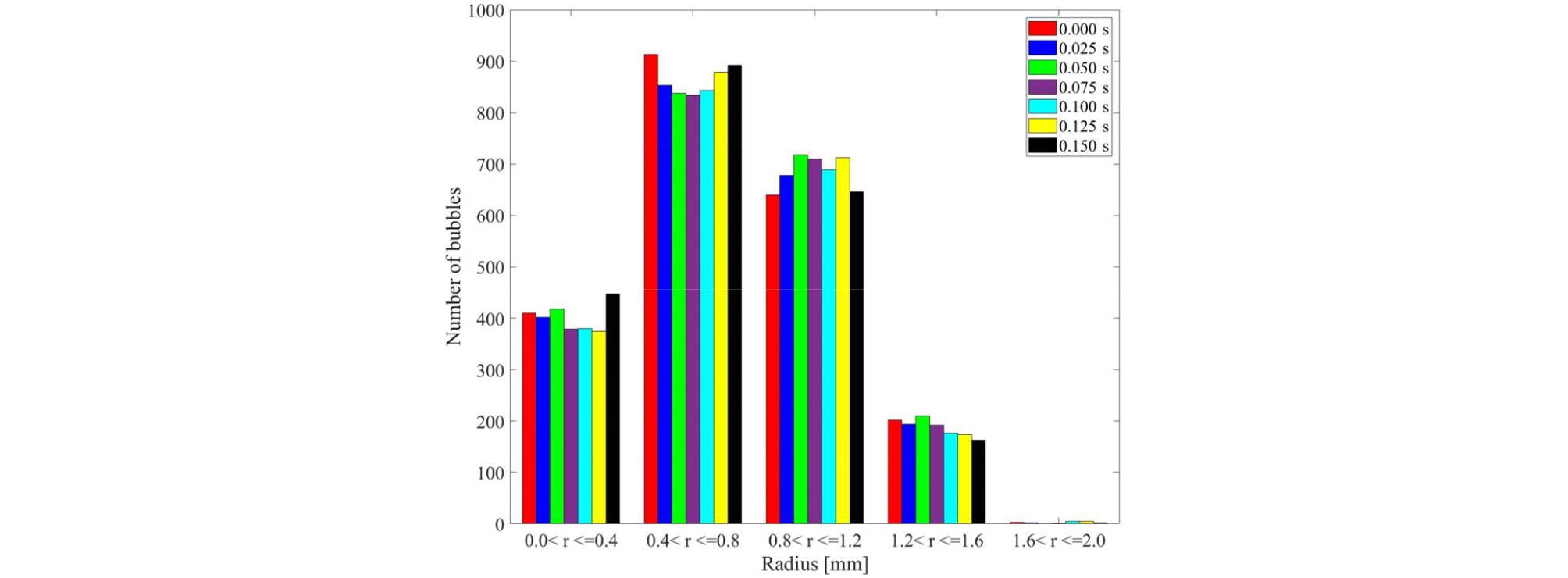
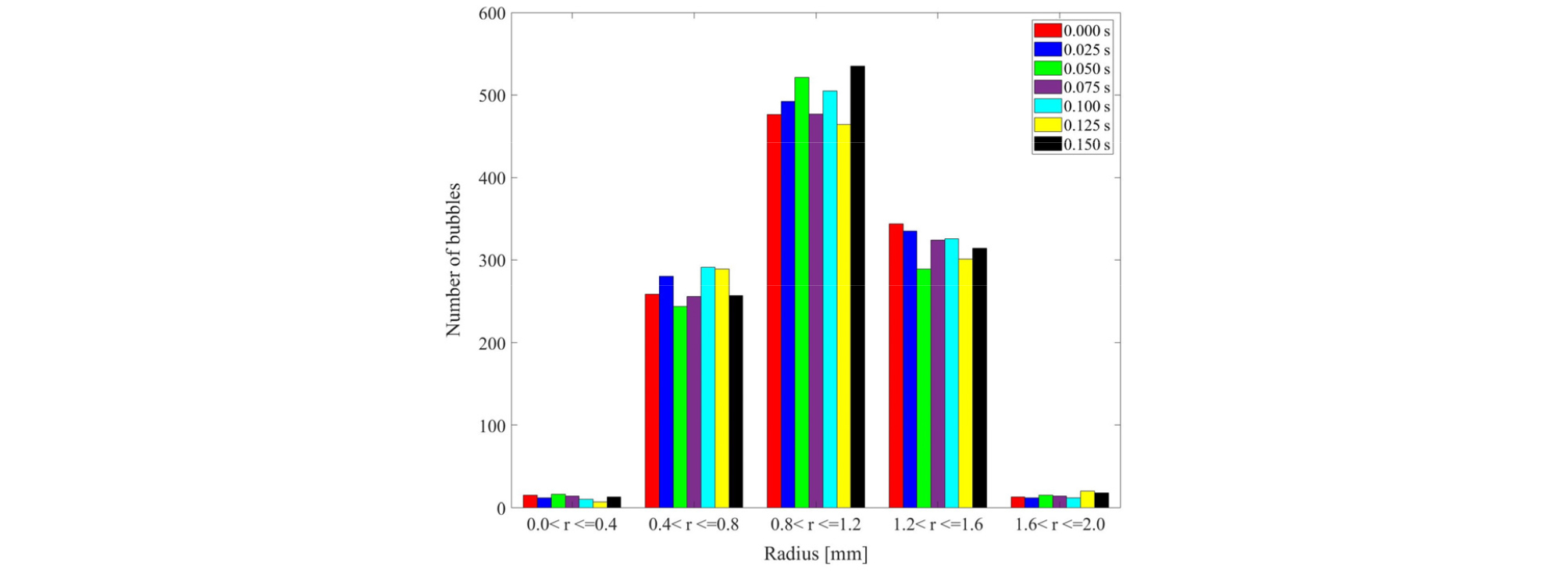
Figs. 7과 8은 Bubbler I과 Bubbler III의 이미지 해석 결과를 사용하여 발생하는 기포의 크기 분포를 해석한 결과를 보여준다. 각각의 그래프는 시간대별로 기포 크기 분포의 차이를 보여주며, 전체적인 크기 분포 경향은 시간에 따른 차이는 없는 것을 알 수 있다. 또한 해석 결과에서 Bubbler I의 경우 Bubbler III에 비해 상대적으로 크기가 작은 기포(반지름 0.4 mm이하)가 많은 것을 확인할 수 있다.

Fig. 7.

(Color available online) Distribution of bubble radius in Bubbler I according to time (Q = 10 l/min).

Fig. 8.

(Color available online) Distribution of bubble radius in Bubbler III according to time (Q = 10 l/min).

본 연구에서 수행한 2차원 영상분석을 통해 기포의 크기 분포를 추정하는 데는 한계가 있다. 2차원 분석에서는 3차원 공간에 존재하는 기포가 하나의 2차원 단면에 모두 투영되므로 기포의 개수가 과도하게 추정될 가능성이 높다. 또한 기포의 이미지 간에 겹침 현상으로 인해 기포의 크기 또한 크게 추정되었을 것이다. 이러한 단점을 극복하기 위해 최근 3차원 계측기법에 관한 연구가 수행되고 있다.^[16] 기포 음향실험과 더불어 정밀한 3차원 계측이 수행된다면 보다 의미 있는 분석이 가능할 것으로 판단된다.

4.2 음향 분석 결과

음향시험에서 계측된 데이터로부터 기포층에 의한 삽입손실 $L_b\left(f\right)$은 다음과 같이 정의하였다.

Eq. (6)에서 는 평균 연산자이며, $p_o$와 $p_b$는 기포가 없을 때와 있을 때에 계측된 압력을 나타낸다. 역산을 위한 감쇠 계수는 $\alpha \left(f\right)=L_b\left(f\right)/d_b$[dB/m]의 관계식으로 구하였다. 이 때, $d_b$는 형성된 기포층의 두께를 의미한다.

계측 데이터의 수가 제한적이므로 충분한 역산 데이터 수($N_f$)를 확보하기 위해 데이터 보간이 필요하다. 기포의 분포 범위가 넓고 해상에서의 기포의 분포는 파워법칙(power law)^[7]으로 근사될 수 있음을 고려해 기포 분포값에 로그를 취해 보간을 수행하였다. 역산에 사용된 주파수와 반지름 영역의 데이터 개수는 각각 $N_f$ = 150 그리고 $N_a$ = 75이다. 한편, Eq. (1)의 적분을 위해 반지름 영역의 데이터는 1,000개의 데이터로 선형 보간하였다.

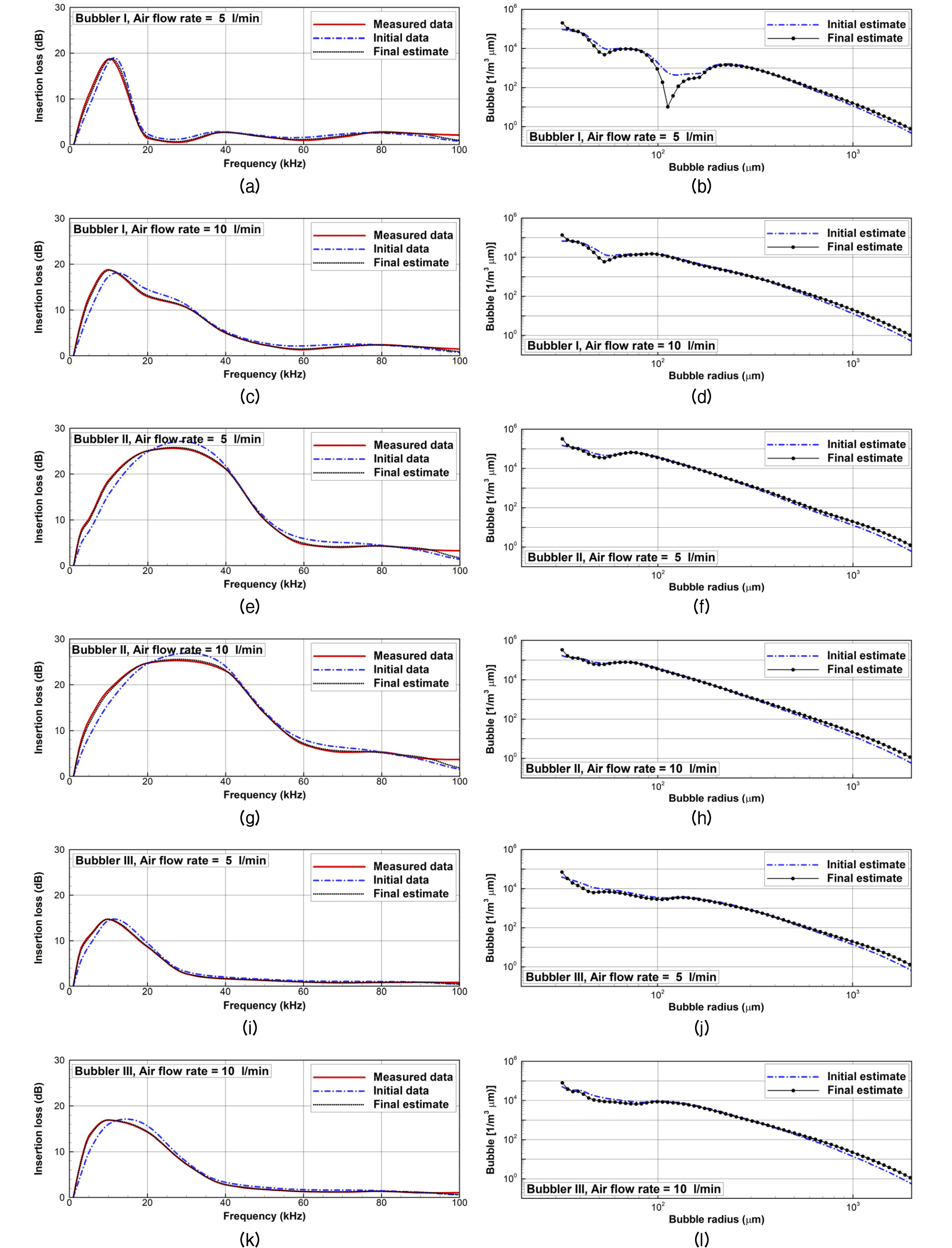
역산은 세 종류의 기포발생기에 공급된 공기의 유량(air flow rate)이 5 l/min, 10 l/min 에 대해 각각 수행되었다. Fig. 9는 음향 계측 결과와 역산결과를 보여준다. Fig. 9에서 왼편에는 보간 된 계측 삽입손실(적색 실선), 초기해에 해당하는 삽입손실(청색 일점쇄선) 그리고 최종 추정된 기포분포에 의한 삽입손실(흑색 점선)을 비교하여 나타내었다. 그림의 오른편은 공기분포의 초기 추정값(청색 점선)과 최적해(흑색 실선과 원)을 보여준다.

Fig. 9.

(Color available online) Inversion results for Bubbler I, II and III with air flow rate of 5 l/min and 10 l/min. Insertion loss are shown in the left column and estimated bubble density are given in the right column.

Table 4에는 기포 발생기의 공기 유량 별 삽입손실량과 추정 기포율(void fraction)을 수록하였다. 기포율은 단위체적 당 기포가 차지하는 부피를 말하고, 삽입손실량은 1 kHz ~ 100 kHz 범위의 전체 파워를 의미한다. 삽입손실량은 기포 발생기 II에서 가장 크고 기포 발생기 III에서 가장 작게 나타났다. 반면에 기포율은 기포 발생기 I이 가장 작다. 이러한 삽입 손실량과 기포율의 경향성 차이는 두 값이 발생된 기포의 크기 분포(결과적으로는 주파수 특성)에 따라 달라짐에 기인한다. 기포 발생기 I과 III은 입력 공기유량별 기포 발생량의 차이가 발생했다. 그런데 기포 발생기 II는 공기유량에 따른 차이가 미미한 것으로 보였고 이는 재질의 특성에 따른 것으로 판단된다.

영상분석 결과(Figs. 7과 8)와 음향 역산결과(Fig. 9)를 비교할 때, 영상분석 결과에서 작은 반지름(400 $\mu m$ 이하)의 기포 개수가 음향 역산결과에 비해 현저히 적다는 점이다. 이는 Macintyre^[17]가 지적한 바와 같이 광학적 관측은 주로 부력이 크고 빛을 잘 반사하는 기포를 탐지하며, 그렇지 못한 크기가 작은 기포는 탐지 못할 가능성이 크기 때문인 것으로 파악된다. 음향 역산결과는 기포의 크기가 작아질수록 기포의 개수는 증가하며 70 μm ~ 120 μm에서 1차 피크를 보인 후 다시 증가하는 형태를 보였다. 이는 해양에서 자연적으로 존재하는 기포 군집의 분포가 약 30 μm에서 피크를 보이며 지수적으로 감소하는 것^[7,17]과 피크의 크기는 다르나 그 경향성은 유사한 것으로 판단된다.

V. 결 론

본 연구에서는 음향 감쇠 데이터로부터 기포의 크기 분포를 추정하기 위해 제 1종 Fredholm 적분방정식으로 표현된 역산란 문제를 최적화 문제로 정의한 후 Levenberg-Marquardt 비선형 최적화 기법을 적용하였다. 제안된 기법은 두 종류의 시뮬레이션을 통해 유용함을 검증하였다. 세 종류의 기포 발생기를 이용하여 사각 수조(1.0 m × 0.54 m × 0.6 m)에서 기포 실험을 수행하였다. 고속카메라 영상분석을 통해 기포 발생기 별 기포의 분포 특성을 확인하였고, 2차원 관측법의 한계를 확인하였다. 음향 실험을 통해 주파수 별 삽입손실을 계측하였고, 이로부터 기포의 크기 분포를 역산하였다. 역산 결과 추정된 기포의 분포는 해양에서 자연적으로 분포하는 기포의 분포와 비교할 때 피크 반지름이 커졌을 뿐 분포 경향성은 유사한 것으로 판단되었다.

최적화 과정에서 역산 인자 개수($N_a$)와 목적함수의 데이터 개수($N_f$)의 결정에 신중해야 한다. 너무 많은 역산 인자는 계산시간이 길어질 뿐만 아니라 Jacobian 행렬의 조건수가 커져서 역산해의 안정성이 저하 될 수 있다. 반대로 역산 인자의 개수가 작아지면 기포의 크기 분포의 분해능이 떨어지는 단점이 있다. 본 연구에서 $N_a$는 75 ~ 100 사이가 적절한 것으로 파악되었으나 최적의 역산 인자 개수는 계측 데이터의 주파수 범위 또는 대상 반지름 범위에 따라 달라질 것이다. 한편, 목적함수의 데이터 개수는 주파수별 음향특성(감쇠)이 충분히 반영될 수 있도록 설정되어야 한다. 본 연구에서 $N_f$는 150으로 설정하였으나, 이 역시 주파수 및 대상 반지름 범위에 따라 신중히 설정되어야 할 것이다.

음향학적 기포 분포 역산에서 계측된 음향 데이터의 질은 중요한 문제이다. 본 연구에서는 사각수조의 크기로 인해 10 kHz 미만의 음향신호는 반사파에 의한 영향을 배재할 수 없다. 향후 연구에서는 수조의 크기를 키워서 보다 신뢰성 있는 저주파 영역의 데이터를 확보할 예정이다.

끝으로 본 연구에서는 이미지 분석을 통한 기포의 분포 특성과 역산된 분포와의 직접적인 비교를 수행하지 못했다. 3차원 계측법 등 추가 연구를 통해 광학 계측 결과와 음향 분석 결과와의 비교가 수행되어야 할 것으로 판단된다.

부 록

기포의 표면장력을 무시하고 기포 내부기체의 단열과정 진동을 가정할 때, 반지름이 $a$인 기포의 공진주파수($f_{r0}$)는 기체의 상태방정식과 운동량방정식으로부터 다음과 같이 유도된다.

이 때, $\gamma$는 비열비이고, ${\rho }_A$와 $P_A$는 각각 기포 외부의 유체 밀도와 정압력을 의미한다.

그런데 기포의 크기가 작아질수록 표면장력의 효과는 점점 커지게 되고, 내부기체의 진동은 등온과정에 가깝게 된다. 기포의 표면장력을 고려할 때, 기체 내부의 평균압력($P_{iA}$)은 외부 유체의 정압력($P_A$)보다 커지게 되며, 이를 보정인자 $\beta$를 도입하여 $P_{iA}=\beta P_A$로 정의한다. 또한, 기포 내부의 압력과 부피 사이의 위상을 고려하기 위해 보정인자 $b$와 $d$를 도입하여 유효 비열비를 $\gamma \text{'}=\gamma (b+id)$로 정의한다. 보정인자는 주파수 $f$의 함수로서 다음의 관계식으로 표현된다.

위 식에서 $X=a\sqrt{4\pi f{C}_{pg}{\rho }_g\left[1+2\tau /\left(P_{A}a\right)\right]/K_g}$이고, $C_{pg}$, $K_g$, 그리고 ${\rho }_g$는 각각 기포 내부기체의 정압비열, 열전도율, 그리고 해수면 높이에서 공기 중 내부기체의 밀도를 의미한다. 또한 $\tau$는 기포의 표면장력을 나타낸다. 한편, $X$의 값이 큰 경우 $\sinh \left(X\right)$와 $\cosh \left(X\right)$는 공히 발산을 하지만, $d/b$와 $b$는 각각 0.0과 1.0에 수렴함에 유의한다. 이상의 보정인자를 이용하면 수정된 공진주파수($f_r$)는 다음과 같이 정의된다.

Eq. (A.5)에서 $b$와 $\beta$는 주파수 $f$의 함수이므로 공진주파수는 비선형방정식의 해를 구해야 한다. 본 연구에서는 Matlab의 ‘fzero()’ 함수를 이용하여 해를 구하였고, 초기해는 $f_{r0}$를 적용하였다. 끝으로, 주파수 $f$에서의 기포의 댐핑상수 $\delta$는 다음과 같이 정의된다.

Eq. (A.6)의 우변의 세 항은 각각 재방사에 의한 댐핑(${\delta }_r$), 열전도에 의한 댐핑(${\delta }_t$), 그리고 유체의 전단점성($\mu$)에 의한 댐핑(${\delta }_v$)에 해당한다.

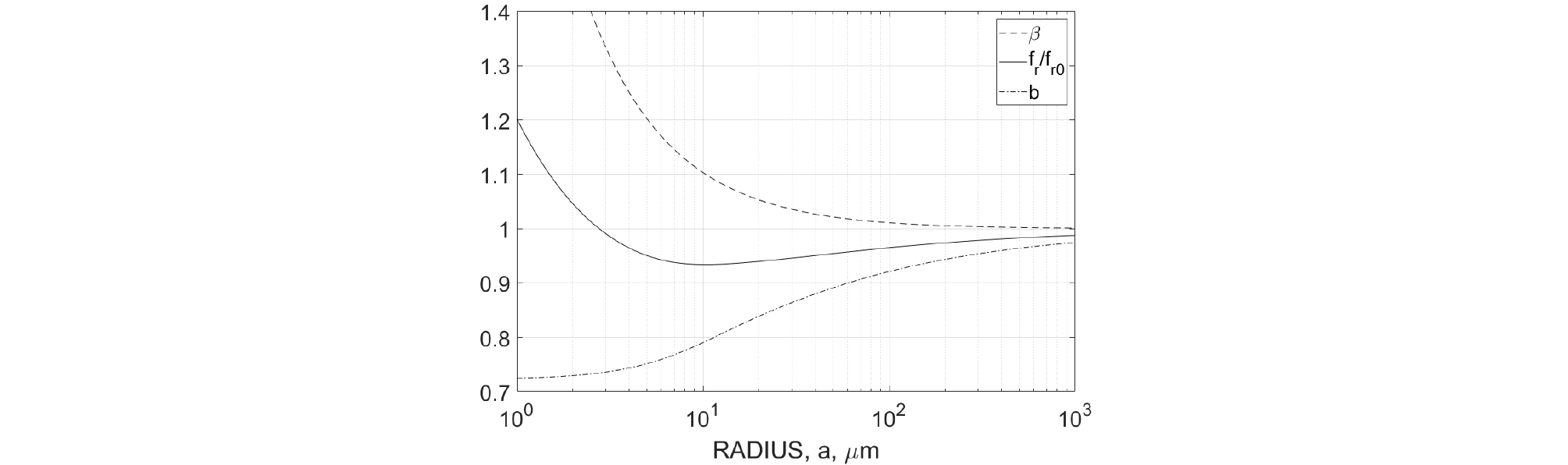
Fig. A.1은 기포의 크기에 따른 보정인자 $\beta$와 $b$, 그리고 보정 전후 공진주파수의 비를 보여준다. 그림에서 표면장력 보정인자($\beta$)는 1.0보다 큰 값을 가지며 기포의 크기가 작을수록 그 값이 커지게 된다. 반대로 비열비 보정인자($b$)는 1.0보다 작은 값을 가지며, 기포의 크기가 작을수록 그 값 또한 작아진다. 두 보정인자의 기여도에 따른 공진주파수비($f_r/f_{r0}$)의 거동에 살펴보면 기포의 크기가 작은 경우 (a < 3 μm) 표면장력 및 등온과정의 영향이 크나, 기포의 크기가 큰 경우 (a > 100 μm)에는 두 효과를 무시해도 5 % 이내의 오차에서 공진주파수를 추정할 수 있음을 알 수 있다.

Fig. A.1.

Ratio of resonance frequencies ($f_r$/$f_{r0}$) with modification constants $b$ and $\beta$ at $f=f_r$.^[1]

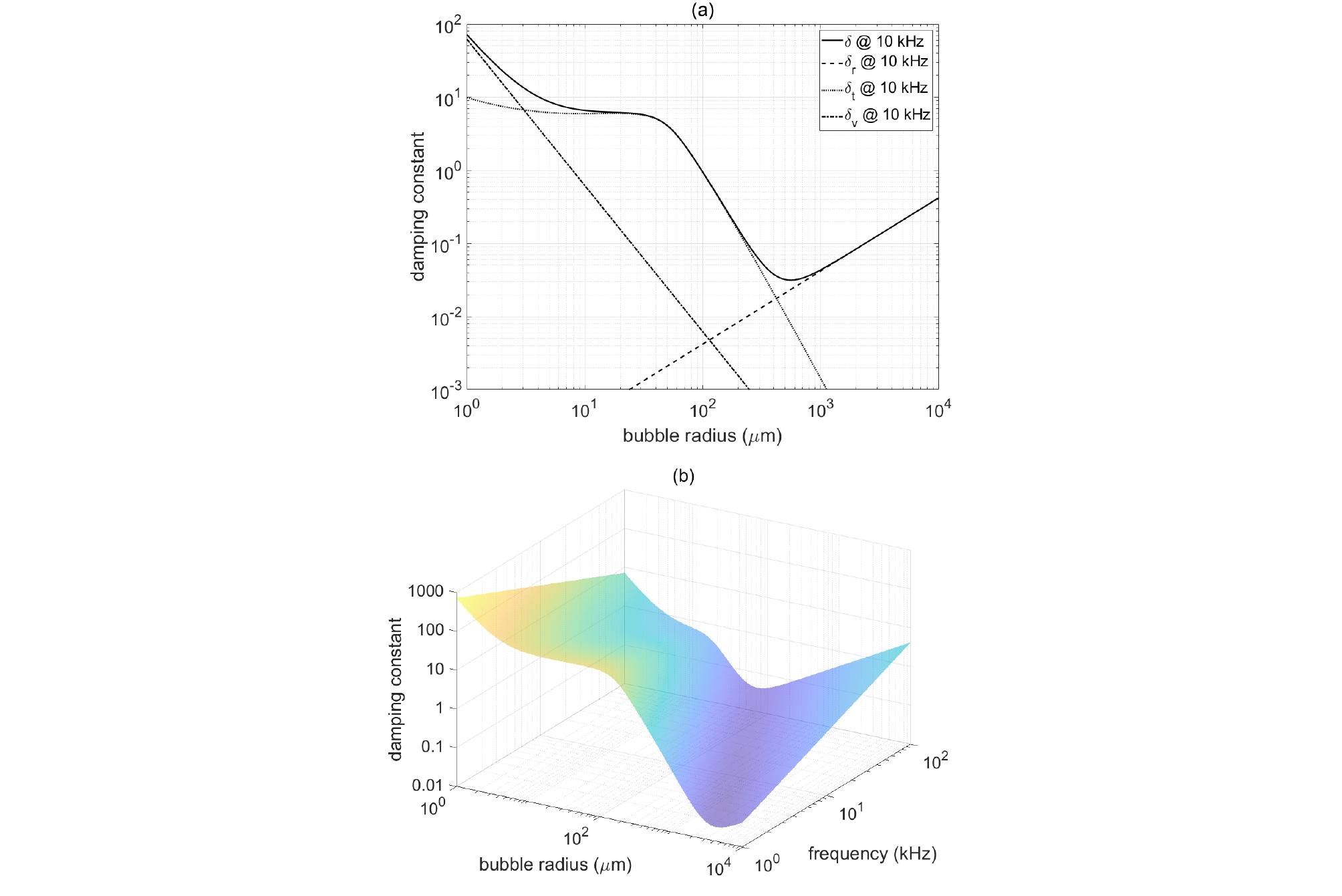
Fig. A.2(a)는 주파수 10 kHz에서 댐핑상수 $\delta$와 각 구성 성분의 거동을 보여준다. 기포가 커짐에 따라 점성(${\delta }_v$), 열전도(${\delta }_t$), 재방사(${\delta }_r$)의 순서로 댐핑의 주된 기여 성분이 바뀜을 알 수 있다. Fig. A.2(b)는 기포의 크기 및 주파수에 따른 댐핑상수의 계산결과를 보여준다. 그림에서 각 주파수에서 댐핑상수($\delta$)의 형태는 10 kHz에서와 유사하며, 최저 댐핑상수에 해당하는 반지름은 주파수가 증가할수록 작아짐을 알 수 있다.

Fig. A.2.

(Color available online) (a) Damping constants, ${\delta }_r$, ${\delta }_t$, ${\delta }_v$, and $\delta$, of air bubbles as a function of bubble radius for the frequency of 10 kHz. (b) surface plot of damping constant $\delta$ as a function of bubble radius and frequency.